Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353On-line version ISSN 2346-2183
Dyna rev.fac.nac.minas vol.79 no.172 Medellín Mar./Apr. 2012
HYDROGEN KINETICS LIMITATION OF AN AUTOTROPHIC SULPHATE REDUCTION REACTOR
LIMITACIÓN CINÉTICA DE HIDRÓGENO DE UN REACTOR AUTOTRÓFICO DE REDUCCIÓN DE SULFATO
CÉSAR SÁEZ-NAVARRETE
Ph.D. Pontificia Universidad Católica de Chile, csaez@ing.puc.cl
LEONARDO RODRÍGUEZ-CÓRDOVA
Ph.D. (c), Profesor, Pontificia Universidad Católica de Chile, Universidad Mayor, larodrig@ing.puc.cl
XAVIER BARAZA
Dr., Ing. Químico. Universidad Oberta de Catalunya, jbaraza@uoc.edu
CLAUDIO GELMI
Ph.D. Pontificia Universidad Católica de Chile, cgelmi@ing.puc.cl
LEANDRO HERRERA
Ph.D. Profesor, Universidad Mayor, leandro.herrera@gmail.com
Received for review July 5th, 2011, accepted January 23th, 2012, final version February, 12th, 2012
ABSTRACT: Sulphate-reducing bacteria (SRB) are microorganisms that can be used as removal agents in polluted water sources. The use of inorganic substrates in SRB systems could reduce the cost and simplify operation. However, the use of H2 as an energetic substrate and the production of H2S as a metabolic product could produce kinetic limitations. The aim of this study was to assess the extent to which the kinetics of a sulphate reduction bioreactor was limited by its gas transfer capacity. Reactor kinetics were monitored by total pressure kinetics without sulphate limitation. It was concluded that the bioreactor design should be based on transfer properties. The uptake rate of H2 reached a maximum of 10-4 M/min, equivalent to a sulphate reduction rate of 3.4 g·L-1·d-1. The hydrogen mass transfer rate required a kLa of 1.48 min-1 at 1.2·109 cells/L in order to avoid limitation by H2 bio-availability (1.23·10-9 L·min-1·cell-1), which is a relevant value for scaling-up purposes.
KEYWORDS: Sulphate reducing bacteria, hydrogen, mass transfer, autotrophic.
RESUMEN: El uso de sustratos inorgánicos podría reducir los costos y simplificar la operación de sistemas de tratamiento de aguas que utilizan bacterias reductoras de sulfato. Sin embargo, el uso de H2 como sustrato energético y la bioproducción de H2S podrían provocar limitaciones cinéticas. El objetivo de este estudio fue evaluar las condiciones en las que la capacidad de transferencia de masa de un bioreactor de reducción de sulfato, limita su cinética de reducción. La cinética del reactor fue obtenida monitoreando la presión del sistema en condiciones de no limitación por sulfato. Se concluyó que el diseño del bioreactor debería basarse en sus propiedades de transferencia. La tasa de consumo de H2 alcanzó un máximo de 10-4 M/min, para una tasa de reducción de sulfato de 3.4 g·L-1·d-1. Para evitar limitación por H2 se requirió un kLa de 1.48 min-1 a 1.2·109 cells/L (1.23·10-9 L·min-1·cell-1), valor relevante para propósitos de escalamiento.
PALABRAS CLAVE: Bacterias reductoras de sulfato, hidrógeno, transferencia de masa, autotrófico
1. INTRODUCTION
Water pollution by sulphates is common in areas with mineral deposits. Sulphate-reducing bacteria (SRB) are anaerobic microorganisms that employ sulphate as a terminal electron acceptor for producing hydrogen sulphide. Sulphate-reducing bacteria can grow heterotrophically or autotrophically, using H2 as the electron donor and CO2 as the carbon source [1-4]. In nature, SRB are commonly found in marine sediments, volcanic ecosystems, in the rumen of a number of mammalian species, as well as some geothermal waters. Some groups are also found in sulfur-contaminated wastewater.
The biological reduction of sulphate produces hydrogen sulphide (H2S), which is used for separating heavy metals in liquid residues, precipitated as sulphides [5-8]. Other applications include the production of commercially-viable molecules (e.g., NaHS) and the recovery of many metals [9-11]. Sulphate-reducing bacteria metabolism results in alkalinity that can be used to neutralize acidic treatment flows [5,12].
The reduction of sulfuric acid, as verified in autotrophic, lithotrophic bacteria, follows the stoichiometry [13-15]

The biological processes for sulphate reduction in aqueous systems are based on the biological activity of SRB, but bioreactor design is still a field of research in which many questions remain open. One such question is related to the limiting species and its impact on reduction kinetics, given the particular bacterium selected for the process. For example, a bioreactor designed for the reduction of sulphate should be studied and designed assuming that sulphate is the limiting substrate; an assumption that can only be valid in heterotrophic bioreactors. For autotrophic bioreactors, many authors have pointed out [15-17] that the bio-availability of aqueous hydrogen limits the reaction rate. The bioreactor used in this work was completely sealed and, in contrast to most experimental studies, the gas phase was permanently recycled to quantify hydrogen consumption. We believe that a closed system would provide a more realistic basis for scaling-up, on account of the cost of venting hydrogen in a large-scale system. Furthermore, we were interested in finding the operational variables that could ensure that the reaction was not limited by any substrate.
As shown in (1), two gases dissolved in the aqueous phase participate in this reaction: the supply of hydrogen (H2), and the reaction product, hydrogen sulfide (H2S). As these bacteria are autotrophic, carbon dioxide (CO2) also must be present, which is incorporated by the bacteria as bicarbonate.
Since this process uses gases to treat and to produce inorganic products, it offers several advantages. First, compared to the use of heterotrophic bacteria, no organic compounds need to be added and so no downstream polishing is needed prior to water reuse or environmental discharge. Secondly, the process requirements (H2 and CO2) and the process product (H2S) are gases adsorbed in the aqueous phase, so that their recovery will only require desorption, rather than other more complex and costly separation processes.
The advantages offered by gases, impose certain challenges at the same time: gases would have to be transferred to the aqueous phase at such a rate that their dissolved concentrations do not limit the kinetics of the process. Two such limiting mechanisms can be identified: (i) hydrogen gas transfer to the aqueous phase, because it is scarcely soluble; and (ii) hydrogen sulfide transfer from the aqueous phase [18], because it is a soluble gas and could inhibit cell growth [19].
The increased bio-availability of aqueous hydrogen would increase the rate of production of hydrogen sulfide; therefore increasing the likelihood of inhibition. A strategy should be applied so that both requirements are simultaneously met: high aqueous hydrogen concentration and low aqueous hydrogen sulfide concentration. As far as we know, there are no parameters published for designing the operation of this application. Although the scaling criteria using transfer properties might be clear, further work is still needed to establish the particular rate of transfer required, as well as the consumption rate of both hydrogen and sulphate.
Gas-liquid mass transfer properties
In this paper, it was assumed that gas-liquid mass transfer followed the classical theory [20] in which the hydrogen transfer rate is proportional to a driving force and the proportionality constant depends on the liquid and gas properties and the interface area (2). Due to the low solubility of hydrogen, it was assumed that solubility followed Henry's law. Therefore, the equilibrium value was given by the constant, KH times the gas partial pressure, [H2]gas. As usual, kLa, was used as a function of the gas flow rate, in order to reflect the transfer properties at any given operation point. Thus, kLa was varied by changing the gas flow rate, which changes the interfacial area and the volumetric mass transfer rate, f, was:

The consumption of hydrogen is related to the biomass density, X. If a Monod type kinetic expression is used for the specific growth rate, the kinetics of the aqueous hydrogen as a limiting substrate could be understood as shown in (3), where the volumetric flow of the liquid is QL, with a maximum uptake velocity mmax; a half saturation constant KM, and an inhibition constant KI (to account for the eventual inhibition due to the product, which is hydrogen sulfide, reported to be inhibitory in both of its aqueous forms [H2S]aq and [HS-]):

From (3), it is clear that a simple method for increasing the bio-availability of [H2]aq would be to operate at a high partial pressure of [H2]g which would increase the driving force for its transfer. The increase of [H2]g pressure could be achieved by elevating the reactor operating pressure, so that it might be an operationally simple requirement. The obvious second alternative would be to operate at a high interface area, as this would increase the global mass transfer coefficient. Only the second alternative could satisfy the design requirements, because the first would increase the inhibition by [H2S]aq at the same time that the [H2]aq was increased [18]. On the contrary, the increase in the global mass transfer rate coefficient would also help to decrease the inhibition through increased transfer of [H2S]aq from the aqueous to the gas phase (4).

In this case, the increase in gas flow would increase the transfer of [H2S]aq from the aqueous phase because that gas phase is far from the saturation value ([H2S]g is to be kept as low as possible in the experimental system).
The detailed, quantitative understanding of the transfer phenomena in this bioreactor will help in the correct design, which would eventually imply changing the reactor design altogether, from a CSTR to a gas-lift, for example [21-22]. The design should attain a transfer rate that is high enough for the kinetics not to be limited by the bioavailability of aqueous hydrogen but, simultaneously, hydrogen sulfide should be kept below its inhibition threshold [19,23-25].
In order to find the rate of transfer required by the operation, it would be necessary to determine the rate at which kinetics are not any longer limited by transfer phenomena. In particular, in this research, a well characterized continuous stirred reactor was used to observe the dynamic response when the gas flow rate through it was changed to known values.
2. EXPERIMENTS
2.1. Materials and methods
A two phases, aseptic (non-sterile), continuous stirred glass bioreactor was set up to develop a culture of SRB (see Fig. 1). The biomass Desulfovibrio desulfuricans (NCIMB 8372) was obtained from previous experiments in batch systems. Prior to these experiments, the bioreactor was operated during 3 months under a gas flow rate through the reactor of around 0.6 L/min.

Figure 1. Experimental reactor and equipment. PC and PMC pump controllers; TC temperature controller; VC solenoid valve controller; T temperature transmitter; pH transmitter; P pressure transmitter; A/D analog to digital (and vice-versa) converter. The heavy line shows that the gas line was completely closed
The bioreactor volume was 1.6 L and the liquid phase was 1.3 L. Due to gas pipes and gas washing bottles, the total gas volume of the experimental system changed from one experiment to the other and was measured each time. The gas volume ranged from 0.5 to 1.2 L. A 4-cm magnetic bar, at 270 RPM stirred the bioreactor.
The bioreactor temperature was automatically controlled at 30±1 °C. The bioreactor was fed with 2 parts of 0.4 M sulfuric acid and 1 part growth medium in volume, as needed to control pH between 6.95 and 7.05. The sterile non-specific growth medium had a similar composition to the one given previously by Postgate [26], but modified so that no sulphate was incorporated: 0.5 g/L of K2HPO4; 1 g/L of NH4Cl; 0.1 g/L of CaCl2x2H2O; 0.1 g/L of C2H3NaO2S (sodium thioglicolate); and 0.1 g/L of C6H7NaO6 (sodium ascorbate). The hydrogen gas was fed from a commercial cylinder to keep total pressure at the desired value. The gas cylinder contained a 95% v/v hydrogen and 5% v/v carbon dioxide certified mixture.
As shown in Fig. 1, the gas flow through the reactor was permanently recycled and washed by a series of copper sulphate 250 mL washing bottles (except for three experiments where gas flow was null). The copper sulphate reacted with the hydrogen sulfide of the gas line to form insoluble copper sulfide, so that hydrogen sulfide was low enough. The aqueous forms, [HS-] and [H2S]aq, were below 0.1 mM (experimental measurement). The traps had a solution of 7 g/L copper sulphate, brought to pH 7 with sodium hydroxide.
The bioreactor instrumentation consisted of a thermocouple (K type), a pressure transducer (Vetto) and indicator, electrodes for pH and Eh (Hanna Instruments); an electric heater (custom-made); a relay for the gas feed; and a control for the liquid input pump based on an OPTO 22 control and data acquisition system. The set point of the gas recycling pumps (CVB) was set for each experiment and the speed was then sustained by an automatic RPM control, as indicated in Fig. 1.
A computer was used to register and control total pressure in the reactor, which was normally kept at 2 psig by briefly opening a solenoid control valve to restore the pressure from the gas cylinder since the hydrogen and the carbon dioxide were consumed by the bacteria. The pH was also controlled by automatically feeding a mixture of 0.4 M sulfuric acid and growth medium, as mentioned previously. The temperature was controlled by an independent PLC system and the Eh was continuously monitored to verify the reductive conditions in the system (see Fig. 1).
During the kinetic experiments, the pressure controller was in stand-by mode; the pressure was allowed to fall, and pressure kinetics was recorded for later off-line analysis. In fact, total pressure kinetics reflects hydrogen partial pressure kinetics in a condition where the transfer rate is reduced because the transfer area was reduced to the surface of the liquid.
The gas-liquid mass transfer properties of the reactor were determined for oxygen using growth medium and changing air flow rate. The transfer properties for hydrogen were then calculated using the diffusion coefficients [27].

The experimental design consisted of setting the total gas pressure at 2 psig and then recording the falling pressure as hydrogen was consumed. The gas phase of the reactor was composed of hydrogen [H2]g, hydrogen sulfide [H2S]g, carbon dioxide [CO2]g, and water vapor [H2O]vap. The total pressure, PT, was calculated as the sum of all the partial pressures.
It was assumed that the hydrogen sulfide partial pressure was negligible, on account of the high efficiency of the gas washing system. In addition, the vapor pressure of water was assumed to be constant at its equilibrium value (PH2O = 31.8 mm Hg at 30 °C), and the ratio of the partial pressures of hydrogen and carbon dioxide remained at its feed value, 95/5. Therefore, the consumption of hydrogen was obtained from the fall of total pressure according to:
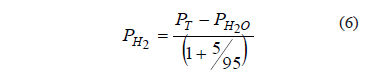
The hydrogen partial pressure, PH2, was used to obtain its molar concentration according to the ideal gas law.
Pressure measurements (PT) were used to calculate the consumption of hydrogen gas, according to (5) and were expressed as molar concentration. The consumption rate of hydrogen was expressed in micromoles of hydrogen per liter of gas.
2.2. Results and discussion
The experimental determination of the transfer properties of this reactor resulted in a typical exponential relationship between the transfer coefficient and the volumetric gas flow rate, given by the equation:

where a = 0.223 min-1; b = 1.808 min-1; and c = 0.381 min·mL-1.
Figure 2 shows the relationship between the gas flow rate (expressed as volumetric flow rate) and the consumption of hydrogen. The figure shows that when the reactor was operated without gas recycling (zero flow rate), but mechanical agitation was maintained, the hydrogen consumption was the lowest, and mass was transferred only at the surface of the reacting liquid. Additionally, when the gas flow rate was increased, it was no surprise to observe that the consumption rate followed the same trend, following a typical saturation curve. The continuous line drawn between the data points in the figure was a simple exponential adjustment, only indicating the main value tendency of the kinetics. The saturation profile (Fig. 2) might be explained by postulating that the reactor reached a point where the increment in gas flow rate would not increase the transfer rate, on account of the bubble regime change, from bubbles to slugs but this was not seen to occur in this bioreactor. Consequently, a scaling parameter for this reactor would be the mass transfer rate rather than the flow rate.

Figure 2. Hydrogen uptake rate as a function of gas flow rate
Figure 3 shows a similar trend as Fig. 2, but hydrogen gas consumption rate was plotted in Fig. 3 as a function of the mass transfer rate. This was done in order to highlight that a threshold exists in which the hydrogen availability was not limiting any longer. It is common for a reacting system to become limited by a second substrate when the original limiting substrate is brought to an excessive level. For example, sulphate instead of hydrogen might become limiting. Therefore, the sulphate concentration was also manipulated to show that it was not limiting at any point along the experiment. In order to ensure this, the first four experimental points were obtained by operating the bioreactor at a rather low sulphate concentration; while the following points were measured at a high sulphate concentration. Also, cell concentration increased with the mass transfer rate, while it remained constant when sulphate was increased. Given that the increase in biomass was not significant, it was possible to estimate the uptake rate per cell at around 8·10-14 moles of hydrogen gas per cell per minute.

Figure 3. Hydrogen uptake rate as a function of the global hydrogen mass transfer coefficient
From the point of view of bioreactor scaling, an empirical rate coefficient could be proposed. This coefficient related transfer requirements and cell density at a chosen operating point. Such a coefficient was determined as the ratio of the necessary mass transfer coefficient per cell of 1.23·10-9 L·min-1·cell-1.
3. CONCLUSIONS
An autotrophic bioreactor, limited by the bio-availability of aqueous hydrogen gas, which in turn depended on the mass transfer properties of the bioreactor, was operated at diverse transfer rates, within the range of 0.2 to 1.5 min-1.
Once the gas transfer rate was high enough to show no limitation, subsequent behavior was not limited by either the energy substrate (molecular hydrogen) or the respiratory substrate (sulphate).
In this research it was found that for a given cell density, after a certain limit was reached for the bio-availability of hydrogen, a significant effect on reactor kinetics was observed. Therefore, the reactor was limited by the cell kinetics and not by external substrates. It is possible that a different reactor design would attain a different maximum level if operated at a different cell density. In this sense, a better scaling recommendation might be to use the global mass transfer rate per unit of biomass [28].
The maximum consumption rate observed was 97·10-6 moles H2/min. If this rate were used to estimate sulphate reduction kinetics, according to (1), a rate of approximately 24 micromoles sulphate per minute would be obtained. This value is equivalent to 3.46 g·L-1·d-1, a high rate for this type of bioreactor that can only be attained if gas transfer properties are not limiting. Much higher sulphate reaction rates (almost one order of magnitude higher) has been reported using gas-lift reactors and higher biomass densities [16]. Unfortunately, it is not common for authors to publish the transfer rate at which they have worked.
For a given cell density of 1.2·109 cells·L-1, the bioreactor ceased to be limited by hydrogen when it was operated at a kLa of approximately 1.48 min-1. Furthermore, the specific rate of consumption of dissolved hydrogen gas was approximately 8·10-14 moles of hydrogen gas, per cell per minute. With reference to the per unit biomass sense discussed above, the bioreactor designer should consider its operation at a transfer rate of 1.23·10-9 L·min-1·cell-1, although we do not have enough data to comment on the non-linearity of this relationship with cell density. This parameter might also prove to be useful for bioreactor design.
4. ACKNOWLEDGEMENTS
This research was supported partially by the National Commission for Scientific and Technological Research (Comisión Nacional de Investigación Científica y Tecnológica, CONICYT) of the Chilean Government via a doctoral scholarship awarded to Leonardo Rodríguez-Córdova (No. 21090472), and by CODELCO Chile. The authors also wish to acknowledge Loreto Bravo and José Hernández, University of Chile, for valuable contributions.
REFERENCES
[1] Nagpal, S., Chuichulcherm, S., Livingston, A. and Peeva, L., Ethanol utilization by sulfate-reducing bacteria: An experimental and modeling study, Biotechnology and Bioengineering, 70(5), pp. 533-543, 2000. [ Links ]
[2] Kolmert, Å. and Johnson, D.B., Remediation of acidic waste waters using immobilized, acidophilic sulfate reducing bacteria, Journal of Chemical Technology & Biotechnology, 76(8), pp. 836-843, 2001. [ Links ]
[3] Moosa, S., Nemati, M. and Harrison, S.T.L., A kinetic study on anaerobic reduction of sulphate, part II: incorporation of temperature effects in the kinetic model, Chemical Engineering Science, 60(13), pp. 3517-3524, 2005. [ Links ]
[4] Sáez-Navarrete, C., Zamorano, A., Ferrada, C. and Rodriguez, L., Sulphate reduction and biomass growth rates for Desulfobacterium autotrophicum in yeast extract - Supplemented media at 38 degrees C, Desalination, 248(1-3), pp. 377-383, 2009. [ Links ]
[5] García, C., Moreno, D., Ballester, A., Blazquez, M. and Gonzalez, F., Bioremediation of an industrial acid mine water by metal-tolerant sulphate-reducing bacteria, Minerals Engineering, 14(9), pp. 997-1008, 2001. [ Links ]
[6] Jong, T. and Parry, D.L., Removal of sulfate and heavy metals by sulfate reducing bacteria in short-term bench scale upflow anaerobic packed bed reactor runs, Water Research, 37(14), pp. 3379-3389, 2003. [ Links ]
[7] Luptakova, A. and Kusnierova, M., Bioremediation of acid mine drainage contaminated by SRB, Hydrometallurgy, 77(1-2), pp. 97-102, 2005. [ Links ]
[8] Chockalingam, E. and Subramanian, S., Utility of Eucalyptus tereticornis (Smith) bark and Desulfotomaculum nigrificans for the remediation of acid mine drainage, Bioresource Technology, 100(2), pp. 615-621, 2009. [ Links ]
[9] Santos, S., Machado, R., Correia, M. and Carvalho, J., Treatment of acid mining waters, Minerals Engineering, 17(2), pp. 225-232, 2004. [ Links ]
[10] Tabak, H.H., Scharp, R., Burckle, J., Kawahara, F. and Govind, R., Advances in biotreatment of acid mine drainage and biorecovery of metals: 1. Metal precipitation for recovery and recycle, Biodegradation, 14(6), pp. 423-436, 2003. [ Links ]
[11] Veeken, A.H.M. and Rulkens, W.H., Innovative developments in the selective removal and reuse of heavy metals from wastewaters, Water Science and Technology, 47(10), pp. 9-16, 2003. [ Links ]
[12] Lyew, D. and Sheppard, J., Use of conductivity to monitor the treatment of acid mine drainage by sulphate-reducing bacteria, Water Research, 35(8), pp. 2081-2086, 2001. [ Links ]
[13] Sorensen, J., Christensen, D. and Jorgensen, B.B., Volatile fatty acids and hydrogen as substrates for sulfate-reducing bacteria in anaerobic marine sediment, Applied and Environmental Microbiology, 42(1), 5P, 1981. [ Links ]
[14] Herrera, L., Duarte, S. and Hernández, J., Sulfate elimination to improve water quality of mine process effluents. I. Sequencing batch bioreactor growth kinetics of Desulfovibrio desulfuricans, Environmental Toxicology and Water Quality, 8(3), pp. 279-289, 1993. [ Links ]
[15] Van Houten, R.T., Yun, S.Y. and Lettinga, G., Thermophilic sulphate and sulphite reduction in lab scale gas lift reactors using H2 and CO2 as energy and carbon source, Biotechnology and Bioengineering, 55(5), pp. 807-814, 1997. [ Links ]
[16] Van Houten, R.T., Pol, L.W.H. and Lettinga, G., Biological sulfate reduction using gas-lift reactors fed with hydrogen and carbon-dioxide as energy and carbon source, Biotechnology and Bioengineering, 44(5), pp. 586-594, 1994. [ Links ]
[17] Herrera, L., Hernandez, J., Bravo, L., Romo, L. and Vera, L., Biological process for sulfate and metals abatement from mine effluents, Environmental Toxicology and Water Quality, 12(2) pp. 101-107, 1997. [ Links ]
[18] Herrera, L., Hernández, J. and Duarte, S., Sulfate elimination to improve water quality of mine process effluents. II. Hydrogen sulfide transport in biological reactors, Environmental Toxicology and Water Quality,. 8(4), pp. 409-424, 1993 [ Links ]
[19] Okabe, S., Nielsen, P. and Charcklis, W., Factors affecting microbial sulfate reduction by Desulfovibrio desulfuricans in continuous culture: limiting nutrients and sulfide concentration, Biotechnology and Bioengineering, 40(6), pp. 725-734, 1992. [ Links ]
[20] Miller, D., Interfacial area, bubble coalescence and mass transfer in bubble column reactors, AIChE Journal, 29(2), pp. 312-319, 1983. [ Links ]
[21] Heijnen, J. and Van't Riet, K., Mass transfer, mixing and heat transfer phenomena in low viscosity bubble column reactors, The Chemical Engineering Journal, 28(2) pp. B21-B42, 1984. [ Links ]
[22] Moo-Young, M. and Blanch, H., Design of biochemical reactors mass transfer criteria for simple and complex systems, Reactors and Reactions, pp. 1-69, 1981. [ Links ]
[23] Foucher, S., Battaglia-Brunet, F., Ignatiadis, I. and Morin, D., Treatment by sulfate-reducing bacteria of Chessy acid-mine drainage and metals recovery. Chemical Engineering Science, 2001. 56(4), pp. 1639-1645. 2001. [ Links ]
[24] Escobar, C., Bravo, L., Hernandez, J. and Herrera, L., Hydrogen sulfide production from elemental sulfur by Desulfovibrio desulfuricans in an anaerobic bioreactor, Biotechnology and Bioengineering, 98(3), pp. 569-577, 2007. [ Links ]
[25] Okabe, S., Nielsen, P., Jones, W. and Characklis, W., Sulfide product inhibition of Desulfovibrio desulfuricans in batch and continuous cultures, Water Research, 29(2), pp. 571-578, 1995. [ Links ]
[26] Postgate, J.R., The sulphate-reducing bacteria, Cambridge University Press, Cambridge, 1979. [ Links ]
[27] Sáez-Navarrete, C., Modelación dinámica fenomenológica de un bio-reactor continuo de reducción de sulfato [PhD Thesis]. Santiago, Chile: Universidad de Chile, 2001. [ Links ]
[28] Zapata, D., Ossa, D. and Marquez, M., Mineralogical characterization of oxidation productos in a pyrite-sphalerite system using indigenous Fe oxidizing bacteria, DYNA Colombia, 75(154), pp. 59-64, 2008. [ Links ]














