Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.80 no.179 Medellín May/June 2013
OPTIMIZACIÓN POR SIMULACIÓN BASADO EN EPSO PARA EL PROBLEMA DE RUTEO DE VEHÍCULOS CON DEMANDAS ESTOCÁSTICAS
A SIMULATION-OPTIMIZATION APPROACH BASED ON EPSO FOR THE VEHICLE ROUTING PROBLEM WITH STOCHASTIC DEMANDS
SILVIA GALVÁN
M.Sc en Ing, Industrial, Profesora Universidad Industrial de Santander, Colombia, silvia.galvan@correo.uis.edu.co
JAVIER ARIAS
Ma, Profesor Universidad Industrial de Santander, Colombia, jearias@uis.edu.co
HENRY LAMOS
Ph.D. en Matemáticas, Profesor Universidad Industrial de Santander, Colombia, hlamos@uis.edu.co
Recibido Diciembre 2 de 2012, aceptado Abril 19 de 2013, versión final Mayo 5 de 2013.
RESUMEN: En este artículo se presenta el framework SIM-EPSO para la solución del Problema de Ruteo de Vehículos con Demandas Estocásticas (VRPSD) con descarga preventiva para el caso de un solo vehículo, desarrollando la metaheurística híbrida Optimización de Enjambre de Partículas Evolutivo (EPSO) y Simulación Monte Carlo para la evaluación de la función objetivo. Adicionalmente, se usó un diseño experimental con el propósito de determinar el impacto de los parámetros del VRPSD sobre la función objetivo, y se construyó un banco de pruebas con el objetivo de medir la calidad de las soluciones encontradas en el SIM-EPSO, las cuales fueron contrastadas con la versión básica de la metaheurística Optimización de Enjambre de Partículas (PSO). Los resultados computacionales obtenidos evidencian la eficiencia del framework propuesto para encontrar mejores soluciones respecto al PSO en un tiempo computacional competitivo.
PALABRAS CLAVE: VRPSD, PSO Evolutivo, Simulación Monte Carlo.
ABSTRACT: This paper presents the framework SIM-EPSO for solving the Single Vehicle Routing Problem with Stochastic Demands (VRPSD) with preventive restocking, developing the hybrid metaheuristic Evolutionary Particle Swarm Optimization (EPSO) and Monte Carlo simulation for computing the objective function. In addition, an experimental design was used with the purpose of determining the impact of the VRPSD parameters on the objective function. Moreover, we constructed a test bed in order to measure the quality of the solutions found in the SIM-EPSO, which they were contrasted with the basic version of the metaheuristic PSO. The computational results obtained show the efficiency of the proposed framework to find better solutions regarding the PSO in a computational time competitive.
KEYWORDS: VRPSD, Evolutionary PSO, Monte Carlo Simulation.
1. INTRODUCCIÓN
El diseño de rutas vehiculares es una de las funciones más críticas dentro del sistema de transporte terrestre enmarcado en la optimización de la cadena de abastecimiento [1]. Tradicionalmente, las decisiones de distribución en el transporte terrestre se han abordado considerando los parámetros del modelo de manera determinista; como el costo, la demanda de los clientes, los tiempos de entrega, los tiempos de viaje de los vehículos, entre otros. Sin embargo, cuando se desean abordar situaciones prácticas, al problema de ruteo de vehículos se le incorporan elementos más flexibles que respondan al ambiente dinámico y complejo de los sistemas de transporte actuales, considerando entonces el diseño de rutas bajo incertidumbre de algunos o de todos los parámetros. El problema de ruteo de vehículos con uno o más parámetros estocásticos se denota como el Problema de Ruteo de Vehículos Estocásticos (SVRP). El presente trabajo se ocupa de una las variantes del SVRP, en la cual se considera incertidumbre en las demandas de los clientes. Esta variante se conoce como el Problema de Ruteo de Vehículos con Demandas Estocásticas (VRPSD).
El VRPSD surge debido a situaciones reales de entrega o de recolección de mercancías en las cuales la empresa encargada de la distribución cuenta con clientes con demandas inciertas. Bajo esta consideración, la demanda sólo será revelada en el momento en que el vehículo visita al cliente. En el caso determinista, las rutas se planean de forma que los vehículos tengan suficiente capacidad para satisfacer las demandas de los clientes dadas unas rutas preestablecidas. En el caso que las demandas son estocásticas, el concepto de "rutas preestablecidas" tiene una interpretación diferente y se requieren de reglas de decisión o políticas de ruteo que reinterpretan el concepto anterior [2].
En la literatura se han estudiado tres enfoques principales respecto al tipo de política de ruteo que se efectúa [3]:
- A priori (política estática, offline).
- Dinámica (política de reoptimización, online).
- Mixta (política de descargue/abastecimiento preventivo).
En primer lugar se encuentra la política estática o a priori la cual se enmarca dentro de los procesos estocásticos de dos estados; en el primer estado se determina una secuencia de clientes (llamada ruta a priori) que deben ser visitados en ese orden por un vehículo, y en el segundo estado se ejecuta la ruta tal y como se definió. En caso que la ruta falle, se toma una acción recursiva. En la referencia [4] se propone una heurística cíclica obteniendo buenos resultados con base en la perspectiva del peor caso cuando la distribución de probabilidad de los clientes es idéntica. En la referencia [5] se propone una solución exacta del VRPSD utilizando el método entero L-Shaped; en la referencia [6] se utiliza un algoritmo evolutivo multiobjetivo y un método de simulación para el cálculo del costo de la ruta. En la referencia [7] se utiliza un método exacto para la solución del problema en donde la evaluación de la función objetivo se realiza mediante la simulación Monte Carlo. En las referencias [8] y [9] se implementa el método L-Shaped. En las referencias [10] y [11] se resuelve el VRPSD con múltiples con compartimentos utilizando algoritmos meméticos y evolutivos y heurísticas constructivas respectivamente.
En segundo lugar se encuentran las políticas dinámicas las cuales se formulan matemáticamente como un problema estocástico de múltiples estados. En la referencia [3] se utiliza la metodología de Programación Neuro-Dinámica. En la referencia [12] se resuelve el Problema de Ruteo de Vehículos con Capacidad y Demandas Estocásticas (CVRPSD) a través del método exacto branch and price. En la referencia [13] se utilizan heurísticas de reoptimización parcial. En las referencias [14] y [15] se desarrollan los algoritmos rollout para resolver el VRPSD con un solo vehículo bajo una aproximación dinámica. En la referencia [14] se utiliza un algoritmo rollout y simulación Monte Carlo para el cálculo de la función de costo. En la referencia [16] se presenta la estrategia paired-vehicle strategy para el VRPSD utilizando Búsqueda Tabú.
En tercer lugar se encuentra la política de descargue/abastecimiento preventivo. Esta política combina elementos de las políticas a priori y dinámica enmarcándose en un proceso estocástico de dos estados, en la cual el vehículo sigue una ruta a priori en el primer estado y a la vez está habilitado con reglas dependientes de estado que permiten reaprovisionamientos anticipados en el segundo estado. En la referencia [17] se resuelve el VRPSD con descargas preventivas para el caso de uno y múltiples vehículos, desarrollando las heurísticas route first-cluster next cluster first-route next. En la referencia [18] se prueba el impacto en el desarrollo de las metaheurísticas recocido simulado, búsqueda tabú, colonia de hormigas y algoritmos evolutivos, el uso de la distancia de la ruta a priori como una aproximación rápida de la función objetivo. En la referencia [19] se utiliza el híbrido Algoritmos Genéticos (GA) y búsqueda tabú para una aplicación real relacionada con la recolección de basuras en un área residencial de Malasia. En la referencia [20] se incorpora un elemento para el cálculo de la función objetivo basado en la técnica de optimización por simulación. En la referencia [21] se resuelve el VRPSD empleando las metaheurísticas PSO, GA y PSO con operadores genéticos.
El presente artículo está organizado de la siguiente manera. En la Sección 2 se define formalmente el VRPSD. En la Sección 3 se presenta el método de solución para el VRPSD. En la Sección 4 se presenta el banco de pruebas diseñado. En la Sección 5 se discuten los resultados computacionales obtenidos. Por último, en la Sección 6 se presentan las conclusiones de la investigación realizada.
2. DEFINICIÓN DEL PROBLEMA
En esta sección se define formalmente el VRPSD con descarga/abastecimiento preventivo.
Sea  un grafo completo, donde:
un grafo completo, donde:
 es el conjunto de nodos. El nodo
es el conjunto de nodos. El nodo  corresponde al depósito y los nodos
corresponde al depósito y los nodos  corresponden a los clientes.
corresponden a los clientes. , es el conjunto de arcos que conecta a los nodos.
, es el conjunto de arcos que conecta a los nodos. , denota la matriz de costo de viaje entre los nodos
, denota la matriz de costo de viaje entre los nodos  y
y  .
.
Se considera que la matriz 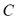 es simétrica y satisface la desigualdad triangular:
es simétrica y satisface la desigualdad triangular:  Además, todos los clientes tienen demandas estocásticas
Además, todos los clientes tienen demandas estocásticas  , con distribuciones de probabilidad conocidas. Se asume que el máximo valor de demanda del cliente
, con distribuciones de probabilidad conocidas. Se asume que el máximo valor de demanda del cliente  no excede la capacidad del vehículo
no excede la capacidad del vehículo 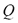 y tiene una distribución de probabilidad discreta
y tiene una distribución de probabilidad discreta  las variables aleatorias
las variables aleatorias  son independientes.
son independientes.
El objetivo del VRPSD considerando una política de descarga/abastecimiento preventivo consiste en encontrar una ruta a priori y una política de descargue/abastecimiento preventivo en cada nodo que minimice el costo total esperado. En este punto, es importante hacer una aclaración de los costos que se consideran para este problema:
- Costo de viajar desde un cliente hacia otro como se planeó.
- Costo de descargue: costo de regresar al depósito para realizar el descargue antes de visitar el siguiente cliente planeado.
- Costo de falla de la ruta: costo de regresar al depósito para realizar el descargue causado por la insuficiencia en la capacidad del vehículo para atender la demanda del cliente a visitar.
Una ruta a priori se denota como  para un vehículo en particular. Después de haber atendido al cliente
para un vehículo en particular. Después de haber atendido al cliente  , se asume que el vehículo tiene una carga residual
, se asume que el vehículo tiene una carga residual  y sea
y sea  el costo total esperado desde el nodo
el costo total esperado desde el nodo  hacia adelante. Si
hacia adelante. Si  representa el conjunto de todas las posibles cargas que un vehículo puede tener después de haber atendido al cliente
representa el conjunto de todas las posibles cargas que un vehículo puede tener después de haber atendido al cliente  , entonces
, entonces  para
para  satisface [2]:
satisface [2]:

En las ecuaciones (1)-(3),  representa el costo esperado de proceder directamente al siguiente nodo y
representa el costo esperado de proceder directamente al siguiente nodo y  representa el costo de la descarga/abastecimiento preventivo. Las anteriores ecuaciones se usan recursivamente con el propósito de determinar el valor de la función objetivo de la ruta planeada y la secuencia óptima de decisiones después de haber atendido a los clientes.
representa el costo de la descarga/abastecimiento preventivo. Las anteriores ecuaciones se usan recursivamente con el propósito de determinar el valor de la función objetivo de la ruta planeada y la secuencia óptima de decisiones después de haber atendido a los clientes.
La ecuación (4) representa la condición de frontera la cual quiere decir que el costo esperado después de haber visitado al último cliente de la ruta hacia adelante, independiente de la carga residual que tenga el vehículo en ese momento, es igual al costo fijo de ir del cliente  al depósito. En la literatura se presenta un enfoque tradicional para la evaluación del costo esperado de la función objetivo para el VRPSD con descarga preventiva basado en programación dinámica [17], las cuales arrojan buenas estimaciones del valor de la función objetivo, sin embargo, el costo computacional es elevado. Es por ello que el presente trabajo utiliza un enfoque basado en simulación Monte Carlo para evaluar la función objetivo.
al depósito. En la literatura se presenta un enfoque tradicional para la evaluación del costo esperado de la función objetivo para el VRPSD con descarga preventiva basado en programación dinámica [17], las cuales arrojan buenas estimaciones del valor de la función objetivo, sin embargo, el costo computacional es elevado. Es por ello que el presente trabajo utiliza un enfoque basado en simulación Monte Carlo para evaluar la función objetivo.
3. ENFOQUE DE OPTIMIZACIÓN POR SIMULACIÓN PARA EL VRPSD
El VRPSD es un problema de optimización combinatoria perteneciente a la clase NP-hard [7]. Encontrar soluciones óptimas a este problema implica contemplar, para cada una de las posibles permutaciones de clientes, todas las realizaciones de las demandas que éstos presenten. Es por ello que incluso para instancias pequeñas del VRPSD, la búsqueda de soluciones óptimas se convierte en una opción prácticamente inviable si ésta se realiza de manera exacta [18]. El presente trabajo utiliza el enfoque de Optimización por Simulación el cual busca determinar la mejor configuración de parámetros de entrada que alimenten al modelo de simulación produciendo resultados cercanos al óptimo [22] y [23].
En la literatura se destacan los trabajos de [7] y [20], los cuales utilizan Optimización por Simulación para el VRPSD con uno y múltiples vehículos. La Figura 2 presenta el framework SIM-EPSO propuesto en este trabajo para resolver el VRPSD, en el cual los módulos de optimización y simulación están dados por la metaheurística híbrida Optimización de Enjambre de Partículas Evolutivo (EPSO) y Simulación Monte Carlo, respectivamente. Cada una de las etapas correspondientes al módulo de optimización se discuten detalladamente en las siguientes secciones.
4. OPTIMIZACIÓN DE ENJAMBRE DE PARTÍCULAS EVOLUTIVO PARA EL VRPSD
El PSO es un método de optimización estocástico propuesto por [24] el cual se basa en imitar a nivel computacional el comportamiento social de individuos dentro de un grupo a partir de la interacción entre sus integrantes y de éstos con el entorno en el que se desenvuelven.
En el PSO cada partícula representa una solución potencial en el espacio de búsqueda, en donde cada una de ellas tiene asociado un valor fitness y una velocidad, que direccionan a las partículas hacia la solución. Un enjambre de partículas se representa de la siguiente manera:
Sea:

Durante el proceso iterativo las partículas actualizan sus posiciones y velocidades de la siguiente forma: Sea  la posición de la partícula
la posición de la partícula  -ésima en la dimensión
-ésima en la dimensión  -ésima en el momento
-ésima en el momento  . La posición de la partícula en el momento
. La posición de la partícula en el momento  se actualiza mediante la fórmula:
se actualiza mediante la fórmula:

donde,  es la velocidad de la partícula i -ésima en la dimensión
es la velocidad de la partícula i -ésima en la dimensión  -ésima en el momento
-ésima en el momento  . A su vez, la velocidad de cada partícula se actualiza mediante:
. A su vez, la velocidad de cada partícula se actualiza mediante:

aquí,  y
y  son los factores de aprendizaje cognitivo y social,
son los factores de aprendizaje cognitivo y social,  es un número aleatorio con distribución uniforme en el intervalo [0,1],
es un número aleatorio con distribución uniforme en el intervalo [0,1],  es el factor de inercia en el momento
es el factor de inercia en el momento  ,
, es la mejor posición personal de la partícula
es la mejor posición personal de la partícula  en el momento
en el momento  y finalmente,
y finalmente,  representa la mejor solución global del enjambre en el momento
representa la mejor solución global del enjambre en el momento  .
.
La velocidad de cada partícula a su vez conduce el proceso de optimización y tiene bajo consideración el conocimiento propio de ésta y el conocimiento social, resultado del intercambio de información de la vecindad de la partícula. El conocimiento propio de la partícula también es conocido como el componente cognitivo, el cual es proporcional a la distancia de la partícula desde su mejor posición encontrada, dado el primer movimiento realizado y se denota como  . El intercambio de información social se conoce como el componente social de la ecuación de velocidad, denotado como
. El intercambio de información social se conoce como el componente social de la ecuación de velocidad, denotado como  .
.
4.1. Representación de la Solución
El PSO fue concebido para resolver problemas de optimización con variables continuas y el VRPSD es un problema de optimización combinatoria; por lo tanto, es necesario explicar cómo se representa la solución en este caso y de qué manera se convierten las permutaciones de clientes en valores posición. Una solución del VRPSD  se convierte a valores posición usando la siguiente expresión propuesta por [25]:
se convierte a valores posición usando la siguiente expresión propuesta por [25]:

Donde:
 :
:  -ésima dimensión de la solución
-ésima dimensión de la solución  -ésima (cliente).
-ésima (cliente). :
:  -ésima dimensión de la partícula
-ésima dimensión de la partícula  -ésima en el espacio del enjambre (valor posición de cada cliente en la partícula).
-ésima en el espacio del enjambre (valor posición de cada cliente en la partícula).- rand(): número aleatorio generado mediante una distribución uniforme en [0,1].
 : número de clientes.
: número de clientes. : valor de frontera mínimo del valor posición de la partícula en el espacio del enjambre.
: valor de frontera mínimo del valor posición de la partícula en el espacio del enjambre. : valor de frontera máximo del valor posición de la partícula en el espacio del enjambre.
: valor de frontera máximo del valor posición de la partícula en el espacio del enjambre.
4.2. Decodificación de las soluciones del PSO
De igual forma se debe realizar el proceso inverso denominado decodificación de la solución PSO. La solución encontrada en el espacio solución PSO deberá decodificarse como una solución del problema original por medio de una permutación de clientes. Es por ello que los valores posición del vector  se convierten nuevamente a la solución codificada
se convierten nuevamente a la solución codificada  utilizando el Rank Order Value (ROV) [26]. El ROV es una técnica que convierte los valores continuos de las partículas en permutación de clientes. La conversión se realiza seleccionando el menor valor posición de la partícula y asignándole a éste el valor de 1. Luego, se selecciona el segundo menor valor posición y se le asigna el valor de 2 y así sucesivamente con los elementos restantes del vector posición. El vector resultante de este proceso, corresponde a la permutación de clientes proveniente del proceso iterativo del PSO.
utilizando el Rank Order Value (ROV) [26]. El ROV es una técnica que convierte los valores continuos de las partículas en permutación de clientes. La conversión se realiza seleccionando el menor valor posición de la partícula y asignándole a éste el valor de 1. Luego, se selecciona el segundo menor valor posición y se le asigna el valor de 2 y así sucesivamente con los elementos restantes del vector posición. El vector resultante de este proceso, corresponde a la permutación de clientes proveniente del proceso iterativo del PSO.
El Algoritmo 1 muestra los pasos para determinar la solución del VRPSD utilizando el PSO con operadores evolutivos (EPSO).
Algoritmo 1. EPSO aplicado al VRPSD
Algorithm 1. EPSO applied to the VRPSD
1: Inicializar las soluciones  usando la heurística del vecino más cercano
usando la heurística del vecino más cercano
2: Mientras el criterio de parada no se haya cumplido
3: Para 
4: Calcular el valor del fitness de 
5: Actualizar el  ,
, , si fitness de
, si fitness de  fitness de
fitness de 
6: Fin Para
7: Actualizar el  ,
, , si fitness de
, si fitness de  fitness de
fitness de 
8: Para 
9: Convertir la solución  en su valor posición usando la ecuación (7)
en su valor posición usando la ecuación (7)
10: Actualizar la posición  y la velocidad
y la velocidad  , de la partícula
, de la partícula  , usando las ecuaciones (5) y (6) respectivamente
, usando las ecuaciones (5) y (6) respectivamente
11: Convertir la partícula  en su permutación codificada usando ROV
en su permutación codificada usando ROV
12: Aplicar el operador de cruce usando el Algoritmo 2
13 Aplicar el operador de mutación usando el Algoritmo 3
14: Fin para
15: Fin Mientras
16: Establecer el  ,
, , como la mejor solución global
, como la mejor solución global
4.1. Operadores evolutivos
El PSO tiene varias limitaciones las cuales están asociadas principalmente a la configuración de los parámetros propios de la metaheurística [21]. Estos parámetros varían de un problema a otro, por lo que encontrar los valores óptimos no es una tarea sencilla.
Teniendo en cuenta lo anterior, en el presente trabajo se incorporan algoritmos evolutivos al PSO con el propósito de superar sus limitaciones. Mientras con el PSO se puede controlar en cierta medida la convergencia, los operadores evolutivos pueden garantizar una mayor diversidad de soluciones, lo cual hace que el enjambre se desplace hacia otra parte del espacio de búsqueda, evitando de esta manera una convergencia prematura. Para este trabajo se utilizó secuencialmente un operador de cruce simple el cual es aplicado a todo el enjambre con el  , seguido por un operador de mutación basado en el intercambio de genes. Los algoritmos 2 y 3 ilustran la implementación los operadores evolutivos de cruce y mutación respectivamente.
, seguido por un operador de mutación basado en el intercambio de genes. Los algoritmos 2 y 3 ilustran la implementación los operadores evolutivos de cruce y mutación respectivamente.
Algoritmo 2. Implementación del operador de cruce
Algorithm 2. Implementation of crossover operator
1: Para 
2: Seleccionar aleatoriamente un punto  entre 1 y
entre 1 y 
3: Intercambiar los valores de la solución codificada  con el
con el ,
, , i.e.
, i.e.  con
con 
4: Fin Para
Algoritmo 3. Implementación del operador de mutación
Algorithm 3. Implementation of mutation operator
1: Para 
2: Seleccionar aleatoriamente dos puntos  de la solución cruzada e intercambiarlos, i.e. intercambiar
de la solución cruzada e intercambiarlos, i.e. intercambiar  con
con 
3: Fin Para
5. BANCO DE PRUEBAS
En la literatura no es común realizar comparaciones con instancias benchmark para el VRPSD [18]. Por tal motivo, todas las instancias utilizadas en este trabajo fueron generadas de la siguiente manera: el depósito se encuentra ubicado en (0,0); para la generación de las demandas de los clientes, se consideraron 100 muestras, las demandas de los clientes siguen una distribución de probabilidad uniforme discreta. El banco de pruebas se construye teniendo en cuenta los factores que se definen en la Tabla 1.
En primer lugar se encuentra el número de clientes el cual toma el valor de 100 en el Nivel 1 y de 200 en el Nivel 2. Por otro lado, para el Nivel 1 la ubicación de los clientes está dada por una distribución uniforme en el intervalo [0,100], y para el Nivel 2 se asume que los clientes están ubicados aleatoriamente con distribución normal alrededor de dos centros (por lo que se tendrían dos clusters); la media y la desviación estándar para cada uno de los cluster se seleccionaron aleatoriamente mediante una distribución uniforme en el intervalo [0,100].
La distribución de las demandas de los clientes se genera teniendo en cuenta dos parámetros: la demanda promedio ( ) y la desviación estándar (
) y la desviación estándar ( ). Para los dos niveles, se asume que las demandas de los clientes siguen una distribución de probabilidad uniforme discreta en el intervalo
). Para los dos niveles, se asume que las demandas de los clientes siguen una distribución de probabilidad uniforme discreta en el intervalo  . La capacidad del vehículo se calcula teniendo en cuenta la formulación propuesta por [5] en el cual consideran que un factor que influye en la complejidad del problema es la cantidad de clientes atendidos por el vehículo en un solo recorrido, por lo que la capacidad está dada por la ecuación (8).
. La capacidad del vehículo se calcula teniendo en cuenta la formulación propuesta por [5] en el cual consideran que un factor que influye en la complejidad del problema es la cantidad de clientes atendidos por el vehículo en un solo recorrido, por lo que la capacidad está dada por la ecuación (8).

Donde  es el número promedio de clientes atendidos por el vehículo antes que éste realice la descarga preventiva. Para el Nivel 1 el valor de
es el número promedio de clientes atendidos por el vehículo antes que éste realice la descarga preventiva. Para el Nivel 1 el valor de  es igual a 4, y para el Nivel 2 de 8. El último factor definido es el umbral o política de descargue, el cual representa el nivel de carga residual que tiene el vehículo para realizar el descargue preventivo; en el Nivel 1 el umbral está dado por la media de la demanda del cliente
es igual a 4, y para el Nivel 2 de 8. El último factor definido es el umbral o política de descargue, el cual representa el nivel de carga residual que tiene el vehículo para realizar el descargue preventivo; en el Nivel 1 el umbral está dado por la media de la demanda del cliente  y en el Nivel 2 es igual al primer cuartil dentro de la distribución de demanda del cliente
y en el Nivel 2 es igual al primer cuartil dentro de la distribución de demanda del cliente  .
.
6. ANÁLISIS DE PARÁMETROS DEL EPSO
Con el propósito de determinar la configuración de parámetros del EPSO que condujera a mejores soluciones al VRPSD, se llevó a cabo un análisis de parámetros el cual se presenta en esta sección. Los parámetros asociados al EPSO son:

Para determinar la configuración de parámetros del EPSO que se utilizaron para correr los experimentos contenidos en el banco de pruebas, se realizaron simulaciones en las cuales, a través de variación de los valores de los parámetros, se obtenían los valores de la función objetivo. El criterio de selección de estos valores se basó en el menor valor de la función objetivo. La Tabla 2 presenta la configuración de parámetros establecida para este trabajo.
7. RESULTADOS COMPUTACIONALES
El algoritmo EPSO para resolver el VRPSD con descarga preventiva fue programado en Matlab 7.1 y ejecutado en un equipo con procesador Intel Core i3 y 4GB de RAM. En la Tabla 3 se encuentran los resultados del diseño experimental realizado. Cada experimento fue replicado cinco veces y las conclusiones se hacen con respecto al valor promedio de la función objetivo.
7.1 Análisis del diseño experimental
Para estudiar el efecto de los factores definidos en la sección 5 sobre el valor de la función objetivo, se propuso una serie de experimentos cuidadosamente diseñados para un banco de pruebas. Para ello, se llevó a cabo un diseño de Taguchi ortogonal 
que tiene ocho corridas experimentales, y con él se pueden estudiar desde dos hasta siete en dos niveles cada uno. En la Tabla 4 se muestran las estimaciones para cada uno de los efectos principales para el valor de la función objetivo.
Los efectos se muestran por orden de importancia para visualizar cuáles tienen un mayor impacto sobre el valor de la función objetivo. Aquí se observa que los factores  y
y  tienen un efecto positivo en la función objetivo; esto quiere decir que al pasar del nivel bajo (Nivel 1) al nivel alto (Nivel 2), el valor de la función objetivo aumenta. Por su parte, el efecto de los factores
tienen un efecto positivo en la función objetivo; esto quiere decir que al pasar del nivel bajo (Nivel 1) al nivel alto (Nivel 2), el valor de la función objetivo aumenta. Por su parte, el efecto de los factores  y
y  es negativo sobre la función objetivo al pasar del nivel bajo al nivel alto; lo anterior significa que cuando la capacidad del vehículo está en el nivel alto, la cobertura de clientes atendidos antes de la descarga preventiva aumenta, disminuyendo de esta manera el número de viajes al depósito por concepto de descargues preventivos o por fallas en la ruta. De igual forma, cuando los clientes están ubicados alrededor de dos centros, el valor de la función objetivo es menor con respecto a una ubicación de clientes con distribución uniforme en un área dada.
es negativo sobre la función objetivo al pasar del nivel bajo al nivel alto; lo anterior significa que cuando la capacidad del vehículo está en el nivel alto, la cobertura de clientes atendidos antes de la descarga preventiva aumenta, disminuyendo de esta manera el número de viajes al depósito por concepto de descargues preventivos o por fallas en la ruta. De igual forma, cuando los clientes están ubicados alrededor de dos centros, el valor de la función objetivo es menor con respecto a una ubicación de clientes con distribución uniforme en un área dada.
7.2. Comparación del rendimiento del algoritmo
En el presente trabajo se llevó a cabo un análisis adicional respecto a la calidad del algoritmo propuesto considerando dos criterios: valor esperado de la función objetivo y tiempo de ejecución. Estos valores fueron contrastados con la versión básica del PSO, como se observan en las tablas 5 y 6.
Como se observa, las soluciones obtenidas con el EPSO son superiores respecto al PSO para las ocho instancias comparadas, tanto en valor de función objetivo como en tiempo de ejecución. El éxito del EPSO sobre el PSO radica en la capacidad que tiene el primero en balancear tanto la explotación como la exploración en el espacio de búsqueda ya que hace que el enjambre evolucione a través de los operadores de cruce y mutación empleados, garantizando una mayor exploración en el espacio de búsqueda, aumentando de esta manera la posibilidad de encontrar mejores soluciones.
8. CONCLUSIONES
En el presente trabajo se propuso el framework SIM-EPSO con el propósito de dar solución al VRPSD con descarga preventiva, usando la metaheurística híbrida EPSO y simulación Monte Carlo. Debido a que en la literatura no existen instancias benchmark, se construyó un banco de pruebas utilizando un diseño experimental con un arreglo ortogonal  .
.
Además, se comparó el desempeño del EPSO con el PSO en donde se observó la superioridad del framework propuesto con respecto al segundo método de solución; revelando de esta manera, la capacidad que tiene el EPSO de realizar mejores exploraciones en la región factible y diversificaciones en las soluciones debido a los componentes de inteligencia de enjambre, propios del PSO y a los operadores evolutivos incorporados.
REFERENCIAS
[1] Arango, M. D., Adarme, W. and Zapata, J.A., Commodities distribution using alternative types of transport. A study in the Colombia bread SME's. DYNA, 163, pp. 222-233, 2010. [ Links ]
[2] Manfrin, M., Ant Colony Optimization for the Vehicle Routing Problem [Master thesis]. Université Libre de Bruxelles, 2004. [ Links ]
[3] Secomandi, N., Comparing neuro-dynamic programming algorithms for the vehicle routing problem with stochastic demands. Computers and Operations Research, 11-12, pp. 1201-1225, 2000. [ Links ]
[4] Bertsimas, D.J., A Vehicle Routing Problem with Stochastic Demand. Operations Research, 3, pp.574-585, 1992. [ Links ]
[5] Gendreau, M., Laporte, G. and Séguin, R., An Exact Algorithm for the Vehicle Routing Problem with Stochastic Demands and Customers. Transportation Science, 2, pp. 143-155, 1995. [ Links ]
[6] Tan, K., Cheong, C. and Goh, C., Solving multiobjective vehicle routing problem with stochastic demand via evolutionary computation. European Journal of Operational Research, 2, pp. 813-839, 2007. [ Links ]
[7] Rei, W., Gendreau, M. and Soriano, P. A, Hybrid Monte Carlo Local Branching Algorithm for the Single Vehicle Routing Problem with Stochastic Demands. Transportation Science, 1, pp. 136-146, 2010. [ Links ]
[8] Laporte, G., Louveaux, F. and Van Hamme, L., An integer L-Shaped algorithm for the capacitated vehicle routing problem with stochastic demands. Operations Research, 3, pp. 415-423, 2001. [ Links ]
[9] Hjorring, C. and Holt, J. New optimality cuts for a single-vehicle stochastic routing problem. Annals of Operations Research, 86, pp. 569-584, 1999. [ Links ]
[10] Mendoza, J.E., Castanier, B., Guéret, C., Medaglia, A.L. and Velasco., N. A memetic algorithm for the multi-compartment vehicle routing problem with stochastic demands. Computers & Operations Research, 11, pp.1886-1898, 2010. [ Links ]
[11] Mendoza, J.E., Castanier, B. and Guéret,C., Heuristics for the Multicompartment Vehicle Routing Problem with Stochastic Demands. Transportation Science, 3, 346-363, 2011. [ Links ]
[12] Christiansen, C. and Lysgaard, J. A branch-and-price algorithm for the capacitated vehicle routing problem with stochastic demands. Operations Research Letters, 6, 773-781, 2007. [ Links ]
[13] Secomandi, N., and Margot, F. Reoptimization Approaches for the Vehicle-Routing Problem with Stochastic Demands. Operations Research, 1, pp. 214-230, 2009. [ Links ]
[14] Novoa, C. and Storer, R. An approximate dynamic programming approach for the vehicle routing problem with stochastic demands. European Journal of Operational Research. 2, pp. 509-515, 2009. [ Links ]
[15] Secomandi, N., A rollout policy for the vehicle routing problem with stochastic demands. Operations Research, 5, pp.796-802, 2001. [ Links ]
[16] Ak, A., and Erera, L., A Paired-Vehicle Recourse Strategy for the Vehicle-Routing Problem with Stochastic Demands. Transportation Science, 2, pp. 222-237, 2007. [ Links ]
[17] Yang, W.H., Mathur, K. and Ballou, R., Stochastic Vehicle Routing Problem with Restocking. Transportation Science, 1, pp. 99-112, 2000. [ Links ]
[18] Bianchi, L., Birattari, M., Chiarandini, M., Manfrin, M., Mastrolilli, M., et al. Metaheuristics for the Vehicle Routing Problem with Stochastic Demands. Journal of Mathematical Modelling and Algorithms, 1, pp. 91-110, 2005. [ Links ]
[19] Ismail, Z., and Irhamah., Solving the Vehicle Routing Problem with Stochastic Demands via Hybrid Genetic Algorithm-Tabu Search. Journal of Mathematics and Statistics, 3, pp. 161-167, 2008. [ Links ]
[20] Tripathi, M., Kuriger, G. and Wan, H. An Ant Based Simulation Optimization for the Vehicle Routing Problem with Stochastic Demands. Proceedings of the 2009 Winter Simulation Conference, IEEE, 1969, pp. 2476-2487, 2009. [ Links ]
[21] Shanmugam, G., Ganesan, P. and Vanathi, P.T., Meta Heuristic Algorithms for Vehicle Routing Problem with Stochastic Demands. Journal of Computer Science, 4, pp. 533-542, 2011. [ Links ]
[22] Ólafsson, S. and Kim, J., Simulation Optimization. Proceedings of the 2002 Winter Simulation Conference. pp. 79-84, 2002. [ Links ]
[23] April, J., Glover, F., Kelly, J.P. and Laguna, M. Practical introduction to simulation optimization. Proceedings of the 2003 Winter Simulation Conference, 2003. [ Links ]
[24] Kennedy, J., and Eberhart, R., Particle Swarm Optimization. Natural Networks IEEE International Conference, pp. 1942-1948, 1995. [ Links ]
[25] Geetha, S., Ganesan, P., and Vanathi, P.T., A Hybrid Particle Swarm Optimization with Genetic Operators for Vehicle Routing Problem. Journal of Advances in Information Technology, 4, pp. 181-188, 2010. [ Links ]
[26] Liu, B., Wang, L. and Jin, Y., An effective hybrid PSO-based algorithm for flow shop scheduling with limited buffers. Computers & Operations Research, 35, pp. 2791-2806, 2008. [ Links ]




















