Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.80 no.180 Medellín July/Aug. 2013
THE PERFORMANCE OF SOME META-HEURISTICS IN CONTINUOUS PROBLEMS STUDIED ACCORDING TO THE LOCATION OF THE OPTIMA IN THE SEARCH SPACE
DESEMPEÑO DE ALGUNAS META-HEURÍSTICAS EN PROBLEMAS CONTINUOS ANALIZADOS SEGÚN LA POSICIÓN DEL ÓPTIMO EN EL ESPACIO DE BÚSQUEDA
RICARDO NAVARRO
M.Sc.; Department of Informatics, University of Holguín, Cuba, e-mail: rnavarro@facinf.uho.edu.cu
AMILKAR PURIS
Ph.D.; Department of Computer Science, University of Las Villas, Cuba, e-mail: ayudier@uclv.edu.cu
RAFAEL BELLO
Ph.D. Department of Computer Science, University of Las Villas, Cuba, e-mail: rbellop@uclv.edu.cu
Received for review January 29th, 2013, Accepted March 26th, 2013, final version June, 15th, 2013
ABSTRACT: Many hard optimization problems can only be effectively handled by meta-heuristic methods. Some continuous optimization problems have specific characteristics that demand a particular interest. These features include the location of the optima in a specific region of search space. Hence the main goal of this paper is assessing the performance of some outstanding population-based meta-heuristics on functions with optima on bounds and problems with optima off bounds. It is studied by taking a set of benchmark functions from the field of optimization as a point of departure.
KEYWORDS: continuous optimization, meta-heuristic, search space bounds
RESUMEN: Muchos problemas difíciles de optimización son abordables con eficiencia únicamente mediante técnicas meta-heurísticas. Algunos problemas continuos de optimización con características particulares requieren especial atención. Entre dichas características se encuentra la ubicación del óptimo en una región específica del espacio de búsqueda. De ahí que el propósito principal de este trabajo sea la evaluación del comportamiento de algunas meta-heurísticas poblacionales relevantes, tanto en funciones con óptimos en las fronteras del espacio de búsqueda como en problemas con óptimos fuera de las mismas. Ello es estudiado a partir de la aproximación de algunas funciones estándares de prueba.
PALABRAS CLAVE: optimización continua, meta-heurística, fronteras del espacio de búsqueda
1. INTRODUCTION
Optimization implies finding the best possible solution to certain problem. It can be regarded as a search for values of decision variables for which an objective function reaches its optimum value, either a minimum or maximum. Exact optimization methods are unfeasible on many large scale problems, even if they are P-class. Heuristic techniques are considered solutions to such limitations. Despite not guaranteeing the optimum solution, they easily guarantee a feasible one within a reasonable amount of time [12]; they are very useful in the case that the search space is too large and it is also for that reason that they are usually used in order to approximate NP-hard problems.
A meta-heuristic model is one that relies on some other heuristic ones to provide a solution to different sorts of problems. It is thus a multipurpose model intended to lead the heuristic ones towards promissory areas of the search space. Hence the application of the meta-heuristic approach to different optimization problems requiring just a few changes [1]. Among the most outstanding meta-heuristic models [12] there are some population-based methods such as Particle Swarm Optimization (PSO) and Genetic Algorithms (GA).
Optimization problems having particular features demand special attention. For instance, those in which the optima lies on search space bounds. Hence it is necessary to study the effectiveness of meta-heuristic methods upon such types of problems. It is also recommended to evaluate their performance on functions with optimum off bounds in order to determine the kind of problem they are more effective at solving, depending on the position of the optima.
2. TYPES OF PROBLEM ACCORDING TO THE LOCATION OF THE OPTIMA
A continuous optimization problem can be defined as a model P = (S, Ω, f ) where S represents a search space defined over a finite set of decision variables, Ω is the set of constraints between these variables and f : S →  is the objective function to optimize. The search space S consists of a set of continuous variables Xj ( j = 1,…, m) with real values vj in range [aj , bj]. Instantiation of a variable Xj is the assignment of a value vj to this variable and it is denoted by Xj ← vj.
is the objective function to optimize. The search space S consists of a set of continuous variables Xj ( j = 1,…, m) with real values vj in range [aj , bj]. Instantiation of a variable Xj is the assignment of a value vj to this variable and it is denoted by Xj ← vj.
A solution s ∈ S is then a complete assignment where the values of variables satisfy the constraints in Ω. A solution s* ∈ S is a global optimum if and only if • s ∈ S f (s*) ≤ f (s) (for the minimization case). Solving this sort of problem means finding at least one optima solution.
A specific type of continuous optimization problem is that where all vj for the optimal solution are at search space boundaries. Those bounds are determined by proximity to extreme values aj and bj for each variable, being such boundaries the ranges  and
and  , where ABj denotes its amplitude for variable Xj :
, where ABj denotes its amplitude for variable Xj :

As a complement for the type of problem described above, problems with optima out of bounds are defined as those where the optimum is located in the interior region of the search space. This region is represented by the range  , where oj is the value of the origin of the search space for the j-th dimension:
, where oj is the value of the origin of the search space for the j-th dimension:

and AIj denotes the amplitude of the interior region for variable Xj:

3. EXPERIMENTAL FRAMEWORK
This study's main purpose is to evaluate the effectiveness of some meta-heuristic methods both on problems with optima on search space bounds and on problems with optimum partly or fully out of bounds. Thus experiments were run on 28 benchmark functions, 10 of them with optima on bounds. Methods are mentioned next; problems are introduced as well, detailing most of those with optima on bounds.
The termination criterion for every method was the maximum number (M = D * 10000) of function evaluations, where D is the dimension of the problem (10, 30, 50) [10].
3.1. Meta-heuristic techniques
Because of their remarkable results, some population-based meta-heuristics from the state of art in continuous optimization were included in this study: the generic algorithm Cross generational elitist selection, Heterogeneous recombination and Cataclysmic mutation (CHC) [3], Steady-State Genetic Algorithm (SSGA) [11], Linearly Decreasing Inertia Weight in PSO (LDWPSO) [9] and Opposition-Based Differential Evolution (ODE) [8]. A recent but proficient method presented in [7] Variable Mesh Optimization (VMO) was also selected, as well as Covariance Matrix Adaptation Evolution Strategy with Increasing Population Size (G-CMA-ES) [2], which is a reference algorithm in this field as it was the best of all methods in 2005 CEC [4].
The parameters specified by the authors in all methods were used, except for VMO, which was mostly configured as detailed in [7] but its frontiers operator was redefined as a BLX-ab [5] based crossover, based on the results reported in [6].
3.2. Test functions
The applied test functions are minimization problems. Some of these (F1 - F7), all with optima on bounds, are described in Table 1.
The remaining problems (F5* - F25*) belong to the benchmark function set of the 2005 IEEE Congress on Evolutionary Computation (CEC). These problems are detailed in [10] as F5 - F25. Functions F5*, F8* and F20* have their respective optimum on bounds.
Most of the 28 selected benchmark problems are multimodal functions, only F1, F5 and F5* are unimodal ones.
3.3. Analysis of results
Next, results of statistical comparisons of the methods are discussed. The six meta-heuristics in study are repeatedly compared on sets of 10 functions with optima on bounds and of 18 problems with optima off bounds. Hence, the mean error of every method in the approximation of each function is measured. Thus, for both situations depending on the sort of problems, the groups (related to the methods) to be compared were built from data shown in Table A.I from Appendix A, corresponding to such measurements.
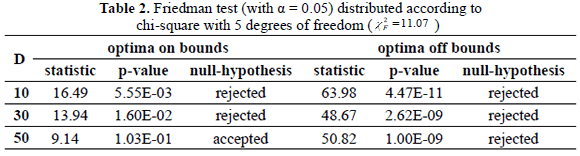
By using the Friedman test the performance of all methods is compared. If a significant difference among them is detected the Nemenyi test is applied post-hoc, to decide what methods are significantly different from each other. For all cases the null-hypothesis is that there is no significant difference among the behaviors of the algorithms in the comparison, i.e. they perform equally well. Results of the Friedman test are summarized in Table 2, while results of the Nemenyi test are represented in Figure 1. The null-hypothesis can be rejected by the Friedman test when its statistic is larger than the corresponding critical value ( in this study) or if its p-value is less than the significance level (a = 0.05). Besides, according to the Nemenyi test, two methods perform significantly differently if the corresponding average ranks differ by at least the critical difference (CD).
in this study) or if its p-value is less than the significance level (a = 0.05). Besides, according to the Nemenyi test, two methods perform significantly differently if the corresponding average ranks differ by at least the critical difference (CD).
On problems with optima on bounds the Friedman test detects significant differences among the methods for D = 10 and D = 30, but not for D = 50. It means that not all methods perform equally well for D = 10 and for D = 30, while according to such a test they do for D = 50. In every dimension ODE outperforms the remaining ones, but according to the Nemenyi test it is only significantly better than CHC for D = 10, and for LDWPSO in all cases, despite the result of the Friedman test for D = 50.
On problems with optima off bounds the Friedman test detects significant differences among them for all dimensions; at least two of the compared meta-heuristics perform significantly differently. As shown above, SSGA is the worst method in the study for this type of function; according to the Nemenyi test it is significantly outperformed by G-CMA-ES, VMO, ODE and CHC for both D = 10 and D = 30, as well as by G-CMA-ES, VMO and CHC for D = 50. On the other hand, LDWPSO is significantly outperformed by G-CMA-ES in all cases and also by VMO when D = 10. In addition, G-CMA-ES is significantly better than CHC for D = 10, while ODE is significantly outperformed by G-CMA-ES, VMO and CHC for D = 50.
4. CONCLUSIONS
Some research regarding performance of six outstanding population-based meta-heuristics is shown in this paper, taking into account their effectiveness on 10 benchmark problems with optima on bounds as well as on 18 benchmark functions with optima off bounds. The experiment was run for problems of 10, 30 and 50 dimensions. While it is not the main purpose of the current one, a scalability study should also include functions of larger dimensions. However, the functions studied can be useful to make an approximation of the scalability of these methods.
On problems with optima on bounds ODE is the method that performs best and which seems to be highly scalable. ODE did not perform well with optimum off bounds, in this case the best meta-heuristic is G-CMA-ES, appearing to be very scalable for this type of problem and also more effective and competitive. In addition, VMO proves to be more effective and scalable on problems with optima off bounds. On the other hand, LDWPSO, SSGA and CHC show the worst results. Both LDWPSO and CHC are as feasible for both types of problems, while SSGA proves better for problems with optima on bounds.
APPENDIX
Appendix A. Experimental results

REFERENCES
[1] Amaya, I., Cruz, J. and Correa, R. Real Roots of Nonlinear Systems of Equations through a Metaheuristic Algorithm, DYNA, 78(170), pp. 15-23, 2011. [ Links ]
[2] Auger, A. and Hansen, N. A Restart CMA Evolution Strategy with Increasing Population Size. Proceedings of the IEEE Congress on Evolutionary Computation, CEC 2005 Special Session on Real-Parameter Optimization. Edinburgh, UK, 1769-1776, September 2005. [ Links ]
[3] Eshelman, L. The CHC Adaptive Search Algorithm. How to have Safe Search when Engaging in Nontraditional Genetic Recombination, Foundations of Genetic Algorithms, 1, pp.256-283, 1991. [ Links ]
[4] Hansen, N. Compilation of Results on the 2005 CEC Benchmark Function Set. Institute of Computational Science ETH Zurich, Switzerland, May 2006. Available: http://www.ntu.edu.sg/home/EPNSugan [cited on June 10th, 2012] [ Links ]
[5] Herrera, F., Lozano, M. and Sánchez, A. A Taxonomy for the Crossover Operator for Real-Coded Genetic Algorithms: An Experimental Study, International Journal of Intelligent Systems, 18 (3), pp. 309-338, 2003. [ Links ]
[6] Navarro, R., Puris, A. and Bello, R. Optimización basada en Mallas Variables con cruce BLX-aß como Operador de Fronteras. Proceedings of the VI Conferencia Internacional de Matemática y Computación, COMPUMAT 2011. Santa Clara, Cuba, November 2011. [ Links ]
[7] Puris, A., Bello, R., Molina, D. and Herrera, F. Variable Mesh Optimization for Continuous Optimization Problems, Soft Computing, 16(3), pp. 511-525, 2011. [ Links ]
[8] Rahnamayan, S., Tizhoosh, H. and Salama, M. Solving Large Scale Optimization Problems by Opposition-Based Differential Evolution, IEEE Transactions on Computation, 7 (10), pp. 1792-1804, 2008. [ Links ]
[9] Shi, Y. and Eberhart, C. A Modified Particle Swarm Optimizer. Proceedings of the 1998 IEEE International Conference on Evolutionary Computation. Anchorage, Alaska, USA, pp. 69-73, May 1998. [ Links ]
[10] Suganthan, P.N., Hansen, N., Liang, J.J., Deb, K., Chen, Y.P., Auger, A. and Tiwari, S. Problem Definitions and Evaluation Criteria for the CEC 2005 Special Session on Real-Parameter Optimization. Technical report, Nanyang Technological University, Singapore, May 2005. Available: http://www.ntu.edu.sg/home/EPNSugan [cited on June 10th, 2012] [ Links ]
[11] Syswerda, G. Uniform Crossover in Genetic Algorithms. Proceedings of the Third International Conference on Genetic Algorithms. Fairfax, Virginia, USA, 2-9, June 1989. [ Links ]
[12] Talbi, E.G., Metaheuristics from Design to Implementation, John Wiley & Sons, New Jersey, 2009. [ Links ]