Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.183 Medellín Jan./Feb. 2014
https://doi.org/10.15446/dyna.v81n183.36171
http://dx.doi.org/10.15446/dyna.v81n183.36171
PATELLOFEMORAL MODEL OF THE KNEE JOINT UNDER NON-STANDARD SQUATTING
MODELO PATELOFEMORAL DE LA ARTICULACIÓN DE LA RODILLA BAJO SENTADILLA NO ESTÁNDAR
GUSZTÁV FEKETE
Ph.D., Laboratory Soete, Ghent University, Zwijnaarde, Belgium, Gusztav.Fekete@ugent.be
BÉLA MÁLNÁSI CSIZMADIA
C.Sc., Institute of Mechanics and Machinery, Szent István University, GödöllÅ, Hungary, Csizmadia.Bela@gek.szie.hu
MAGD ABDEL WAHAB
Ph.D., Laboratory Soete, Ghent University, Zwijnaarde, Belgium, Magd.AbdelWahab@ugent.be
PATRICK DE BAETS
Ph.D., Laboratory Soete, Ghent University, Zwijnaarde, Belgium, Patrick.DeBaets@ugent.be
LIBARDO V. VANEGAS-USECHE
Ph.D., Facultad de Ingeniería Mecánica, Universidad Tecnológica de Pereira, Pereira, Colombia, lvanegas@utp.edu.co
ISTVÁN BÍRÓ
Ph.D., Institute of Technology, Szeged University, Szeged, Hungary, biro-i@mk.u-szeged.hu
Received for review February 4th, 2013, accepted August 12th, 2013, final version September, 16th, 2013
ABSTRACT: The available analytical models for calculating knee patellofemoral forces are limited to the standard squat motion when the center of gravity is fixed horizontally. In this paper, an analytical model is presented to calculate accurately patellofemoral forces by taking into account the change in position of the trunk's center of gravity under deep squat (non-standard squatting). The accuracy of the derived model is validated through comparisons with results of the inverse dynamics technique.
Keywords: Patellofemoral forces, analytical model, modified squat, knee.
RESUMEN: Los modelos analíticos disponibles para calcular las fuerzas patelofemorales de la rodilla están limitados al movimiento estándar de cuclillas cuando el centro de gravedad es fijo horizontalmente. En este artículo se presenta un modelo para calcular con exactitud las fuerzas patelofemorales, teniendo en cuenta el cambio de posición del centro de gravedad del tronco durante una sentadilla profunda (posición de sentadilla modificada). Se valida la exactitud del modelo desarrollado mediante comparaciones con resultados de la técnica de dinámica inversa.
Palabras Clave: Fuerzas patelofemorales, modelo analítico, sentadilla modificada, rodilla.
1. INTRODUCTION
The widespread occurrence of various types of arthritis results in significant loss of manpower and immeasurable pain and suffering to many patients. Due to the limited understanding of the knee joint movement, clinicians have generally opted for a surgical solution that involves prosthetic replacement arthroplasty.
Analytical models related to the kinetics of the patellofemoral joint are still in short supply. Among the earliest models, Crowninshield et al. [1] and Andriacchi et al. [2] created quasi-static, analytical studies in order to determine the overall stiffness of the joint as a function of flexion angle. However, no investigation of the patellofemoral forces was actually carried out. The ratio between patellofemoral forces such as Fpf/Fq and Fpt/Fq (ratio of the patellofemoral compression force to quadriceps force and the patellar ligament force to quadriceps force, respectively) has been determined both by experimental methods [3] and with the help of various mathematical models [4, 5]. However, only the standard squat movement was investigated, where the forward movement of the trunk is not considered.
This work is part of a research that has been carried out at Szent István University and Ghent University, where analytical and experimental studies on the knee is being performed. It presents equations for the patellofemoral forces in the knee under non-standard squat, in which the centre of gravity moves both vertically and horizontally, thus the trunk movement during squatting is also considered.
2. EQUATIONS FOR PATELLOFEMORAL FORCES
The assumptions considered in deriving the equations of patellofemoral forces under standard squat are summarized as follows [6]: a) the model is quasi-static, b) it is two-dimensional, i.e., in the sagittal plane, c) contact forces are neglected, d) the femur and tibia are connected through a hinge with one degree of freedom, and e) the load is derived from the total weight of the person.
In this work, the movement of the trunk (i.e., the horizontal movement of the centre of gravity) is taken into account; therefore, the body weight vector (BW) can move vertically and horizontally. The movement of the centre of gravity is a known phenomenon; however, how much this movement alters the forces in the knee joint has not been investigated.
Furthermore, the movement of the femur and tibia are independent of each other (neither of them are fixed but can freely rotate during the squat). In this paper, the derived equations describe the forces connected to the femur, tibia, and patella under the non-standard squat as shown in Figure 1.
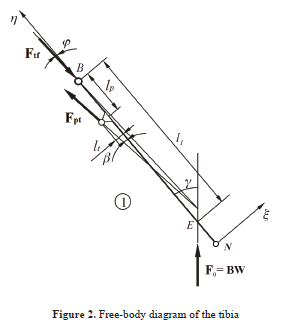
The arbitrary knee position, in Figure 1, is located at angle a. The BW force is derived from the body weight. The patella and the tibia are assumed to rotate about point B. The line of action BW intersects the theoretical line of the femur and tibia at points D and E. Rigid linkages represent the femur (3), the patella (2) and the tibia with foot (1).
The tibia is connected to the foot by a hinge of one degree of freedom (point N). The line of action of the centre of gravity intersects the femur at point D and the foot at point A. These points are not fixed, since the centre of gravity moves horizontally during a deep squat. At point D, a roller is assumed, which can move along the axis of the femur, while another roller is applied at point A, which can move along the axis of the foot. The rigid bodies are attached to each other by strings of negligible elastic elongation. The free-body diagrams of the three elements are shown in Figures 2, 3 and 4.
The model includes several constants and variables: the notations of the geometric lengths are listed in Table 1.
The moment equation applied about the z-axis through point B on the tibia (Figure 2) is:

From Eq. (1), the patellar tendon force (Fpt) can be derived as:

In order to simplify the results, dimensionless parameters are introduced (Table 2).
By the introduction of these quantities, the normalized force in the patellar tendon is:
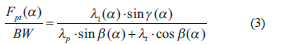
The scalar equilibrium equations related to the
x - h coordinate system (fixed to the tibia) are in the following form (Figure 2):

Where Ftf is the tibiofemoral compression force and j (a) is the angle between the axis of the tibia and the tibiofemoral force vector. By substituting Eq. (3) into Eqs. (4) and (5), Fpt is eliminated. After this, Eq. (4) is set to Ftf, and then it is substituted into Eq. (5). The substitution is followed by some additional simplifications, and finally the angle j (a) can be derived as:

By the use of j (a), the tibiofemoral force can be derived from Eq. (4) or Eq. (5) as:

After deriving the Fpt and Ftf forces, Figure 3 is considered.
Applying the moment equilibrium equation about the z axis through point B on the femur (Figure 3) gives:

Taking into account that d = a - g, and assuming y » 0, from Eq. (8), the quadriceps force in the tendon becomes:
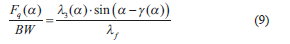
The scalar equilibrium equations related to the patella in the x - y coordinate system (Figure 4) are:
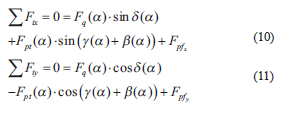
Where Fpfx and Fpfy are the components of the patellofemoral compression force in the x and y directions, respectively.
From Eq. (9) and Eq. (10), the magnitude of the patellofemoral compression force is:

For a given BW force and angle a, Eqs. (3), (7), (9), and (12) can be used to determine Fpt (a),
Ftf (a), Fq (a), and Fpf (a), respectively.
The parameters appearing in the above mentioned equations have been experimentally determined [7, 8] and summarized in Table 3.
3. RESULTS AND DISCUSSION
As it has been proven by other authors [5, 6], the patellofemoral forces directly depend on the net knee moment; this is a moment about the instantaneous centre of rotation of the knee joint generated by the body weight, in the case of the standard (or non-standard) squat.
Therefore, it is interesting to see how this moment depends on the position of the centre of gravity. By the use of inverse dynamics approach [9, 11, 14] all the movements of the human body can be taken into consideration, thus the effect of the centre of gravity may also be considered. By knowing (measuring) the kinematics of a person during non-standard squat, the measured forces will involve the effect of the moving centre of gravity as well. For this reason, the results are best compared to the results of inverse dynamics method.
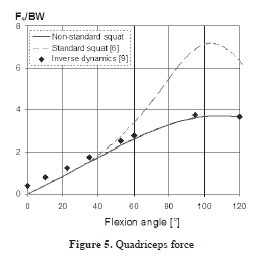
In Figure 5, the quadriceps tendon force of the non-standard squat model corresponds well with the inverse dynamics result of Sharma et al. [9] found in the literature.
The peak force of the non-standard squat model is estimated to be 3.63 BW at 120°°, while the standard squat model predicts a peak magnitude of 7.2 BW and peak location between 90° and 100° of flexion angle.
In practice, human subjects lean forward during squatting, which, apart from helping them to keep their balance, also reduces the patellofemoral forces. This is the reason why every experimental, analytical, or numerical model, which does not incorporate the moving of the centre of gravity tends to overestimate the net knee moment, and results in higher forces in the quadriceps (and in the other muscles or tendons).
All the same, this parameter has only been investigated by Kulas et al. [10], therefore, up to now there has been a very limited amount of information about how the horizontal movement of the centre of gravity influences the patellofemoral forces.
In Figure 6, the patellar tendon force is plotted. The correlation between the standard [6] and non-standard models regarding this force is strong. Their characteristics, magnitudes, and peak locations are in good agreement with each other. According to these corresponding results, the estimated peak force is 6.8 BW and the peak location is at 120° of flexion angle. It has to be mentioned that this is the only force whereupon the movement of the centre of gravity had a relatively small effect.
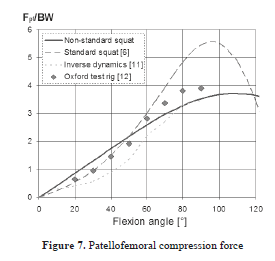
In Figure 7, the patellofemoral compression force is plotted. By considering the plotted results, the non-standard squat model correlates with the results of Escamilla et al. [11] and Churchill et al. [12]. The estimated peak angle of the non-standard squat model, in this case, is located around 110° of flexion angle and the peak force is approximately 3.6 BW. However, it should be noted that the result of Escamilla et al. [11] was carried out only up to a 90° flexion angle. If we compare the standard squat results with the results provided by the inverse dynamics method and the non-standard squat model, the significant difference related to this force becomes quite apparent.
The standard squat model is created with similar boundary conditions as an Oxford-type test rig [6], therefore, the apparent difference between the standard and non-standard squat is likely due to this type of modelling technique: according to this method the quadriceps muscles are detached from the femur, and the knee capsule is removed, thus the entire BW is applied solely through the quadriceps tendon and patellar tendon. Therefore the entire knee moment, due to the BW is supported by the patella, and the resulting loads may be higher than physiological loads [6]. Further, during a squat motion, the human subject can lean forward to move the centre of mass forward and tilt the hip reducing the joint moment and can therefore lower the patellofemoral force significantly. The standard squat approach assumes that the subject stays perfectly vertical maximizing the knee moment and maximizing the quadriceps force. Finally, the knee moments in Oxford rig studies are often lower than physiological knee moments. The values reported using inverse dynamics method do not suffer from these factors.
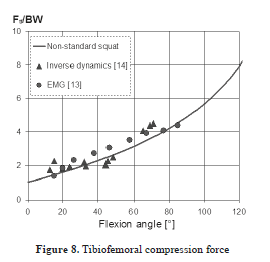
In Figure 8, the tibiofemoral force is presented. The standard squat model [6] is not able to predict this force, thus no comparison could be carried out between the two analytical models.
The new non-standard squat model was compared to the results of Zheng et al. [13] and Steele et al. [14]. As it may be observed, the three results are in agreement, although the experimental result of Zheng et al. [13] and Steele et al. [14] provide predictions only until 90° and 70° of flexion angle. Here, the peak force is estimated as 7.8 BW.
In order to determine the influence of moving the centre of gravity in numbers, the patellofemoral forces have been calculated and compared as a percentage difference between the standard and non-standard squat:

Where, K can be any quantity (force, moment or displacement). DK can provide a percentage difference of a standard quantity compared to a non-standard quantity (here standard and non-standard relates to the squat motion). The obtained results were summarized in Table 4.
The incorporation of the trunk movement significantly lowers the patellofemoral forces (up to 46%) along the calculated domain. This lowering effect on the patellofemoral forces (average 20%) corresponds very well with the result of Kulas et al. [10] who also investigated the effect of moderate forward trunk lean condition and observed 24% lower peak forces in the anterior cruciate ligaments (ACL).
Although, no direct measurement was performed to validate the obtained results, the comparison between the current predictions and the inverse dynamics data found in the literature show appropriate agreement.
The most important feature, which has to be underlined, is the possibility to include the movement of the trunk into the model.
4. CONCLUSIONS
In summary, a new analytical model is presented, which draws the attention to the effect of the movement of the centre of gravity on the knee joint kinetics. This model is capable of accurately predicting the patellofemoral, tibiofemoral, patellar ligament, and quadriceps forces in the knee during standard or non-standard squatting motion.
The new analytical model is derived from theoretical assumptions and experimentally determined parameters based on multiple human participants. The results of the analytical model correlated well with inverse dynamic results taken from the literature.
This new model is limited to the description of the kinetics of squatting motion. More specifically, the model shows how the horizontal movement of the centre of gravity influences the patellofemoral forces, since this phenomenon has not yet been investigated thoroughly by any other author. In addition, the model may be used to easily investigate other types of squat (depending on the l functions), while the inverse dynamics method requires a measuring system and programs to determine the forces.
Through the modelling approach, together with the creation of the necessary equations, similar modelling issues become more understandable and solvable.
Among the patello- and tibiofemoral forces, the obtained Fq(a) force function can be extended for further use as an input function for isometric motion, since most descriptive relationships
[3, 4] found in the literature provide only the ratio of the patellofemoral forces divided by the quadriceps force.
As a further step, a numerical model will be built in MSC.ADAMS using a moving centre of gravity, since the necessity of this parameter is proven by this analytical model. In addition to this feature, the MSC.ADAMS model will be used to investigate the contact forces (friction and normal) between the connecting surfaces and the sliding-roll ratio. These quantities will be given as a function of flexion angle.
ACKNOWLEDGEMENTS
The study was supported by the FWO (project number: G022506), the Universiteit Gent - Labo Soete, and the Szent István University - Faculty of Mechanical Engineering and Mechanical Engineering Ph.D. School.
REFERENCES
[1] Crowninshield, R., Pope, M.H. and Johnson, R.J., An analytical model of the knee. Journal of Biomechanics, 9 (6), pp. 397-405, 1976. [ Links ] [2] Andriacchi, T.P., Mikosz, R.P., Hampton, S.J. and Galante, J.O., Model studies of the stiffness characteristics of the human knee joint. Journal of Biomechanics, 16 (1), pp. 23-29, 1983. [ Links ] [3] Miller, R.K., Murray, D.W., Gill, H.S., O'Connor, J.J. and Goodfellow, J.W., In vitro patellofemoral joint force determined by a non-invasive technique. Clinical Biomechanics, 12 (1), pp. 1-7, 1997. [ Links ] [4] Van Eijden, T.M.G.J., Kouwenhoven, E., Verburg, J. and Weijs, W.A., A mathematical model of the patellofemoral joint. Journal of Biomechanics, 19 (3), pp. 219-229, 1986. [ Links ] [5] Cohen, Z.A., Roglic, H., Grelsamer, R.P., Henry, J.H., Levine, W.N., Mow, V.C. and Ateshian, G.A., Patellofemoral stresses during open and closed kinetic chain exercises - An analysis using computer simulation, The American Journal of Sports Medicine, 29 (4), pp. 480-487, 2001. [ Links ] [6] Mason, J.J., Leszko, F., Johnson, T. and Komistek, R.D., Patellofemoral joint forces. Journal of Biomechanics, 41 (11), pp. 2337-2348, 2008. [ Links ] [7] Fekete, G., Csizmadia, B.M., Wahab, M.A. and De Baets, P., Experimental determination of horizontal motion of human center of gravity during squatting, Experimental Techniques, doi:10.1111/ j.1747-1567.2011.00768.x. [ Links ] [8] Fekete, G., Kinetics and kinematics of the human knee joint under standard and non-standard squat movement. PhD Thesis, Ghent University, pp. 101-133, 2013. [ Links ] [9] Sharma, A., Leszko, F., Komistek, R.D., Scuderi, G.R., Cates, H.E. and Liu, F., In vivo patellofemoral forces in high flexion total knee arthroplasty. Journal of Biomechanics, 41 (3), pp. 642-648, 2008. [ Links ] [10] Kulas, A.S., Hortobágyi, T. and DeVita, P., Trunk position modulates anterior cruciate ligament forces and strains during a single-leg squat. Clinical Biomechanics, 27 (1), pp. 16-21, 2012. [ Links ] [11] Escamilla, R.F., Zheng, N., MacLeod, T.D., Edwards, W.B., Hreljak, A., Fleisig, G.S., Wilk, K.E., Moorman III, C.T. and Imamura, R., Patellofemoral compressive force and stress during the forward and side lunges with and without stride. Clinical Biomechanics, 23 (8), pp. 1026-1037, 2008. [ Links ] [12] Churchill, D.L., Incavo, S.J., Johnson, C.C. and Beynnon, B.D., The influence of femoral rollback on patellofemoral contact loads in total knee arthroplasty. Journal of Arthroplasty, 16 (7), pp. 909-918, 2001. [ Links ] [13] Zheng, N., Fleisig, G.S., Escamilla, R.F. and Barrentine, S.W., An analytical model of the knee for estimation of internal forces during exercise. Journal of Biomechanics, 31 (10), pp. 963-967, 1998. [ Links ] [14] Steele, K.M., DeMers, M.S., Schwartz, M.H. and Delp, S.L. Compressive tibiofemoral force during crouch gait. Gait & Posture, 35 (4), pp. 556-560, 2012. [ Links ]