Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.81 no.187 Medellín Sept./Oct. 2014
https://doi.org/10.15446/dyna.v81n186.46105
http://dx.doi.org/10.15446/dyna.v81n187.46105
Reliability in urban freight distribution: A Markovian approach
Confiabilidad en distribución urbana de mercancías: Un enfoque Markoviano
Miguel Gastón Cedillo-Campos a, José Luis de la Riva-Canizales b, Alfredo Bueno-Solano c, Jesús Gonzalez-Feliu d & Jorge Luis García-Alcaraz e
a, c Mexican Institute of Transportation, Querétaro, México. gaston.cedillo@mexico-logistico.org, abueno@imt.mx
b COMIMSA - CONACYT (National Council of Science and Technology), Saltillo, Coahuila, México.
d Centre National de la Recherche Scientifique, Lyon, France. jesus.gonzalez-feliu@cnrs.fr
e Institute of Engineering and Technology - Autonomous University of Ciudad Juarez, Ciudad Juarez, México. jorge.garcia@4uacj.mx
Received: May 28th, 2014.Received in revised form: August 25th, 2014.Accepted: September 10th, 2014
Abstract
A key element in assessing reliability in urban freight distribution (UFD) is the probability density function (PDF) of the variables that characterize the performance of the distribution routes. This article presents a method for modeling the PDF with an approach based on the Markov models, under the assumption that the present status of reliability of a route depends only on its immediate previous state. Currently, the PDF is obtained directly from the field, therefore an analytical model that provides certainty to the analysis is essential. The results are applicable both to the design of routes and operation of the same process. The originality of this work is based on the development of a methodological procedure to assess the reliability of the components of a path, complementary to current methodologies to calculate network reliability.
Keywords: Reliability; Markov models; urban freight distribution; logistics; supply chain.
Resumen
Un elemento importante en la evaluación de la confiabilidad de la distribución urbana de mercancías (DUM) es la función de densidad de probabilidad (FDP) de las variables que caracterizan el desempeño de las rutas de distribución. En este artículo se presenta un método para modelar la FDP con un enfoque basado en los modelos de Markov, bajo el supuesto de que la situación actual de la confiabilidad de una ruta sólo depende de su estado inmediato anterior. Actualmente, la FDP se obtiene de forma empírica, por lo tanto, un modelo analítico que proporcione seguridad en el análisis es esencial. Los resultados son aplicables en el diseño de rutas y el funcionamiento del mismo proceso. La originalidad de este trabajo se basa en el desarrollo de un procedimiento metodológico para evaluar la confiabilidad de los componentes de una ruta, la cual es complementaria a las metodologías actuales para calcular confiabilidad en redes.
Palabras clave: Confiabilidad; modelo de Markov; distribución urbana de mercancías; logística; cadena de suministro.
1. Introduction
An urban freight distribution system with an incorrect design can sometimes cause an increase of up to 5% on the invoiced value of the goods, and also degrades the quality of service expected by the client [1,2]. Companies benefit from the important advantages of high agglomeration of production and consumption activities located within cities, (considered as entities with a greater influence in the dynamism of transport and its development). But at the same time, this means important challenges imposed by extern factors such as congestion of traffic and other barriers for the effective distribution of its products [3-6]. In this sense, the urban freight distribution (UFD) must at the same time adapt to new forms of consumption, and also adjust to the urban territory's transformations that put new barriers to logistics operations [7-9].
Requirements of an agile coordination of human, material and financial resources at the UFD require establishing a well-structured plan of logistics operations. Otherwise, there is a risk of unexpected costs that would not only be reflected in the final price of a product, but also in a poor exposure and lost sales. Wishing to guarantee an effective logistics performance, a key factor is to know the level of operation of the system both in stable and uncertain states [10]. In fact, according to [11]: "in addition to factors such as time and cost, logistics performance increasingly depends on the reliability and predictability of the supply chain." So "the reliability of the supply chain is one of the most important aspects in logistics performance".
Reliability in UFD is considered as: "the level of stability in the quality of the service offered by a system of routes" [12]. It is also known as distribution system robustness [13]. In this regard, a key element in assessing network reliability is the probability density function (PDF) of the variables that characterize the performance of the distribution routes, which is currently calculated empirically. This is why an analytical model is necessary.
This research contributes to the body of knowledge in the area, by offering a methodology for evaluating the reliability of the components of a distribution route, modeling the PDF on the basis of the Markov models. Accordingly, this contribution assumes that the current state of reliability of a route depends only on its immediate previous state. In this context, two main problems were identified to be solved for the analysis of reliability of a UFD network: 1) to determine its reliability and vulnerability to ensure an operational level of service; and 2) dynamically re-design the system of distribution routes considering predetermined restrictions regarding its set of nodes and edges. Given the scope of the topic, this article focuses on the resolution of the first issue. That is, with the objective of evaluating the reliability of the components of a UFD route, a modeling method of the PDF based on the theory of Markov models is exposed.
This document is structured as follows. In the following section 2, a critical analysis of previous approaches, and evaluation techniques reported in the literature is presented. Section 3 outlines the methodology used, emphasizing the phase of application of the Markov models. Section 4 presents the application of this methodology to a case study. Finally, section 5 presents relevant conclusions, as well as future research work.
2. Background
In the context of commercial distribution, the UFD activity is considered as the set of processes performed through the distribution chain, from the origin until the reception by the customer within an urban area [14]. In this sense, looking for improved distribution systems, decision makers are not only facing the definition of the location of warehouses and sale points, transportation, inventory level, but also the selection of distribution routes, all under a set of given restrictions [7].
In this regard, different strategies to improve the urban freight distribution have been implemented in recent years, among them: i) improvements in the processing of orders and customer service; ii) processes and operations of reverse logistics; iii) implementation of logistics operators with dedicated fleets; iv) location of logistics support in logistics centers, many-to-many delivery, multiple shipments, among others [11,15]. All these have been originated and modified routing design methods. The literature reports three classes of methods: 1) exact; 2) heuristics; and; 3) meta-heuristics methods [16].
2.1. Networks reliability
The analysis of network reliability has commonly focused on different aspects of the distribution and transport, such as: i) the reliability of connectivity (or terminal reliability, which means that distribution can be successfully completed between each pair of nodes); ii) reliability of the travel time (including the transportation of goods with success at a given time); and iii) the reliability of capacity (which considers the distribution adapted to a demand of traffic or load). All of them are associated with probabilities of occurrence of each event [17-18].
Another important aspect is also the vulnerability of networks. This latest is related to observable consequences in the distribution due to any failure or disruption on routes regardless of its probability of occurrence. These two concepts (reliability and vulnerability) are differentiated when considering the reliability as the operability level of the system, and vulnerability as the consequences of the non-operability [19].
Among the consequences of a distribution system with a low reliability, it is possible to observe: i) increase in the transit time of the goods; ii) loss of opportunity value; iii) total or partial default order; and iv) need to implement crisis plans. All these generate socioeconomic costs that were not previously considered.
2.2. Reliability evaluation methods
This paper defines a measure of reliability of a distribution system based on its topology and on the reliability of its components. One of the important elements to assess network reliability is the stage of defining the parameters or reliability indicators. The main common indicators are: 1) frequency of interruption, which indicates how many times a route has been disrupted over a period of time; 2) unavailability of the network, which measures the total time of disruption for a route over a period of time; 3) duration of disruption; [20].
However, another important indicator is the probability of failure, for which there are analytical methodologies and simulations. Among those with a focus on simulation, Monte Carlo technique is used. It should be noted that, meta-heuristics and genetic algorithms techniques are also used. On the other hand, the focus of analytical methods, include: i) techniques of frequency and duration; ii) minimum-cut method; iii) fault tree analysis; iv) Markov models; v) Boolean models; vi) the generating function [21].
However, these methodologies require the reliability value of each component of the route to determine the reliability of the whole route. All of them lack a procedure for evaluation; however, the Markov models were identified as an important base to measure the reliability of the every component through its PDF. Markov models are characterized by a logical approach to model complex systems and sequential events [22].
Since our research assumed that the current state of reliability of a route only depends on its immediate previous state, an approach based on the Markov models was appropriate. At the same time, we considered that taking samples of the reliability state of a route, at different moments, and if these samples are related to some indicators, it is then possible to make a dynamic analysis (feature which is lacking in other methods). A Markov model applied to the subject of distribution is defined as a stochastic model of evaluation of reliability, associated with one of the default states of operation or not [22,23]. However, it is important to note that Markov models allow obtaining the probability that the route resides in any of its possible states, but not the probability of failure or disruption at some certain time of operation.
3. Methodology
The methodology oriented to reliability assessment here exposed is composed by 3 stages: i) Evaluation of reliability factors; ii) Markov models; and iii) Evaluation of the path reliability.
3.1. Evaluation of reliability factors
The first phase determines the variables to consider as factors of reliability of a route. Based on the approach of reliability analysis (connectivity, travel time or capacity), these factors are specified by considering as route failure any incident or disruption that affects the optimal or expected operation of the route. Among some of the variables observed are: i) time; ii) reaction capacity; iii) cost of operation by unit transported; iv) effective deliveries; v) load capacity, etc.
For each unit of time during which the measurements of the reliability factors are carried out, an indicator, called reliability indicator, must represent them. To integrate this indicator, we must linearly combine all the study factors that consider as coefficients the importance weightings of each variable. Furthermore, to determine the reliability of the elements or nodes that make up the distribution route, it was due to obtain an indicator of reliability for each of them.
3.2. Markov models
In a second phase, Markov models were applied to estimate the reliability of each item (node) of the route. This was based on the measurements of the reliability factors, as well as on the reliability indicator [24]. This approach was organized around four parts:
a) Definition of the states of the process and mechanisms of transition between them
The performance states of the route can be defined a priori or a posteriori of the measurements of the reliability indicator. Consequently, based on [23,25] the characteristics of the process were identified to define the mechanisms of transition between states. Therefore, if the probability that the process currently in a certain state changes to another state, we then say that the process is:
- Recurrent: If the probability is the same for two or more units of time;
- Transitional: If the probability is different for any two units of time;
- Periodical: If the probability is the same for any period of unit of time;
- Absorbent: If the probability is zero in any unit of time;
- Complex: If the probability is different to zero in any unit of time.
b) Selecting the Markov model
There are other attributes of the process to determine the type of model to be used when modelling a phenomenon.
First, it is important to confirm that the phenomenon is consistent with a behavior of Markov chains. This way, based on the frequency of measurements of the variables of the process and the classification of the possible states of the process, the type of Markov model is stated [20,22].
Another important feature of the model is its homogeneity, i.e., the probability that the process currently in one of the states changes to another particular state is the same, regardless of the time in which the variables of the phenomenon are evaluated [19,22].
c) Determining the probabilities of transition
The probabilities of transition between states indicate the probability of the process X to go from a state i to state j for each unit of time n [23], which are expressed as follows:

Then, for the case in which the probability of the process of going from state i to state j for k units of time is needed, the expression to compute it is [24]:

Based on the characteristics and type of Markov model, as well as on the reliability of the process indicator measurements, transition probabilities were obtained [20], which in turn formed the transition matrix:

d) Analysis of the temporal evolution of the phenomenon
This process is understood as predicting the state of a process at a certain time through transition matrices [22]. However, the analysis depends on the type of model:
- In the case of a discrete Markov chain, the transition matrix of k units of time is as follows:
Where each component of the matrix is the probability of transition from one state to another in k units of time. If the discrete Markov chain is homogeneous, it is because:
- In the case of a continuous Markov chain, one of the techniques to analyze this type of stochastic processes is to solve differential equations [24,25]. Since the process is represented by a succession of values X (t) representing the value of the process X at any moment of time t, then the probability of transition from one state i to state j, was defined as:

Where, the matrix of transition was established as:

Therefore, considering a homogeneous Markov chain, we obtained that the probability of each state at time t + h was the linear combination of the probabilities of all states at time t and the transition probabilities in infinitesimal time interval (Dt) defined as lijDt:

Based on the property that the sum of the probabilities of transition from one state to the other, the process is:

The result was that by replacing (7) in each equation (8) for each state, the equations system is:

From which, applying algebra we obtained the following matrix system:

By solving this differential equations system, and considering the initial conditions of the process, the result is a system solution vector in which its components are the PDF of reliability states.

3.3. Evaluation of the path reliability
In a third phase, once obtained the calculation of reliability of each node that is part of the distribution path, the reliability of the distribution network is computed. To do so, algorithms to assess the network reliability were used. An option was implementing the hybrid algorithm proposed by Jane Chin-Chia [26]. It not only calculates the reliability of a route, but also of all feasible routes based on nodes, edges, demand and distribution costs. It also displays a direct and practical reliability assessment.
The purpose of this algorithm is to compute the reliability of the route by organizing its components as reliable, not reliable, or stochastic, through the analysis of the characteristics of the route, stored in a S-item. The algorithm starts by considering as stochastic all possible routes formed by feasible nodes and edges for the distribution. Through iteration the classification of each route is determined. Finally, the algorithm ends when the S-item is absent from any stochastic route.
In the process of determining if a route is reliable or not, the reliability portion issued by this route is added to the network reliability on the previous iteration. If it is considered as stochastic, then each component of this route is analyzed to determine what parts are reliable or not, ending with the calculation of reliability of the route.
4. Application and analysis
To show the importance of the exposed work, a case study was used. The ABC Company is dedicated to the delivery and collection of mail and parcel service. It wishes to fulfill in time and form the service expectations offered to the customer. The approach used was mainly based on the assessment of reliability in the sense of connectivity and delivery time. Due to the variability of the demand, the company required assessing the reliability for each day in order to design an optimal route. Accordingly, the company looked for designing a route from s to t (see Fig. 1).
After a sampling of failures at each node in the route during 12 days (two weeks of six working days each), with ten delivery vehicles, the following items were observed: i) average failure time; ii) deliveries affected by failures; and iii) availability of the route due to failure (see Table 2).
Although the type of failure or disruption was considered independent in this analysis of reliability, it is relevant to mention what events were counted as failures: i) mechanical failures; ii) traffic congestion; iii) road accidents; iv) loss of time due to ignorance of the route.
From the information collected, there were reliability indicators for each time period and each day. This information is presented in Table 3, by means of the following equation (based on the classification of States):

Where VC (X) is the critical value of the variable X, which indicates the tolerance limit of X because of shortcomings in each period of time. For the case study, these are:
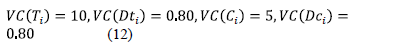
Once evaluated the reliability indicators, the PDF were determine for each state of the process; that is to say initiating the phase of Markov models to define the states of reliability (see Table 4).
The characteristics of the phenomenon related to the properties of Markov models were also took into account. Considering that the process is transitory, absorbed in state E and reducible due to state E, Table 5 is obtained, showing the encoding of the I(t).
Since the experiment was conducted during continued business days with consecutive units of time (with a discrete classification of states; and in compliance with the property of Markov, where the current state of the process depends only on the state during the previous time unit), to work with a continuous Markov chain was chosen.
Taken into account the ratios of change from one state to another, the transition matrix A was defined based on the coding of Table 4, which is represented as:

For example, the process appears 33 times in state A (excluding states from final time t16), but once in it, the process only remains in state A 13 times. So the transition probability is 0.393.
For the last part of the Markov modeling, the differential equation system was solved (DES). This system is representative of the reliability behavior of node 1. So the DES is represented as:

Since the DES is linear and homogeneous with constant coefficients, to solve the eigenvalues and eigenvectors of the matrix associated with the DES, the eigenvalues were obtained by using the MATLAB® language:

While the eigenvectors were:

And considering as initial conditions of the process:

Then from (15), (16) and (17), the solution of the DES was defined by the vector in (18).
As a result, the reliability state of each node in the route for each time of unit of the same operation was obtained. By applying this phase of the methodology to each node in the route, a map of the reliability states of all nodes was obtained during all the time of operation

5. Conclusions
The reliability evaluation of routes is a relevant issue in the design of urban freight distribution routes, but some current algorithms and techniques do not consider stages prior to the calculation of reliability. Therefore, combining in one methodology steps of analysis, such as: i) sampling of data; ii) classification of reliability levels; and iii) reliability of each node, enables the input and output information at every stage to being highly correlated with the final result of the methodology. i.e. that the reliability calculation of the route is completely related to the information obtained on the field and its analysis through each phase.
With the methodology here presented, the reliability evaluation of a route of urban freight distribution is simplified, from gathering information of the reliability factors to the evaluation of the route through the application of some algorithm. The methodology also offers the decision maker a useful tool to design and operate complex distribution routes.
Applying the technique of Markov models provides a dynamic analysis, i.e., it enables knowing the behavior of the elements that make up the distribution route at any time unit of operation. And, along with the quantitative measurement of reliability of each node involved in the route, it covers the opportunity area that was observed in different algorithms to evaluate the networks reliability.
Regarding the application, the probability density function (PDF), indicators was defined based on performance goals established for the case here analyzed. Likewise, a reliability approach was considered, based on two variables, which were connectivity and delivery time. The theoretical support for the analysis of reliability through Markov models is also explained, considering it as one of the contributions of this work. While the most important innovation is the use of Markov models, the balanced integration of all phases is important for the effectiveness of the methodology.
However, a key element is to note that the complexity of the methodology lies in the execution of the last phase, where the choice of the algorithm to assess the reliability of the route is at the discretion of the analyst. Consequently, three future works were identified. First, to compare the results of this application with other existing algorithms looking for an exact selection of the algorithm used during the last phase of the method. Second, strengthening the contribution of the first phase with the improvement in the evaluation of probability of transition between states. One option is through bayesian theory, due to the stochastic behavior of the distribution process. And third, standardizing the proposed methodology through the creation of a computer application, which would evaluate the reliability of the route, and design the optimal route based on costs, demands, and reliability.
Acknowledgment
The authors thank Flora Hammer for several useful comments that improved this paper as well as anonymous reviewers for their constructive comments and suggestions.
References
[1] Calderón, K., Se encarece costo de productos por fallas en distribución urbana [En linea]. Noticiero T21 [Consulta: 18 de jun 2012]. Dsiponioble en : http://www.t21.com.mx/news/news_display.php?story_id=14164. [ Links ]
[2] Boudouin, D., Morel, C., and Gardrat, M., Suppy chains and urban logistics plataforms. In Gonzalez-Feliu, J., Semet, F., Routhier, J.L., (eds.), Sustainable urban logistics: Concepts, methods and information systems. Springer, Heideberg, 2014, pp. 01-20. [ Links ]
[3] Crainic, T.G., City logistics. In Chen, Z.L. and Raghavan, S. (eds.), Tutorials in operations research 2008. State-of-the-art decision making Tools in the information-intensive age, INFORMS, 2008, pp. 181-212, [ Links ].
[4] Sanz, G., Pastor, R. and Benedito, E., Distribución urbana de mercancías: Descripción y clasificación de soluciones existentes e implementación de dos soluciones novedosas. DYNA, 80 (179), pp. 6-13, 2013. [ Links ]
[5] Arango-Serna, M.D., Serna-Uran, C.A. and Alvarez-Uribe, K.C., Collaborative autonomous systems in models of urban logistics. DYNA, 79 (172), pp. 171-179, 2012. [ Links ]
[6] Soto-de la Vega, D., Vidal-Vieira, J.G. and Vitor-Toso, E.A., Metodología para la localización de centros de distribución a través de análisis multicriterio y optimización. DYNA, 81 (184), pp. 28-35, 2014. [ Links ]
[7] Arango-Serna, M.D., Adarme-Jaimes, W. and Zapata-Cortes, J.A., Commodities distribution using alternative types of transport. A study in the Colombian Bread SMEs. DYNA ,79 (172), pp. 171-179, 2010. [ Links ]
[8] Galván, D.C., Martínez, L. y Antún, J.P., Prácticas en distribución y su efecto sobre la optimización de la logística urbana. XVI Congreso Panamericano de Transporte, Tráfico y Logística, Lisboa, Portugal, 2010. [ Links ]
[9] Betanzo-Quezada, E., Romero-Navarrete, J. y Obregón-Biosca, S. Un referencial para evaluar la gestión pública en transporte urbano de carga. Gestión y Política Pública, XXII (2), pp. 313-354, 2013. [ Links ]
[10] Morana, J., Sustainable supply chain management in urban logistics. In Gonzalez-Feliu, J., Semet, F., Routhier, J.L. (eds.), Sustainable urban logistics: Concepts, Methods and information systems. Springer, Heideberg, 2014, pp. 21-34. [ Links ]
[11] Arvis, J.F., Alina, M., Ojala, L., Shepherd, B. and Saslavsky, D., The logistics performance index and its indicators. [En línea]. By: World Bank's International Trade Department, 2010, [date of reference December 8 of 2013]. Avaiable at: <http://siteresources.worldbank.org/INTTLF/Resources/LPI2010_for_web. [ Links ]pdf>
[12] Tadashi, Y., Yohe, Y. and Kazuhiro, M., Road network reliability analysis using vehicle routing and scheduling procedures. III International Conference on City Logistics: Logistics Systems for Sustainable Cities, pp. 111-122, 2013. [ Links ]
[13] Robledo, F., Modelos combinatorios de confiabilidad en redes. Apuntes del curso de postgrado Modelos Combinatorios de Confiabilidad en Redes, IMERL/INCO - UdelaR Montevideo, Uruguay, 2009. [ Links ]
[14] Ros, Ll. and Hayes, S., La distribución urbana de mercancías. economistas, vol. 2. Consultores ALTRAN Technologies, pp. 2-4, 2009. [ Links ]
[15] Estrada, R., Análisis de estrategias eficientes en la logística de distribución de paquetería. PhD. Thesis. Universitat Politècnica de Catalunya, Barcelona, Spain, 2007. [ Links ]
[16] García, I.C., Un enfoque metaheurístico para un problema de ruteo con flexibilidad en las fechas de entrega. Ph.D. Thesis, Facultad de Ingeniería Mecánica y Eléctrica, Universidad Autónoma de Nuevo León, México, 2010. [ Links ]
[17] Jenelius, E., Peterson, T. and Mattsson, L.G., Importance and exposure in road network vulnerability analysis. Transportation Research Part A: Policy and Practice, 40 (7), pp. 537-560, 2006. [ Links ]
[18] Susilawai, S., Taylor, M.A.P. and Somenahalli, S.V.C., Travel time reliability measurement for selected corridors in the Adelaide Metropolitan area. Journal of the Eastern Asia Society for Transportation Studies,8, pp. 86-102, 2010. [ Links ]
[19] Husdal, J., Reliability and vulnerability versus cost and benefits. Proceedings of the Second International Symposium on Transportation Network Reliability (INSTR 2004). Christchurch, New Zealand, pp. 182-189, 2004. [ Links ]
[20] Sumper, A., Sudrià, A., Ramírez, R., Villafáfila, R. y Chindris, M., Índices de continuidad en redes de distribución y su mejora. 9° Congreso HISPANO LUSO Ingeniería Eléctrica, pp. 20-24, 2004. [ Links ]
[21] Muñoz, A.Z., Multi-State system reliability design via particle evolutionary swarm optimization. MSc. Thesis, Centro de Investigación en Matemáticas A.C., Guanajuato, México, 2004. [ Links ]
[22] Fuqua, N.B., The applicability of Marvok analysis methods to reliability, maintainability and safety. Selected Topic in Assurance Related Technologies (START), 2 (10), pp. 1-8, 2003. [ Links ]
[23] Rubio, C.T. y Echeverría, A., Modelos de Markov: Una herramienta útil para el análisis fármaco-económico. Pharmacoeconomics -Spanish Research, 3 (2), pp. 71-78, 2006. [ Links ]
[24] Ocaña, R.A., Modelos de Markov aplicados a la investigación en Ciencias de la Salud. Interciencia, 34 (3), pp. 157-162, 2009. [ Links ]
[25] Marín, J.M.D. ,Cadenas de Markov. Apuntes de estadística actuarial II [en linea]. Depto. de Estadística, Univ. Carlos III de Madrid. [date of referenca June 15th of 2013]. Avaiable at: <http://halweb.uc3m.es/esp/Personal/personas/jmmarin/esp/PEst/tema4pe. [ Links ]pdf>
[26] Chin-Chia, J., Performance evaluation of logistics systems under cost and reliability considerations. Transport. Res. Part E, 47 82), pp. 130-137, 2010, doi:10.1016/j.tre.2010.09.012. [ Links ]
M.G. Cedillo-Campos, is a Professor-Researcher in Logistics Systems Dynamics at the Mexican Institute of Transportation (IMT). He is the Founder and President of the Mexican Logistics and Supply Chain Association (AML). Dr. Cedillo-Campos is acknowledged as National Researcher level 1 by the National Council of Science and Technology in Mexico (CONACYT). In 2004, he received a PhD. in Logistics Systems Dynamics from the University of Paris, France. In 2012, he was acknowledged by the Autonomous University of Nuevo Leon (UANL) with the Innovation Award. In 2012, he collaborated as speaker at Georgia Tech Panama. Dr. Cedillo is member of the Mexican Academy of Systems Sciences and the Scientific Chairman of the International Congress on Logistics and Supply Chain (CiLOG) organized by the AML. He is the author of several scientific publications in top journals as Transportation Research Part E: logistics and Transportation Review, Simulation, Computers and Industrial Engineering, Applied Energy, Computers in Industry, Journal of Applied Research and Technology, among others.
J.L. de la Riva-Canizales, is a researcher in industrial engineering at Chrysler. In 2013, he received a MSc in Industrial Engineering from COMIMSA (National Council of Science and Technology), Mexico. He obtained a BSc. degree in Mathematics from the Autonomous University of Coahuila, Mexico. He has worked for logistics businesses in Mexico and as a consultant on supply chain management for global companies, and several Mexican State Governments. His current research interests include quality processes, service operations in supply chains, city logistics, and design of supply chains oriented to emerging markets.
A. Bueno-Solano, heads the Logistics and Multimodal Unit at the Mexican Institute of Transportation (IMT). Dr. Bueno is a founding member of the Mexican Logistics and Supply Chain Association (AML). In 2013, he received a PhD. in Industrial Engineering and Manufacturing Science from COMIMSA (National Council of Science and Technology), Mexico. His PhD. thesis deals with risk propagation modelling in export-oriented supply chains. He has participated as part of important research projects as the first national survey on supply chain security which was supported by the National Council of Science and Technology as well as by the Secretariat of Economy of Mexico. He is the author of several scientific publications in top journals as Transportation Research Part E: logistics and Transportation Review, and Journal of Applied Research and Technology, among others. He is part of the scientific board of the International Congress on Logistics and supply chain (CiLOG) organized by the AML.
J. Gonzalez-Feliu, is a research engineer at the Centre National de la Recherche Scientifique in Lyon, France, and member of the Laboratoire d'Economie des Transports (LET, Laboratory of Transport Economics). He obtained his MSc. degree in Civil Engineering and Urban Planning in 2003 at INSA Lyon (France) and passed his PhD. in Computer and Systems Sciences - Operations Research in 2008 at Politecnico di Torino (Italy). His PhD. thesis deals with urban freight distribution solutions and two-echelon vehicle routing problems. At LET since 2008, his work deals with urban logistics data production, simulation and evaluation, focusing on data collection techniques, simulation of urban routes and shopping trip behaviour, substitution of shopping trips by proximity deliveries, logistics pooling and multi-stage transport systems. His research interests include urban logistics planning and policy, freight demand modeling, scenario assessment, decision support systems, vehicle routing optimization, sustainable supply chain management and collaborative transportation.
J.L. García-Alcaraz, is a Professor-Researcher at the Department of Industrial Engineering at the Autonomous University of Ciudad Juárez in Mexico, a founding member of the Mexican Society of Operations Research and an active member in the Mexican Academy of Engineering. Dr. Garcia is recognized as National Reseracher level 1 by the National Council of Science and Technology in Mexico (CONACYT). He received a MSc. in Industrial Engineering from the Technological Institute of Colima, Mexico, a PhD. in Industrial Engineering from the Tedchnological Institute of Ciudad Juarez, Mexico and a Post-Doctorate at the University of La Rioja, Spain. His main research area are related to modeling and multi-criteria decision-making applied to production processes. He is author and co-author in over 100 articles published in indexed journals and international conferences and congresses as International Journal of Advanced Manufacturing Technology, Expert System with Applications, International Journal of Production Research, Computer in Industry, among others.






















