DOI: http://dx.doi.org/10.15446/dyna.v82n194.49647

Determination of the Rayleigh damping coefficients of steel bristles and clusters of bristles of gutter brushes

Determinación de los coeficientes de amortiguamiento de Rayleigh de cerdas y grupos de cerdas de acero de cepillos laterales

 

Libardo V. Vanegas-Useche ^a, Magd M. Abdel-Wahab ^b & Graham A. Parker ^c

 

^a Facultad de Ingeniería Mecánica, Universidad Tecnológica de Pereira, Pereira, Colombia. lvanegas@utp.edu.co
^b Faculty of Engineering and Architecture, Ghent University, Gent, Belgium. magd.abdelwahab@ugent.be
^c Faculty of Engineering and Physical Sciences, University of Surrey, Surrey, UK. g.parker@surrey.ac.uk

 

Received: March 16^th, 2015. Received in revised form: June 4^th, 2015. Accepted: June 9^th, 2015.

 

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

---

Abstract
Street sweeping is an important service that is usually performed by lorry-type vehicles that have a gutter brush, which is comprised of clusters of steel bristles that sweep the debris found in the road gutter. Effective operation of this brush is important, as most of the debris on roads is located in the gutter. In order to model a gutter brush by means of finite element dynamic analyses, it is necessary to determine appropriate values of the Rayleigh damping coefficients of both individual bristles and clusters of bristles. This paper presents the methodology and results of experimental tests that have been conducted to determine these coefficients. The results obtained are useful when studying the performance of conventional and oscillatory street sweeper gutter brushes by means of dynamic finite element modeling.

Keywords: Rayleigh damping coefficients; bristles of gutter brushes; street sweeping.

Resumen
El barrido de calles es un servicio importante que usualmente se realiza por medio de vehículos tipo camión que tienen un cepillo lateral conformado por grupos de cerdas de acero para barrer la basura que se encuentra en la cuneta de la carretera. Es importante que este cepillo funcione efectivamente, ya que la mayoría de la basura depositada en las carreteras se encuentra en la cuneta. Con el fin de modelar un cepillo lateral mediante análisis dinámico de elementos finitos, es necesario determinar valores apropiados de los coeficientes de amortiguación de Rayleigh tanto de cerdas individuales como de grupos de cerdas. En este trabajo se presenta la metodología y los resultados de pruebas experimentales que se han realizado para determinar estos coeficientes. Los resultados obtenidos son útiles para estudiar el desempeño de los cepillos laterales de las barredoras de calles mediante el modelado dinámico de elementos finitos.

Palabras clave: coeficientes de amortiguamiento de Rayleigh; cerdas de cepillos laterales; barrido de calles.

---

 

1. Introduction

Street sweeping is, in many cases, performed by lorry-type sweepers. There are different types of sweepers [1]; however, they usually comprise a suction unit, a wide broom, and a gutter brush (Fig. 1). There are two basic types of gutter brushes. These differ in the orientation of the bristle rectangular cross section; there are cutting brushes, whose bristles mainly deflect in a brush radial direction, and flicking brushes, whose bristles mainly deflect in a tangential direction. According to Peel et al. [2] and Michielen and Parker [3], around 80% of the debris found on roadways is in the gutter. Therefore, it is of interest to study the behavior and effectiveness of gutter brushes as they have to clear the large amount of debris that is located in the gutter and transfer it to the path of the suction unit or the wide broom.

Despite the relevance of studying gutter brush performance, there are a very limited amount of scientific papers written on the dynamics and performance of gutter brushes; in fact, it seems that research on this topic has only been performed by the Mechatronic Systems and Robotics Research Group at the University of Surrey [4-14]. This research has involved the development and application of mathematical, numerical, and finite element models of gutter brushes, as well as experimental sweeping tests carried out in a gantry test rig. Reviews on this topic have been presented in previous works.

This work is concerned with the development of finite element models of conventional, as well as oscillatory gutter brushes [10]. In order to obtain useful results from the models, suitable values of several parameters have to be obtained, some of them experimentally. This article presents the procedure and results of a number of experimental tests that have been performed to obtain the Rayleigh damping coefficients of both a single bristle and of a cluster of bristles. These parameters, among others, are necessary for the dynamic Finite Element (FE) modeling of gutter brushes. Other parameters that have to be determined are the friction coefficient for bristle-bristle contact [9] and the normal contact stiffness for bristle-surface interaction.

The paper is organized as follows, some basic concepts of damping are introduced in Section 2. The procedure, results, and discussion of experiments for a single bristle are presented in Section 3. Then, the methodology, results, and discussion of experiments for a cluster of bristles are provided in Section 4. Finally, the conclusions are presented in Section 5.

 

2. Background on damping

Damping is the mechanism by which a system's kinetic energy is gradually converted into heat or sound [15]. Due to the reduction in energy, damping has the effect of gradually reducing the system's response, e.g., the displacement amplitude. Thus, in many cases, damping is a beneficial phenomenon without which the system may remain in a state of chaos [16]. There are different sources of damping, e.g., friction between two dry sliding surfaces, fluid resistance, and internal molecular friction. The internal molecular friction is the one that is of interest in this work. It is difficult to determine all the causes of damping in a practical system; therefore, damping is modeled in different ways: viscous damping, Coulomb or dry friction damping, and material or hysteretic damping.

The simplest form of damping is viscous damping, as it leads to linear equations of motion [15]. Because of this, many researchers use viscous damping (e.g., [17-24]). In this type of damping, the damping force is proportional to the velocity of the body. Rayleigh or proportional damping is a form of viscous damping that is proportional to a linear combination of the mass and stiffness dependent damping. Although the physical meaning of this type of damping is not clear, it is a very convenient way to represent damping in numerical models [25]. According to proportional damping:

where C is the damping matrix, M is the mass matrix, K is the stiffness matrix. a_D the mass proportional damping coefficient, and b_D the stiffness proportional damping coefficient are assumed to be constant.

 

3. Rayleigh damping coefficients of a bristle

3.1. Overview

The bristles of a gutter brush, either conventional or oscillatory, deform and vibrate as they make contact, slide, and leave the road surface. During this process, the internal molecular friction in the bristles produces damping. This damping may be taken into account when modeling a gutter brush by means of FE analyses. In the ANSYS® software, this damping can be modeled as Rayleigh damping. In order to determine appropriate damping coefficients, the a_D and b_D of a bristle were subject to experimental tests. The procedure and results of these experiments are presented in Sections 3.2 and 3.3, respectively.

3.2. Methodology

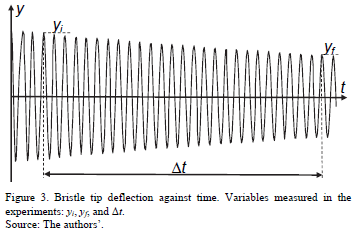
The coefficients a_D and b_D are obtained experimentally, by analyzing the vibration amplitudes of steel bristles in cantilever's rate of decay. The experimental setup is shown in Fig. 2. The bristles were supported rigidly in a heavy clamping device, so that the damping associated with the clamping system is negligible. Free vibrations were produced by displacing the tip of the bristle downwards and then releasing it. It is assumed that the vibration of the bristle is dominated by the first mode. Therefore, the beam of infinite Degrees of Freedom (DOFs) is assumed to be equivalent to a single DOF system with viscous damping, and it is characterized by the motion of the free end. A measuring scale at the bristle tip enabled the decay of the vibration amplitudes to be tracked. The time Dt required for the deflection amplitude, y_max, to reduce from a certain value, y_i, to another value, y_f, (Fig. 3) was recorded three times, and the average was taken. This procedure was repeated for several pairs of values (y_i, y_f) and for three bristles (A, B, and C) of different lengths. The lengths and the first natural frequencies of the bristles are l_bA = 481 mm, l_bB = 240 mm, l_bC = 95.8 mm, f_A = 1.89 Hz, f_B = 7.22 Hz, and f_C = 45.3 Hz. The cross section of the bristles is 0.5 × 2 mm². The constants a_D and b_D are determined from a best fit of the experimental data. It should be noted that it was not possible to use signal analysis. This is because the wire that transmits the signal from the accelerometer generates a much higher level of damping than the bristles themselves.

The number of cycles during the time Dt is estimated by:

Where f is the frequency of bristle vibration. The frequency of bristle A was obtained experimentally, as it is small, and, therefore, corresponds to f_Ad, which is called the frequency of damped vibration. f_Ad = 1.891 Hz ± 0.009 Hz (standard error). The value of f_B and f_C given previously are the theoretical first natural frequencies. However, as [15]:

and, it is anticipated that the damping ratio of the bristles, z_D, is small, and that the first natural frequency, f_i (i = 1), and the frequency of damped vibration, f_d, do not differ greatly. Hence, the natural frequencies may be used to estimate N_c (from eq. 2).

The logarithmic decrement, d, which represents the rate at which the amplitude of free damped vibration decreases, may be expressed as [15]:

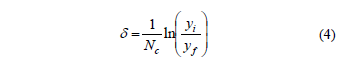
The damping ratio is defined as the ratio of the damping constant (or viscous damping coefficient ), c, to the critical damping constant, c_c:

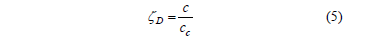
and it is given by [15]:

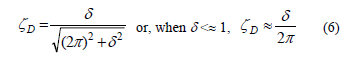
Thus, from the measured values y_i, y_f, and Dt and the experimental or theoretical frequency, f, the damping ratio for each bristle can be calculated by using eq. (2), (4), (6).

For each bristle, the experimental data were used to obtain a y_max - t curve. The experimental points (t, y_max) were fitted to a curve. Logarithmic, power, and exponential functions were considered. In general, the power equation provided the best fit, and it was selected, even though all the lines produced very similar results.

3.3. Results and discussion

Fig. 4 presents the experimental data and the trend lines for the three bristles. The time t_offset is an offset obtained from the regression analyses. The logarithmic decrement, d, and damping ratio, z_D, are, in theory, constant for a free viscously damped vibrating system. However, the experimental results suggest that they depend on the deflection amplitude, y_max. The trends in Fig. 4 indicate that d and z_D are larger for higher values of y_max. However, for the longest bristle (l_bA = 481 mm, for which f_A = 1.89 Hz), d and z_D are almost constant for the different amplitudes. The dependence of d and z_D on the vibration amplitude may be partly due to the fact that the air resistance to which the bristles are subjected is proportional to the velocity raised to a power greater than 1. Higher deflections produce higher bristle speeds and, consequently, much higher aerodynamic forces. For each bristle, damping ratios for four values of y_max were calculated using the respective trend lines. These values are shown in the z_D - f curve in Fig. 5.

The damping ratio is related to the Rayleigh damping coefficients by [26]:

where w_i is a given angular frequency, and z_Di, a_Di, and b_Di are the values for that frequency.

In the ANSYS® software, only a value of each a_Di and b_Di can be input in a load step, regardless of the frequencies that are active in that load step. In this work, it is assumed that a_D = a_Di and b_D = b_Di are constant coefficients, i.e., they are independent of the frequency. This is not entirely satisfactory, but provided that the frequencies excited lie in a small range, acceptable results may be obtained.

Eq. (7) can be rearranged as follows:

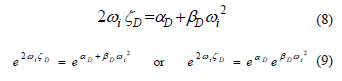
Eq. (9) is of the form:

Hence, the data points in Fig. 5 can be fitted to an exponential equation. The regression analysis yields the values a_D = 0.104 s^-1 » 0.1 s^-1 and b_D = 1.07´10^-5 s » 0.01 ms. The z_D - f curve that corresponds to these values is also shown in Fig. 5. Lastly, these values were used in a FE analysis for the free damped vibration of a cantilever beam as a means of verification. For l_b = 95.8 mm, y_i = 10 mm, and y_f = 5 mm, the damping ratios from eq. (7) and from the logarithmic decrement obtained from the FE results are 0.001599 and 0.001595, respectively (0.3% difference). This result seems satisfactory.

The mass component of Rayleigh damping (a_DM) damps rigid body motion [26], i.e., it is associated with the damping of inertial movements. Thus, it may be used when a structure is affected by fluid drag [27]. The bristles of a gutter brush, as well as those used in the experiments, are subjected to aerodynamic effects. Then, some mass proportional damping is expected. The bristles are also subjected to internal friction, which may be associated with stiffness proportional damping (b_DK). The results of the experiments suggest that a_D and b_D can be assumed to be constant for a certain range of frequencies and equal to a_D » 0.1 s^-1 and b_D » 0.01 ms. Although this is a simplification, hereinafter, the mass component of damping will be associated with aerodynamic effects and the stiffness component with internal friction (of a bristle or a cluster).

 

4. Rayleigh damping coefficients of a cluster

4.1. Overview

The modeling of an oscillatory gutter brush may be very complex. The bristles operate in non-steady state conditions, making contact with the surface, debris, neighboring bristles, and, possibly, bristles in other clusters. Thus, the bristles in a cluster should be modeled by several beams. However, the computational resources needed are huge. Consequently, it is of interest to model a cluster with a single beam. In order to do this, it is necessary to determine equivalent values of the damping coefficients of a cluster. These will take the internal friction into consideration in each bristle, as well as the energy dissipation caused by the interaction among bristles.

Experiments were carried out to estimate suitable values of a_D and b_D, to model a cluster of bristles as a single beam in a FE model. This was necessary because the computational resources needed to model the whole cluster, or even a small number of bristles per cluster, exceed the available resources by far. For example, a single 1 s simulation of a cluster of only five bristles may take about 20 days on an available PC.

4.2. Methodology

Several clusters of a number of brushes with steel bristles of different lengths were used. The cross section of the bristles is 0.5 × 2 mm². An initial deformation was applied to every cluster by deflecting the bristle tips an arbitrary amount. The cluster was then released so that the bristles withstood free damped vibrations. Due to the characteristics of the initial deformation and the interaction among bristles, the first mode is the dominant. Hence, the cluster is treated as a single DOF system characterized by the deflection of the tips. As the cluster oscillates, adjacent bristles slide on one another, generating friction forces, and they may also collide. Due to these interactions, the vibration amplitudes of a cluster's rate of decay tends to be much greater than its counterpart of a single bristle. However, a small fraction of the bristles are apart from other bristles, and the rate of decay of their vibrations is similar to that found in Section 3.

Due to the rapid decay, the procedure for a single bristle cannot be used reliably in this case. For this reason, a digital camera that captures 25 frames per second (fps) was used to capture the images of the vibrating cluster. In this way, the variation of the deflections with time could be obtained. As the bristles of a cluster are not tightly arranged but are dispersed at different angles, every bristle tip has its own decay of vibration amplitudes. A suitable bristle or part of the cluster was selected for each cluster to track its tip deflections. A measuring scale was used for this purpose. Also, a stopwatch was used to verify the number of fps recorded by the camera. Then, the recorded images were analyzed frame by frame, and approximate values of deflection were written down for a number of time points. Fig. 6 shows one of the setups that was prepared for one of the experiments.

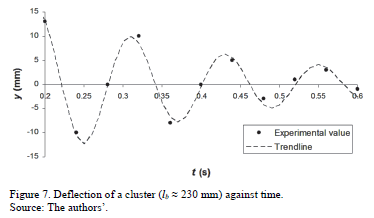
Fig. 7 shows, as an example, the experimental points obtained from the images of one of the experiments. The "best" fit of the experimental points, which is obtained as described in the following paragraphs, is also shown.

To obtain the logarithmic decrement, d, the damping ratio, z_D, and the damping coefficients, a_D and b_D, it is necessary to fit the experimental points to a curve. The displacement of a single DOF underdamped system with viscous damper is given by [15]:

where y₀ and t_i are the initial displacement and velocity (t = 0), respectively. It is anticipated that for all the results obtained z_D is very small (z_D < 0.09). Taking this into account and by using the approximation in eq. (6), eq. (11) may be simplified:

where y_i and t_i are constant values that are obtained from the experimental data. This equation has four parameters: y_i, t_i, f_i, and d. To obtain a suitable value of the logarithmic decrement, d, it is necessary to test a large number of combinations of these four variables. After the required number of iterations, a value of d is selected, and the damping ratio is calculated (eq. 6). The selected value of d is the one that produces the minimum sum of the squared differences between the curve and the experimental points.

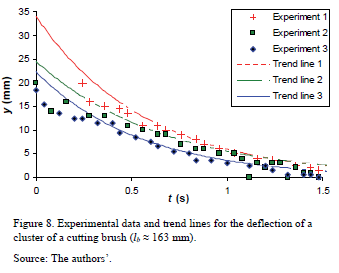
The procedure described in the preceding paragraph is suitable when the frequency is sufficiently small, e.g., when l_b >» 220 mm. This is because the camera is capable of recording enough frames to obtain a curve like the one shown in Fig. 7. For clusters of shorter bristles, the frequency of oscillation is higher, and the determination of the y - t curve becomes more difficult, unless a camera with better control of the shutter speed and more fps were available. In view of this, for most of the brushes tested, a less accurate method of obtaining d was used. The frames recorded were used to estimate the extreme positions of a certain part of the cluster. These deflection values were written down. As an example, Fig. 8 presents the experimental points for clusters of a cutting brush; the brush was tested three times. Eq. (13) was used to fit the experimental data by visual observation:

The trend lines obtained with eq. (13) constitute upper bounds of the experimental points. Fig. 8 also shows the curves that seem to best fit the experimental data.

4.3. Results and discussion

For each of the five brushes tested, values of d and z_D were obtained from at least three experiments. Table 1 presents the summary of the results. It should be noted that, to the authors' best knowledge, this is the first investigation into the damping of gutter brushes' steel bristles. It is of interest to note that the estimated frequencies of the brush in row 1 are higher than the theoretical natural frequency. This may be partly due to the propagation of impacts among bristles. They are initially dispersed, but the initial deformation forces the bristles to become close to each other. When the bristles are released, they tend to withstand vibrations with different amplitudes, generating wave propagations.

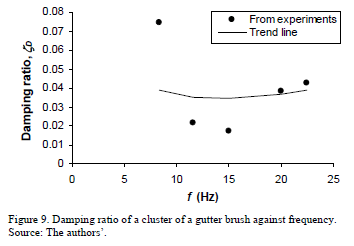
The points (f, z_D) are shown in Fig. 9. Similar to the case of the single-bristle experiments, it is assumed that the damping coefficients, a_D and b_D, are independent of the frequency. Hence, the data points are also fitted through an exponential equation (eq. 10). The regression analysis yields the values of the damping coefficients: a_D = 3.01 s^-1 » 3 s^-1 and b_D = 0.396 ms » 0.4 ms. The z_D - f curve shown in Fig. 9 corresponds to these values. Taking into account the results and discussion in Section 3.3, for the case of single bristles, these results seem appropriate. These values are not accurate, as can be seen from the high dispersion of the experimental data. The dispersion is very high partly because, contrary to what has been assumed, the damping coefficients are not independent of the frequency. Damping coefficients also vary from one particular brush to another, from one particular cluster to another, and during brush life. Regarding the brush life, new brushes tend to have clusters with closely packed bristles, whereas used brushes tend to have clusters with bristles presenting high dispersion. All of this affects the way the vibrations are damped.

To conclude, due to its inherent complexities, damping is a physical phenomenon that has been dealt with by using equations that may not represent the reality. The determination of an accurate, unsophisticated model for the damping of the clusters of gutter brushes seems to be a very difficult task, if not impossible. Damping in a cluster is produced by aerodynamic forces, internal friction in the bristles, and the interaction among bristles. In addition, the characteristics of the clusters vary from one to another, e.g., each cluster may have a different number of bristles, and they are arranged in a different fashion, depending on the clamping conditions and the use to which they have been subjected. Due to the complexities involved in modeling damping, the damping coefficients determined from the experimental tests (both for clusters and for bristles) are rough estimates. However, the use of these values in FE analyses may provide a practical insight into the quantitative performance of oscillatory and non-oscillatory gutter brushes. Lastly, from an analysis of Newton's second law and eq. (1), it is concluded that the damping coefficients of a cluster can be used directly in a FE model of a gutter brush when the cluster is modeled with a single beam.

 

5. Conclusions

This article presented the methodology and results of experimental tests, as well as the accompanying FE analyses, to determine the Rayleigh damping coefficients of the bristles and clusters of gutter brushes used for road sweeping. In numerical analyses, damping is usually modeled as Rayleigh damping, in which the damping matrix is a linear combination of mass and stiffness dependent damping. The damping constants were obtained by subjecting bristles and clusters in cantilever to free damped vibrations. These were treated as single degree of freedom systems characterized by the motion of the tips. The results suggest that the damping coefficients of a bristle may be taken as a_D = 0.1 s^-1 and b_D = 0.01 ms, and those of a cluster as a_D = 3 s^-1 and b_D = 0.4 ms. Due to the complexities of the vibration of clusters of gutter brushes, the determined values of a_D and b_D are only estimates of the mean values; they may greatly vary depending on the arrangement of each particular cluster and the frequency of oscillation, among others aspects.

 

Acknowledgements

The authors acknowledge the support of the Universidad Tecnológica de Pereira (Colombia), the University of Surrey (UK), and the Programme Alban, European Union Programme of High Level Scholarships for Latin America, identification number (E03D04976CO).

 

References

[1] Vanegas-Useche, L.V. y Parker, G.A., Barrido de calles y vehículos barredores. Scientia et Technica, [Online] 26, pp. 85-90, 2004. Available at: http://www.redalyc.org/articulo.oa?id=84911640015        [ Links ]

[2] Peel, G., Michielen, M. and Parker, G., Some aspects of road sweeping vehicle automation, Proc. 2001 IEEE/ASME Int. Conf. Adv. Intelligent Mechatronics, I-II, pp. 337-342, 2001. DOI: 10.1109/AIM. 2001.936477        [ Links ]

[3] Michielen, M. and Parker, G.A., Detecting debris using forward looking sensors mounted on road sweeping vehicles, Proc. of Mechatronics 2000, paper number: M2000-094, 2000.         [ Links ]

[4] Vanegas-Useche, L.V., Abdel-Wahab, M.M. and Parker, G.A., Effectiveness of gutter brushes in removing street sweeping waste. Waste Management, 30(2), pp. 174-184, 2010. DOI: 10.1016/j. wasman.2009.09.036        [ Links ]

[5] Vanegas-Useche, L.V., Abdel-Wahab, M.M. and Parker, G.A., Modeling of an oscillatory freely-rotating cutting brush for street sweeping. DYNA, [Online] 78(170), pp. 204-213, 2011. Available at: http://www.revistas.unal.edu.co/index.php/dyna/article/view/29504/48793        [ Links ]

[6] Vanegas-Useche, L.V., Abdel-Wahab, M.M. and Parker, G.A., Dynamics of a freely rotating cutting brush subjected to variable speed. International Journal of Mechanical Sciences, 50(4), pp. 804-816, 2008. DOI: 10.1016/j.ijmecsci.2007.11.004        [ Links ]

[7] Vanegas-Useche, L.V., Abdel-Wahab, M.M. and Parker, G.A., Dynamics of an unconstrained oscillatory flicking brush for road sweeping. Journal of Sound and Vibration, 307(3-5), pp. 778-801, 2007. DOI: org/10.1016/j.jsv.2007.07.010        [ Links ]

[8] Peel, G.A general theory for channel brush design for street sweeping, PhD. Thesis, University of Surrey, Guilford, UK, [Online]. 2002. Available at: http://epubs.surrey.ac.uk/792198/        [ Links ]

[9] Vanegas-Useche, L.V., Abdel-Wahab, M.M. and Parker, G.A., Determination of friction coefficients, brush contact arcs, and brush penetrations for gutter brush-road interaction through FEM. Acta Mechanica, 221(1-2), pp. 119-132, 2011. DOI: 10.1007/s00707-011-0490-2        [ Links ]

[10] Vanegas-Useche, L.V., Abdel-Wahab, M.M. and Parker, G.A., Dynamic finite element model of oscillatory brushes. Finite Elements in Analysis and Design, 47, pp. 771-783, 2011. DOI: org/10.1016/j. finel.2011.02.008        [ Links ]

[11] Wang, C., Brush modelling and control techniques for automatic debris removal during road sweeping, PhD. Thesis, University of Surrey, Guilford, UK, [Online] 2005. Available at: http://ethos.bl.uk/OrderDetails.do?uin=uk.bl.ethos.421309        [ Links ]

[12] Abdel-Wahab, M., Parker, G. and Wang, C., Modelling rotary sweeping brushes and analyzing brush characteristic using finite element method. Finite Elements Ana. Des., 43(6-7), pp. 521-532, 2007. DOI: 10. 1016/j.finel.2006.12.003        [ Links ]

[13] Abdel-Wahab, M.M., Wang, C., Vanegas-Useche, L.V. and Parker, G., Experimental determination of optimum gutter brush parameters and road sweeping criteria for different types of waste. Waste Management, 31, pp. 1109-1120, 2011. DOI: 10.1016/j.wasman.2010.12.014        [ Links ]

[14] Vanegas-Useche, L.V., Abdel-Wahab, M.M. and Parker, G., Effectiveness of oscillatory gutter brushes in removing street sweeping waste. Waste Management, In Press, Corrected Proof, 2015. DOI: 10.1016/j.wasman.2015.05.014        [ Links ]

[15] Rao, S.S., Mechanical Vibrations, fourth edition. New Jersey: Pearson Education, Inc., 2004.         [ Links ]

[16] Puthanpurayil, A.M., Dhakal, R.P. and Carr, A.J., Modelling of in-structure damping: a review of the state-of-the-art, Proc. Ninth Pacific Conf. Earthquake Engineering, [Online]. Paper Number 091, 2011. Available at: http://db.nzsee.org.nz/2011/091.pdf        [ Links ]

[17] Ríos-Gutiérrez, M. and Silva-Navarro, G., Control activo de vibraciones en estructuras tipo edificio usando actuadores piezoeléctricos y retroalimentación positiva de la aceleración. DYNA, [Online]. 80(179), pp. 116-125, 2013. Available at: http://www.revistas.unal.edu.co/index.php/dyna/article/view/30733/html_33        [ Links ]

[18] Carrillo, J., González, G. and Llano, L., Evaluation of mass-rig systems for shaking table experiments. DYNA, [Online]. 79(176), pp. 159-167, 2012. Available at: http://www.revistas.unal.edu.co/index.php/dyna/article/view/28509/43559        [ Links ]

[19] Gómez-Pizano, D., Comparison of frequency response and neural network techniques for system identification of an actively controlled structure. DYNA, [Online]. 78 (170), pp. 79-89, 2011. Available at: http://www.revistas.unal.edu.co/index.php/dyna/article/view/29390/48778        [ Links ]

[20] Valencia de Oro, A.L., Ramírez, J.M., Gómez, D. y Thomson, P., Aplicación interactiva para la educación en dinámica estructural. DYNA, [Online]. 78(165), pp. 72-83, 2011. Available at: http://www.revistas.unal.edu.co/index.php/dyna/article/view/25641/39139        [ Links ]

[21] Hurtado-Cortés, L. y Villarreal-López, L., Control robusto de un sistema mecánico simple mediante una herramienta gráfica. DYNA, [Online]. 77(162), pp. 214-223, 2010. Available at: http://www.revistas.unal.edu.co/index.php/dyna/article/view/15852/36191        [ Links ]

[22] Gómez, D., Marulanda, J. and Thomson, P., Sistemas de control para la protección de estructuras civiles sometidas a cargas dinámicas. DYNA, [Online]. 75 (155), pp. 77-89, 2008. Available at: http://www.redalyc.org/articulo.oa?id=49611953009        [ Links ]

[23] Carrillo, J., Alcocer, S.M. and Gonzalez, G., Experimental assessment of damping factors in concrete housing walls. Ingeniería e Investigación, [Online]. 32(3), pp. 42-46, 2012. Available at: http://www.revistas.unal.edu.co/index.php/ingeinv/article/view/35939/37232        [ Links ]

[24] Bedoya-Ruiz, D., Ortiz, G.A. and álvarez, D.A., Behavior of precast ferrocement thin walls under cyclic loading: an experimental and analytical study. Ingeniería e Investigación, [Online]. 34(1), pp. 29-35, 2013. Available at: http://www.revistas.unal.edu.co/index.php/ingeinv/article/view/40420/44456        [ Links ]

[25] Semblat, J.F., Rheological interpretation of Rayleigh damping. Journal of Sound and Vibration, [Online]. 206(5), pp. 741-744, 1997. Available at: http://arxiv.org/ftp/arxiv/papers/0901/0901.3717.pdf        [ Links ]

[26] SAS IP, Inc. Release 10.0 Documentation for ANSYS, 2005.         [ Links ]

[27] NAFEMS, Earthquake rocking [Online]. 2004 [date of reference 2006]. Available at: http://www.nafems.org/publications/downloads/benchmark/october_2004/earthquake_rocking.pdf.         [ Links ]

 

L.V. Vanegas-Useche, is a professor in the Mechanical Engineering Department at the Universidad Tecnológica de Pereira, Colombia. He received his BSc. in Mechanical Engineering in 1994, from the Universidad Tecnológica de Pereira, Pereira, Colombia, his MSc. in Advanced Manufacturing Technology and Systems Management in 1999, from the University of Manchester, Manchester, UK, and his PhD. in Mechanical Engineering in 2008, from the University of Surrey, Guildford, UK. He has published more than 50 scientific papers. His research interests include: Fracture Mechanics, Fatigue, Mechanical Design, and Finite Element Modeling of Machine Elements and Structures. ORCID: 0000-0002-5891-8696

M.M. Abdel-Wahab, is a professor of applied mechanics at the Department of Mechanical Construction and Production at Ghent University, Belgium. He received his BSc. in1988, in Civil Engineering and his MSc. in1991, the Structural Mechanics, all of them from Cairo University. He completed his PhD. in Fracture Mechanics in 1995 at KU Leuven, Belgium. He was awarded his Dr. from the University of Surrey in 2008. He has published more than 200 scientific papers on Solid Mechanics and Dynamics of Structures. His research interests include Finite Element Analysis, Fracture Mechanics, Damage Mechanics, Fatigue of Materials, Durability, and Dynamics and Vibration. ORCID: 0000-0002-3610-865X

G.A. Parker, is emeritus professor of Mechanical Engineering at the Department of Mechanical and Physical Sciences at the University of Surrey. He holds the following qualifications and titles: BSc., PhD., FIMechE, MEM.ASME, CEng, and Eur.Ing. He is also member of the EPSRC Mechanical Engineering College. His research interests include Virtual and Augmented Reality, Control and Systems Integration, Machine Vision, Brushing Technology, and Fluid Control Systems. ORCID: 0000-0003-0677-6451