DOI: http://dx.doi.org/10.15446/dyna.v83n196.48031

Numerical experimentation for the optimal design of reinforced rectangular concrete beams for singly reinforced sections

Experimentación numérica para el diseño óptimo de vigas rectangulares de concreto reforzado para secciones simplemente reforzadas

 

Arnulfo Luevanos-Rojas

 

Juarez University of the State of Durango, Gómez Palacio, Durango, Mexico. arnulfol_2007@hotmail.com

 

Received: December 26^th, 2014. Received in revised form: August 1^rd, 2015. Accepted: March 10^th, 2016.

 

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

---

Abstract
This paper presents a model for the optimal design of reinforced rectangular concrete beams for singly reinforced sections. It develops an analytical approach to the problem, based on a criterion of minimum cost and minimum weight design with a reduced number of design variables. Representative examples are presented to illustrate the applicability of the formulation in accordance with building code requirements for structural concrete (ACI 318S-13), including the comments on the standards. A comparison is made between the optimal design solution and current design practice for reinforced rectangular concrete beams. The optimal solution for the design of reinforced rectangular concrete beams shows clearly that significant savings can be made in the costs of the construction materials used - i.e. reinforcement steel and concrete. In addition, the problem formulation can be applied using a nonlinear mathematical programming format.

Keywords: optimal design; minimum cost design; minimum weight design; reinforced rectangular concrete beams; singly reinforced sections.

Resumen
En este trabajo se presenta un modelo para el diseño óptimo de vigas rectangulares de concreto armado para secciones simplemente reforzadas. Un enfoque analítico del problema basado en un criterio de diseño de costo mínimo y diseño de peso mínimo con un número reducido de variables de diseño se desarrollan. Ejemplos típicos se presentan para ilustrar la aplicabilidad de la formulación de acuerdo con los códigos de construcción de concreto estructural (ACI 318S-13) y los comentarios. Una comparación se hace entre la solución del diseño óptimo y la práctica del diseño actual de vigas rectangulares de concreto armado. La solución óptima para el diseño de vigas rectangulares de concreto armado muestra claramente que los ahorros significativos se pueden hacer en los costos de los materiales de construcción utilizados para la fabricación de vigas como son el acero de refuerzo y concreto. Además, la formulación del problema se puede aplicar en un formato de programación matemática no lineal.

Palabras clave: diseño optimo; diseño de costo mínimo; diseño de peso mínimo; vigas rectangulares de concreto reforzado; secciones simplemente reforzadas.

---

 

1. Introduction

Structural design requires judgment, intuition and experience, in addition to the ability to design structures that are safe, serviceable and economical. Design codes do not necessarily produce designs that satisfy all of these conditions [1].

Structural design is an iterative process. The initial design is the first step in the process. Though the various aspects of structural design are controlled by many codes and regulations, structural engineers must exercise caution and use their judgment, as well as getting their calculations right, if they are to interpret the various provisions of the code in a manner that produces efficient and economically rational designs [2].

The optimum design of structures has been the topic of a large number of studies in the field of structural design. A designer's goal is to develop an "optimal solution" for the structural design under consideration. This normally implies the most economic structure that does not impair the functional purposes the structure is intended to satisfy [3].

An optimum design is generally considered to be the one design that best satisfies the criteria for the project. Typically there is some kind of objective function that can be computed from the variables that define a design. The value of the objective function is used to compare feasible designs and to determine the "best" or "optimum" design [4].

In structural engineering, the objective statement can also be put in the form of an objective function. Some typical objective statements, and their associated objective functions are:

In structural design, design constraints are frequently referred to as LIMIT STATES. Limit States are conditions of potential failure, where failure is defined as any state that makes the design infeasible (i.e., it will not work for its intended purpose) [4,5].

Limit states take the general form of:

Demand < Capacity

Structural limit states tend to fall into two major categories: strength and serviceability [4,5].

1) Strength Limit States

Strength-based limit states are potential modes of structural failure. For steel members, the failure may mean either yielding (permanent deformation) or rupture (actual fracture). The strength-based limit state may be written in the general form:

Required Strength < Nominal Strength

Required strength is the internal force derived from the analysis of the structure being designed. For example, when designing a beam, required strength is the maximum moment, M, computed for the beam. Nominal strength is the predicted capacity of the beam, for example in bending; it is the maximum moment, M_n, that the beam is capable of supporting (a function of the stress capacity of the material and the section properties of the member) [4,5].

Typically, structural design specifications use the following variables to denote the different strengths:

P = Axial Force
M = Bending Moment
V = Shear Force
R = Reaction Force

2) Serviceability Limit States

Serviceability limit states are conditions that are not strength-based but may still make a structure unsuitable for its intended use. The most common serviceability limit states in structural design are deflection, vibration, slenderness and clearance. Serviceability limit states may be written in the general form:

Actual Behavior < Allowable Behavior

An example is deflection. A loaded cantilever beam will display deflection at the free end (actual behavior) that must be kept lower than allowable deflection (allowable behavior) [4,5].

Serviceability limit states tend to be less rigid requirements than strength-based limit states, as the safety of the structure is not in question. Serviceability limit states don't tend to put people's lives at risk nor do they risk property damage [4,5].

It is worth noting that some engineers find it useful to divide the left side of limit state inequalities by the right, as follows:

(Required Strength/Nominal Strength) < 1.00

(Actual Behavior)/(Allowable Behavior) < 1.00

This is useful for two reasons. It makes comparison easier (the resulting value must be < 1.00) and the resulting number provides information on the percentage of capacity used. Knowing the percentage of capacity makes it easier to decide which limit states are critical as work progresses on optimizing a complex design problem.

The best solution is the one that returns the section with the best objective function value [4,5].

The titles of some papers that discuss the use of optimization methods are: "Validación de soluciones obtenidas para el problema del despacho hidrotérmico de mínimo costo empleando la programación lineal binaria mixta" [6]; "Route optimization of urban public transportation" [7];"Methodology for distribution centers location through multicriteria analysis and optimization" [8]; and "Multiobjective optimization of the reactive power compensation in electric distribution systems" [9].

The optimization of building structures is a prime goal of designers and has been investigated by many researchers in the past, in papers such as: "Optimum Design of Unstiffened Built-up Girders" [10]; "Shape Optimization of RC Flexural Members" [11]; "Sensitivity Analysis and Optimum Design Curves for the Minimum Cost Design of Singly and Doubly Reinforced Concrete Beams" [12]; "Optimal Design of a Welded I-Section Frame Using Four Conceptually Different Optimization Algorithms" [13]; "New Approach to Optimization of Reinforced Concrete Beams, Computer and Structures" [14]; "Cost Optimization of Singly and Doubly Reinforced Concrete Beams with EC2-2001" [15]; "Cost Optimization of Reinforced Concrete Flat Slab Buildings" [16]; "Multi Objective Optimization for Performance-Based Design of Reinforced Concrete Frames" [17]; "Design of Optimally Reinforced RC Beam, Column, and Wall Sections" [18]; "Cost Optimization Of Doubly Reinforced Rectangular Beam Section" [3].

Artificial Neural Networks (ANNs) have been used in the field design of concrete structure , the most important results being achieved in the structural design process and structural analysis. Relevant papers here are: "Modelling Confinement Efficiency of Reinforced Concrete Columns with Rectilinear Transverse Steel using Artificial Neural Network" [19]; "Simulating Size Effect on Shear Strength of RC Beams without Stirrups using Neural Networks" [20]; "Neural Network Evaluation of Steel Beam Patch Load Capacity" [21]; "Damage Assessment in Structure From Changes in Static Parameter using Neural Networks" [22]; "Genetically optimized artificial neural network based optimum design of singly and doubly reinforced concrete beams" [1]; "Optimum Design of Singly and Doubly Reinforced Concrete Rectangular Beam Sections: Artificial Neural Networks Application" [2]. The ANN models built by these researchers basically establish the structural parameters of the inputs to the ANN model, such as material properties, boundary conditions and the size of the structure in question, in order to predict its ability to resist the load for which it is designed [2,23].

Optimization is highly linked to the selection of the most suitable structural system, sized to ensure the least overall cost. In structural design, many parameters are incremental in nature, rendering a continuous approach almost impossible to implement in any given practical optimization exercise [2,24].

This paper presents a model for achieving optimal design of reinforced rectangular concrete beams for singly reinforced sections. It develops an analytical approach to the problem, based on a criterion of minimum cost and minimum weight design with a reduced number of design variables. Representative examples are presented to illustrate the applicability of the formulation in according with building code requirements for structural concrete (ACI 318-13), including the comments on the standards. A comparison is made between the optimal design solution and current design practice for reinforced rectangular concrete beams. The optimal solution for design of reinforced rectangular concrete beams clearly shows that significant savings can be made in the costs of the materials used for their fabrication, that is, reinforcement steel and concrete.

 

2. Methodology

2.1. Optimization technique

With optimization problems the goal is to minimize the weight, volume or cost of the structure under certain deterministic behavioral constraints. The mathematical formulation of a typical structural optimization problem with respect to the design variables and objective and constraint functions can be expressed in standard mathematical terms as a nonlinear programming problem as follows [6-9,25-28]:

subject to

where: x is the vector of design variables, F(x₁, x₂… x_n) is the objective function to be minimized, h_j(x) is the behavioral constraint, and x_i^k and x_i^sare the lower and the upper bounds of typical design variable x_i.

2.2. Problem formulation

The goal of optimization is to find the best solution amongst a set of candidate solutions, using efficient quantitative methods. In beam design, the decision variables represent the quantities to be determined, and a set of decision variable values constitutes a candidate solution. An objective function, which is either maximized or minimized, expresses the goal, or performance criterion, in terms of decision variables. The set of allowable solutions and, hence, the objective function value, is constrained by factors that govern the beam design.

Fig. 1 shows the geometry of a typical single reinforced rectangular section with a simplified rectangular stress block, as provided in the ACI Code [29-31].

The following factors are defined for a given problem:

where: h is total depth, d is effective depth, and r is coating.

In eq. (2), h (the geometric property) is a function of the effective depth, d is variable, and the coating r is constant.

When a rectangular beam section is designed, the nominal bending moment M_n, with a cross section width b or effective depth d, and material properties f'_c and f_y are generally given.

The equations given in the ACI Code [29-31] are:

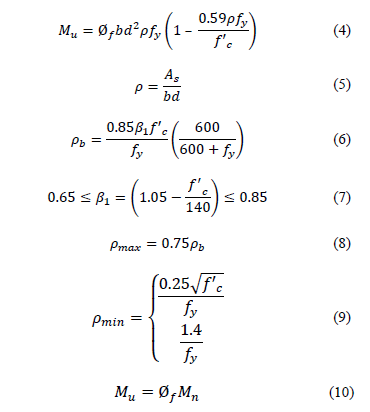
where: M_u is the factored maximum moment, Ø_fis the strength reduction factor by bending, with value 0.90, r is ratio of A_sto bd, b₁is the factor relating the depth of the equivalent rectangular compressive stress block to neutral axis depth, f_y is the specified yield strength of reinforcement of steel, f'_c is the specified compressive strength of concrete at 28 days, and M_n is the nominal bending moment.

2.2.1.1. Objective function: cost minimization

A cost function is defined as the total cost C_t, which is equal to the cost of flexural reinforcement C_s, plus the cost of concrete, C_c. These costs involve material and fabrication costs, respectively. The costs refer to the unit costs of reinforcement steel and concrete for a given unit volume. The cost of the beam of a unit length is:

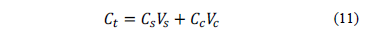
where: V_s is volume of reinforcement steel and V_c is volume of concrete per unit length of beam. These equations are:

Substituting eq. (12) and (13) into eq. (11) produces the following equation:

If we consider a = C_s /C_c and this is substituted into eq. (14) produces the following equation:

2.2.1. Case 1

Assuming that the constant parameters are: M_u, b, f'_c and f_y

then the design variables are: r, A_s and d.

The objective function to minimize is:

subject to:

2.2.1.2. Case 2

Now assume that the constant parameters are: M_u, d, f'_c and f_y.

The design variables are: r, A_sand b.

The objective function to minimize is:

subject to:

2.2.2. Objective: function to minimize the weight

A weight function is defined as total weight, W_t, which is equal to the weight of flexural reinforcement, W_s, plus the weight of concrete, W_c. These weights record only the weight of materials; they refer to the unit weights of reinforcement steel and concrete for a given unit volume. The weight of the beam of a unit length is:

Substituting eq. (12) and (13) into eq. (26) produces:

If we consider g = W_s/W_c and it is substituted into eq. (27) the result is as follows:

2.2.2.1. Case 3

Now assume that the constant parameters are: M_u, b, f'_cand f_y.

The design variables are: r, A_s and d.

The objective function to minimize is:

subject to:

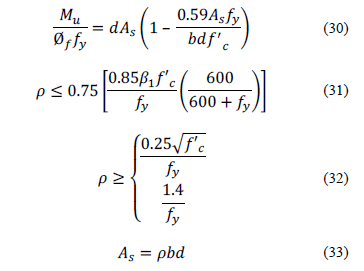
2.2.2.2. Case 4

Now assume that the constant parameters are: M_u, d, f'_c and f_y.

The design variables are: r, A_s and b.

The objective function to minimize is:

subject to:

MAPLE 14 software, designed to solve the optimization problem, was used to assess the optimal design with respect to minimum cost and minimum weight of reinforced rectangular concrete beams for singly reinforced sections.

 

3. Numerical Problems

3.1. Case Example 1

A rectangular beam section with b = 30 cm is given. Values must be determined for the optimum ratio of the reinforcement steel, r, its optimum area, A_s, and the optimum effective depth, d, for M_u = 700 kN-m, f'_c = 28 MPa and f_y = 420 MPa. It is assumed that r = 4 cm, and the ratio of reinforcement steel cost to concrete cost is: a = 90.

Substituting the corresponding values into eq. (16) in order to obtain the objective function, and into eq. (17)-(20) to find the constraints, produces:

Minimize:

subject to:

The optimal solution is:

C_t = 0.47831C_c
A_s = 0.0023763 m² = 23.763 cm²
d = 0.84941 m = 84.941 cm
r = 0.00933

Fig. 2 presents the plot of the objective function and the constraint functions.

Example 1 is developed by employing the standard design method, using eq.s (4)-(10). The results are presented in Table 1. It may be seen from this table that the derived optimum design formulae for singly reinforced sections give an accurate estimate of the minimum material cost.

3.2. Case Example 2

A rectangular beam section, effective depth d = 26 cm, giving a total depth of h = 30 cm is given. Values must be determined for the optimum ratio of reinforcement steel r, its optimum area, A_s, and its optimum width b, for M_u = 700 kN-m, f'_c = 28 MPa and f_y = 420 MPa. It is assumed that r = 4 cm, and the ratio of reinforcement steel cost to concrete cost is: a = 90.

Substituting the corresponding values into eq. (21) in order to obtain the objective function and into eq.s (22)-(25) to find the constraints results in the following:

Minimize:

subject to:

The optimal solution is:

C_t = 1.25705C_c
A_s = 0.00877 m² = 87.7 cm²
b = 1.58773 m = 158.773 cm
r = 0.02125

Fig. 3 plots the objective function and the constraint functions.

Example 2 is developed by employing the standard design method, using eq. (4)-(10). The results are presented in Table 2. This table also shows the derived optimum design formulae for singly reinforced sections, giving an accurate estimate of the minimum material cost.

3.3. Case Example 3

A rectangular beam section with b = 30 cm is given. Values must be determined for the optimum ratio of reinforcement steel r, its optimum area, A_s, and the optimum effective depth, d, for M_u = 700 kN-m, f'_c = 28 MPa and f_y = 420 MPa. It is assumed that r = 4 cm, and the ratio of reinforcement steel weight to concrete weight is: g = 3.

Substituting the corresponding values into eq. (29) in order to obtain the objective function and also into eq.s (30)-(33) to find the constraints results in the following:

Minimize:

subject to:

The optimal solution is:

W_t = 0.19907W_c
A_s = 0.00381 m² = 38.1 cm²
d = 0.59814 m = 59.814 cm
r = 0.02125

Fig. 4 presents the plot of the objective function and the constraint functions.

Example 3 employs the standard design method using eq.s (4)-(10). The results are presented in Table 3. It is apparent from this table that the derived optimum design formulae for singly reinforced sections give an accurate estimate of minimum material weight.

3.4. Case Example 4

A rectangular beam section of effective depth d = 26 cm is given. Values must be determined for the optimum ratio of reinforcement steel r and its optimum width b, for M_u = 700 kN-m, f'_c = 28 MPa and f_y = 420 MPa. It is assumed that r = 4 cm, and the ratio of reinforcement steel weight to concrete weight is: g = 3.

Substituting the corresponding values into eq. (34) in order to obtain the objective function and also into eq.s (35)-(38) to find the constraints results in the following:

Minimize:

subject to:

The optimal solution is:

W_t = 0.49386W_c
A_s = 0.00877 m² = 87.7 cm²
b = 1.58773 m = 158.773 cm
r = 0.02125

Fig. 5 displays the plot of the objective function and the constraint functions.

Example 4 employs the standard design method using eq.s (4)-(10). The results are presented in Table 4. It is apparent from this table that the derived optimum design formulae for singly reinforced sections give an accurate estimate of minimum material weight.

 

4. Results

Table 1 presents the results, using the standard design method for Case Example 1. The constant parameters are: M_u, b, f'_cand f_y. The design variables are: r, A_s and d. The ranges considered vary from the minimum ratio of reinforcement steel, r_min, and the maximum ratio, r_max, allowing the variation of the effective depth, d, reinforcement steel area, A_s, and the total material cost, C_t, to be observed. The corresponding total material cost, C_t, of the beam per unit length is then obtained from eq. (39), its minimum value being 0.47842C_c $/m (in terms of the concrete cost per unit volume). Consequently, the results obtained by employing the standard design method and optimal design are equal.

Table 2 presents the results using the standard design method for Case Example 2. The constant parameters are: M_u, d, f'_cand f_y. The design variables are: r, A_s and b. The ranges considered vary between the minimum ratio of reinforcement steel, r_min, and the maximum ratio, r_max, allowing the variation of the effective depth, d, reinforcement steel area, A_s, and the total material cost, C_t, to be observed. The corresponding total material cost of the beam per unit length, Ct, is then obtained from eq. (44) and found to be 1.25705C_c $/m as its minimum value (in terms of the concrete cost per unit volume). This value corresponds to the maximum ratio of reinforcement steel r_max. Thus, the results presented by employing the standard design method and optimal design are equal.

Table 3 shows the results using the standard design method for case Example 3. The constant parameters are: M_u, b, f'_cand f_y. The design variables are: r, A_s and d. The ranges considered vary between the minimum ratio of reinforcement steel, r_min, and the maximum ratio, r_max, allowing the variation of the effective depth, d, reinforcement steel area, A_s, and the total material weight, W_t, to be observed. The corresponding total material weight W_t of the beam per unit length is then obtained from eq. (49) and found to be 0.19907W_c kN/m as its minimum value (in terms of the concrete weight per unit volume). This value corresponds to the maximum ratio of reinforcement steel r_max. Thus, the results presented by employing the standard design method and optimal design are equal.

Table 4 presents the results using the standard design method for case Example 4. The constant parameters are: M_u, d, f'_cand f_y. The design variables are: r, A_s and b. The ranges considered vary between the minimum ratio of reinforcement steel, r_min, and the maximum ratio, r_max, allowing the variation of the effective depth, d, reinforcement steel area, A_s, and the total material weight W_t. The corresponding total material weight W_t of the beam per unit length is then obtained from eq. (54) and found to be 0.49386W_c kN/m as its minimum value (in terms of the concrete weight per unit volume). This value corresponds to the maximum ratio of reinforcement steel r_max. Thus, the results presented by employing the standard design method and optimal design are equal.

Therefore, the derived optimum design formulae for singly reinforced sections give a very accurate estimate of the minimum cost and minimum weight for the four Representative examples.

 

5. Conclusions

This study dealt with the design of minimum cost (Cases 1 and 2) and minimum weight (Cases 3 and 4) reinforced rectangular concrete beams for singly reinforced sections. An analytical approach to the problem, based on a criterion of minimum cost and minimum weight design, plus a set of constraints that comply with building code requirements for structural concrete (ACI 318S-13), including the comments on the standards, was formulated. Cases 1 and 3 assume that the constant parameters are: M_u, b, f'_c and f_y, and that the design variables are r, A_s and d. Cases 2 and 4 imply that the constant parameters are: M_u, d, f'_c and f_y, and that the design variables are r, A_s and b.

The standard design method (classical method) generally uses the maximum ratio of reinforcement steel to obtain the cross-section of the beam.

The research reported in this paper concludes as follows:

• Case 1: The optimum steel ratio is usually smaller than maximum ratio, r_max, and greater than minimum ratio, r_min.
• Cases 2, 3 and 4: The optimum steel ratio is equal to the maximum ratio r_max.
• According to Case 1 the optimum section is very economical compared to other sections that may be obtained using the standard design method.
• The procedure developed as a result of this research can serve as the basis for designing reinforced concrete beams, while a structure designed using the optimum section will not necessarily provide an optimum design for the entire structure in terms of material costs.

Using the optimal design for Case 1, this paper successfully developed a model to predict the reinforcement steel ratio and lowest cost of reinforced rectangular concrete beams for singly reinforced sections

Suggested future research includes: 1) Optimal design of other types of structural members for reinforced concrete and structural steel; 2) Optimum design for whole structures.

 

References

[1] Saini, B., Sehgala, V.K. and Gambhir, M.L., Genetically optimized artificial neural network based optimum design of singly and doubly reinforced concrete beams, Asian Journal of Civil Engineering (Building and Housing), [Online]. 7(6), pp. 603-619, 2006. Available at: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.133.2193&rep=rep1&type=pdf        [ Links ]

[2] Yousif, S.T., ALsaffar, I.S. and Ahmed, S.M., Optimum design of singly and doubly reinforced concrete rectangular beam sections: Artificial neural networks application, Iraqi Journal of Civil Engineering, [Online]. 6(3), pp. 1-19, 2010. Available at: http://www.iasj.net/iasj?func=fulltext&aId=14126        [ Links ]

[3] Bhalchandra, S.A. and Adsul, P.K., Cost optimization of doubly reinforced rectangular beam section, International Journal of Modern Engineering Research, [Online]. 2(5), pp. 3939-3942, 2012. Available at: http://www.ijmer.com/papers/Vol2_Issue5/FJ2539393942.pdf        [ Links ]

[4] Quimby, T.B., A Beginner's guide to the structural engineering, Quimby & Associates Consulting Engineers, [Online]. 2012. Available at: http://www.bgstructuralengineering.com/BGSCM13_Sample.pdf        [ Links ]

[5] Manual of Steel Construction LRFD (Load Resistance Factor Design), Structural Members Specifications & Codes, 3^td Edition, AISC (American Institute Steel Construction), 2009.         [ Links ]

[6] Ortiz-Pimiento, N.R. y Díaz-Serna, F.J., Validación de soluciones obtenidas para el problema del despacho hidrotérmico de mínimo costo empleando la programación lineal binaria mixta, DYNA, [Online]. 75(156), pp. 43-54, 2008. Available at: http://www.redalyc.org/articulo.oa?id=49612071005        [ Links ]

[7] Jaramillo-Alvarez, P., Gonzalez-Calderon, C.A. and Gonzalez-Calderon, G., Route optimization of urban public transportation, DYNA, [Online]. 80(180), pp. 41-49, 2013. Available at: http://www.redalyc.org/articulo.oa?id=49627455007        [ Links ]

[8] Soto-de la Vega, D., Vidal-Vieira, J.G. and Vitor-Toso, E.A., Methodology for distribution centers location through multicriteria analysis and optimization, DYNA, 81(184), pp. 28-35, 2014. DOI: 10.15446/dyna.v81n184.39654        [ Links ]

[9] Santos-Azevedo, M.S., Pérez-Abril, I., León-Benítez, C., Cabral-Leite, J. and Holanda-Bezerra, U., Multiobjective optimization of the reactive power compensation in electric distribution systems, DYNA, 81(187), pp. 175-183, 2014. DOI: 10.15446/dyna.v81n187.40979        [ Links ]

[10] Ha, T., Optimum design of unstiffened built-up girders, Journal of Structural Engineering, 119(9), pp. 2784-2792, 1993. DOI: 10.1061/(ASCE)0733-9445(1993)119:9(2784)        [ Links ]

[11] Rath, D.P., Ahlawat, A.S. and Ramaswamy, A., Shape optimization of rc flexural members, Journal of Structural Engineering, 125(2), pp. 1439-1445, 1999. DOI: 10.1061/(ASCE)0733-9445(1999)125:12(1439)        [ Links ]

[12] Ceranic, B. and Fryer, C., Sensitivity analysis and optimum design curves for the minimum cost design of singly and doubly reinforced concrete beams, Structural and Multidisciplinary Optimization, 20, pp. 260- 268, 2000. DOI: 10.1007/s001580050156        [ Links ]

[13] Jarmai, K., Snyman, J.A., Farkas, J. and Gondos, G., Optimal design of a welded I-section frame using four conceptually different optimization algorithms, Structural and Multidisciplinary Optimization, 25, pp. 54- 61, 2003. DOI: 10.1007/s00158-002-0272-5        [ Links ]

[14] Leps, M. and Sejnoha, M., New approach to optimization of reinforced concrete beams, Computer and Structures, 81, pp. 1957-1966, 2003. DOI: 10.1016/S0045-7949(03)00215-3        [ Links ]

[15] Barros, M.H.F.M., Martins, R.A.F. and Barros, A.F.M., Cost optimization of singly and doubly reinforced concrete beams with EC2-2001, Structural and Multidisciplinary Optimization, 30, pp. 236- 242, 2005. DOI: 10.1007/s00158-005-0516-2        [ Links ]

[16] Sahab, M.G., Ashour, AF. and Toropov, V.V., Cost optimization of reinforced concrete flat slab buildings, Engineering Structures, 27, pp. 313-322, 2005. DOI: 10.1016/j.engstruct.2004.10.002        [ Links ]

[17] Zou, X., Chan, C., Li, G. and Wang, Q., Multi objective optimization for performance-based design of reinforced concrete frames, Journal of Structural Engineering, 133(10), pp. 1462-1474, 2007. DOI: 10.1061/(ASCE)0733-9445(2007)133:10(1462)        [ Links ]

[18] Aschheim, M., Hernández-Montes, E. and Gil-Martin, L., Design of optimally reinforced RC beam, column, and wall sections, Journal of Structural Engineering, 134(2), pp. 231-239, 2008. DOI: 10.1061/(ASCE)0733-9445(2008)134:2(231)        [ Links ]

[19] Tang, C., Chen, H. and Yen, T., Modelling confinement efficiency of reinforced concrete columns with rectilinear transverse steel using artificial neural network, Journal of Structural Engineering, 129(6), pp. 775-783, 2003. DOI: 10.1061/(ASCE)0733-9445(2003)129:6(775)        [ Links ]

[20] Oreta, A.W.C., Simulating size effect on shear strength of RC beams without stirrups using neural networks, Engineering Structures, 26, pp. 681-691, 2004. DOI: 10.1016/j.engstruct.2004.01.009        [ Links ]

[21] Fonseca, E.T., Vellasco, P.C.G da, de Andrade, S.L. and Vellasco M.M.B.R., Neural network evaluation of steel beam patch load capacity, Advanced in Engineering Software, 34, pp. 763-772, 2003. DOI: 10.1016/S0965-9978(03)00104-2        [ Links ]

[22] Maity, D. and Saha, A., Damage assessment in structure from changes in static parameter using neural networks, Sadhana, 29, Part 3, pp. 315-327, 2004. DOI: 10.1007/BF02703781        [ Links ]

[23] Zhou, G., Deng, P., Xun, X. and Yaqub, R., Innovative ANN technique for predicting failure / cracking load of masonry wall panel under lateral load, Journal of Computing in Civil Engineering, 24(4), pp. 377-387, 2010. DOI: 10.1061/(ASCE)CP.1943-5487.0000040)        [ Links ]

[24] Al-Assaf, A. and Saffarini, H.F., Optimization of slabs using object oriented programming, Computers and Structures, 82(9-10), pp. 741-752, 2004. DOI: 10.1016/j.compstruc.2004.02.009        [ Links ]

[25] The MathWorks, Maple User Manual, The MathWorks, Inc. United States, 2010.         [ Links ]

[26] Kalashnikov, V.V., Some problems of lexicographic minimization, Optimizatsia, 21(38), pp. 109-120, 1978.         [ Links ]

[27] Kalashnikov, V.V., Separate step method for minimization of Ill-conditioned functions, Optimizatsia, 25(42), pp. 70-85, 1980.         [ Links ]

[28] Kalashnikov, V.V., Method for minimization of Ill-conditioned functions by selecting singular directions, Optimizatsia, 30(47), pp. 35-49, 1982.         [ Links ]

[29] ACI 318S-13 (American Concrete Institute), Building code requirements for structural concrete, including the comments on the standards, Committee 318, 2013.         [ Links ]

[30] González-Cuevas, O.M. y Robles-Fernández-Villegas, F., Aspectos fundamentales del concreto reforzado, Limusa, México, 2005.         [ Links ]

[31] McCormac, J.C. and Brown, R.H., Design of reinforced concrete, John Wiley & Sons, New York, 2013.         [ Links ]

 

A. Luévanos-Rojas, received a BSc. Eng. in Civil Engineering in 1981, an MSc. in Planning and Construction in 1996, and a PhD. Eng. in Planning and Construction in 2009, all from the Faculty of Engineering, Science and Architecture at the Juarez University of the State of Durango, Mexico. He was awarded an MSc. in Structures by the Higher School of Engineering and Architecture at the National Polytechnic Institute, Mexico City, in 1983 and an MSc. in Administration by the Faculty of Accounting and Administration at the Autonomous University of Coahuila, Mexico in 2004. From 1983 to 2009, he was a full time professor and -from 2009 to 2014- professor and researcher at the Faculty of Engineering, Science and Architecture at the Juarez University. His research interests include: mathematical models applied to structures, methods of structural analysis, design of concrete and steel members, and analysis of non-prismatic members. In addition, he is an Advisor and Collaborator of the "Revista de Arquitectura e Ingeniería" and Associate Editor of the journal "ICIC Express Letters Part B: Applications". He is a member of the National System of Researchers of Mexico. ORCID: 0000-0002-0198-3614.