Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
DYNA
Print version ISSN 0012-7353
Dyna rev.fac.nac.minas vol.83 no.198 Medellín Sept. 2016
https://doi.org/10.15446/dyna.v83n198.51766
DOI: http://dx.doi.org/10.15446/dyna.v83n198.51766
Modeling and behavior of the simulation of electric propagation during deep brain stimulation
Modelado y comportamiento de la simulación de propagación eléctrica durante la estimulación cerebral profunda
Pablo A. Alvarado a, Cristian A. Torres-Valencia a, Álvaro A. Orozco-Gutiérrez a, Mauricio A. Álvarez a, Genaro Daza-Santacoloma b & Hans Carmona-Villada b
a Universidad Tecnológica de Pereira, Pereira, Colombia. dapa@utp.edu.co
b Instituto de Epilepsia y Parkinson del Eje Cafetero - Neurocentro, Pereira, Colombia
Received: July 8th, 2015. Received in revised form: February 23th, 2016. Accepted: Mach 7th, 2016
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
Deep brain stimulation (DBS) is an effective treatment for Parkinson's disease. In the literature, there are a wide variety of mathematical and computational models to describe electric propagation during DBS; however unfortunately, there is no clarity about the reasons that justify the use of a specific model. In this work, we present a detailed mathematical formulation of the DBS electric propagation that supports the use of a model based on the Laplace Equation. Moreover, we performed DBS simulations for several geometrical models of the brain in order to determine whether geometry size, shape and ground location influence electric stimulation prediction by using the Finite Element Method (FEM). Theoretical and experimental analysis show, firstly, that under the correct assumptions, the Laplace equation is a suitable alternative to describe the electric propagation, and secondly, that geometrical structure, size and grounding of the head volume affect the magnitude of the electric potential, particularly for monopolar stimulation. Results show that, for monopolar stimulation, basic and more realistic models can differ more than 2900%.
Keywords: DBS; Parkinson disease; electric brain propagation; Laplace equation; FEM.
Resumen
La Estimulación Cerebral Profunda (DBS) es un tratamiento efectivo para la enfermedad de Parkinson. Gran variedad de modelos matemáticos y computacionales para describir la propagación eléctrica debido a la DBS han sido propuestos, desafortunadamente, no existe claridad sobre las razones que justifican el uso de un modelo específico. En el presente trabajo se presenta una formulación matemática detallada de la propagación eléctrica debido a DBS que soporta un modelo basado en la ecuación de Laplace. Se realizan simulaciones para diferentes modelos geométricos del cerebro para determinar si la geometría, el tamaño y la ubicación de la tierra del modelo afectan la predicción de la estimulación eléctrica mediante el uso del Método de Elementos Finitos (FEM). Los análisis teórico y experimental muestran en primera instancia que la ecuación de Laplace es adecuada para describir la propagación eléctrica en el cerebro, y en segunda instancia que la estructura geométrica, tamaño y ubicación de la tierra afectan la magnitud del potencial eléctrico, particularmente para modos de estimulación monopolar. Los resultados muestran que para modelos básicos y más realistas pueden existir diferencias en la propagación de hasta un 2900%.
Palabras Clave: Estimulación Cerebral Profunda; Ecuación de Laplace; Enfermedad de Parkinson; FEM.
1. Introduction
Parkinson's disease (PD) is a degenerative disorder of the central nervous system that results in impaired motor skills and speech. Its most prevalent symptoms are tremor and rigidity . PD is the second most common neurodegenerative disorder after Alzheimer's disease, often affecting the elderly population
. PD is the second most common neurodegenerative disorder after Alzheimer's disease, often affecting the elderly population .
.
Deep brain stimulation (DBS) is a clinically effective treatment for medically intractable PD . To improve all PD symptoms, it is best for DBS to target the Subthalamic Nucleus (STN)
. To improve all PD symptoms, it is best for DBS to target the Subthalamic Nucleus (STN)  , the brain structure related to sensorimotor, cognitive, and limbic functions
, the brain structure related to sensorimotor, cognitive, and limbic functions . The fundamental purpose of DBS is to modulate neural activity with applied electric fields
. The fundamental purpose of DBS is to modulate neural activity with applied electric fields . However, the mechanisms by which DBS works are not yet well understood
. However, the mechanisms by which DBS works are not yet well understood . In this sense, DBS´s therapeutic action seems to depend on the electrical excitation of neural elements
. In this sense, DBS´s therapeutic action seems to depend on the electrical excitation of neural elements . Moreover, there are also studies that support neuronal inhibition
. Moreover, there are also studies that support neuronal inhibition  . Other studies suggest that DBS reduces the PD symptoms through the excitation of axons and the inhibition of the dendritic activity
. Other studies suggest that DBS reduces the PD symptoms through the excitation of axons and the inhibition of the dendritic activity
To achieve successful stimulation, it is necessary to excite the intended brain areas while preventing the unintended excitation of other zones: the spread of current to non-motor areas of the STN or adjacent structures is implicated in cognitive and cognitive-motor declines [12-14]. The stimulation of the dorsolateral STN and the bottom (ventral) part of the thalamus could reduce parkinsonian tremor and trigger dyskinesias, whereas stimulation outside the STN could induce adverse effects .
.
A suitable stimulation protocol involves not only the accurate placement of the electrode inside the brain, but also the proper configuration of some electrical and geometrical parameters for the DBS device [4]. The electrical parameters for DBS are pulse width, frequency and the voltage amplitude. Additionally, each of the lead´s electrodes can be designated as anode or cathode [4], To facilitate the configuration of the DBS device it is propitious to employ computational models, this allows the electric propagation of the stimulation to be predicted as a function of the previously mentioned electrical and geometrical parameters.
These computational simulations help to visualize the electric behavior of the stimulus in the brain. In this sense, several works have developed simulators of the electric activity for DBS.
have developed simulators of the electric activity for DBS.
The mathematical and computational models found in the literature 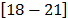 require information such as the conductivity and permittivity of brain tissue, geometrical description of the head volume, the physical laws that govern the system, and the associated equation constraints. Most of the simulation approaches are specifically based on electrostatic models. The electric potential is often computed using the Laplace
require information such as the conductivity and permittivity of brain tissue, geometrical description of the head volume, the physical laws that govern the system, and the associated equation constraints. Most of the simulation approaches are specifically based on electrostatic models. The electric potential is often computed using the Laplace  or Poisson's
or Poisson's  equation. Unfortunately, there are no major justifications about the use of this mathematical background, which is essential to define the scope, realism and accuracy of the simulation. The core of these simulations is the Finite Element Method (FEM) that has been widely used in DBS problems and other engineering fields (see [25] and [26]).
equation. Unfortunately, there are no major justifications about the use of this mathematical background, which is essential to define the scope, realism and accuracy of the simulation. The core of these simulations is the Finite Element Method (FEM) that has been widely used in DBS problems and other engineering fields (see [25] and [26]).
Previous research undertaken by authors such as [27] and [28] address some of the effects of the DBS that show some simulations from schemes different to the one proposed in this work. In [27], a latent force model was developed in order to include the dynamics of the electric propagation in the brain, unlike several state-of the-art works that only focus on the quasi-static or static approach. In [28], some propagation models following the quasi-static approach were developed using an open source library of finite element methods with no deep analysis of the physical laws that govern the DBS problem. Additionally the results are difficult to compare against the state-of the-art works due to the difference in the simulation tool used.
It is unusual to find academic discussions about the physical laws that support the behavior of the deep brain electric fields induced by an external source. In fact, there is no interpretation or explanation about the consequences of most of the mathematical simplifications carried out by the basic equations that describe the phenomenon. Moreover, in order to establish which kind of representations are appropriate to describe the electric propagation inside the human brain´s behavior, it is convenient to make a quantitative comparison of several geometrical head models, taking into account the ground positioning that is assumed by the computational algorithms.
In this work, we present a mathematical formulation of the electric propagation during DBS. Indeed, we offer an argument that sustains the use of an electrostatic propagation model based on the Laplace equation. The theoretical framework is corroborated by a set of computer simulations of the electric potential generated by DBS. Furthermore, the simulation analysis indicates that, for monopolar stimulation, the geometrical structure, size and grounding of the conducting head volume alter the magnitude of the electric field. In fact, a voltage comparison between basic and more realistic models can differ by more than 2900%.
2. Deep brain stimulation considerations
An accurate treatment of Parkinson's disease using DBS should analyze the different effects of potential propagation around the objective structure, that is the STN [15]. Adverse effects could be produced from undesired potential propagation to non-motor regions of the brain, as is presented in Fig. 1. In order to improve the Parkinsonian motor symptoms, the electrode must be placed at the motor section of the STN, as presented in Fig. 2 [15].
Given a specific electrode, e.g. the Medtronic DBS lead model 3389 that has four configurable electrodes, there are several geometrical possible arrangements to configure the stimulation parameters. In clinical practice, usually one or two stimulation contacts are used at most. Fig. 3 shows three different monopolar (Fig. 3(a)) and bipolar (Fig. 3(b)-(c)) configurations and their corresponding electric potential [8].
3. Electric stimulation modeling
Electromagnetic fields generated by DBS are dynamic since the source field or electric stimulation is time-varying and has a fundamental frequency range from 130Hz to 185Hz  (the frequency commonly used is around 140Hz). Moreover, the electric potential induced throughout the brain tissue close to the stimulating electrode is commonly modeled using the Laplace equation, which assumes a quasi-static or static field
(the frequency commonly used is around 140Hz). Moreover, the electric potential induced throughout the brain tissue close to the stimulating electrode is commonly modeled using the Laplace equation, which assumes a quasi-static or static field .
.
It is worthwhile mentioning that the quasi-static approximation is only valid when the electrodynamic system analyzed is a low frequency time-varying field . In this section, we provide a detailed explanation of how to derive the quasi-static model in order to support a DBS propagation model based on the Laplace equation. This explanation involves the use of generalized Maxwell's equations and some physical assumptions. We then present the conditions which allow us to make a decision as to whether the approximation is valid for DBS.
. In this section, we provide a detailed explanation of how to derive the quasi-static model in order to support a DBS propagation model based on the Laplace equation. This explanation involves the use of generalized Maxwell's equations and some physical assumptions. We then present the conditions which allow us to make a decision as to whether the approximation is valid for DBS.
3.1. Low frequency range, time-varying fields
The large variety of electromagnetic phenomena can all be described by a unique system of field equations known as Maxwell's equation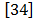 . Some particular forms of these equations have been used by other authors to model the electric propagation produced by DBS
. Some particular forms of these equations have been used by other authors to model the electric propagation produced by DBS . These equations can be simplified when slow electromagnetic fields are analyzed, i.e. fields in the so called low frequency range (up to 30kHz), when wave propagation does not play a fundamental role
. These equations can be simplified when slow electromagnetic fields are analyzed, i.e. fields in the so called low frequency range (up to 30kHz), when wave propagation does not play a fundamental role  . Before defining the situations in which wave propagation effects can be neglected, it is important to clarify some electromagnetic waves properties.
. Before defining the situations in which wave propagation effects can be neglected, it is important to clarify some electromagnetic waves properties.
Generally, electromagnetic fields propagate with a finite velocity c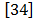 , defined as
, defined as 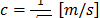 , where
, where  denotes the permittivity and
denotes the permittivity and  represents the permeability of the brain tissue
represents the permeability of the brain tissue . In addition to this,
. In addition to this, 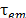 represents the time required for the electromagnetic field to propagate at a distance l from one region to another in a volume brain tissue,
represents the time required for the electromagnetic field to propagate at a distance l from one region to another in a volume brain tissue,  . The wave propagation equation for the electrodynamic scalar potential is defined as:
. The wave propagation equation for the electrodynamic scalar potential is defined as:

Where is the electric potential function, and
is the electric potential function, and  denotes the charge density
denotes the charge density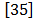 . If the field problem is considered with a characteristic spatial dimension l and a characteristic time constant
. If the field problem is considered with a characteristic spatial dimension l and a characteristic time constant , spatial and temporal differentiations can be approximated by (1/l) and (1/
, spatial and temporal differentiations can be approximated by (1/l) and (1/ ), respectively. In this case, l is related to the brain tissue volume considered, i.e. the STN and its surroundings, whereas
), respectively. In this case, l is related to the brain tissue volume considered, i.e. the STN and its surroundings, whereas 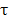 is considered as the time interval for which significant changes in the field quantities arise. For time-varying electric stimulation,
is considered as the time interval for which significant changes in the field quantities arise. For time-varying electric stimulation,  would be the reciprocal of the excitation's angular frequency,
would be the reciprocal of the excitation's angular frequency,
 . If these previous considerations are applied, equation (1) can be approximated by:
. If these previous considerations are applied, equation (1) can be approximated by:

For slow time-varying fields, the characteristic time constant  is supposed to be much greater than the transit time
is supposed to be much greater than the transit time 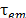 , i.e.
, i.e.  . If this expression holds, then
. If this expression holds, then  , and the propagation effects can be neglected.
, and the propagation effects can be neglected.
3.2. Static and quasi-static models
When wave propagation does not play a fundamental role, the electromagnetic field simulations of slow processes are carried out by using 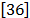 .
.
- a static model, i.e. electrostatics or magnetostatics, if all variations in time can be neglected.
- a quasi-static model, i.e. electro quasistatics or magneto quasistationary.
The static models are just special cases of the full Maxwell's equations, whereas the quasi-static models are approximations that are not always valid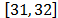 . The quasi-static models are obtained from Maxwell's equations by neglecting either the magnetic induction, or the electric displacement current, as well as the electromagnetic waves that result from their coupling
. The quasi-static models are obtained from Maxwell's equations by neglecting either the magnetic induction, or the electric displacement current, as well as the electromagnetic waves that result from their coupling .
.
The electro-quasistatic assumption establishes that the electric field E is essentially irrotational. In general, the field of gradient  (for any scalar
(for any scalar ) is purely irrotational since
) is purely irrotational since , thus the irrotational field E can always be expressed in terms of a scalar field
, thus the irrotational field E can always be expressed in terms of a scalar field , that is
, that is

The negative sign shows that the direction of E is opposite to the direction in which  increases. The electric field E looks like an electrostatic field at any tissue point. Changes in the electric stimulation will immediately take effect in the whole brain tissue volume under consideration.
increases. The electric field E looks like an electrostatic field at any tissue point. Changes in the electric stimulation will immediately take effect in the whole brain tissue volume under consideration.
3.2. Magneto-quasistationary model
Analogously, the magneto-quasistationary models are characterized by setting the magnetic field H as solenoidal. This implies that the divergence of current density J is zero, i.e.

3.2.3. Laplace equation
If electro-quasistatic and magneto-quasistationary approximations are simultaneously applied, then all temporal variations in Maxwell's equations are neglected. This does not mean, however, that the sources, and hence the fields, are not functions of time. But, given the sources at a certain instant, the fields at that same instant are determined without regard for what the sources of fields were an instant earlier. Using Maxwell's equations and Ohm's law, the Laplace equation used to model the electric potential in DBS can be derived. The current density J is related to the electric field E by Ohm's law as follows 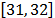 :
:

Where 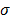 is the tissue conductivity. It is measured in Siemens per meter (S/m). If the divergence is applied on both sides of (3), we have
is the tissue conductivity. It is measured in Siemens per meter (S/m). If the divergence is applied on both sides of (3), we have , and using (2) we get the Laplace equation:
, and using (2) we get the Laplace equation:

Equation (4) corresponds to an inhomogeneous tissue. For a homogeneous tissue, equation (4) becomes:

In order to obtain Equation (5), the conductivity 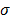 is assumed constant throughout the tissue region in which
is assumed constant throughout the tissue region in which  is defined. The Laplacian operator
is defined. The Laplacian operator 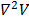 can be defined in Cartesian coordinates in the following way:
can be defined in Cartesian coordinates in the following way:

The electric potential calculation is based on a model with a homogeneous tissue medium to reduce model complexity. Several authors have developed their experiments using this assumption . Furthermore, the STN is cytologically homogeneous, i.e., neurons are identical in every part of the nucleus
. Furthermore, the STN is cytologically homogeneous, i.e., neurons are identical in every part of the nucleus . We will now present four examples of the electric field (E) propagation obtained solving the Laplace equation (5) for a finite, homogeneous, and isotropic volume tissue, using different geometries and boundary conditions. The red arrows in Fig. 4 correspond to the electric field. Fig.4 (a) and 4(b) show a cubic geometry, in Fig. 4(a) just one side of the cube is grounded, in Fig. 4(b) all sides of the cube are grounded. Likewise, Fig. 4(c) and 4(d) show the electric field distribution (see Equation (2)) obtained for a spherical geometry. In Fig. 4(c) a small base is grounded, whereas in Fig. 4(d) all the external surface of the sphere is grounded.
. We will now present four examples of the electric field (E) propagation obtained solving the Laplace equation (5) for a finite, homogeneous, and isotropic volume tissue, using different geometries and boundary conditions. The red arrows in Fig. 4 correspond to the electric field. Fig.4 (a) and 4(b) show a cubic geometry, in Fig. 4(a) just one side of the cube is grounded, in Fig. 4(b) all sides of the cube are grounded. Likewise, Fig. 4(c) and 4(d) show the electric field distribution (see Equation (2)) obtained for a spherical geometry. In Fig. 4(c) a small base is grounded, whereas in Fig. 4(d) all the external surface of the sphere is grounded.
3.3. Conditions for the quasistatic approximation
The validity of an approximation for a given slow time-varying field problem is determined by an analysis based on significant time constants . In this sense, two constants are defined, the time constant of dielectric relaxation
. In this sense, two constants are defined, the time constant of dielectric relaxation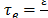 , and the constant of magnetic diffusion
, and the constant of magnetic diffusion . In addition, the transit time
. In addition, the transit time  is the geometric average of
is the geometric average of  and
and 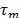 .
.

The electro-quasistatic and magneto-quasistationary approximations can be used if the relative error of the electric field and magnetic field calculated under these approximations are much smaller than one. In order to estimate this error, time derivatives in Maxwell's equations are substituted by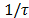 . Furthermore, only the scalar magnitudes of the fields are considered. All properties of the brain tissue are assumed to be homogeneous, linear and isotropic. The relative error
. Furthermore, only the scalar magnitudes of the fields are considered. All properties of the brain tissue are assumed to be homogeneous, linear and isotropic. The relative error  of the electric field within the electro-quasistatic approximation is defined as:
of the electric field within the electro-quasistatic approximation is defined as:

If this condition holds, electric fields can be calculated accurately by using the electro-quasistatic approximation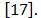 Likewise, the relative error
Likewise, the relative error  of the magnetic field within the magneto-quasistationary approximation is
of the magnetic field within the magneto-quasistationary approximation is

Magnetic fields can be calculated by using the magneto-quasistationary approximation if this condition holds.
4. Experimental background
To be allowed to use the electro-quasistatic and magneto-quasistationary approximations to model the electric potential produced by DBS, the approximation errors (6) and
(6) and  (7) have to be much less than one. To verify this, the approximation errors were calculated for different l radius and stimulation frequencies. The dielectric properties of the tissue are frequency dependent
(7) have to be much less than one. To verify this, the approximation errors were calculated for different l radius and stimulation frequencies. The dielectric properties of the tissue are frequency dependent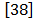 , and the electric field propagation time
, and the electric field propagation time  is a function of the spatial quantity l
is a function of the spatial quantity l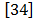 . Therefore, the errors
. Therefore, the errors  (6) and
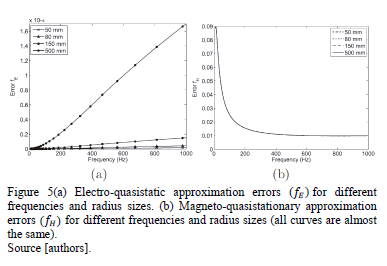
(6) and  (7) depend on the stimulation frequency and the size of the brain tissue region considered. The errors obtained for different frequencies (100Hz up to 1 kHz), assuming a radius of l = 50mm, l = 80mm, l = 150mm and l = 500mm, are shown in Fig. 5. According to the Andreuccetti online dataset
(7) depend on the stimulation frequency and the size of the brain tissue region considered. The errors obtained for different frequencies (100Hz up to 1 kHz), assuming a radius of l = 50mm, l = 80mm, l = 150mm and l = 500mm, are shown in Fig. 5. According to the Andreuccetti online dataset , white matter dielectric property values where considered.. Based on Fig. 5, and assuming that all properties of the brain tissue arehomogeneous, linear and isotropic, we can conclude that the electro-quasistatic and magneto-quasistationary approximations are valid for a radius of between l = 50mm and l = 500mm, and a frequency band from 100Hz to 1kHz.
, white matter dielectric property values where considered.. Based on Fig. 5, and assuming that all properties of the brain tissue arehomogeneous, linear and isotropic, we can conclude that the electro-quasistatic and magneto-quasistationary approximations are valid for a radius of between l = 50mm and l = 500mm, and a frequency band from 100Hz to 1kHz.
Works such as  and
and  use several sizes of geometrical models in 2D and 3D. These include specifications of the DBS lead shape that go into a monopolar configuration and the specification for the tissue conductivity properties of the region analyzed. Usually, two different ground configurations of the electrical models are used, one to define all the boundaries of the geometrical model, such as the ground, and the other to configure a specific area of the model, such as the ground
use several sizes of geometrical models in 2D and 3D. These include specifications of the DBS lead shape that go into a monopolar configuration and the specification for the tissue conductivity properties of the region analyzed. Usually, two different ground configurations of the electrical models are used, one to define all the boundaries of the geometrical model, such as the ground, and the other to configure a specific area of the model, such as the ground  In
In , one model is developed assuming an infinite homogeneous and isotropic medium to compute the electric propagation in different large frequencies. In
, one model is developed assuming an infinite homogeneous and isotropic medium to compute the electric propagation in different large frequencies. In  , a detailed model of the tissue surrounding the DBS lead is built using information from magnetic resonance imaging (MRI). The model is used to assess the influence of the tissue information when the electric field surrounding the electrode is computed. It should be noted that, for future work, the patient real head shape could be included and studied in order to increase the model´s realism. Research such as [42] where a reconstruction of the head from MRI is performed could be useful.
, a detailed model of the tissue surrounding the DBS lead is built using information from magnetic resonance imaging (MRI). The model is used to assess the influence of the tissue information when the electric field surrounding the electrode is computed. It should be noted that, for future work, the patient real head shape could be included and studied in order to increase the model´s realism. Research such as [42] where a reconstruction of the head from MRI is performed could be useful.
5. Results
The propagation of the electric potential in the simulated models is obtained by solving the Laplace equation from the finite element method (FEM) using Comsol Multiphysics (COMSOL Inc., Burlington, MA). As the theoretical analysis in section 2 demonstrated how the electric potential propagation is conductivity independent when a homogeneous medium is considered, the results obtained from these models allows for the geometry to be analyzed and for building effects to be modeled in the Laplace equation solution.. The main objective of this work is to present a detailed analysis of the electrostatic process that governs the electric propagation during DBS. Several DBS simulations based on the development of geometrical models of the brain that confirm the theoretical analysis of the electric propagation were built. The presented models include more realistic geometries that allow better analysis of the stimulation results. Different ground configurations and boundary constraints are proposed to determine the influence of the ground in terms of the electric propagation results. The electrical conductivity of a homogeneous medium is not taken into account because it has no influence over the solution obtained through the Laplace equation.
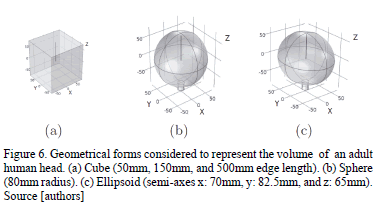
Three geometrical forms are considered to represent the volume of an adult human head. The first form is a cubic model (Fig. 6(a)), where the edge length is fixed to 50mm, 150mm, and 500mm, in order to study the changes in the electric propagation when the head volume is small, normal, and large. The second geometry corresponds to a spherical model with a radius 80mm (see Fig. 6(b)). Finally, as in , we created an ellipsoidal model with semi-axes measuring 70mm, 82.5mm and 65mm in the x, y, and z directions respectively (Fig. 6(c)). The last two geometrical forms and sizes are more realistic representations of the head, facilitating the interpretation of simulated electric potential propagation during DBS. Moreover, a Medtronic 3389 DBS lead in monopolar configuration with a stimulus voltage of -1V was used; other material properties were discarded in the idealized FEM representation by using the Laplace equation in a homogeneous medium.
, we created an ellipsoidal model with semi-axes measuring 70mm, 82.5mm and 65mm in the x, y, and z directions respectively (Fig. 6(c)). The last two geometrical forms and sizes are more realistic representations of the head, facilitating the interpretation of simulated electric potential propagation during DBS. Moreover, a Medtronic 3389 DBS lead in monopolar configuration with a stimulus voltage of -1V was used; other material properties were discarded in the idealized FEM representation by using the Laplace equation in a homogeneous medium.
All the cubic models were analyzed with two different ground configurations following the Dirichlet boundary conditions; one uses the base of the cube as ground and the second uses all the sides of the cube as ground. For the spherical and ellipsoidal models, two ground configurations were used. The first configuration has all the surface settled at  . For the second configuration, a cylinder (28 mm in diameter and 20mm in height) on the base of the model was included. The cylinder represents the path that the return current should follow to the reference electrode placed in the chest cavity, then the base of the cylinder is considered as ground. The models use an adaptive mesh refinement for the FEM in order to improve the precision of particular small regions of the model: the region closer to the electrode.
. For the second configuration, a cylinder (28 mm in diameter and 20mm in height) on the base of the model was included. The cylinder represents the path that the return current should follow to the reference electrode placed in the chest cavity, then the base of the cylinder is considered as ground. The models use an adaptive mesh refinement for the FEM in order to improve the precision of particular small regions of the model: the region closer to the electrode.
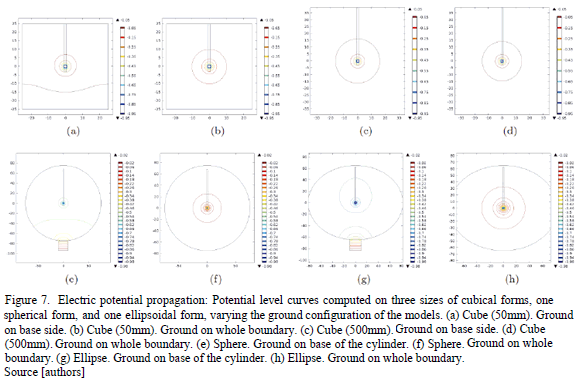
Results obtained from the solution of the Laplace equation using FEM are presented as curves around the active contact of the electrode. These represent ten different levels of potential as the distance from the electrode increases in the y-z plane (coronal view). These potential curves are obtained for all the models following the above mentioned ground configurations. Fig.7 (a) and 7(b) show the results for the 50mm edge length cube. A large difference in the potential levels between ground configuration models as function of the distance is observed. When the base side of the cube is set to , higher electric potential levels can be found at larger distances from the electrode in comparison with the case in which all the sides of the cube are set to
, higher electric potential levels can be found at larger distances from the electrode in comparison with the case in which all the sides of the cube are set to . Also, the shape of the potential curves is influenced by the position of the ground. It becomes a uniform circle when all the boundaries are used. The same calculations are undertaken for the 150mm and 500mm edge length cubes. Similar behavior to the electric potential levels is shown in Fig.7(c) and 7(d), which compares to the results for the 50mm edge length cube.
. Also, the shape of the potential curves is influenced by the position of the ground. It becomes a uniform circle when all the boundaries are used. The same calculations are undertaken for the 150mm and 500mm edge length cubes. Similar behavior to the electric potential levels is shown in Fig.7(c) and 7(d), which compares to the results for the 50mm edge length cube.
Moreover, when the size of the cube increases, the influence of the ground configuration becomes less determinant in the shape and level of the potential. Fig. 7(f) and 7(e) show the results of ten potential curves for the two different ground configurations of the spherical models. The same results are presented in Fig. 7(h) and 7(g) for the ellipsoidal model. The influence of the ground when the cylinder configuration is used can be noticed, and it has higher potential levels in farther regions from the electrode.
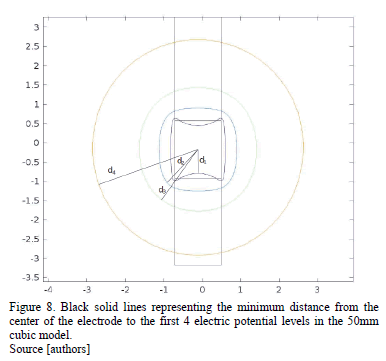
In order to better understand the results, a quantitative assessment was developed to measure the electric potential in the regions that surround the electrode in order to determine the change in the electric propagation pattern according to different geometries. According to the solution of the models, the distances from the center of the electrode to each point of a single potential curve were computed. In order to measure the distance of different potential levels in the analyzed region, the Euclidean distance from the electrode to every point within a potential curve is calculated using
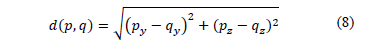
where q is the origin and p is one point placed on a potential level curve from the coronal view; 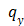 ,
, 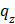 ,
,  , and
, and  are the components on the
are the components on the 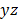 plane. This Euclidean distance is calculated for every model, and 100 different potential levels of propagation are analyzed. After the distance from the center of the electrode to each point of the equipotential curve has been computed, the minimum distance for each potential curve is selected (Fig. 8 describes the methodology), using:
plane. This Euclidean distance is calculated for every model, and 100 different potential levels of propagation are analyzed. After the distance from the center of the electrode to each point of the equipotential curve has been computed, the minimum distance for each potential curve is selected (Fig. 8 describes the methodology), using:
Fig. 9(d) shows the results from the spherical and ellipsoidal forms. In the cylinder-base grounded models, the electric potential reaches higher values at distances far from the electrode until an inflexion point is reached. After the inflection point, the potential starts to decrease linearly alongside the cylinder region. The analysis of the electric potential before the inflection point shows that it is represented by a monotonically increasing function that behaves similarly to the potential for the models without the cylinder ground configuration.
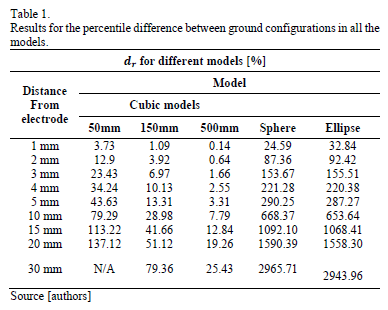
Furthermore, Table 1 presents the information regarding the percentile difference of electric potential between each model's two boundary conditions at specific distances (1, 2, 3, 4, 5, 10, 15, 20, and 30mm) from the center of the electrode. This is computed as in Equation (10):

where 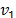 and
and 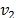 represent the value of the potential at a specific distance of the two different ground configurations of the same model,
represent the value of the potential at a specific distance of the two different ground configurations of the same model, 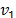 for the model with all the boundaries and
for the model with all the boundaries and 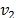 for the model with the ground placed on the base side.
for the model with the ground placed on the base side.
The value of the electric potential at the fixed distances from the electrode is obtained from linear interpolation of the curves from the minimum distances. The size of the model influences the propagation of the electric potential; lower levels of potential are reached for the smaller models in comparison with the larger models as the distance from the electrode increases. This result confirms that building a realistic model of DBS should consider size and boundary conditions due to the direct influence of these parameters on the final solution of the electric potential propagation.
6. Discussion
The results obtained in this work could be compared to studies such as [17, 18] and [19] in which simulation models were built for the same DBS electrode; however, there were a lack of real metrics that allowed a better understanding of the simulation results such as the ones presented in this work. Additionally, simulations for different ground configurations were not presented in the previously mentioned state-of-the-art studies, but they were in this present work.
Based on results, the size of the model and the ground configuration are important parameters when modeling a specific DBS simulation. The boundary conditions specified for the ground configuration and the size of the different models directly affect the shape and the magnitude of the electric potential in the region surrounding the electrode. This can be seen in all the results for the different models in Fig. 7. For the smaller models, the pattern of propagation of the potential is more influenced by the ground, more negative potential levels are reached far from the electrode, in comparison to bigger sized models. The shape of the potential levels around the electrode also changes for the two different ground configurations. When all the model's surfaces are grounded (Figs. 7(b), 7(d), 7(e) and 7(h)), a uniform potential distribution can be observed around the electrode, and a non-uniform shape of the potential levels can be found when the base side of the models is grounded (Figs. 7(a), 7(c), 7(f) and 7(g)).
For the quantification analysis presented in Fig. 9, it can be noticed that for the models with the ground configured in the whole surface, the higher potential levels reach shorter distances from the electrode than they do for the models in which only the base side is settled to  .
.

From Table 1 it is possible to determine that for the cubic models the larger the size of the cube the less the influence of the ground configuration. In the case of the spherical and ellipsoidal models, since the results of the potential level propagation changes considerably when the base of the cylinder corresponds to the ground, the percentile difference between the two configurations for these models is larger than for the cubic models. Differences are reached of up to 2900% between the two different ground configurations for some distances from the electrode. Even the comparative result shows a clear difference between the ground configurations applied to the models. The development of a DBS realistic model should include tissue, electrical properties and other boundary conditions. From all of these assumptions, a DBS model could give more realistic results. From the DBS modeling presented, several applications could be derived; for example, a work presented by Michmizos et al. in [43] details the process of predicting the Parkinsonian STN spikes using the local field potentials that could be obtained using this approach.
7. Conclusion
We have described the electromagnetic phenomena that take place during DBS using classical electromagnetic theory. Moreover, we have shown that under the correct assumptions, the Laplace equation is a suitable alternative to represent the electrostatic field propagation generated after the stimulation. We have also shown through different computer simulations how factors such as the geometrical structure, size and the grounding of the conducting head volume have dramatic effects over the magnitude of the electric field, particularly for monopolar stimulation.
Acknowledgments
Author P.A.A was funded by the program 617 "Jóvenes Investigadores e Innovadores" funded by Colciencias. Author C.A.T. thanks the program "Formación de alto nivel para la ciencia, la tecnología la innovación - Doctorado Nacional - Convoctoria 647 de 2014" and the research project 111045426008 funded by Colciencias and UTP. Author GDS was partially supported by "Patrimonio Autónomo Fondo Nacional de Financiamiento para la Ciencia, la Tecnología y la Innovación, Francisco José de Caldas", by project number 499153-530997. This work was also supported by the projects 111045426008 and 111056934461, both funded by Colciencias.
References
[1] Benabid, A.L., Chabardes, S., Mitrofanis, J. and Pollak, P., Deep brain stimulation of the subthalamic nucleus for the treatment of Parkinson's disease. The Lancet Neurology, 8(1), pp.67-81, 2009. [ Links ]
[2] de Lau, L.M. and Breteler, M.M., Epidemiology of parkinson's disease. The Lancet Neurology, 5(6), pp. 525-535, 2006. DOI: 10.1016/S1474-4422 (06)70471-9. [ Links ]
[3] Limousin, P., Pollak, P., Benazzouz, A., Hoffmann, D., Bas, J.F.L., Perret, J., Benabid, A.L. and Broussolle, E., Effect on parkinsonian signs and symptoms of bilateral subthalamic nucleus stimulation. The Lancet Neurology, 345(8942), pp. 91-95, 1995. DOI: 10.1016/S0140-6736 (95)90062-4. [ Links ]
[4] Benabid, A.L., Deep brain stimulation for parkinson's disease. Current Opinion in Neurobiology, 13(6), pp. 696-706, 2003. DOI: 10.1016/j.conb.2003.11.001, URL http://www.sciencedirect.com/science/article/pii/S0959438803001739. [ Links ]
[5] Visser-Vandewalle, Y.T., The functional role of the subthalamic nucleus in cognitive and limbic circuits. Progress in Neurobiology, 76, 2005. DOI: 10.1016/j.pneurobio.2005.09.005. [ Links ]
[6] Chaturvedi, A., Butson, C.R., Lempka, S.F., Cooper, S.E. and McIntyre, C.C., Patient-specific models of deep brain stimulation: Influence of field model complexity on neural activation predictions. Brain Stimulation, 3, pp. 65-77, 2010. [ Links ]
[7] Kuncel, A.M. and Grill, W.M., Selection of stimulus parameters for deep brain stimulation. Clinical Neurophysiology, 115, pp. 2431-2441, 2004. [ Links ]
[8] Montgomery, E.B., Deep brain stimulation programming. Principles and practice. Oxford University Press, USA, 2010. [ Links ]
[9] Obeso, J.A., Marin, C., Rodriguez-Oroz, C., Blesa, J., Benitez, B., Mena-Segovia, J., Rodríguez, M. and Olanow, C.W., The basal ganglia in Parkinson's disease: Current concepts and unexplained observations, Annals of Neurology, 64(S2), pp. S30-S46, 2008. DOI 10.1002/ana.2148. [ Links ]
[10] Obeso, J.A., Rodríguez-Oroz, M.C., Benitez-Temino, B., Blesa, F.J., Guridi, J., Marin, C. and Rodriguez, M., Functional organization of the basal ganglia: Therapeutic implications for parkinson's disease, Movement Disorders, 23(S3), pp. S548- S559, 2008. DOI 10.1002/mds.22062, [ Links ]
[11] Vitek, J.L., Mechanisms of deep brain stimulation: Excitation or inhibition, Movement Disorders, 17(S3), pp. S69-S72, 2002. DOI 10.1002/mds.10144. [ Links ]
[12] Volkmann, J., Herzog, J., Kopper, F. and Deuschl, G., Introduction to the programming of deep brain stimulators. Movement Disorders, 17(S3), pp. S181-S187, 2002. DOI: 10. 1002/mds.10162. [ Links ]
[13] Krack, P., Fraix, V., Mendes, A., Benabid, A.L. and Pollak, P., Postoperative management of subthalamic nucleus stimulation for parkinson's disease. Movement Disorders, 17(S3), pp. S188-S197, 2002. DOI: 10.1002/mds.10163, [ Links ]
[14] McIntyre, C.C., Frankenmolle, A.M., Wu, J., Noecker, A.M. and Alberts, J.L., Customizing deep brain stimulation to the patient using computational models. In: 31st Annual International Conference of the IEEE EMBS, Mineapolis, MN, USA, pp 4228-4229, 2009. [ Links ]
[15] Pollak, P., Krack, P., Fraix, V., Mendes, A., Moro, E., Chabardes, S. and Benabid, A.L., Intraoperative micro- and macroestimulation of the subthalamic nucleus in Parkinson's disease. Movement Disorders, 17(3), pp. S155-S16, 2002. [ Links ]
[16] McIntyre, C.C., Butson, C.R., Maks, C.B. and Noecker, A., Optimizing deep brain stimulation parameter selection with detailed models of the electrode-tissue interface. In: 28th Annual International Conference of the IEEE EMBS, New York, NY, USA, pp 893-895, 2006. [ Links ]
[17] Grant, P.F. and Lowery, M.M., Electric field distribution in a finite-volume head model of deep brain stimulation. Medical Engineering & Physics, 31, pp. 1095-1103, 2009. [ Links ]
[18] Schmidt, C. and van Rienen, U., Modeling the field distribution in deep brain stimulation: The influence of anisotropy of brain tissue. IEEE Transactions on Biomedical Engineering, 59(6), pp. 1583-1592, 2012. [ Links ]
[19] McIntyre, C.C., Morib, S., Shermanc, D.L., Thakorc, N.V. and Vitek, J.L., Electric field and stimulating influence generated by deep brain stimulation of the subthalamic nucleus. Clinical Neurophysiology, 115, pp. 589-595, 2004. [ Links ]
[20] Walckiers, G., Fuchs, B., Thiran, J.P., Mosig, J.R. and Pollo, C., Influence of the implanted pulse generator as reference electrode in finite element model of monopolar deep brain stimulation. Journal of Neuroscience Methods, 186, pp. 90-96, 2010. [ Links ]
[21] Liberti, M., Apollonio, F., Paffi, A., Parazzini, M., Maggio, F., Novellino, T., Ravazzani, P. and D'Inzeo, G., Fundamental electrical quantities in deep brain stimulation: Influence of domain dimensions and boundary conditions. In: 29th Annual International Conference of the IEEE EMBS, Lyon, France, pp 6668-6671, 2007. [ Links ]
[22] McIntyre, C.C. and Grill, W.M., Extracellular stimulation of central neurons: Influence of stimulus waveform and frequency on neuronal output. Journal of Neurophysiology, 88, pp. 1592-1604, 2002. [ Links ]
[23] Martens, H., Toader, E., Decr, M., Anderson, D., Vetter, R., Kipke, D., Baker, K.B., Johnson, M.D. and Vitek, J.L., Quasi-stationary fields for microelectronic applications. Clinical Neurophysiology, 122, pp. 558-566, 2011. [ Links ]
[24] Butson, C.R. and McIntyre, C.C., Tissue and electrode capacitance reduce neural activation volumes during deep brain stimulation. Clinical Neurophysiology, 116, pp. 2490-2500, 2005. [ Links ]
[25] Alvarez-Alvarez, D., Rosero-Garcia, J. and Mombello, E., Core influence on the frequency response analysis (FRA) of power transformers through the finite element method. Ingeniería e Investigación, 35(1Sup), pp. 110-117. 2015. DOI: 10.15446/ing.investig.v35n1Sup.53771. [ Links ]
[26] Linero-Segrera, D., Oliver, J. and Huespe, A., Numerical modelling of the fracture process in reinforced concrete by means of a continuum strong discontinuity approach. Part II: application to shear panels. Ingeniería e Investigación, 30(3), pp. 16-26, 2010. [ Links ]
[27] Alvarado, P.A., Alvarez, M.A., Daza-Santacoloma, G., Orozco, A. and Castellanos-Dominguez, G., A latent force model for describing electric propagation in deep brain stimulation: A simulation study. In: Engineering in Medicine and Biology Society (EMBC), 2014 36th Annual International Conference of the IEEE, pp. 2617-2620, 2014. [ Links ]
[28] Torres-Valencia, C.A., Daza-Santacoloma, G., Álvarez-López, M.A. and Orozco-Gutiérrez, Á.Á., Deep brain stimulation modeling for several anatomical and electrical considerations. Iteckne, 11(2), pp. 140-148. 2014. [ Links ]
[29] Volkmann, J., Herzog, J., Kopper, F. and Deuschl, G., Introduction to the programming of deep brain stimulators. Mov Disord, 17, pp. S181-S187, 2002. [ Links ]
[30] O'Suilleabhain, P., Frawley, W., Giller, C. and Dewey, R., Tremor response to polarity, voltage, pulsewidth and frequency of thalamic stimulation. Neurology, 60, pp. 786-790, 2003. [ Links ]
[31] Steinmetz, T., Kurz, S. and Clemens, M., Domains of validity of quasistatic and quasistationary field approximations. In: 15th International Symposium on Theoretical Electrical Engineering ISTET, Lubeck, Germnay, pp 271-275, 2009. [ Links ]
[32] Schmidt, K., Sterz, O. and Hiptmair, R., Estimating the eddy-current modelling error. IEEE Trans Magn, 44(6), pp. 686-689, 2008. [ Links ]
[33] Saville, D.A., Electrohydrodynamics: The taylor melcher leaky dielectric model. Annual Rev Fluid Mech, 29, pp. 27-64, 1997. [ Links ]
[34] Dirks, H.K., Quasi-stationary fields for microelectronic applications. Electrical Engineering, 79, pp. 145-155, 1997. [ Links ]
[35] Sadiku, M.N.O., Elements of electromagnetics. Oxford University Press, USA, 2002. [ Links ]
[36] Ostrowski, J., Hiptmair, R., Kramer, F., Smajic, J. and Steinmetz, T., Transient full Maxwell computation of slow processes. In: 8th Scientific Computation in Electrical Engineering conference SCEE, Toulouse, France, pp 87-95, 2010. [ Links ]
[37] Carpenter, M., Anatomy of the corpus striatum and brain stem integrating systems. John Wiley & Sons, Inc., 1981. [ Links ]
[38] Bossetti, C.A., Birdno, M.J. and Grill, W.M., Analysis of the quasi-static approximation for calculating potentials generated by neural stimulation. Journal of Neural Engineering, 59(5), pp. 44-53, 2008. [ Links ]
[39] Andreuccetti, D., Fossi, R. and Petrucci, C., An internet resource for the calculation of the dielectric properties of body tissues in the frequency range 10 hz - 100 ghz. IFAC-CNR, Florence, Italy, 1997, pp 87-95. [ Links ]
[40] Hofmanis, J., Louis-Dorr, V., Cecchin, T., Caspary, O. and Koessler, L., Propagation of electrical field in the brain using electrical intra-cerebral stimulations. In: Engineering in Medicine and Biology Society, EMBC, 2011 Annual International Conference of the IEEE, pp 3888-3891, 2011. DOI 10.1109/IEMBS.2011.6090966. [ Links ]
[41] Iacono, M.I., Makris, N., Mainardi, L.T., Angelone, L.M. and Bonmassar, G., Mri-based multiscale model for electromagnetic analysis in the human head with implanted dbs. Comp Math Methods in Medicine [Online]. 2013. Available at: http://dblp.uni-trier.de/db/journals/cmmm/cmmm2013.html#IaconoMMAB13 [ Links ]
[42] Forero, M. and Zulanga, D., Medical station for image processing and visualization of the brain electrical activity on a three-dimensional reconstruction of the patient's head. Ingeniería e Investigación, 23(3), pp. 31-38, 2010. [ Links ]
[43] Michmizos, K., Sakas, D. and Nikita, K., Prediction of the timing and the rhythm of the parkinsonian subthalamic nucleus neural spikes using the local field potentials. Information Technology in Biomedicine, IEEE Transactions on, 16(2), pp. 190-197, 2012. DOI 10.1109/TITB.2011.2158549. [ Links ]
P.A. Alvarado, is interested in probabilistic approaches for modeling music signals, with a focus on Gaussian processes and kernel methods. Alvarado holds an Electronic Engineering degree from Universidad Tecnológica de Pereira, Colombia, and a MSc in Electric Engineering from the UTP. Alvarado is currently a member of Centre for Digital Music pursuing a PhD at Queen Mary University of London. ORCID: 0000-0002-9347-5093
C.A. Torres-Valencia, received his BSc. in Electronic Engineering in 2010 from the Universidad del Quindío, his MSc. in Electric Engineering in 2013 from the Universidad Tecnológica de Pereira, Colombia. From 2011 to date, he has been working in the Automatics research group at the Universidad Tecnológica de Pereira. Currently he is a Doctoral student at the Universidad Tecnológica de Pereira and funded by Colciencias´ "Doctorado Nacional - 647" program. His research interests include image processing, biosignal processing, neuroengineering and machine learning. ORCID: 0000-0001-7568-6148
A.A. Orozco-Gutierrez, received a degree Electric Engineering in 1985, a MSc. degree in Electric Engineering in 2004, both from the Universidad Tecnológica de Pereira, and a PhD in Bioengineering from the Universidad Politécnica de Valencia in 2009. He is currently an Associate Professor at the Universidad Tecnológica de Pereira. His research interests include instrumentation and control, bioengineering and biosignal processing. ORCID: 0000-0002-1167-1446
M.A. Álvarez López, received a degree BSc. in Electronic Engineering from the Universidad Nacional de Colombia in 2004, a MSc. degree in Electrical Engineering from the Universidad Tecnológica de Pereira, Colombia, and a PhD in Computer Science from the University of Manchester, UK, in 2011. He is currently an associate professor at the Universidad Tecnológica de Pereira, Colombia. His research interests include probabilistic models, kernel methods and stochastic processes. ORCID: 0000-0002-8980-4472
G. Daza-Santacoloma received a BSc. in Electronic Engineering in 2005, a MSc. in Engineering Industrial Automation with honors in 2007, and a PhD. in Engineering - Automatics with honors in 2010, from the Universidad Nacional de Colombia. Currently, he is the R&D Manager at Neurocentro (Pereira - Colombia) where he is researching Neuroengineering. His research interests include neuroscience, feature extraction/selection for training pattern recognition systems, artificial vision, and machine learning. ORCID: 0000-0002-1429-5925
H. Carmona-Villada, received a Medical degree in 1995 from the Universidad Tecnologica de Pereria, an MSc in Neurosurgery in 1999 from the Universidad Catolica de Chile, and a Subspecialist degree in functional neurosurgery in 2002, from the Albert Ludwig University from Freiburg, Germany. Currently, he is the Scientific Manager at Neurocentro (Pereira - Colombia) and the head of the functional neurosurgery program in Neurocentro and Colombia´s Neurological Institute where he undertakes movement disorder surgery, epilepsy surgery and pain surgery. His research interests include neuromodulation, neuroengineering, brain mapping, intraoperative monitoring. ORCID: 0000-0002-8099-9461