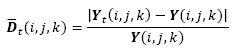English (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
1. Introduction
Remote sensors allow the atmosphere, the terrestrial surface, and the oceans to be characterized for Earth observation. The number of remote sensing applications has increased over the years, and this has encouraged the development of diverse systems and sensors. One example of remote sensing systems is the passive sensors that collect both spatial and spectral information. Multispectral and hyperspectral sensors measure the emitted and reflected radiance of a surface along the electromagnetic spectrum [1]. Multispectral sensors have a relatively small number of non-contiguous bands (i.e. less than 25 bands). Furthermore, hyperspectral sensors capture spectral information along hundreds of narrow bands. Spatial and spectral information from hyperspectral and multispectral sensors can be seen as a cube, in which each pixel is a spectral signature that characterizes the components on the surface [1].
The increasing availability of high and medium resolution remote sensors has opened new possibilities for Earth exploration, and, at the same time, image processing researchers face new challenges. One such challenge is the analysis and processing of remote sensing imagery that integrates both spatial and spectral information [2-3]. It is expected that spatial-spectral approaches improve the classification results and the estimation of sub-pixel information. Image classification identifies the classes in a dataset and assigns label to each pixel [1]. The integration of spatial information in the analysis of remote sensing data can be performed in several ways. For instance, Jimenez et al. [4] used the information within the neighborhood of a pixel to refine the classification results. The most frequent class in the neighborhood determines the final label of a pixel. Another way to include spatial information is by using segmentation techniques [5-7]. Segmentation divides the image into spectrally uniform regions, but it requires either a similarity threshold or a priori knowledge about the number of regions.
This paper explores multiscale representation to improve hyperspectral imagery classification. A multiscale representation builds a family of images, systematically removes fine details [8]. Unlike segmentation and kernel techniques, multiscale representation provides a way to explore the objects and regions within hyperspectral images in a natural and automatic way [9-11]. Different approaches are used to build a multiscale representation. For instance, nonlinear diffusion [10,11] obtains a multiscale representation by successively filtering. On other hand, binary partition tree [12-14] builds a multiscale representation by region growing. This paper aims to determine which of these approaches provides the best representation of hyperspectral imagery for classification purposes. Both representation approaches generate a family of images; thus, a scale selection criteria needs to be used. This study shows that both multiscale representations improve the classification of hyperspectral imagery, and one selection criterion is recommended in order to determine the suitable scale for the classification analysis.
The next section describes both the nonlinear diffusion and binary partition tree representations. Four scale selection criteria are subsequently presented. Section 4 shows the experiments that use a real hyperspectral image. The final section contains the conclusions and future work.
2. Multiscale Representation
Two multiscale representation approaches are explored for the classification of hyperspectral imagery. First, nonlinear diffusion is presented, and then binary partition tree is presented. Both approaches seek to deal with the scale notion, however, the first address the problem from a filtering perspective and the second from a region growing perspective.
2.1. Nonlinear diffusion
A multiscale representation of a hyperspectral image 
with n spectral bands and m pixels is obtained by systematically solving the partial differential equation -PDE, given by:
(1)
where y σ is the result of a Gaussian filter with zero mean and standard deviation σ, which are applied to the image Y ; θ is an edge measure given by:
2)
and g is the diffusion coefficient proposed by Weickert et al. [15]:
(3)
The α parameter is a threshold to control the diffusion [9]. Duarte et al. [9] showed that semi-implicit schemes can solve the nonlinear diffusion faster than by using explicit discretization. The semi-implicit discretization of the nonlinear diffusion PDE is expressed in matrix form as:
(4)
where µ is the scale step, i.e., 
is the hyperspectral image and 
is the diffusion coefficients matrix. An algorithm, to solve the hyperspectral image’s nonlinear diffusion using multigrid methods (AMG) was proposed by Duarte et al., [10] and it is used in this paper.
2.2. Binary Partition Tree
Binary Partition Tree -BPT is an image representation based on regions. BPT is mainly used for image segmentation [12], and was introduced for hyperspectral image processing in [13, 14]. Each of the tree’s levels is a partition of the image into a region. A region adjacency graph, G = (V,E), is used to represent each level. BPT is built by successively merging region operations in the region adjacency graph. The first level corresponds to an initial partition obtained by a region growing algorithm [12]. BPT requires that a merging order, a merging criterion, and a region model are all selected [12]. In this paper, a first order statistic is used as the region model, i.e. each region is represented by the spectra mean of its constituent pixels:
(5)
where V are the graph vertices, R i is a region, 𝑚 𝑖 is the number of pixels in R i , y i is a pixel in R i , and n is the number of bands. The merging criteria are established by using a similarity measure: the cosine distance. The merging order is given by the most similar regions, i.e. the regions with the minimum distance. Furthermore, building a BPT level requires a three-step process: computing the cosine distance between regions, merging the two most similar regions, and updating the region model [12, 13].
3. Scale selection
Multiscale representations build a family of images, 
, where Yi is a scale. For nonlinear diffusion, Yi a smoothed image obtained by solving eq. (1). For binary partition tree, Yi is the image build from the RAG in level i Hyperspectral image classification requires one single scale. For this reason, scale selection approaches are explored in this paper. These criteria are usually used for filtering of gray scale images. This work presents the generalizations of scale selection methods for vector-value images.
3.1. Minimal Entropy Change
Sporring and Weickert [16] used the scale that achieves minimal entropy change. The minimal entropy change is an indicator of stable scales. The entropy for a gray-scale image is given by:
(6)
where pi is the histogram count for the intensities values ranging from 1 to K. The optimal scale is found by minimizing the entropy change ΔS. Extending this criterion to a vector-value image is undertaken by using the average entropy across bands.
3.2. Decorrelation Criterion
The decorrelation criterion proposed by Mrazek and Navarra [17] used the scale for which the minimum correlation between the smoothed image in the time 𝑡, Yt, and the differential image between Yt, and the original imageY, Yt - Y, is found. It is expected that this correlation will decrease as more iterations are performed. When the smoothing operations remove significant details from the image, the correlation begins to increase. The scale for which the correlation is minimum guarantees that important details are not removed. A generalization of the decorrelation criterion for vector-value images is obtained by averaging the correlation in each band:
(7)
where Yt (i) is the band 𝑖 in the scale 𝑡 and 𝜌 is the coefficient of correlation.
3.3. Diffusion Balance Criterion
Jiabin and Guizhong [18] proposed using the scale for which the multiscale representation achieves a balance:
(8)
where EY is the energy of the smoothed image at t, and ED is the energy of the differential image 
at the scale t. The extension of the diffusion balance criterion to vector-value images is performed by using the Frobenious norm as a measure of energy.
3.4. Entropy Change
The entropy can be seen as a measure of information. As more smoothing iterations are performed, more information is removed from the image. Thus, the entropy change of is significant in the first iterations. The entropy change criterion proposed in [11] selects the scale where the entropy change achieved a break point. The perceptual difference between
T
t
and
Y
is used to generalize the criterion for any image:
(9)
4. Experiments
4.1. Dataset
The comparison of multiscale representation approaches with scale selection criteria for classification purposes was performed using the AVIRIS image, which was collected over the West Lafayette (USA) agriculture region. This hyperspectral image, named Indian Pines, has 145x145 pixels and 220 spectral bands from 400 to 2500 nm. There is a classification map with 16 classes of Indian Pines available online (https://engineering.purdue.edu/~biehl/MultiSpec/). Fig. 1 (a) shows band 42 of the Indian Pines. Only 197 spectral bands are used. Water absorption bands, 107 to 114 (1353 nm to 1422 nm) and 153 to 167 (1811 nm to 1939 nm) were removed.
4.2. Multiscale Representations and Classification
For India Pines, 20 smoothing iterations were performed using nonlinear diffusion in order to obtain a multiscale representation. The diffusion coefficient α was set equal to 0.01, and the scale step µ was set equal to 5. For the binary partition tree, an initial partition was performed with a region growing algorithm. Each level of the binary partition tree is taken as a scale. Fig. 1 (b,c) shows the 42nd band for the smoothed image with nonlinear diffusion in the third iteration and the image in the 120th level in BPT.
First, the original image and the family of images from the nonlinear diffusion and binary partition tree representations were processed using a super vector machine classifier with a second order polynomial kernel. The classification was performed using 10% of pixels as training samples. Table 1 shows the classification accuracy that was obtained for 12 images, and Fig. 2 presents the classification accuracy for all images in the multiscale representation that was obtained by (a) nonlinear diffusion and by using a (b) binary partition tree.
Source: The authors.
Figure 1 Spectral band 42 for (a) Original Image, (b) fourth iteration of nonlinear diffusion, and (c) 120th level of BPT.
Table 2 shows the classification accuracy per class obtained from the fourth iteration of nonlinear diffusion and the 120th level of binary partition tree.
4.3. Comparison Scale Selection Criteria
The scale selection criteria were compared according the classification accuracy obtained from the smoothed image selected as the optimal scale. Table 3 shows the selected scale for the decorrelation criterion (DE), the minimal entropy change (MEC), the diffusion balance criterion (DBC), and the entropy change (EC).
Source: The authors.
Figure 2 Classification accuracy for (a) nonlinear diffusion, and (b) binary partition tree.
Table 3 Selected Scale and their Classification Accuracy for Nonlinear Diffusion Representation.
Source: The authors.
For the binary partition tree representation, only the decorrelation criterion proposed by [17] obtained a unique scale. This criterion selected the 100th iteration in the BPT were a classification accuracy of 94.6% is achieved. The other methods did not provide a unique solution.
4.4. Discussion
Comparing the classification results obtained using the super vector machine from the original image and the images from the multiscale representations (Table 1), it can be seen that the accuracy increases with the latter. The best accuracy can be found in all scales from the nonlinear diffusion representation (Fig. 2(a)), and in the first 700 iterations in the binary partition tree representation (Fig. 2(b)). Scale three and four is where the best accuracy was achieved for nonlinear diffusion representation (98%). For the binary partition tree representation, the best accuracy was achieved in the 120th iteration (95.1%). Table 2 shows the accuracy improvement using the nonlinear diffusion representation. Although the binary partition tree has a better overall performance than the original image, one class is not detected by this method: BPT loses grass pasture mowed.
When scale selection criteria were compared, it was discovered that the criteria found in the literature work as expected for the nonlinear diffusion representation but not for the binary partition tree. The selected scales were different for all criteria for the nonlinear diffusion representation, as can be seen in Table 3. For the binary partition tree, only the decorrelation criterion obtained a unique solution. It is import to note that the criteria compared in this work not used labeled data, i.e. they do not require training data. All the criteria only used the information in the original image and the image family generated by the multiscale representation.
5. Conclusions
A comparison between two multiscale representation approaches was performed. Nonlinear diffusion and binary partition tree were employed to generate a family of images. The first approach was based on nonlinear filtering, in which fine details are smoothed by successively solving a partial differential equation. The second approach was inspired by region growing, and fine details are removed by a successive merging operation. A real hyperspectral image was used to compare both approaches for classification. Both nonlinear diffusion and binary partition tree representation achieved better classification performance that when the original image was used. However, nonlinear diffusion representation obtained the best overall accuracy classification as well as most of the best per class accuracy for Indian Pines.
Since the multiscale representation obtained a family of images, scale selection criteria are necessary to select an image for processing. A decorrelation criterion was enabled in order to select a unique scale for both representations. However, these selected scales did not contain the scale that obtained the best accuracy. Note that the decorrelation criterion and the other criteria do not use training data, they only used the information in the original image and the image containing the multiscale representation.
