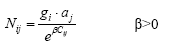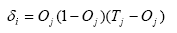1. Introducción
Los problemas de movilidad son cada vez más abundantes debido al desarrollo tecnológico de la humanidad, este gran desarrollo viene de la mano con un incremento del parque automotovilístico en las ciudades, las cuales se ven cada vez más congestionadas. Esta situación propicia excesivos tiempos de viaje, encarecimiento de mercancías, contaminación, congestionamientos, accidentes de tráfico y demandas excesivas de infraestructura para el transporte privado [1,2].
Los primeros estudios de movilidad (Mitchell & Rapkin en 1954 [3] y Alan M. Voorhees en 1955 [4]) aparecieron como consecuencia de la necesidad de regular el tráfico en las ciudades, entonces pudieron constatar una relación directa entre el número de viajes producidos entre dos zonas, el número de empleos en una de ellas y el número de residentes en la otra, así como una relación disuasoria de la distancia.
La evolución posterior de la planificación del transporte ha llevado la misma línea conceptual marcada por aquellos primitivos modelos, hasta alcanzar en la actualidad una sofisticación matemática, apoyada en gran parte por la enorme facilidad de cálculo que ha introducido la informática. Especial relevancia tienen los estudios incluidos en el ámbito de las concesiones de carreteras (Standar & Poor´s 2002 [5], 2003 [6]). Actualmente, el análisis y estudio de la demanda de movilidad cuenta ya con numerables estudios, tanto a nivel institucional como académico [7,8].
El inicio de la investigación mediante Redes Neuronales Artificiales (RNAs) aplicada al campo de la movilidad data de principio de los 90 (por ejemplo, Davalo y Naim, 1991 [9], Fakhri y Hua, 1994 [10]), como marco en el que se pueden estudiar muchos problemas de tráfico y transporte.
Las aplicaciones de RNAs en transporte son numerosas más allá del estudio de movilidad [11,12,13].
2. Objetivos
En este trabajo se describe el proceso metodológico para el estudio de la movilidad en las zonas de transporte, realizando una recopilación de los métodos de estimación de viajes. Finalmente se desarrolla un método de estimación mediante redes neuronales artificiales.
El objetivo de un sistema de transporte es diseñar una oferta adecuada a una demanda concreta. La demanda es el resultado de la necesidad de cubrir unas actividades que implican desplazamientos, con un conocimiento preciso de las distintas características que la determinan.
Para estimar la demanda futura de transporte se utilizan modelos matemáticos [14], capaces de predecir lo que ocurre con la movilidad de la población, con la finalidad de conocer los efectos que se produzcan en las redes de transporte, debido al aumento poblacional y a los cambios inducidos por la aplicación de diferentes estrategias y políticas [15].
El estudio se centra en el área metropolitana del Campo de Gibraltar y área de Málaga, constituida por siete municipios, situada en el extremo sudeste de la provincia de Cádiz. Tiene una extensión de 1.529 km2 y una población actual que supera ligeramente los 265.000 habitantes. En ella se encuentra el primer polo químico de la comunidad autonómica y uno de los más importantes puertos de Europa. Todo ello hace que el tráfico rodado de mercancías sea especialmente relevante. Málaga es la capital de la Costa del Sol y cuenta con una población de más de 700.000 habitantes con un amplio tejido de servicios orientados al turismo.
El proceso para la planificación del transporte consiste en el análisis de generación y distribución de viajes, uso modal y asignación de viajes. Previamente, se realiza el proceso de validación, que consiste en que la serie de modelos reproduzcan la situación determinada en el diagnóstico.
Las redes neuronales artificiales son una técnica de reciente aplicación consistente en un método computacional de soft computing basado en un proceso de aprendizaje que se muestran con gran potencial también en el ámbito de la ingeniería del transporte [16].
En la literatura se pueden encontrar algunos estudios aplicados al transporte dependiendo del modo de viaje, variables de entradas y del ámbito geográfico, ninguno relacionado con la predicción de la demanda de viajeros para el diseño de la red de transporte en el Campo de Gibraltar [17,18].
Este estudio consiste en desarrollar un método alternativo de predicción mediante redes neuronales artificiales y su aplicación práctica en el Campo de Gibraltar y área de Málaga.
3. Datos y área de estudio
3.1. Recogida de información
Los modelos de transporte intentan explicar cómo es la demanda de transporte, siendo un dato básico conocer ésta con la mayor precisión posible, así como las variables que la pueden explicar. Esto requiere una amplia recogida de información, en cada una de las fases de la demanda, oferta y variables explicativas.
Se recoge información sobre todos los viajes realizados por la población durante un día determinado: motivo del viaje, modos de transporte utilizados, coste del viaje, etc. Además, se suele recoger información socioeconómica: renta, ocupación, estudios, etc.
Los datos utilizados en este trabajo, tanto para los métodos clásicos se obtienen de la encuesta de movilidad en día laborable en el Campo de Gibraltar y área de Málaga [19,20].
3.2. Zonificación
El proceso de planificación del transporte ha de tener una referencia espacial, donde se localizan las infraestructuras o los servicios. Por ello, el proceso de planificación tiene una tarea previa que es la delimitación del área de estudio y su zonificación.
La tarea de zonificación pretende referenciar espacialmente los flujos de viajes y las variables explicativas.
Cada zona se denomina zona de transporte y se han de seguir los siguientes criterios para su zonificación:
Criterios de homogeneidad:
Similitud del tamaño poblacional de cada zona, que sólo ha sido alterado en determinados casos por razones muy concretas, en especial al individualizar determinadas zonas singulares con carácter especial (zonas aisladas, zonas turísticas, industriales, entidades con menor población, sectores en los que se concentran actuaciones importantes y, con un nivel de población menor).
Homogeneidad urbanística, en cuanto a calificación y usos del suelo según el planeamiento urbanístico.
Homogeneidad de la población en cuanto a características socioeconómicas.
Criterios de agregación. La zonificación adoptada respeta el seccionamiento censal, se utiliza la sección censal como unidad mínima de población. Cada zona de transporte se ha formado por agregaciones de secciones -que no tienen porqué pertenecer al mismo distrito censal- y nunca una misma sección se incluye en más de una zona de transporte ni quedado excluida.
Criterios de accesibilidad al sistema de transporte. Se busca la similitud de acceso dentro de cada zona a los ejes viarios básicos, a la red de transporte público colectivo y a los nodos o puntos de concentración de paradas e intercambio, de manera que la accesibilidad al sistema de transporte sea lo más homogénea posible en cada zona de transporte.
Criterios de límites reconocibles. Tanto para facilitar la identificación en el terreno como porque, en numerosos casos, constituyen barreras físicas que imposibilitan, o encauzan, la movilidad: cauces fluviales, líneas ferroviarias, autopistas, etc.
3.3. Matriz de movilidad
El objeto primordial de las encuestas es obtener la matriz de movilidad de la demanda de transporte entre las zonas consideradas en la zonificación [21]. La matriz de movilidad o matriz origen-destino tiene por elementos los viajes entre zonas. Cada celda ij representa los viajes generados por la zona i con destino j. Dichos datos proceden de encuestas domiciliarias. Este tipo de encuestas se realizan entrando físicamente en el hogar, son idóneas para describir la situación socioeconómica y de movilidad de un área, abordando un amplio conjunto de variables.
La Dirección General de Transporte de la Consejería de Obras Públicas y Transportes realizó en 1995 una encuesta detallada sobre la movilidad en día laborable en la comarca, que se ha ido actualizando sistemáticamente para adaptarla a la realidad actual. En conjunto se definieron 66 zonas de las que 32 son con población y 34 sin ella, establecidas a efectos de atracción de viajes (superficies comerciales, zonas industriales,...), agrupándolas en 7 macrozonas de movilidad.
Se procederá al análisis simultáneo con los datos de movilidad la encuesta en día laborable en el área de Málaga en 2011. En este caso se agrupa la movilidad en 32 macrozonas, con lo que resulta una matriz de movilidad 32x32.
Siguiendo los criterios anteriores se realiza la zonificación del Campo de Gibraltar (Fig. 1) y Málaga (Fig. 2).

Fuente: Encuesta de movilidad en día laborable en el Campo de Gibraltar en 1995.
Figura. 1 Zonificación Campo de Gibraltar.
4. Metodología
A partir de las matrices de movilidad, se trata de elaborar un modelo matemático que permita explicar el número de desplazamientos que se producen actualmente y en el futuro, entre cada par de zonas i y j, en función de los datos socioeconómicos de las zonas y de los costes de transporte, tanto en el modo m como en el resto de los modos.
4.1. Modelización clásica
4.1.1. Modelos directos
En los modelos directos [22] se integra, en una misma ecuación, los valores explicativos que se consideran en el proceso de decisión. Su fórmula general es:
Donde:
 :
:  : Variables socioeconómicas expresivas de la actividad económica en las zonas i y j.
: Variables socioeconómicas expresivas de la actividad económica en las zonas i y j.
 : costes de transporte entre i y j.
: costes de transporte entre i y j.
Un modelo simplificado de este tipo, referido a movilidad por carretera, es:
 : viajes por carretera entre i y j.
: viajes por carretera entre i y j.
 : coste de transporte entre i y j (distancia, tiempo o coste)
: coste de transporte entre i y j (distancia, tiempo o coste)
 : constantes a ajustar por regresión lineal:
: constantes a ajustar por regresión lineal:
4.1.2. Modelos secuenciales
En los modelos secuenciales, la demanda de transporte se explica a través de tres modelos:
Modelos de producción de viajes. Explican los viajes que se producen en una zona en función de variables socioeconómicas de la zona.
Modelos de distribución zonal. Explican la distribución espacial de viajes; hacia qué zonas se dirigen los viajes producidos en cada zona.
Modelos de distribución modal. Explican la elección de modo, de los viajes que se producen en una relación origen-destino, cómo se repartirán en los modos que sirven a la relación.
Este estudio se centra en la estimación de viajes entre zonas, siendo el reparto entre modos un análisis posterior.
Uno de los modelos más utilizados son los Modelos Gravitarios [23]. El flujo Nij entre dos zonas i y j, es proporcional a la generación (población) de la zona origen i, a la atracción (población, empleo, etc.) de la zona destino j y decrece con la distancia que les separa o coste de transporte
gi : generación del sector i.
aj : atracción del sector j.
F(cij) : función decreciente de la fricción, dificultad o coste de relación entre i y j.
En los modelos aplicados a un sólo modo de transporte, el factor fricción, habitualmente empleado, es el denominado coste generalizado de transporte.
tij : tiempo de viaje entre i y j.
dij : distancia de viaje entre i y j.
pij : precio del viaje entre i y j.
Mientras que si el modelo se aplica a varios modos de transporte, el factor fricción será el coste generalizado pondera.
a) Función exponencial negativa
b) Función potencial inversa
c) Función Gamma
4.2. Modelado con redes neuronales artificiales
Las redes neuronales artificiales son modelos analógicos que tiene como finalidad simular el procesamiento de información del conjunto de neuronas presentes en el sistema nervioso de los seres vivos.
En su forma más común, las redes multicapa, el funcionamiento se basa en la combinación de las variables de entrada que son transformadas mediante unas funciones de activación. Cada entrada está multiplicada por un peso. Todas las entradas son sumadas para determinar el nivel de activación de la neurona o entrada neta. Finalmente, a esta entrada neta se le suele aplicar una función de activación, por ejemplo, una función lineal, de tipo umbral, logística, etc., para obtener la salida final.
La configuración multicapa más común es la formada por tres grupos diferenciados o capas. Las unidades de entrada muestran los datos vinculados a los ejemplos presentados, las unidades intermedias (también llamadas unidades ocultas) conforman la estructura interna de la red, y las unidades de salida representan las clases a las que pertenecen los datos presentados, o los valores que se pretenden obtener como salida de la correspondencia modelada.
4.2.1. Funcionamiento de una neurona
Cada conexión entre la i-ésima unidad y la j-ésima tiene asociado un peso de conexión wij . Cada neurona tendrá un valor de entrada neto, basándose en todas las conexiones de entrada y salida.
Una red y también una neurona, son sistemas dinámicos, que evolucionan a lo largo del tiempo. Se pueden escribir ecuaciones diferenciales que describan el ritmo de cambio temporal de las salidas de las unidades:
Donde gi representa una ecuación diferencial general. Como netai depende de varias neuronas, en realidad tendremos un sistema de ecuaciones acopladas. A veces resulta interesante estudiar el vector de peso wij como un sistema dinámico:
Donde la ecuación diferencial Gi representa la ley de aprendizaje, que consiste en encontrar los pesos que codifican el conocimiento que deseamos tenga la red. Una vez aprendido este conocimiento, la red podrá utilizarse proponiendo nuevos vectores de entrada a los que el sistema responderá según lo aprendido.
4.2.2. Funcionamiento de una red multicapa
Una vez que se aplica un vector de entrada en la primera capa de unidades de red, la señal se propaga a capas interiores hasta llegar a la capa de salida. En este momento la seña de salida (real) se compara con la salida que se pretendía obtener (deseada), y se calcula una señal de error para cada unidad de salida. La señal de error se transmite hacia atrás, hacia todas las unidades que contribuyan directamente, llegando a ellas una fracción del total del error. Basándose en la señal de error recibida, se recalculan los pesos de las conexiones de cada unidad y cada capa, de tal forma que la red llegará a un estado de convergencia en el que todas las entradas les corresponderá aproximadamente su salida deseada prevista.
Esta regla de aprendizaje es conocida como blackpropagation [24], que es un tipo de técnica de optimización basada en un gradiente descendente, y que puede ser descrito por los siguientes pasos:
Inicializar los pesos y umbrales a valores aleatorios.
Se obtiene la salida de cada unidad, siendo determinadas directamente por la instancia presentada a la red. Para las unidades ocultas y de salidas el valor de la activación Oj estará estimada por (siendo F la función sigmoide):
1. El ajuste de pesos debe comenzar en la capa de salida e ir realizándose hacia atrás ajustándose los pesos (siendo ŋ el ratio de aprendizaje que debe estar entre 0 y 1):
Donde
El gradiente de error vendrá dado por:
Para las unidades ocultas (siendo δk el gradiente de error de la unidad k que dispone de conexiones con la unidad oculta j):
2. Repetir los pasos 2 y 3 si el error cuadrático medio es mayor que un cierto valor (convergencia deseada).
La función de activación elegida debe ser derivable como condición necesaria para los métodos de gradiente descendente. Así, por ejemplo, la función sigmoide tendría una ecuación:
Las reglas de aprendizaje estándar hacen que la actualización de pesos se realice en la dirección del gradiente descendente del error. Esto no produce siempre los mejores resultados por varias causas:
Convergencia a un mínimo local.
Si el gradiente es pequeño, la convergencia será lenta.
A veces la dirección contraria al gradiente no indica el camino más rápido para llegar al mínimo.
Los pesos toman los valores muy grandes, y la red no se actualiza ya que hay saturación en las unidades. Esto se denomina parálisis de la red.
Para intentar salvar las deficiencias anteriores se ha utilizado el algoritmo de Levenberg-Marquart [25].
Algoritmo de Levernberg-Marquart
La idea fundamental es no tener que calcular la matriz Hessiana, al igual que en los modelos Quasi-Newton. Si el criterio a minimizar es una función de error basada en una suma cuadrática de errores, el Hessiano se puede aproximar por el espacio H=JTJ, donde J es el Jacobiano de la función criterio. El Jacobiano contiene las primeras derivadas con respecto a los pesos. El gradiente podría ser calculado como JTe , donde e son los errores. Entonces el algoritmo de Levernberg-Marquart usa esta aproximación para conseguir una regla de actualización de los pesos como:
Si µ es 0, el método se convierte en el método de Newton con aproximación del Hessiano. Cundo µ es grande, se parece más al gradiente descendente. Como el método de Newton es más rápido y seguro, lo mejor es tender hacia él lo antes posible.
5. Diseño experimental. Resultados
En este apartado se procede al cálculo práctico de la demanda de transporte entre zonas de movilidad.
5.1. Consideraciones iniciales
Tanto en la Encuesta Domiciliaria en el Campo de Gibraltar como en el Área de Málaga contabilizan los desplazamientos que realizaron los residentes durante un día laborable medio desde un origen a un destino, con un motivo concreto, con independencia del número de medios (o etapas) que se hayan realizado en el desplazamiento.
En viajes de movilidad obligada (trabajo y estudios) se han contabilizado la totalidad de viajes, mientras que en los de movilidad no obligada se han contabilizado los
realizados en medios mecánicos y los realizados a pie que tengan una duración superior a 5 minutos.
La información está referida a los desplazamientos realizados por todos los miembros de la unidad familiar (mayores de 5 años) el día anterior al de la encuesta. También se incluye a los transeúntes. No se han considerado los viajes realizados a pie en su totalidad siempre que su duración fuese inferior a los quince minutos y el motivo fuera distinto del trabajo o los estudios.
El tiempo del desplazamiento medio en ámbito urbano en España es de 25 minutos y la distancia del viaje medio de 7,1 kilómetros [26].
Tabla 1 Variables socioeconómicas según el modelo clásico. Comparativa entre los valores resultantes de los métodos clásicos.

Fuente: Elaboración propia.
Utilizando los datos explicados anteriormente, se ha diseñado un experimento de remuestreo aleatorio con el objetivo de garantizar la aleatoriedad y la robustez de los resultados.
5.2. Diseño mediante métodos clásicos
Para modelar las ecuaciones de los modelos clásicos de estimación de viajes se utiliza el software Matlab. Tanto el método directo como los métodos gravitatorios descritos se modelan mediante regresión múltiple lineal. En estos métodos se descartan los valores de movilidad nulos al hacer logaritmos neperianos para la regresión lineal. Sea la ecuación general siguiente:
Siendo Y el valor de movilidad entre dos zonas y X1 y X2 variables socioeconómicas definidas por el modelo (Tabla 1).
Los valores experimentales resultantes se muestran en las Tablas 2 y 3.
Tabla 2 Valores experimentales modelos clásicos Campo de Gibraltar. Coeficiente Correlación

Fuente: Elaboración propia.
Tabla 3 Valores experimentales modelos clásicos Área de Málaga. Coeficiente Correlación

Fuente: Elaboración propia.
Con los datos disponibles y los resultados obtenidos se deduce que el Modelo Directo es el método que mejor explica la movilidad. Aunque hay que tener en cuenta que los resultados son bastante pobres pues el coeficiente de correlación, R, mayor es de 0,48 en el caso del Campo de Gibraltar y de 0,30 en el área de Málaga.
5.3. Diseño mediante redes neuronales artificiales
Las redes neuronales artificiales permiten el uso de múltiples variables. En un primer análisis, y con el objetivo de poder comparar con los métodos clásicos, se toman las mismas variables socioeconómicas anteriores. Las capacidades para modelar correspondencias no lineales entre entradas y salidas están bien ilustradas en Hornik et al [27], si bien no se puede determinar a priori el número de unidades-capas ocultas o intermedias. Por ello, los autores previamente han diseñado y utilizado con éxito en diversos trabajos un procedimiento de remuestreo aleatorio para determinar el número óptimo de unidades para resolver un problema [11-13].
Mediante el software Matlab y su toolbox de Neural Networks se procede al entrenamiento de la función. Una vez comienza el entrenamiento, este acaba cuando se llega a cumplir alguno de los siguientes puntos:
El error cuadrático medio de los valores de entrenamiento se fija como objetivo a cero.
El número de iteraciones máximas es 100.
µ es igual o mayor a 1E10.
El gradiente de la función error es menor o igual a 0,01.
Realizando 30 repeticiones utilizando el mencionado procedimiento de remuestreo aleatorio (toma aleatoria de subconjuntos de datos) con las variables por defecto (20% valores de validación, 20% valores de test y 60% valores de entrenamiento) se obtiene un coeficiente de correlación Rmedio de 0,81691 para el Campo de Gibraltar y de 0,89669 para el Área de Málaga.
Los resultados obtenidos con los datos utilizados son claramente superiores a los obtenidos con los métodos clásicos, puesto que el coeficiente de regresión, R, es claramente muy superior a 0,30 (Tablas 2,3).
6. Conclusiones
Para finalizar este estudio se pueden definir las siguientes conclusiones:
Los métodos gravitatorios clásicos no modelizan bien la movilidad en la zona de estudio, resultando coeficientes de correlación lineal bastante lejanos a la unidad.
Las redes neuronales artificiales obtienen un diseño de movilidad bastante cercano a la realidad, con valor de coeficiente de regresión cercano a la unidad. Además, permiten la utilización de otras variables socioeconómicas que podrían afinar aún más el ajuste.