English (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
1. Introduction
Gamification have been defined as a process which shapes the world (achieves goals/objectives) by influencing the actions, behaviours, characteristics and state of entities within the world through the use of games strategies and enabling technologies [1]. The concept is relatively new, but it has gained considerable interest in the software development and user interface design community over the last few years. The roots of gamification are in game design, with some elements from psychology, so there are still little academic research how to design and develop software systems with and for gamification.
According to Gartner Inc. [2], the widespread interest that gamification has been attracting recently lies in its potential to strengthen engagement, change user behaviours and support innovation. Game theory based models are being widely adopted now in different contexts and used as a driver for solving problems in a wide variety of domains, including disaster management [3], education [4,5], e-learning [6], workplace improvement [7], marketing [8], healthcare management [1,9], IT service management [10], social policy [11], sports and fitness [12], tourism business [13], customer engagement, social missions, fostering creativity, employee and management training, etc.
The underlying concept of gamification is motivation. Gamification is driven primarily by the external motivation, i.e., the users strive to compete against other playing users and to get recognized by the game community [12]. As motivation tends to decay over time, it however must be supported by the increasing complexity and evolving dynamics of game mechanics [14]. Meaningful gamification (otherwise known as “serious game”) is the use of game design elements to help users find meaning in a non-game context. Rather than just using game mechanics to give points or badges to users as external rewards, meaningful gamification focuses on the playing process (aka game mechanics) itself in order to engage the players to do meaningful tasks in a real world.
The modelling of gamification is important for design of systems based on the principles of serious game in order to quantify and validate the impact of gamification and to get a better understanding why and how gamification works. Existing evaluations of gamification usually focus on using user questionnaires and other methods of qualitative evaluation. There is still lack of high-level formal or abstract modelling methods and tools to aid the design and development of gamification in serious systems.
This paper aims to introduce tools which would allow to build a bridge between formal modelling of gamification and quantitative simulation of games, analysis and evaluation of game rules and processes.
The structure of the remaining parts of the paper is as follows. The overview of gamification models and gamification modelling languages is presented in Section 2. Similar formal approaches to game design are considered in Section 3. Formal description of the proposed UAREI (User-Action-Rule-Entities-Interface) model is given in Section 4. The visual notation used for modelling is described in Section 5. A case of study is presented in Section 6. The evaluation is given in Section 7. Finally, the conclusions are presented in Section 8.
2. Gamification models and modelling languages
In game research there is a strong separation between design methodologies and usability evaluation tools, which are rarely employed in the early stages of the design process. Although the game developers use many often heuristically designed tools to assist the design, there is still very little existing methods employed to connect design practices with gamification and game design [32]. Currently game and gamification development is strongly related to the qualifications and skills of game designers. This limitation drives the need to better and faster game building. Recently several new tools were developed or adapted to help game designers to model, build and analyses games.
Unified Modelling Language (UML) is a de-facto standard modelling language used in multiple domains. Tenzer [15] argues that UML modelling tools could be also used to build games and proposes a framework for building games using UML. The advantage of UML is that it is well known in the software engineering community. SysML is a general-purpose modeling language for systems engineering applications. That supports specification, analysis, design and verification of a broad range of systems. SysML has been used for building a training game [16].
The most notable examples of domain-specific game description languages are GaML [17,18] and ATTAC-L [19]. GaML is a formalized language for specifying and automatically generating gamification solutions. This allows to free the IT expert from the generation of gamification solutions. ATTAC-L is a domain specific language which allows the user to specify the game scenario in XML and to build a game using a code generator.
Another approach to gamification modelling is based on using formal (or mathematical) models [20]. Kim and Lee [21] model the effectiveness of gamification effectiveness using a mathematical model based on a sigmoidal equation. They argue what gamification effectiveness can be represented using curiosity, challenge, fantasy and control factors. Bista et al. [22] have proposed the first formal gamification model. Chan et al. [23] offer a similar approach for social game modelling, which also allows for verification of the built model. Oliveira et al. [24] model games using Petri nets. The disadvantage of this approach is the lack of domain specificity which is preventing its adoption by game designers.
The third category of gamification modelling approaches is visual languages for fast prototyping in gamification domain. Most known examples are Sketch-It-Up [25], Ludocore [26], and Machinations [27]. Sketch-It-Up is a tool for creating sketches of possible games. Ludocore is a logical “game engine”, which employs formal logic used by automated reasoning tools in AI domain to enable automated design and prototyping of game systems and providing fast feedback to the designer. Machinations is a conceptual framework and diagram tool that focusses on structural qualities of game mechanics. Machinations graphical diagrams are an abstraction of Petri nets for modelling and simulating games and game-like systems on a varying level of abstraction. Recently, Micro-Machinations [28] were proposed for reusing Machinations models in software development.
3. Formal models of game design and gamification
Games are a kind of systems and the design of games is the creation of models for games [33]. In computer science, games can be considered as a kind of information systems consisting modelled using of objects (or entities, concepts), attributes (properties), their relationships and the environment (or context) [37]. A similar approach has been adopted by ontology engineering [34] for building ontologies, i.e., formal representations of concepts within a domain and the relationships between those concepts.
Formally, games can be modelled as abstract control systems [35] consisting of a set of states and a definition of the evolution of the state of game under different actions of a player. The game can be represented by a set of states, for which transition functions define when to move from one state to another. Following this approach, gamification can be described as the product of two games, where a gamified system is considered as one game with its one rules and mechanics, and the gamification layer is considered as another game.
Another game modelling framework presented in [36] incorporates structural, temporal and boundary frameworks (subsystems). The structural subsystem consists of Game Elements, Game Time, Players, Interface and the Facilitator, the arbitrating entity between the players and the game system, which takes care of setting up the game, synchronises the game state and maintains the game time. The temporal subsystem represents the flow and causality of the game by defining the actions that are provided and the actions that can be taken at the particular states in the game. The boundary subsystem defines the constraints in the game that limit the activities performed in a game by establishing social contracts between the players which have to be satisfied while playing through a set of limitations.
In [38], another kind of formal model (Petri Nets and Hypergraphs) are investigated and methods and tools for the integration of formal modelling into the game design and production process are proposed.
These efforts in formal game modelling are however directed at game design rather than gamification of the existing systems as considered in this paper. In the following Section, the elements of the proposed UAREI model are presented.
4. Description of gamified systems as UAREI model
The gamified systems can be described as a tuple G ={U,A,R,E,I} , here: U - users, which are interacting with the system; A - actions, which trigger system behaviour; R - rules, which encapsulate logic in the system; E - data entities; and I - interfaces which define data format.
The users are defined as a tuple U ={ LU,SU }, here: LU - a set of all outgoing links to other elements in the model; and SU - a selection function which defines how a user is selected from a collection in a simulation mode.
Actions are a collection A ={ A1, A2, …, Ai, …, An }, here Ai is a single action, n the total number of actions. A single action is defined as Ai ={ LA,SA }, here: LA - a set of all outgoing links to other elements in the model, and SA - a selection function, which defines the way an action related data entity is selected from a collection.
Rules are a collection R ={ R1,R2 , …, Ri , …, Rn }, here Ri is a single rule, n the total number of rules. A single rule is defined as Ri = { LR,Ri (C,M)}, here: LR - a set of all outgoing links to other elements in the model, and ri (C,M) is a rule function defined as:
here: C - context of current execution path; M - a system model; y is a computed result value, and NULL is returned if rule doesn’t apply.
Rules are used to control context flow in the system. If a rule execution evaluates to an empty result the current execution path is continued. We can define the “else” path by using inversion “! Ri ”. No data will be stored in storage and no other rules will execute if the previous rule failed or returned empty value, but system flow will continue giving feedback to the user node. Rules can update the context in anyway needed for the application.
Entity collection is a collection of all data entities in the system 
, here Ei is a single storage entity and n is the total number of storage entities. A single entity is defined as 
here: D- entity scheme definition, O - data objects, and L
E
- a set of all outgoing links to other elements in the model.
Interface is a collection 
, here Ii is a single interface and n is the total number of interfaces. A single interface is defined as Ii = {LI, Q}, here: LI -a set of all outgoing links to other elements in the model, Q - data query, on which the data for the interface is selected.
5. Graphical notation of UAREI model
The UAREI model is visualized as a directed graph consisting of nodes (vertices) and links (edges) between nodes as follows: G ={L,N}, here: N is a set all nodes N = 
; is a set of links between nodes 
, and 
are collections of corresponding types of nodes 
, Li is the list of links, Li = (Nout; Nin), here, 
- are links which start N
i
node.
In Table 1 we present the list of graphical symbols (graphemes) used in the UAREI model diagrams.
6. A case of study in modelling gamification in Trogon PMS
For the illustration of gamification modelling, we have selected the Trogon Project Management System (PMS) already discussed in our previous work [29,30]. Here we demonstrate how gamification rules can be described and modelled using the proposed UAREI model as well as depicted graphically using the proposed graphical notation. The gamification solution for Trogon PMS is defined as follows:
A software company employee receives random stream of tasks is coming from the project manager. There are two main types of tasks - normal tasks and tasks with badges. There are nine distinct types badges rewarded based on the tickets specificity. Everything translates to points, a certain amount of points is awarded per task done. Based on the number of badges of the same type a bonus is awarded. For every task completed with a badge a user gets 20% bonus. When five and more of the same type badges are collected for those tasks the user is awarded with an additional 20% bonus. There is a quality element to the tasks done, if the task fails to pass Quality Assurance, a badge can be removed.
The Trogon PMS gamification is defined using the UAREI model as follows:
here:
In order to be made executable, a formal model has been converted into a JSON notation. This is done by writing down a JSON structure, which is composed of two parts (model nodes and model name). Every model node follows main format of name, type and links. Rules are generated by interpreting a meta-language represented as a JSON structure. The language has 1 to 1 translatable language constructions like conditions, iterations, logical operations, mathematical operations and other. Next to this the meta-language has code structural constructs. The language can be extended with necessary element to support required features.
The model of gamification of Trogon PMS using the UAREI modelling language is given in Fig. 1. The model contains:
Entities: E user - all system employee, E Badges - types of badges, E Tasks - the tasks which can be completed by employees, E Points - points gained by the users.
Users (U employee ) node which is a starting point for interaction with the system.
System has only a single action (A finish task ) which is triggered by system users when a task is completed.
System has two main rules: the Points rule (R recieve badge ) describes normal behavior how user receives the points for a completed task, and the Badge rule (R recieve badg ) describes how user gets points for finished tasks which have badges associated with them.
For comparison, the UML diagram which represents the same logical flow is given (see Fig. 2) as well as the same model described using the Machinations visual notation (Fig. 3).
User feedback loop is finished by leader board interface (I leaderboard ), which gives relevant feedback to the user.
As the UAREI model is described using the elements of the graph theory, we use the graph metrics to evaluate its visual complexity: number of nodes N, number of links E, and McCabe Cyclomatic Complexity defined as
M=E-N+2∙P,
here P is the number of independent paths in a graph.
The complexity of the UAREI and Machinations gamification models of Trogon PMS is summarized in Table 2. The comparison results show that the UAREI model is significantly less complex than its Machinations counterpart.
Source: created by the authors
Figure 2 Gamification model of Trogon PMS specified using UML activity diagram.
The computational simulation results of the proposed gamification model are presented in Fig. 4. The UML activity model is not illustrated, because UML has no simulation engine.
We assume that the system has two players (‘Blue’ and ‘Red’) with exactly the same behaviour competing at the same time. Fig. 4 shows the data recorded during such simulation.
There are two distinct parts of the simulation:
Tie zone - from the start models are behaving similarly and both players have a similar number of points.
Winner zone - one of the players starts winning and the other player needs time to close the gap.
Both players can become the winner because:
At the core of these models is a binomial distribution of a fare coin, so any player can win based on luck, while no player specific attributes are taken into consideration.
The winner is only determined, because we stop the model at a certain time limit. In case the model goes to infinity we would end up in a tie state.
There is some difference in the simulation data, because of different simulation execution and model specifics. In case of Machinations, a tick is executed every time the resource passes from node to node, and in the UAREI model a data record in point entity triggers a data point in the graph.
7. Evaluation
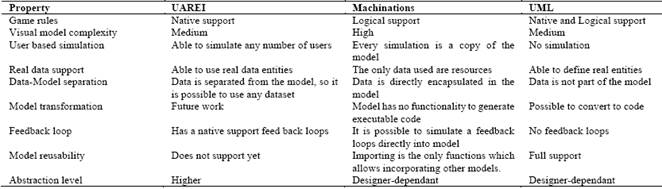
For comparative evaluation, we use the Machinations visual language [27]. As comparison criteria we use the most important problems / attributes in gamification modelling.
The game rules are supported in both UAREI and Machinations. The main difference is that Machinations only allow to build a logical structure to imitate the “rule” concept. UAREI natively supports the rule concept. Rule in the model holds the logic inside it and not disclosing its logic in model visualization. This is a main difference between these two modelling tools. The biggest problem in Machinations is that model complexity grows exponentially if one tries to model real world systems. In UAREI, most of the game logic is encapsulated in rules which decreases model complexity.
Both modelling frameworks support user-based modelling. However, in Machinations every user behaviour model has a separate copy of the model. UAREI natively supports multiple users working with the same model in parallel. Machinations currently support logical attributes which describe user behaviour. UARSEI currently does not have such modelling capacities.
Source: created by the authors
Figure 3 Gamification model of Trogon PMS specified using Machinations.
Machinations is based on the economic functions and the resource concept. UAREI natively focuses on real data entities which carry more information. UAREI has the “context” concept which is carried through the model execution flow. In general, the context concept of UAREI is similar to Machinations resource concept.
UAREI supports real world data entities and that allows mapping into software domain. UAREI separates actual data from the actual model. Normally in software engineering this is a common way to ensure data-program separation, the same concept is encapsulated into UAREI. Machinations does not have a concept of data.
Machinations does not have any model transformation capabilities and it never was designed for this goal. On the other hand, UAREI is designed for transformation into executable code. The rule logic is written in a meta-language which is processed into executable Javascript code. Other model parts are executed using a simulator.
Both UAREI and Machinations have minimal analysis tools which allow to view model data. In Machinations one is able to view “pool” changes over time. In UAREI one is able to see interface data change over time.
UAREI has a native feedback loop in the system. The modelling framework is designed to ensure feedback to model users. In Machinations it is up to designer to setup such loop to model user behaviour during simulation.
8. Conclusions
In this paper we have presented the description of the UAREI modelling framework. We have demonstrated a case of study in modelling the Trogon PMS gamified application using UAREI. The same gamified application was modelled using the Machinations framework and UML activity diagrams. All modelling frameworks are good tools for modelling gamification of software systems.
All analysed models were used to compare their visual complexity. We run a sample simulation of two players using the system under UAREI and Machinations. The comparison disclosed the benefits and weakness of the modelling frameworks in question as follows.
The advantages of the UAREI model are a high level of abstraction, native support for feedback, model transformation to executable code, explicit separation of data and code. The disadvantage of the UAREI model is that currently it still does not support reusability.
Future work will focus on improving properties of the UAREI model in supporting model transformation, analysis and reusability.
