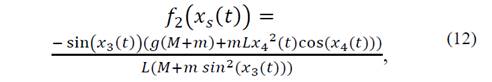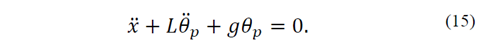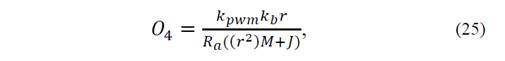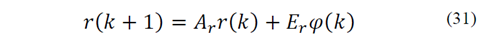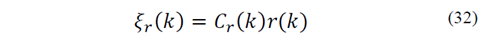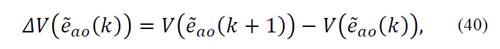1. Introducción
Las grúas torre de pluma horizontal son sistemas mecánicos encargados del transporte y posicionamiento de carga pesada dentro de una área de trabajo determinada. Las técnicas modernas de construcción emplean mayores requerimientos tanto de velocidad de transporte y posicionamiento de la carga como de precisión. Sin embargo dados esos requerimientos y considerando la configuración mecánica que presenta este tipo de sistema, se generan oscilaciones indeseadas en la carga aumentando el tiempo de posicionamiento de la misma [1], arriesgando la integridad del sistema [2] y el personal en el área de construcción.
Las grúas torre de pluma horizontal se componen de tres grados de libertad (GDL): rotación, elevación y traslación. Estos GDL son posibles gracias al movimiento en conjunto de subsistemas como la torreta, guaya (cuerda) y carretilla (ver Figs. 1 y 4). Uno de los problemas más comunes en el control manual de una grúa torre son las oscilaciones de la carga producto de perturbaciones externas como (fuerzas eólicas, sismos, etc.) o internas dado cambios de velocidad de la carga debido al movimiento en la carretilla (inercia). Estas perturbaciones obligan al operario a inhabilitar el mecanismo para evitar el aumento en las amplitudes de las oscilaciones en la carga [3]. En este sentido, la aplicación de técnicas de control ha tomado gran importancia en el campo de las grúas-torre para alcanzar requerimientos deseados en términos de desplazamiento de la carga sin generar oscilaciones de alta magnitud.
Las técnicas de control han tomado dos principales direcciones. Por un lado, esquemas de control para generar trayectorias deseadas de la carretilla que a la vez reducen las oscilaciones en la carga [4,5]. Por otro lado, teoría de control enfocada en controlar directamente la oscilación y el posicionamiento de la carga. En esta segunda dirección, investigadores se han centrado en sistemas de control, con los que obtienen movimientos rápidos y precisos en el desplazamiento de la carretilla sin generar oscilaciones considerables en la carga [6,7], sin embargo demandan modelos matemáticos detallados y no utilizan el conocimiento de las perturbaciones a las que está sometido el sistema. Además, se han propuesto esquemas de control no lineal [8-10] cuyas leyes de control resultan ser complejas, son totalmente diseñadas en tiempo continuo y en el caso de [8], se emula la perturbación del viento como una señal que no refleja de forma adecuada las condiciones a las que estaría sometida la carga durante su desplazamiento.
Bajo un enfoque diferente, en [11] se propone un controlador por rechazo activo de perturbaciones (ADRC) para controlar la posición de la carretilla y reducir oscilaciones en la carga. ADRC es una metodología de control para sistemas lineales y no lineales que fue inicialmente propuesta por Prof. Han, y luego adoptada y extendida por Prof. Z. Gao [12,13] la cual plantea estimar las perturbaciones externas e internas del sistema, asumiendo un modelo interno aproximado de la perturbación, para luego rechazarlas en línea mediante la ley de control. Actualmente, ADRC es un campo de fuerte investigación cuyas aplicaciones van desde control de motores [14], control de sistemas de potencia [15], control de robots [16], hasta control de turbinas eólicas [17]; pero muy poco explorado en el control de grúas torre. La aplicación de ADRC en [11] ha mostrado las ventajas de esta técnica, sin embargo aún hay varias desventajas que pueden ser resaltadas, a saber: el esquema de control se propone en tiempo continuo, el modelo interno de la perturbación usado para extender el observador de estados usa un aniquilador que asume que la perturbación es una señal constante, y no se muestra validación experimental de la propuesta de control que verifique la robustez y el desempeño real.
En este artículo, se propone un esquema de control basado en la filosofía del rechazo activo de perturbaciones cuya ley de control es definida en tiempo discreto, donde el conocimiento de la perturbación es mejor explotada al incorporar un aniquilador resonante dentro del observador de estados extendido que sirva para atenuar la oscilación de la carga con mejor desempeño. Además, esta propuesta de control es validada experimentalmente en una grúa-torre a escala, donde se muestra su real desempeño y robustez.
Este artículo está organizado de la siguiente forma. El modelo matemático de una grúa-torre se describe en la sección 2. En la sección 3 se describe y formula la propuesta de control. La sección 4 muestra brevemente otras técnicas de control usadas para propósitos de comparación. El análisis de robustez del esquema de control propuesto se desarrolla y discute en la sección 5. En la sección 6 se presenta la validación experimental de la propuesta de control evaluada sobre una grúa-torre a escala, considerando pruebas de rechazo de perturbaciones y posicionamiento de la carga. Por último, en la sección 7 se presentan las conclusiones del trabajo.
2. Modelo matemático de una grúa-torre fija
En esta sección, se presenta el modelo matemático de una grúa-torre teniendo en cuenta su parte mecánica y mecatrónica. Inicialmente, la parte mecánica del sistema es abordada con un análisis de LaGrange, obteniendo un modelo no lineal que posteriormente es linealizado dado un punto de equilibrio. Luego, la parte mecatrónica del sistema es agregada al sistema linealizado, para luego discretizar el modelo completo del sistema.
El mecanismo estudiado de la grúa-torre se compone de tres principales subsistemas que son: motor, carga y carretilla, en donde la carga con masa m, está acoplada directamente a la carretilla que tiene masa M ambas en Kg, por medio de una cuerda (o guaya) con longitud L en metros, y a su vez la carretilla está acoplada por medio de un juego de poleas de radio r a un motor DC, el cual es el encargado de aplicar un par ( 𝑚 para generar movimientos lineales en la carretilla. El motor es controlado por medio de un driver de potencia, el cual es modelado como una ganancia 𝑘 𝑝𝑤𝑚 que convierte ciclo útil de una señal por modulación de ancho de pulso en la entrada del driver a voltaje promedio aplicado en los terminales del motor.
El modelo estudiado describe la posición angular de la carga θp(t) en radianes respecto al eje vertical que acompaña a la carretilla. La carretilla es halada por una tensión T 1 a lo largo de un soporte, generando un desplazamiento lineal x(t)
en metros; la Fig. 1 detalla el diagrama del sistema antes descrito. El modelo considera las siguientes suposiciones, a saber: la carga es modelada como una partícula, la fricción del sistema y la masa de la cuerda son despreciadas, los movimientos de la carga y carretilla están restringidos al plano (x-y) y la cuerda es considerada como un cuerpo rígido. Estos supuestos, se consideran para obtener un modelo simplificado del sistema mecánico, despreciando dinámicas pero tomadas como incertidumbres y que posteriormente son toleradas por el esquema de control propuesto.
El modelo mecánico de la grúa-torre, se obtiene a partir de la siguiente ecuación de LaGrange [18].
donde i = 1,2, K es la energía cinética del sistema, P es la energía potencial del sistema, 𝑞 𝑖 describe la coordenada generalizada que indica la posición lineal de la carretilla x(t) y la posición angular del péndulo θ p (t) respectivamente, y 𝑇 𝑖 describe la fuerza externa que se aplica al sistema con T 1 (t) la tensión aplicada a la carretilla y T 2 =0 que define una fuerza aplicada a la masa de la carga. Entonces, de acuerdo con las suposiciones antes mencionadas, la energía cinética del sistema (ver Fig. 1), está dada por:
donde 𝑣 es un vector que comprende la velocidad de la carga dadas sus componentes vectoriales v x y vy; dicho vector está definido como:
donde  y
y . La energía potencial total del sistema está dada por:
. La energía potencial total del sistema está dada por:
donde 𝑔 es la aceleración gravitacional. Luego, a partir de la combinación de ec. (2)-(5), y teniendo en cuenta la formulación de LaGrange ec. (1), se obtiene el siguiente sistema no lineal en espacio de estados de la grúa-torre:
donde 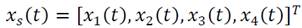 ,
,  ,
,  es la velocidad de la carretilla,
es la velocidad de la carretilla,  ,
,  es la velocidad angular de la carga, 𝑢 𝑓 𝑡 = 𝑇 1 (𝑡) es la fuerza aplicada a la carretilla, y f
i
y b
i
son funciones no lineales descritas por:
es la velocidad angular de la carga, 𝑢 𝑓 𝑡 = 𝑇 1 (𝑡) es la fuerza aplicada a la carretilla, y f
i
y b
i
son funciones no lineales descritas por:
Tomando el punto de equilibrio  , se linealiza el modelo de la grúa ec. (6)-(9), obteniendo la siguiente representación:
, se linealiza el modelo de la grúa ec. (6)-(9), obteniendo la siguiente representación:
Por otra parte, considerando solo la parte mecánica de la dinámica de un motor de corriente continua, se obtiene la siguiente representación lineal:
donde 𝐽 representa el momento inercia del eje del motor, B es el coeficiente de viscosidad del motor, kb constante mecánica del motor, θm representa la velocidad angular del motor, Vin es el voltaje aplicado en terminales del motor y τm el par del motor. Además, las ec. (14)-(15) están linealmente relacionadas con las ec. (16)-(17), mediante:
Reemplazando ec. (18)-(19), en el modelo del motor DC ec. (16)-(17) y posteriormente reemplazando en el modelo mecánico de la grúa-torre ec. (14)-(15), se obtiene la siguiente representación en espacio de estados:
con,
donde,
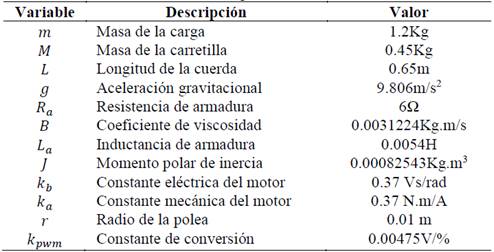
kpwm es la constante de conversión de ciclo útil a voltaje aplicado al motor, y 𝑢(𝑡) es la entrada de control que representa ciclo útil. La Tabla 1 muestra los parámetros del modelo de la grúa-torre.
Por último, el modelo matemático de la grúa-torre ec.(20) es discretizado por el método ZOH (Zero Order Hold) con un tiempo de muestreo de 𝑇 𝑠 =0.01𝑠. El modelo matemático en tiempo discreto se describe como:
donde  es el vector de estados en tiempo discreto del sistema, v(k) es la velocidad lineal de la carretilla, ωp(k) es la velocidad angular del péndulo, y
es el vector de estados en tiempo discreto del sistema, v(k) es la velocidad lineal de la carretilla, ωp(k) es la velocidad angular del péndulo, y  ,
, 
3. Esquema de control propuesto
El esquema de control propuesto se enfoca principalmente en mejorar la estimación de las variables de estado y las perturbaciones a las que está sometido el sistema, en especial las provenientes de la oscilación de la carga que en general se componen principalmente por la frecuencia de oscilación pendular de la carga que puede ser ocasionada por perturbaciones externas o internas como la inercia del propio sistema cuando la carretilla se está posicionando. Para lograr esto, el observador de estado extendido usado convencionalmente en ADRC es modificado para incluir un modelo interno que describe una señal armónica con frecuencia 𝜔 𝑟 (también llamado resonador). Luego, las estimaciones de la perturbación y las variables de estado, se usan en la ley de control para rechazar en línea la perturbación y acomodar la dinámica de lazo cerrado, respectivamente.
Entonces, como es típico en estrategias de control bajo la filosofía ADR, las perturbaciones que afectan al sistema se asumen de forma unificada a la entrada de la planta, en este caso como 𝜉 𝑟 (𝑘), y por lo tanto el sistema toma la siguiente descripción:
Donde ξr(k) es la señal de perturbación unificada la cual se desea estimar y rechazar, y está compuesta por perturbaciones externas y dinámicas del sistema generadas por incertidumbres en el modelo.
3.1. Observador de estado extendido resonante
El propósito del observador es estimar la perturbación 𝜉 𝑟 (𝑘). Esta perturbación puede ser una señal compleja de estimar, dependiendo de qué componentes de la señal deberían estimarse de forma precisa. En este caso, una componente de la perturbación debería ser muy bien estimada, la frecuencia fundamental de oscilación de la grúa-torre. Entonces, con el fin de proporcionar una estimación precisa de este componente en la perturbación y los estados del sistema, el modelo interno del observador debe contener el aniquilador de ese componente de interés, i.e. el aniquilador de una señal sinusoidal con frecuencia 𝜔 𝑟 . Por lo tanto, la aproximación del modelo interno de la señal 𝜉 𝑟 (𝑘), puede ser formulada como [19]:
donde ωr es la frecuencia de oscilación pendular de la carga en rad/s y se puede calcular usando:
con 𝑔 la aceleración gravitacional. Note que ec. (29) corresponde al aniquilador de una señal sinusoidal con frecuencia ωr, entonces el modelo interno ec. (29) provee rechazo de perturbaciones cuando  , con ∝ cualquier constante finita.
, con ∝ cualquier constante finita.
Basado en el modelo interno ec. (29) de la señal de perturbación ξr(k), se encuentra una descripción en espacio de estados dada por:
donde  . Ahora, el modelo interno de la perturbación ec.(31)-(32) se usa para construir un modelo de estado extendido que incorpore también los estados de la planta ec. (27), así:
. Ahora, el modelo interno de la perturbación ec.(31)-(32) se usa para construir un modelo de estado extendido que incorpore también los estados de la planta ec. (27), así:
donde  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  y
y  . Note que la matriz Cdo indica que las variables medidas son x(k) y θp(k).
. Note que la matriz Cdo indica que las variables medidas son x(k) y θp(k).
Con el fin de proponer el observador y la ley de control, considere la siguiente suposición respecto al modelo interno de la perturbación. Existe una constante finite Kξ, tal que,
donde,
Proposición 1 (Observador de estado extendido resonante): La estimación de la función de perturbación  , y las estimaciones de las variables de estado de la grúa-torre
, y las estimaciones de las variables de estado de la grúa-torre 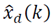 , son obtenidas por el siguiente observador:
, son obtenidas por el siguiente observador:
donde  , 𝑥 𝑎𝑜 𝑘 = 𝑥 𝑑 𝑘 𝑟 (𝑘) 𝑇 es el vector de estados estimados del observador y 𝐿 𝑎𝑜 es la matriz de ganancias del observador. Entonces, las trayectorias del vector del error de estimación
, 𝑥 𝑎𝑜 𝑘 = 𝑥 𝑑 𝑘 𝑟 (𝑘) 𝑇 es el vector de estados estimados del observador y 𝐿 𝑎𝑜 es la matriz de ganancias del observador. Entonces, las trayectorias del vector del error de estimación  , convergen globalmente hacia una vecindad de cero donde permanecen últimamente acotadas, siempre que la matriz de ganancias del observador Lao, se seleccione tal que los valores propios de la matriz (Aao-LaoCao) se ubiquen dentro del círculo unitario del plano complejo
, convergen globalmente hacia una vecindad de cero donde permanecen últimamente acotadas, siempre que la matriz de ganancias del observador Lao, se seleccione tal que los valores propios de la matriz (Aao-LaoCao) se ubiquen dentro del círculo unitario del plano complejo  .
.
Demostración 1: La dinámica del error de estimación eao(k) se puede obtener restando ec. (37) de ec. (33):
con 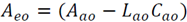 . Entonces, los valores propios de Aeo se pueden ubicar arbitrariamente por medio de la matriz Lao, tal que se ubiquen dentro del círculo unitario del plano complejo
. Entonces, los valores propios de Aeo se pueden ubicar arbitrariamente por medio de la matriz Lao, tal que se ubiquen dentro del círculo unitario del plano complejo  . El error de estimación
. El error de estimación  está restringido a una vecindad cercana al origen en el espacio de las variables de estado del error de estimación. El tamaño de la vecindad está relacionado con el tamaño del término
está restringido a una vecindad cercana al origen en el espacio de las variables de estado del error de estimación. El tamaño de la vecindad está relacionado con el tamaño del término
Para estudiar el acotamiento último, considere la función candidata de Lyapunov  , con P una matriz positiva definida. Entonces,
, con P una matriz positiva definida. Entonces,
luego de algunas manipulaciones, se concluye que:
Considerando que  es diseñada estable, y dada una matriz simétrica positiva definida Q, existe una matriz simétrica definida positiva P , tal que:
es diseñada estable, y dada una matriz simétrica positiva definida Q, existe una matriz simétrica definida positiva P , tal que:
Por lo tanto, ec. (41) resulta en:
Dado que  , asumiendo
, asumiendo  , y aplicando la suposición en ec. (35), la función
, y aplicando la suposición en ec. (35), la función  satisface:
satisface:
Resolviendo la ecuación cuadrática en  del lado derecho de ec. (44), se encuentra que
del lado derecho de ec. (44), se encuentra que  es estrictamente negativa por fuera de la esfera
es estrictamente negativa por fuera de la esfera  , dada por:
, dada por:
así, todas las trayectorias de 𝑒 𝑎𝑜 (𝑘) que inicien por fuera de esta esfera convergen hacia su interior, y todas aquellas que inicien dentro de la esfera no la abandonan.
3.2. Ley de control
La Fig. 2 muestra la estructura de control propuesta observador/control. El esquema propuesto está compuesto por:
Un término de estimación/rechazo de perturbaciones 𝜉 𝑟 (𝑘), y otro de estimación de variables de estado, los cuales son suministrados por el observador extendido resonante (ver Proposición 1).
Un término de acción integral para lograr rechazo de perturbaciones cuando 𝜉 𝑟 (𝑘) contenga componentes constantes.
Ganancias de realimentación de variables de estado 𝑘 𝑖 y 𝐾 𝑐 para acomodar la dinámica de lazo cerrado del sistema de control.
De acuerdo a la estructura de control mostrada en la Fig. 2, se construye un sistema en espacio de estados que incluye las variables de estado de la grúa torre y la nueva variable de estado del controlador 𝑤(𝑘); este sistema está dado por:
Donde 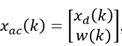 ,
,  ,
,  ,
,  ,
, 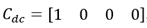 ,
,  ,
,  y
y  . Con base en el sistema aumentado anterior, se propone la siguiente ley de control bajo la filosofía ADR.
. Con base en el sistema aumentado anterior, se propone la siguiente ley de control bajo la filosofía ADR.
Proposición 2 (Ley de control): La ley de control dada por,
donde  es el vector de ganancias de realimentación de estados, k
i
es la ganancia de control integral, y
es el vector de ganancias de realimentación de estados, k
i
es la ganancia de control integral, y  es la posición deseada de la carretilla; acomoda la dinámica del sistema de control para ser dominada por los valores propios de
es la posición deseada de la carretilla; acomoda la dinámica del sistema de control para ser dominada por los valores propios de  con
con  . Con una selección apropiada de
. Con una selección apropiada de  tal que los valores propios de
tal que los valores propios de  estén dentro del círculo unitario, la ley de control obliga el error
estén dentro del círculo unitario, la ley de control obliga el error  a permanecer en una vecindad de cero, rechazando perturbaciones con componentes armónicos de frecuencia ω
r
.
a permanecer en una vecindad de cero, rechazando perturbaciones con componentes armónicos de frecuencia ω
r
.
Demostración 2: La dinámica de lazo cerrado del sistema de control se puede hallar substituyendo ec. (48) en ec. (46), resultando:
Luego de algunas manipulaciones algebraicas, se obtiene
donde  y
y  son errores de estimación de las variables de estado de la grúa-torre y de la función de perturbación, respectivamente. La convergencia de
son errores de estimación de las variables de estado de la grúa-torre y de la función de perturbación, respectivamente. La convergencia de  hacia una vecindad de
hacia una vecindad de  , y de
, y de 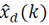 hacia una vecindad de
hacia una vecindad de  , bajo un diseño apropiado del observador (ver Proposición 1 y Demostración 1), establece que los errores de estimación
, bajo un diseño apropiado del observador (ver Proposición 1 y Demostración 1), establece que los errores de estimación  y
y  evolucionan de forma últimamente acotada cerca de una vecindad de cero. Entonces, la dinámica de lazo cerrado del sistema de control es fuertemente dominada por los valores propios de la matriz
evolucionan de forma últimamente acotada cerca de una vecindad de cero. Entonces, la dinámica de lazo cerrado del sistema de control es fuertemente dominada por los valores propios de la matriz  .
.
4. Otros esquemas de control
La estrategia propuesta en la sección 3 se compara con dos esquemas de control que son: un PI vectorial con observador de estados etiquetado aquí como (PI-Vectorial); y un control con acción integral y observador de estado extendido basado en la filosofía ADR, etiquetado aquí como (PI-ADR). El diseño del observador de estado extendido usa un modelo interno convencional de la función de perturbación dado por  , que asume que la función de perturbación
, que asume que la función de perturbación  es constante, como es usado en la mayoría de los casos en ADRC.
es constante, como es usado en la mayoría de los casos en ADRC.
La Tabla 2 muestra los valores propios seleccionados para cada esquema de control/observador, y la Tabla 3 muestra las ganancias obtenidas en cada caso. De aquí en adelante el esquema de control propuesto en la sección 3 es etiquetado como (PI-ADR+R).
5. Análisis de robustez
Las gráficas de Nyquist son utilizadas para analizar y evaluar la robustez de los sistemas de control. La distancia mínima entre la curva de Nyquist y el punto [-1,0j] define el margen de módulo Δ𝑀, e identifica la robustez del sistema de control. Un sistema robusto debe tener un margen de módulo superior o igual a 0.5 [20]. La Fig. 3 detalla el margen de módulo de las curvas de Nyquist de lazo abierto de cada sistema de control: PI-Vectorial, PI-ADR y la propuesta de control etiquetada como PI-ADR+R.

Fuente: Los autores.
Figura 3 Gráficos de Nyquist de los sistemas de control en lazo abierto usando parámetros nominales.
Los sistemas de control presentan altos márgenes de módulo y en consecuencia son considerados robustos. El control PI-Vectorial tiene un margen de módulo de Δ𝑀=0.788, PI-ADR de Δ𝑀=0.792 y la propuesta de control PI-ADR+R de Δ𝑀=0.779. Se puede apreciar que el esquema de control propuesto (PI-ADR+R) muestra un índice de robustez un poco menor que los demás: sólo 1.6% inferior que el margen del PI-ADR, y 1.1% inferior que el margen del PI-vectorial.
6. Resultados experimentales
Para evaluar las técnicas de control propuestas, se realizaron pruebas experimentales sobre una grúa-torre a escala (ver Fig. 4) con el fin de analizar y validar el desempeño y robustez presentado por cada sistema de control. La primera prueba consistió en observar las respuestas de los controladores ante una referencia tipo paso en 𝑥 ∗ para analizar el comportamiento del desplazamiento de la carretilla y de la oscilación de la carga. La segunda prueba analiza las respuestas de los controladores ante rechazo de perturbaciones en la carga. Por último, en una tercera prueba se analizan los sistemas de control cuando se reduce la longitud de la guaya 𝐿 en 25% respecto a su valor nominal. Esta longitud es considerada el parámetro más crítico del modelo de la grúa.
6.1. Caso 1: Referencia tipo paso
En esta prueba se analiza el desempeño y robustez presentados por los sistemas de control ante una entrada tipo paso, cuyo objetivo es posicionar la carretilla en una referencia de 𝑥 ∗ =0.5𝑚 y estabilizar la carga en el punto 𝜃 𝑝 =0. En la Fig. 5, se presenta la respuesta de cada sistema de control para el posicionamiento de la carretilla y de la carga. En esta figura, se puede evidenciar el buen desempeño que presenta la propuesta de control respecto a las otras técnicas. Observe que las oscilaciones de la carga que presentan los controladores PI-ADR y PI-Vectorial en el periodo de tiempo de (5s-10s) están dentro del rango de (±0.5°) y (±1°), respectivamente; mientras que el controlador

Fuente: Los autores.
Figura 5 Respuesta de la posición de la carretilla y ángulo del péndulo ante referencia tipo paso 𝑥 ∗ =0.5 m.
PI-ADR+R atenuó por completo las oscilaciones durante este periodo de tiempo y en adelante. A su vez, en esta figura se puede observar que durante el transitorio (0s-3s) de la prueba, las amplitudes en la oscilación de la carga son mayores en los controladores PI-Vectorial (-5.67°) y PI-ADR (-6.3°), mientras que la propuesta de control PI-ADR+R presentó menores amplitudes de oscilación en la carga (-5.13°).
También observe que durante el periodo de tiempo (5s-10s), los sistemas de control PI-Vectorial y PI-ADR presentan oscilaciones considerables en el desplazamiento de la carretilla. Estas oscilaciones en la carretilla durante dicho periodo de tiempo, son producto de la acción de los sistemas de control para atenuar las oscilaciones en la carga, evidentemente sin beneficios visibles en la reducción de oscilaciones en la carga. En la Fig. 6, se muestra la estimación de la función de perturbación que tuvieron los controladores PI-ADR y PI-ADR+R durante la prueba. En esta figura, se puede apreciar que durante el periodo de tiempo (0s-3s) se presentan señales de alta frecuencia que son producto de las vibraciones y otras dinámicas no modelas presentes durante el transitorio del sistema. En la Fig. 7, se presentan las señales de control de cada esquema de control durante la prueba.

Fuente: Los autores.
Figura 6 Estimación de la función de perturbación entregada por los esquemas de control PI-ADR y PI-ADR+R durante la prueba de referencia tipo paso en la posición de la carretilla.
6.2. Caso 2: Perturbaciones en la carga
Esta prueba consistió en posicionar y sujetar la carga en el punto 𝜃 𝑝 =10°. Posteriormente, al ser liberada la carga, esta desarrolla una trayectoria pendular no controlada, que la obliga a pasar por el punto 𝜃 𝑝 =0°. En este punto, los esquemas de control son activados con el objetivo de rechazar las perturbaciones que afectan el sistema y a su vez atenuar las oscilaciones en la carga con 𝑥 ∗ =0. De esta forma, esta prueba busca evaluar y analizar el desempeño y robustez de los sistemas control ante el rechazo de perturbaciones, estabilizando la carga en el punto 𝜃 𝑝 =0°. Esta prueba solo incluye información experimental desde el momento en que se activan los esquemas de control.
En la Fig. 8, se presenta la respuesta de cada sistema de control durante la estabilización de la carga. En esta figura, se puede apreciar cómo el controlador PI-ADR+R atenúa de mejor forma las oscilaciones en la carga en comparación con los otros controladores. Observe que la carga en el periodo de tiempo (5s-10s) presenta menores amplitudes de oscilación en comparación a los otros sistemas de control, mostrando así un mejor desempeño para atenuar las oscilaciones en la carga. En la Fig. 9, se presenta la estimación de la perturbación obtenida por los sistemas de control PI-ADR y PI-ADR+R durante la prueba. En la Fig. 10, se presentan las señales de control de cada esquema de control. En esa figura, se puede apreciar que el controlador PI-ADR+R presenta menores valores pico en la señal de control aplicada al actuador.

Fuente: Los autores.
Figura 8 Posición de la carretilla y ángulo del péndulo en la prueba de estabilización/perturbaciones en la carga. Considerando 𝑡=0𝑠, el momento de activación de los esquemas de control.

Fuente: Los autores.
Figura 9 Estimación de la función de perturbación de los esquemas de control PI-ADR y PI-ADR+R durante el caso 2.
6.3. Caso 3: Variación en la longitud de la cuerda
Considerando una variación de −25% en la longitud nominal de la guaya (ver Tabla 1), se realiza una prueba ante referencia tipo paso para posicionar la carga y la carretilla con una referencia de 𝑥 ∗ =0.5𝑚. Esta prueba evalúa el desempeño y robustez del esquema de control propuesto ante variación de parámetros en el sistema.
La Fig. 11 muestra los resultados obtenidos en esta prueba indicando las propiedades de robustez y desempeño del esquema de control propuesto (PI-ADR+R). Observe que el esquema de control PI-Vectorial resulta inestable aun cuando su margen de módulo es 1.6% superior. Estos resultados experimentales dan la realidad de la robustez de los esquemas de control basados en la filosofía del rechazo activo de perturbaciones, donde se estiman y rechazan en línea las perturbaciones que afectan al sistema incluyendo términos no lineales como fricciones estáticas/coulomb.

Fuente: Los autores.
Figura 11 Respuesta de posición de la carretilla y oscilación de la carga en la prueba de posicionamiento de la carretilla 𝑥 ∗ =0.5m teniendo en cuenta una variación en la cuerda de −25%.
Adicionalmente, la Fig. 11 muestra que el desempeño del esquema PI-ADR se ve afectado (dada la incertidumbre del sistema), mostrando gran cantidad de variaciones en el ángulo de oscilación de la carga y en el posicionamiento de la carretilla. Esto muestra que el aniquilador propuesto en ec. (29) proporciona mejores resultados que el modelo interno convencional usado en esquemas clásicos ADRC como el mostrado en la sección 4.
6.4. Análisis de desempeño
Para obtener una medida del desempeño de los esquemas de control, se calculó la energía de las señales más relevantes de cada sistema de control como un índice de desempeño en cada experimento. Consideramos la energía del ángulo de oscilación de la carga como  y la energía de la señal de control como
y la energía de la señal de control como  .
.
La Tabla 4 muestra el resumen de los índices de desempeño encontrados. Para facilitar el análisis de la tabla, los índices de desempeño se ponderan en términos porcentuales relativos a los obtenidos por el esquema de control propuesto (PI-ADR+R). Así entonces, se puede notar que en los tres casos experimentales, la estrategia de control propuesta tiene mejor desempeño en términos de atenuación de oscilaciones en la carga y además se logra usando menor cantidad de energía de control.
7. Conclusiones
En este artículo, se propuso un esquema de control en tiempo discreto bajo el enfoque del rechazo activo de perturbaciones para abordar el problema de oscilaciones presentes en la carga de grúas-torre. La propuesta de control se diseñó con un observador de estado extendido que incluyó un elemento resonante que dio la habilidad de mejorar las estimaciones de las variables de estado y de la perturbación cuando se presentan oscilaciones en la carga.
El esquema de control propuesto evidenció experimentalmente mejor desempeño en comparación con otros controladores (PI-Vectorial y PI-ADR), mostrando menores amplitudes de oscilación en la carga durante la respuesta transitoria y estacionaria de cada prueba. Este desempeño se evidenció inclusive, cuando los esquemas de control estaban sometidos a incertidumbres paramétricas y perturbaciones externas.
Por otra parte, se encontró la robustez de cada sistema de control usando la gráfica de Nyquist obteniendo un margen de módulo superior a 0.77 en todos los esquemas de control evaluados. No obstante, en comparación con los otros esquemas de control, los resultados experimentales mostraron que la propuesta de control conserva un desempeño adecuado en la atenuación de las oscilaciones en la carga, pese a una variación de −25% en la longitud nominal de la cuerda 𝐿.