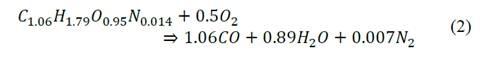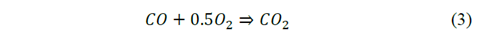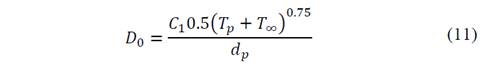1. Introduction

The use of sugarcane bagasse as a fuel for steam generation is widely used throughout South America because, besides the production of sugar, the sugarcane juices are converted into ethanol. In countries as Colombia, ethanol is mixed with regular gasoline up to 20%, while in Brazil, ethanol is sold as fuel and most vehicles can run indifferently on ethanol or gasoline. Brazil is by far the largest producer of sugarcane in the world, producing more than 730 million tons in 2014 [¹] and the second largest producer of ethanol in the world [²].

Steam generation throughout the world has traditionally ran on pulverized coal, and the modeling of this combustion can be considered a mature technology. It is common in countries as Colombia that industrial boilers shift from pulverized coal to pulverized bagasse due to the increase availability and lower price of this biofuel. However, since most of the work on combustion modeling in boilers has been done on coal, it is still difficult to obtain in the literature certain parameters necessary to properly model the bagasse combustion.

The major difference between coal and bagasse is probably the water content. Since the moisture content in coal is usually below 10%, in the bagasse can be up to 56% and, in most cases, is not economically beneficial to dry it out, and it is used as received. This causes a significant load of water in the flue gases and a reduction of the adiabatic flame temperature [³]. Kaewpradap, Yoksenakul & Jugjai [³] assure that a bagasse with moisture content over 56% leads to unstable combustion. According to Shrivastav & Hussain [⁴] each 1% reduction in the bagasse moisture increases 0.5% the efficiency of the boiler.

Another major difference between coal and bagasse is the volatile content, biomass always has greater volatiles content, even when compared to low-rank coals [⁵]. The ratio of volatile matter to fixed carbon is typically greater than 4.0 for biomass and lower than 1.0 for coal [⁶]. This makes devolatilization models and volatile composition of significant importance in the modeling of bagasse combustion. Devolatilization is usually modeled as a first order single rate Arrhenius equation such as presented by Ferreira et al. [⁷], Zahirovic, Scharler & Obernberger [⁸], Jin et al. [⁹], Aboyade et al. [¹⁰] and Sanchez & Mendieta [¹¹]. However, according to Smith [¹²] this single rate models cannot accurately represent the devolatilization rate. Centeno-González et al. [⁵] presented a two-stage devolatilization model and it is used in this work. Molecular weight of volatiles has been suggested in the range of 20 g/mol [¹³] up to 30 g/mol [⁵].

Bagasse particles are in most cases, modeled in a Eulerian-Lagrangian approach, also known as discrete phase [⁵,⁶,⁸,⁹,¹²,¹³]. In this model, the particles are tracked in a continuous phase to which exchange mass and heat. It is recommended that the volume fraction of particles to be below 10% [¹⁴], however in grate boilers, the bagasse particles piled up above the grate and unfulfilled that condition. In this particular case, the particles do not behave as a discrete phase and a full Eulerian approach would be more appropriate (also known as granular phase). However, the use of granular phase represents a huge increase in computational effort since governing equations have to be solve for both phases (continuous and granular), while in discrete phase, governing equations are solved only for the continuous phase and particles are tracked every certain number of iterations. The size of an industrial boiler makes almost prohibitive the use of a granular phase for the fuel particles due to the computational effort, one of the few simulations presented in the literature in this manner is from Ferreira et al. [⁷]. Nevertheless, the issue of the pilling of particles above the grate can be managed, as it will be presented further in this work.

The simulation of an industrial boiler by CFD commercial software ANSYS FLUENT is presented in this work. Due to the size of the boiler, it was divided into three models, the primary air circuit, the secondary air circuit and the furnace. The primary and secondary air are connected to the furnace by profiles of velocity, temperature, turbulent kinetic energy and dissipation rate. A baseline simulation was performed trying to reproduce the main operational parameters, once the results of the simulation reproduced the experimental data with a satisfactory agreement; an optimization of the boiler performance was accomplished. Primary and secondary air inlets were modified and the results of the optimization simulation showed a significant improvement of the operational parameters when compared to the baseline simulation.

2. Flow geometries

The geometry of the primary and secondary air circuits and furnace are presented in Figs. 1-3. Air preheaters in primary and secondary air circuits and superheater in furnace correspond to plain tube banks and are not physically modeled, yet they are modeled as a porous zone. In order to account for the pressure loss through the tube bank, viscous resistance ( D 𝐣 ) and inertial resistance ( 𝑪 𝒋 ) have to be properly estimated [¹⁵] and included as a source term ( 𝑺 𝒊 ) in the momentum equation (eq. 1) where 𝒗 𝒋 corresponds to velocity in j direction. The pressure loss in a direction parallel to the tubes can be negligible, and the viscous and inertial resistance can be set to zero. In the other two directions, the tube bank can be treated as a packed bed and the parameters can be estimated with Ergun´s correlation [¹⁶] and are presented on Table 1.

Source: The authors.

Figure 1 Geometry of the primary air circuit.  

Source: The authors.

Figure 2 Geometry of the secondary air circuit.  

Figure 3 Geometry of the furnace.  

Source: The authors.

Table 1 Inertial and viscous resistance for primary and secondary preheater, superheater and the grate. 

Source: The authors.

The grate has 25800 orifices of 9.5mm diameter. Thus the physical simulation of the grate would cause an unmanageable mesh size. Nevertheless, Gan & Riffat [¹⁷] assure that perforated plates can be properly modeled by setting viscous resistance to zero and adjusting inertial resistance to provide the proper pressure drop and flow direction. Inertial resistance values found under these stipulations are shown in Table 1.

3. Physical models

Primary and secondary air circuits were simulated by the solution of continuity, momentum and energy equations with the standard k-epsilon turbulence model. In the furnace; continuity, momentum and energy equations with the standard k-epsilon turbulence model were also solved for the continuous phase (gases), besides the discrete ordinates model for radiation and the eddy dissipation model for the species reactions as recommended by Tabet & Gökalp [¹⁷]. Particles are modeled as a discrete phase. Detailed description of these equations can be found on reference [¹⁴].

3.1. Volatile combustion modeling

Two components of the bagasse participate in the combustion, the volatiles and the char. The combustion of volatiles is modeled from the creation of a representative molecule with an atomic composition estimated from the elemental analysis of the bagasse (Table 2) and an estimated molecular weight (30 g/mol). Also, the standard state enthalpy of this molecule was estimated from the higher calorific value (HCV) of the bagasse. (8118498 J/kg). The two-step stoichiometry is presented in eq. (2) - (3).

Table 2 Elemental and proximate analysis of the bagasse in wet basis.  

Source: The authors.

In the eddy dissipation model [¹⁸] the net rate of production of the specie i due to reaction r ( 𝑅 𝑖,𝑟 ) is given by the smaller value calculated by eq. (4) or (5). Parameters A and B are known as Magnussen constants, 𝜈 𝑖,𝑟 ′ corresponds to the stoichiometric coefficient, 𝑀 𝑤,𝑖 to the molecular weight, 𝜀 𝜅 to the ratio of turbulent kinetic energy/dissipation rate and 𝑌 𝑅 to the mass fraction.

The values of A and B default by FLUENT are 4.0 and 0.5 respectively. Those values were found empirically for the combustion of gases and produced unrealistic high flame temperatures and low CO concentration in the simulations. At the best of our knowledge, the only work in the literature dedicated to estimate the Magnussen constants for the combustion of biomass is the one presented by Scharler, Fleckl & Obernberger [¹⁹]. They recommend values of 0.6 and 0.5 for Magnussen constants A and B respectively. With those values, the simulations calculated a CO concentration and flame temperature of satisfactory agreement to the experimental values.

3.2. Particle modeling

As already mentioned, bagasse particles are modeled as a discrete phase. These particles pass through a process of heating, moisture evaporation, volatile evaporation, char combustion and ashes heating/cooling.

As the moisture content in the bagasse is high, also a high vaporization rate is expected. In this case, a convection diffusion method for the mass transfer from the particle to the continuous phase is recommended [¹⁴]. In Eq. (6), taken from the work of Miller [²⁰] and Sazhin [²¹]; 𝑚 𝑝 corresponds to the mass of the particle, 𝑘 𝑐 to the mass transfer coefficient, 𝐴 𝑝 to the particle surface area, 𝜌 𝑐 to the gas density and 𝐵 𝑚 to the Spalding mass number.

Volatilization rate is an important feature since 95% of the combusting constituents of the bagasse are volatiles. The devolatilization model used in this work is from Centeno-González et al. [⁵] and is presented on eq. (7) and (8). This model was programmed in C language as a UDF with the parameters presented on Table 3, where 𝛼 corresponds to the conversion fraction, K to the pre-exponential factor, E 𝑎 to the activation energy, ?? 𝑝 to the particle temperature and 𝑅 to the universal gas constant.

Table 3 Parameters for the devolatilization model. 

Source: [⁵]

Once the particle passed through evaporation and volatilization, the char fraction is left to be consumed by the combustion process with the stoichiometry presented in eq. (9). Based on Baum and Street [²²] and Field [²³] models, char combustion rate is calculated with Eq. (10) with diffusion rate coefficient ( 𝐷 0 ) of Eq. (11) and kinetic rate (𝜓) of Eq. (12).

In eq. (10)-(12), the mass diffusion limited rate ( 𝐶 1 ), the kinetic limited pre-exponential factor ( 𝐶 2 ) and the kinetic limited activation energy ( 𝐸 𝐶 ) are from Luo & Stanmore [²⁴]. Those parameters are on Table 4. Also, in eq. (10)-(12) 𝑚 𝑝 corresponds to the mass of the particle, 𝐴 𝑝 to the surface area, 𝑃 𝑜𝑥 to the partial pressure of oxidant species, 𝑇 ∞ to the ambient temperature and E 𝑐 to the activation energy of the char combustion reaction.

Table 4 Parameters for the char combustion model. 

Source: [²⁴]

Default swelling coefficient in FLUENT is 1.4, which is appropriate for coal particles that expand during devolatilization. However, bagasse particles behave the opposite way, according to Li et al. [²⁵] as they tend to shrink and a swelling coefficient of 0.7 would be more appropriate.

4. Boundary conditions

The main operational parameters and boundary conditions for the simulation of the boiler are presented in Table 5. Four injections of bagasse particles were performed as function of a particle size distribution that was experimentally measured in a gradation test and can be seen in Table 6.

Table 5 Main operational parameters for the boiler. 

Source: The authors.

Table 6 Diameter and mass flow of every injection of bagasse particles. 

Source: The authors.

Profiles of velocity, temperature, turbulent kinetic energy and dissipation rate calculated in the simulation of the primary and secondary air circuits were used in the simulation of the furnace as boundary conditions for the grate and the secondary air inlets. The location of the grate and the secondary air inlets can be seen on Fig. 3.

It is seen on the operation of the boiler how the bagasse particles tend to pile up above the grate, in order to emulate this behavior in the discrete phase model, it is necessary to trap the particles in the grate. In the rest of the boundaries, particles are reflected except in the outlet, where they scape.

5. Results and analysis

Fig. 4 presents the velocity profile on the grate calculated by the simulation of the primary air circuit. It is notorious the higher velocity in the upper part, which corresponds to the wall where the bagasse feeders are located (Fig. 3). This unbalanced distribution of flow provides an opportunity of improvement that will be exposed further in this paper.

Source: The authors.

Figure 4 Velocity profile on the grate (m/s). 

Fig. 5 presents the contours of velocity on each one of the six levels of secondary air inlets in the furnace, being level one, the closer to the bottom and level six, the farthest (see Fig. 7). These contours were obtained in the simulation of the furnace using the velocity profiles calculated in the simulation of the secondary air circuit. It is observed how the highest velocities are found nearby the walls and the lowest by the center. These contours also show a not properly distributed flow inside the furnace that can be improved by a rearrangement of the air nozzle angles.

Source: The authors.

Figure 5 Contours of velocity magnitude (m/s) found in the simulation of the furnace. 

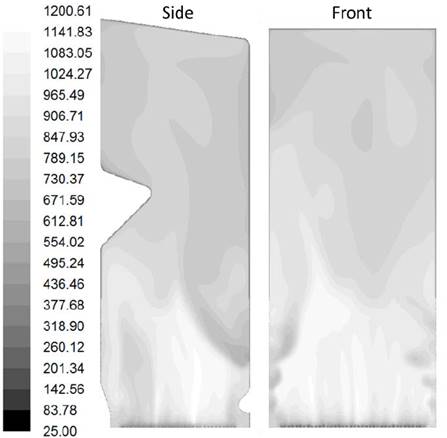
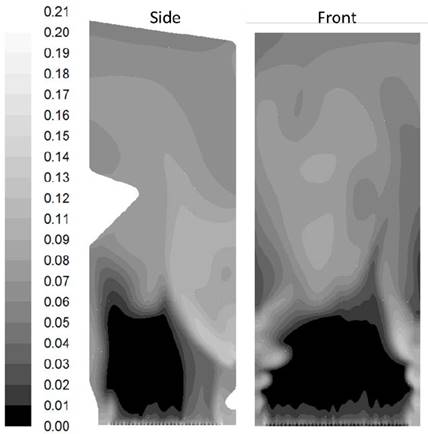
Contours of temperature and molar fraction of O₂ found in the simulation of the furnace are presented in Fig. 6. and 8. The unbalanced distribution of flow on the grate generates higher temperature at the bottom towards the bagasse feeder’s wall as seen on the side contour of Fig. 6. Similarly, the side contour of Fig. 8 shows a reduction of the O₂ fraction towards the opposite wall of the bagasse feeders also caused by the unbalanced distribution of flow on the grate. Location of the planes side, front, level one and level six on the furnace can be seen in Fig. 7.

Source: The authors.

Figure 6 Contours of temperature (°C) found in the simulation of the furnace. 

Source: The authors.

Figure 7 Location of the planes side, front, level one and level six. 

Source: The authors.

Figure 8 Contours molar fraction of O₂ found in the simulation of the furnace. 

A comparison of the available experimental data with the results of the simulation of the furnace is presented on Table 7. Temperatures and molar fraction of O₂ and CO₂ show a satisfactory agreement with a percentage of deviation below 5%. However, the concentration of CO is almost 20% deviated from the measured value. Since the CO is an intermediate species in the combustion reaction, it is probably the most difficult to predict. Besides, the concentration of CO is highly dependent on the values of the Magnussen constants (eq. 4-5). A simulation was performed with default FLUENT values (A=4.0, B=0.5) and it calculated a temperature in the lower furnace of 1342°C and a concentration of CO of 0.1568 ppm in the outlet. Those values show a significant difference with the measured data presented in Table 7 and it reveals the strong dependence of the flame temperature and formation of CO with the Magnussen constants.

Table 7 Comparison of measured data with the results of the simulation. 

Source: The authors.

Table 8 presents a summary of the behavior of the bagasse particles after evaporation, devolatilization and char combustion. Results show that the grate traps most of the biggest particles while the whole of the smallest leave the furnace. The residence time is, evidently, greater in the particles that leave the furnace. The sum of the particles trapped by the grate and leaving the furnace is 0.6072 kg/s and the load of ashes in the bagasse is 0.5948 kg/s (see Table 2) which means that 0.0124 kg/s was left unburned. The flow of particles leaving the furnace (0.33594 kg/s) should correspond to the particulate matter in the flue gases. Unfortunately, there is not experimental measurement of this parameter to confirm the validity of this value.

Table 8 Summary of the behavior of the bagasse particles. 

Source: The authors.

6. Optimization

The first improvement sought to balance the air flow distribution on the grate. For that purpose, a series of deflectors were located under the grate to evenly distribute the streamlines and can be seen on Fig. 9. The contours of velocity magnitude on the grate found in the simulation of the primary air circuit with the mentioned modifications is shown in Fig. 10. It is seen, a more balanced distribution of the flow.

Source: The authors.

Figure 9 Deflectors under the grate in the primary air circuit. 

Source: The authors.

Figure 10 Velocity profile on the grate (m/s) after optimization. 

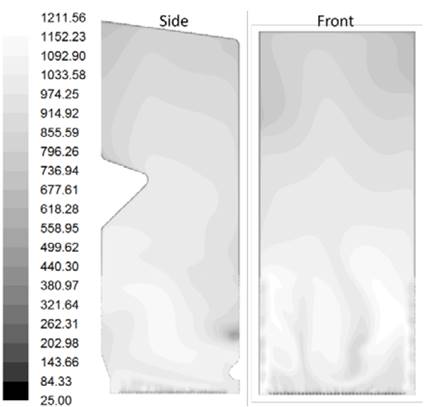
The entry angle to the furnace of the secondary air nozzles was modified to create two vortexes that enhanced the mixing of air and volatiles and provided a more balanced distribution of the flow inside the furnace (Fig. 11). As result of this modification, the simulation showed a significant reduction of the CO concentration in the outlet, which represented an increase of 1.3% in the combustion efficiency as seen on Table 9. The combustion efficiency was calculated with eq. (13) where 𝑋 𝐶𝑂 2 and 𝑋 𝐶𝑂 correspond to the molar fraction of CO₂ and CO respectively. In Table 9 can also be seen an increase in the CO₂ concentration as result of the reduction of CO formation. Contours of temperature found in the simulation of the furnace, after optimization of the air flow on the grate and the entry angle of the secondary air nozzles, are presented in Fig. 12. This figure shows a more balanced distribution of the temperature in the lower furnace.

Table 9 Comparison of the baseline and the optimized simulation. 

Source: The authors.

Source: The authors.

Figure 11 Contours of velocity magnitude (m/s) found in the simulation of the furnace after optimization. 

Source: The authors.

Figure 12 Contours of temperature (°C) found in the simulation of the furnace after optimization. 

Table 10 presents the behavior of the bagasse particles after evaporation, devolatilization and char combustion in the baseline and the optimized simulation. Here, it can be seen an important increase in the mass of particles trapped by the grate and a reduction of the particles leaving the furnace which indicates a reduction of the particulate matter in the flue gases.

Table 10 Behavior of the bagasse particles in the baseline and the optimized simulation. 

Source: The authors.

7. Conclusions

The simulation of the combustion of bagasse is a complicated task since it involves a series of physical processes such as heating, vaporization, devolatilization, char combustion and ash heating/cooling. The literature is still scarce on studies regarding devolatilization and char combustion of bagasse particles. Most studies model devolatilization with a first order single rate Arrhenius equation, yet researchers [¹²] have pointed out that single rate models cannot accurately represent devolatilization. At the best of our knowledge, the only set of kinetic parameters available in the literature to simulate the char combustion of sugarcane bagasse are from Luo & Stanmore [²⁴]. In their work, a single sample of bagasse is analyzed; therefore, it is uncertain the effect of the composition of the bagasse in the kinetic parameters for char combustion.

At the best of our knowledge, the effect of the Magnussen constants for the eddy dissipation model in the combustion of biomass has been analyzed only by Scharler, Fleckl & Obernberger [¹⁹]. The default values of these constants provided by FLUENT calculated unrealistic high temperatures (1342°C) and extremely low CO formation (0.1568 ppm). With the values proposed by Scharler, Fleckl & Obernberger the simulation calculated a temperature in the low furnace with a 4.95% of deviation from the measured value and a CO concentration in the outlet with a 19.46% of deviation. These results indicate that there is a strong dependence of the flame temperature and the formation of CO with the Magnussen constants. However, Scharler, Fleckl & Obernberger studied only the effect of the A constant in the formation of CO while the B constant was left fixed in a value of 0.5. This means that only the effect of the A Magnussen constant has been studied in the combustion of biomass and there is still, uncertainty regarding the effect of the B constant in this matter.

The baseline CFD simulation provided an insight of the performance of the boiler and permitted the development of a series of modifications that optimized that performance. The results of the simulations after optimization of the boiler showed an increase of 1.3% in the combustion efficiency and a reduction of 53% in the particulate matter in the flue gases.