1. Introduction
The technological and industrial development, the increase of the industrial production and populations’ growth, increases the industrial and domestic liquids residues in volume, load, concentration and variety. Discharging this wastewater on the receiving bodies, also increases the degree of contamination and leads to very harmful effects on the different lifeforms present in these currents; breaking the biological balance, altering each one of the components on the biodynamic cycle, reaching to the extreme of causing illness and death. These actions have induced researchers to develop different types and systems of treatment, tending to reduce impacts and effects.
At the urban level, for example, one of the main sources of organic pollution are those produced by liquid discharges from municipal slaughterhouses, which report very high concentrations of Biochemical Oxygen Demand (BOD5), fats, solids and fecal coliforms, with great impact on sanitary sewerage networks, which is more noticeable in medium and small populations, a situation that forces to perform treatments before discharges. In general terms, chemical treatments offer high efficiencies in the removal of contaminants, but at very high construction and operating costs of wastewater treatment plants WWTP. This fact has led to the emergence of biological treatments, through systems that have been well received because they are relatively easy to build, economical and efficient (> 80% COD).
The models for the design of sewage treatment systems with adhered biofilm are used to estimate the yields in the removal of Organic Matter (OM) contained in the wastewater. According to [1], among the most important are: 1) the rotating biological contactors [2-5]; 2) trickling filters [6,-15]; 3) those of activated biological carbon [16,17], 4) biofilters [18]; 5) submerged filters [19]; 6) fluidized beds [20]; 7) packed beds [21] and 8) anoxic and anaerobic biofilm systems [22,13].
According to Young J.C. and McCarty [23], the anaerobic filter has advantages compared to other biological treatments including: It is suitable and ideal for the treatment of waste; does not require recirculating effluents or solids; the biological solids remain in the filter and are not lost with the effluent and the accumulation of high concentrations of active solids in the filter allow the treatment of diluted residues even at nominal temperatures; heating is not necessary as in most other anaerobic processes to maintain a high efficiency of treatment, produce very low volumes of sludge with free effluents of suspended solids; and the waste of mud, in some cases, is practically non-existent. These facts contrast with the aerobic biological processes that produce large volumes of sludge, containing more than half of the BOD5’s original waste and requiring treatment before dumping.
In this study an innovative variant to the anaerobic upflow filters now separated in two phases DI-FAFS and in three phases TRI-FAFS (of acronyms in Spanish) is presented, with a plastic support medium where microorganisms adhere with the purpose of formulating the mathematic models to predetermine the performance in removing the OM expressed as COD, as a result of the equations’ adaptation formulated for trickling filters (the most studied to proposal for mathematical formulations) and the equations anaerobic biofilters; using as experimental factors: the Volumetric Organic Load (VOC); the temperature (T) and depth ratio between the first D1/D2 and second phase and the second and third phase D2/D3.
2. Materials and methods
This research was developed in the water laboratory of the Water, Air and Soil Environmental Research Group - GIAAS - Faculty of Engineering and Architecture of the University of Pamplona - Colombia, who financed the research, directed by the Center for Hydrological and Environmental Research - CIHAM - with the assistance of the Institute of Mathematics and Applied Calculus (IMYCA) both from Venezuela.
2.1. Experimental design
It is factorial (33), with three independent variables: VOC; T and depth ratio D1/D2 and D2/D3, each variable with three quantitative levels to determine the effects, in three levels of response and nine treatments.
2.2. Methods
The following activities and sequential procedures were carried out:
Characterization of leachates: Six samples were taken at the Los Guayabales landfill in Cúcuta - Colombia. The Table 1 illustrates the parameters analyzed.
Table 1 Leachates’ Physical-chemical parameters from the Los Guayabales landfill - Cúcuta- Colombia.
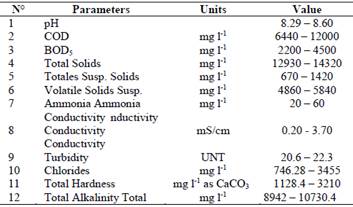
Source: the authors
Determination of Specific Methanogenic Activity (SMA): Methodology proposed by Field, J. [24]. Sludge’s experimental conditions: Container volume: 1.0 l, Concentrations of: Sludges with 1.36 g SSV/l; Volatile Fatty Acids VFA: 4 g COD/l; T: 27°C; pH: 7.1; system: without agitation. A first and second feed was applied with VFA at 27°C, determining four indices: 1) R or production rate of CH4; 2) the SMA: 3) the Observed Activity Increase Index (OAII); 4) the Expected Theoretical Index of Increase Activity (ETII) to three slimes from Colombian WWTPs and a fourth pig manure. According to Field J. [24] if OAII < 2 * ETII then the response of microorganisms to the substrate is by growth instead of adaptation, and vice versa; reporting pig manure as the largest SMA on the first sludge feed.
Feeding system: Integrated by a storage tank for the crudow leachates, thermostated by pallets driven by a motor-reducer of vertical axis of timed operation, from where they are fed by means of nine dosing pumps and with flow rates: 3.5 - 4.0 ml/min DI-FAFS or TRI-FAFS, through plastic connections Ø = 1/4" between the storage tank and the nine reactors and the biogas separators.
Reactors’s design and construction: As a pre-treatment, two grease traps were designed and built in parallel, each with a length of L = 0.16 m, width of B = 0.04 m, depth H = 0.08 m, volume V = 0.512 l, with Hydraulic Retention Time (HRT) = 0.43 h; the effluents converge in a primary settler of L = 0.32 m, B = 0.16 m, H = 0.08 m, V = 4.096 l and HRT = 1.73 h and total HRT of pretreatment of 2.16 h. Each up flow anerobic filters reactor FAFA (of acronyms in Spanish) was separated into two and three sequential sub-phases in the flow direction, DI-FAFS and TRI-FAFS. In the DI-FAFS; the Phase with a volume V1 and the Phase 2 a volume V2; the total reactor volume being Vtotal = V1+V2. In the TRI-FAFS: sequential phases in the flow direction: Phase 1 + Phases 2 + Phase 3; whose volumes in the direction of flow are V1, V2 and V3 and the Vtotal = V1+V2+V3.
From the DI-FAFS and TRI-FAFS reactors, three series were designed and constructed, each series with three DI-FAFS and TRI-FAFS reactors for a total of nine plastic body reactors in each assembly. In the DI-FAFS reactor, the heights in each series vary according to the percentage ratio Phase1/Phase2: 80%/20%; 50%/50% and 20%/80% of total depth D. In the TRI-FAFS reactor, Phases 1 and 2 maintained the volumetric division ratios considered in the DI-FAFS: 20/80%; 50/50% and 20/80%. TRI-FAFS’ phases 1, 2 and 3 have variable percentage heights as follows: Phase1/Phase2/Phase3 of: 4/16/80%; 10/10/80% and 16/4/80% of total reactor volume. In both cases, the sum of the depths of phases is equal to the total height of 1.20 m. and the total useful volume in each reactor of 3.80 l. The entrance duct Φ = 1/4" is located at the bottom; where the pre-treated leachate enters ascendingly. The HRT in each DI-FAFS and TRI-FAFS reactor is 18 ± 0.5 h; 16 ± 0.5 h; respectively. Through a duct of Φ = 1/4" the liquid-gas mixture is discharged to a separator where the biogas flows through the dome and the effluent laterally.
Support medium: The body of DI-FAFS and TRI-FAFS reactors in each phase was packed with pieces of PVC pipe of cylindrical shape of Ø = 1/2", L = 0.01 m (+/- 0.002) with area specific of 476.35 m2/m3, material that does not generate alterations to the substrate, nor to the adhered biomass, allowing the biotreatment of substrate without alterations and with high organic loads.
Inoculation: each DI-FAFS and TRI-FAFS’ sub-phase was inoculated with pig manure, adding a volume of sludge equivalent to 30% volume of each sub-phase.
Initial formation of the adhered biofilm to the support medium: it was achieved by recirculating all the DI-FAFS and TRI-FAFS for seven days only municipal waste water between 250 - 800 mg COD/l.
Adaptation and acclimatization: it was later achieved by supplying to the already formed biofilm, a volumetric mixture of Domestic Residual Water DRW and leachtates, which reduced the volume of DRWs by 5% every 24 hours and increased the volume of diluted leachates with concentrations in the same percentage predefined constants for each of the three series of DI-FAFS and TRI-FAFS as follows: Series1low: 1700 mg/l; Series2media: 2600 mg/l and Series3high: 3500 mg COD/l. Daily at 20°C, 36 l of mixed water was prepared until recirculated in all the reactors only leachtates.
Start-up and operation of DI-FAFS and TRI-FAFS: The treatment of leachates with T at 20ºC was started constant in all the series and with variable VOCs in each one of them; Series1 VOClow = 2.25, Series2 VOCmedium= 3.45 and Series3 VOChigh = 4.64 kgCOD/m3d, periodically performing COD measurements of input and output, which allowed monitoring the efficiency of each reactor during the operation time, until stable conditions were obtained for each load at 20°C, then the mean T was increased to 27°C and finally to high T of 34°C, always monitoring the concentrations of effluent and affluent COD in all the DI-FAFS and TRI-FAFS, during a continuous time of hundred days; in each case.
DI-FAFS and TRI-FAFS reactors evaluation: This was done by determining the efficiency of each reactor under steady-state conditions with variability of ± 5%.
DI-FAFS and TRI-FAFS mathematical model development: Finally, a deep bibliographical revision was made and according to the results obtained in each of the research’s phases and the theoretical-empirical formulation of a series of models was carried out. Mathematics supported on variables such as VOC, number of phases, depth, temperatures and efficiency in the removal of OM and after a statistical analysis and a mathematical modeling, it is possible to determine and present the best statistical adjustment models that allow predict the biodegradation of OM in the leachates from landfills.
3. Theoretical formulation
As an innovative variant the FAFA is presented, separated into two phases DI-FAFS and three phases TRI-FAFS; with plastic support to which the microorganisms adhere and the residual water flows through the medium. The OM present in the wastewater is degraded by the action of microorganisms adhered to the medium that suffer variations mainly due to the following factors: 1) filter’s depth D, 2) changes in the VOC measured in terms of BOD5 or COD, 3) the hydraulic load, 4) pH and 5) T; among others, factors must be taken into account to predict the performance of DI-FAFS and TRI-FAFS reactors.
Several researchers have proposed equations to describe the performance in the elimination of OM adhered to the biofilm systems; among those who have had the most theoretical formulations are the trickling filters; whose mathematical developments have been proposed by: [6,8,9,11,25-30].
In this article we analyze the formulation of a hybrid model that describes elimination of OM performance for the DI-FAFS and TRI-FAFS reactors; combining a conceptual and empirical approach based on the mass balance and the derivation of components’ parametric equations included in the balance from experimental data, respectively.
The mass balance corresponding to OM contained in the volume of liquid within an FAFA is as indicated in Eq. 1:
Where ((∂S ̅)/(∂t)dV): substrate accumulation rate over time within the system limits, Q: volumetric flow rate, m3/day, QS: amount of substrate entering the element of volume, Q (S + (∂S/∂Z)*dZ) amount of substrate leaving the volume element, rs: OM flow rate into the biological layer’s interior, dVrs: substrate flow from the elementary volume to the biological film’s interior, w: section’s width, m, Z: filter’s depth, m. Assuming stationary conditions ((∂ S :)/(∂t) = 0), Eq. 1 can be simplified to reach Eq. 2:
Atkinson [30] adapted the Monod Equation [31] generated under experimental conditions, according to which it was demonstrated that if the substrate or nutrients for the growth of microorganisms are present in limited quantities; once the substrate has been depleted the growth will stop. The model adapted for trickling filters that describes the flow rate of M.O. towards the biological film corresponds to Eq. 3:
Where f: proportionality factor; h: biological layer’s thickness, m; k0: maximum reaction rate, 1/d,  : average concentration of substrate (BOD5 or COD) in mg/l, Km: constant of half speed, substrate concentration at half of the maximum specific growth rate, mg/1. Substituting Eq. 3 in Eq. 2; where dV: is the liquid volume difference of biological and liquid layer’s thickness unit within the system’s limits expressed as dV= wdZ; assuming that the constant’s value of Km is small in relation to the substrate, we obtain:
: average concentration of substrate (BOD5 or COD) in mg/l, Km: constant of half speed, substrate concentration at half of the maximum specific growth rate, mg/1. Substituting Eq. 3 in Eq. 2; where dV: is the liquid volume difference of biological and liquid layer’s thickness unit within the system’s limits expressed as dV= wdZ; assuming that the constant’s value of Km is small in relation to the substrate, we obtain:
Integrating between the Se and Si limits; 0 and D, we have Eq. 5:
Where: Si and Se are the concentrations of OM (COD) in the wastewater’s mixed effluent to be treated and in the affluent respectively, mg/l. Eq. 6 is equivalent to the kinetic reaction of a substrate such as BOD5 formulated according to a first-order derivative [32]:
Where Lt is the first phase’s amount of BOD remaining in the water at time t (d), and k is the reaction constant (1/d). The integration of Eq. 6 between Se and Si, t = 0 and t; results in Eq 7.
Combining Eq. 5 with Eq. 7, the parameter k can be explained in terms of f, h and k0 (Eq. 8); as well as t is equal to wDQ-1 (Eq. 9); transforming a mathematical expression dependent on kinetics by a geometric one associated with filter’s depth (D) as it has been proposed [33].
Eq. 8 and 9 are modified to incorporate substrate’s concentration in the Si tributary and express wastewater flow (Q) in VOC’s terms as it has been proposed by [13,34,35] considered in this study as a variable that affects the description of general kinetics of DI-FAFS and TRI-FAFS reactors, resulting in Eq. 10 and 11:
Being:
Since the mid-twentieth century, equations for the description of trickling filters performances of one or several phases consisting mainly of natural material such as stone and a orientation of descendent flow have been predominantly empirical expressions instead of theoretical; the latter have proved difficult to adjust to the reality of operation for this type of filters with different recirculation ratios; what has been attributed to the stone material’s irregularity [36-38]. Other researchers have found that conceptual models based on mass balances on microorganisms tend to explain the removal of organic and inorganic material that takes place in biofilters of synthetic packaging of the type: plastic, ceramic rings, nylon fiber; among others, given the regular form of support medium; that influences providing a uniform specific surface area and ensuring an adequate intake of residual liquid into the biofilm’s interior. In particular; there are three important functions to the synthetic support medium in OM anaerobic reactors’ performance: 1) ensure the retention of a more concentrated biomass, 2) reduce the biomass’ excessive washing, and 3) allow greater retention of solids in the reactors [10,16,34,39,40,41]. According to [10] the trickling filters that use plastic support means can achieve better performance, but at a substantially higher cost than filters based on stony material. It has also been experimentally observed that the elimination of OM and inorganic matter decreases as the number of steps in it increases through multistage, multilayer filters or through recirculation through a single filter or phase [8,14,25,42-44]. The theoretical formulation proposed in this study presents equations whose structure is derived from a conceptual mathematical model of mass balance (Eq. 1); as well as parameters and variables applied using empirical equations for DI-FAFS and TRI-FAFS (Tables 2 and 3).
Table 2 Proposed equations for the design of an anaerobic up flow filter in two phases (DI-FAFS).

Source: the authors
Table 3 Proposed equations for the design of an anaerobic upflow filter in three phases (TRI-FAFS).

Source: the authors
The Eqs. 10 and 12 have been modified in this study to create empirical relationships for a FAFA of plastic medium, resulting in those indicated in Tables 2 and 3: Eqs. 13 and 17 are based on Eq. of [9] and [42]; Eq. 14 and 15; 18 and 19 are based on Eq. of [8,9,42,45] and Eq. 16 and 20 are based on Eq. of [8,9,42].
Tables 2 and 3 show the four equations proposed to estimate the Se in DI-FAFS’ effluent and four in the TRI-FAFS, respectively being the independent variables: 1) Si: OM in the tributary to the filter in mg COD/l, 2) the relation D1/D2; D1 filter’s depth in phase 1 in m, D2 filter ‘s depth in phase 2 in m, 3) the ratio D2/D3; D3 filter’s depth in phase 3 in m, 4) Sa1: filter’s surface area in phase 1 in m2, 5) Sa2: filter’s surface area in phase 2 in m2, 6) VOC in kg m-3 d-1 and 7) tributary’s T in °C.
Eqs. (13) to (20) include the following variables and parameters: (12): Se, Si, D1/D2 and VOC, k, x, n; (13) and (14): Se, Si, T, D1/D2, VOC, k, A, x, n; (15): Se, Si, D1/D2, Sa1, Sa2, VOC, k, x, m, p, n, (16): Se, Si, D1/D2, D2/D3, VOC, k, x, y, n; (17) and (18): Se, Si, D1/D2, D2/D3, VOC, k, A, x, y, n; (19): Se, Si, D1/D2, D2/D3, Sa1, Sa2, VOC, k, x, m, p, y, n.
4. Results
4.1. DI-FAFS’ statistical adjustment design models results
Table 4 presents the DI-FAFS’ statistical adjustment design models results proposed Eq. (13) to (16), indicating the parameters in the average values and Table 5 shows the adjustments' statistical data and proposed equations for the design of DI-FAFS indicated in the following order: P: number of independent variables, n1: amount of data in the calibration stage, n2: amount of data in the validation stage, R2: coefficient of determination, R2 ajust: adjusted determination coefficient , SEE: Standard Estimation Error, AME: Absolute Mean Error and F0: Statistic test function F. In Eq. (13) to (16) statistics take the sequence’s values presented in the Table 5.
Comparing the statistical values’ results of adjustment from the data obtained for models 13 to 16, we observe: a) the number of independent variables within each proposed equation varied between 3 and 5, b) the amount of data in the stage of calibration varied between 18 and 22, c) the amount of data in the validation stage varied between 5 and 9, d) the coefficient of determination indicates that between 65.93% and 87% of the variation observed in Se is explained by Eqs. (13) to (16), e) the adjusted coefficient of determination is the preference variable in contrast to the coefficient of determination because the equations have between 3 and 5 independent variables, the R2 ajust contributes to assess the contribution in the explanation of the variable’s answer Se from the terms that are added to Eq. (13) to (16) due to the same increase from 3 to 5 of those independent variables. The incorporation of T of the residual water and the surface contact areas on the filter in the two stages (Sa1) and (Sa2) to Eq. (13) results in an increase of R2 ajust; so it can be said that these variables contribute significantly to the Se variable. Accordingly, [46] they indicate that an adjusted coefficient of determination of at least 0.7 is recommended for prediction purposes. Eqs. (14) and (15) resulted in a R2 ajust that varies between 0.7708 and 0.85; whereas Eq. (13) and (16) have resulted with R2 ajust slightly less than 0.7; f) the standard error of estimation was the minimum value in Eq. (15) with respect to Eqs. (13), (14) and (16) and equal to 201.95; representing a better fit of this equation to Se's observations; g) the absolute average error resulted in the minimum value also in Eq. (15) with respect to Eqs. (13), (14) and (16) equal to 135.12; as a result, the best fit of this model for observations; the residuals are smaller with respect to the rest of the equations; consequently AME is smaller, h) the estimated Durbin-Watson (d) statistic results within the range of limits for the dL and dV test selected for a level of significance α = 0.05; resulting in no decision as to whether there is autocorrelation between the consecutive residues; and consequently to the independence of consecutive residuals, i) the comparison of statistic test values and the function’s F critical value results in that in all cases F0 <F (α, k, n-k-1) ; indicating that at least one term or variable in the model has a significant contribution in explaining the response variable Se. From above it is concluded that Eq. (15) is the model that best fits the data; result of a combination of independent variables that estimate values of Se approximated to the experiment’s results.
4.2. TRI-FAFS’ statistical adjustment design models results
The Table 6 presents the TRI-FAFS’ statistical adjustment proposals for design results of Eq. 17 to 20; indicating parameters in average values.
Similarly, Table 7 shows residues adjustment statistics of Eq. (17) to (20) now proposed for TRI-FAFS’ design indicated in the same order.
Comparing the statistical adjustment result values, results obtained for the data to Eqs. (17) to (20), the following is inferred: a) the number of independent variables within each proposed equation varied between 4 and 6, b) the amount of data in the calibration stage were 18, c) the amount of data in the validation stage was equal to 9, d) the coefficient of determination indicates that between 80.92% and 89.93% of variation observed in Se is explained by Eqs. (17) to (20), e) the adjusted coefficient of determination is the preference variable in contrast to the coefficient of determination since the R2 ajust contributes to assess the contribution in the explanation of the response variable Se of terms that are added to Eqs. (17) to (20) due to the same increase from 4 to 6 independent variables. The incorporation of the T of residual water and the filter’s surface contact areas in the two stages (Sa1) and (Sa2) to Eq. (17) result in all the equations values of R2 above 0.8 varying between 0.80 and 0.89 and R2 aju ≥ 0.7 also in all the equations, all fulfilling the criterion indicated above; f) as the TRI-FAFS equations have between 4 and 6 independent variables, R2 ajust contributes to assess the contribution in the explanation of the response variable Se of terms that are added to Eqs. (17) to (20), as the incorporation of T of residual water and the filter’s surface contact areas in three stages (Sa1) and (Sa2) result in a decrease of R2 ajust between 0.73 and 0.84, values higher than those determined for Eqs. (13) and (16) with R2 ajust, but all higher than 0.7, which according to [46] allow to predict and allow to affirm that these variables contribute significantly with the Se variable; g) the standard error of estimation was the minimum value in Eq. (19) with respect to Eqs. (17), (18) and (20) and equal to 44.02; which is less than the SEE found in the model (15) corresponding to 201.95; representing a better fit to the equation to Se observations when comparing the Se estimate equation for the DI-FAFS with respect to the TRI-FAFS. g) the absolute average error resulted in the minimum value in Eq. (19) with respect to Eq. (17), (18) and (20) equal to 28.96; which is less than 135.12 found in the mathematical adjustment of Se to the DI-FAFS’ observation; resulting on a better fit of this model for observation; besides, the waste is smaller compared to the rest of the equations; consequently AME is smaller. h) values’ comparison of statistic test and the critical value function F results in that in all cases F0 <F (α, k, n-k-1); indicating that at least one term or variable in the model has a significant contribution in explaining the response variable Se.
From the results obtained and after the combination of independent variables, Eq. (19) is the model that best fits the TRI-FAFS’ data for design model; since it allows to estimate the values of Se very approximated to the observations derived from the experiment, it even estimates in a more precise way the Se values that the Eq. (15) in the DI-FAFS’ model design.
The Tables 8 and 9 show the residues statistic results statistics of Eqs. (13) to (20) for the design of the DI-FAFS and TRI-FAFS indicated in the following order: p: number of variables independent, n1: amount of data in the calibration stage, n2: amount of data in the validation stage, AMEc: Absolute Mean Error in the calibration stage, AEc: Average Error in the calibration stage, AMEv: Absolute Average Error in the validation stage, AEv: Average Error in the validation.
In comparative form, the following observations can be made regarding statistics of adjustment to models data 13 to 20: a) the number of independent variables within each proposed equation varied between 3 and 6; b) the amount of data in the calibration stage is equal to 18, in Eq. (16) volume 22; c) the amount of data in the validation stage is equal to 9, but in Eq. (16), volume 5; d) the AMEc and AEc statistics have lower values in the calibration stage with respect to the validation stage, e) the AMEc statistics and AEc calibration stage are smaller in models (15) and ( 19) when comparing them with the rest; f) the statistics from the validation stage AMEv and AEv are among the smallest when comparing the models (15) and (19) the rest; which have a similar mathematical structure and coincidence with the independent variables. The comparison of statistics between calibration and validation stages; as well as between models they also give as a result that the models (15) and (19) are the ones that best estimate the response variable Se for DI-FAFS and TRI-FAFS’ design model, respectively. Fig. 1 shows the linear trend of Se/Si against t in four of the depths’ combinations in the DI-FAFS reactor; observing the following cases: 1) when the relation D1/D2 is equal to 4, the tendency of the COD’s remainder with contact time is to decrease, for T equal to 20 and 27°C; changes grow when T rises to 34°C; 2) when D1/D2 ratio is equal to one the DI-FAFS it shows a decreasing trend of remaining COD with contact time when T is 20°C and increasing temperatures between 27 and 34°C; 3) when the ratio D1/D2 is equal to 0.25, the remaining COD has a tendency to increase T between 20 and 27°C; however, it decreases when T is greater than 27°C; 4) as T increases from 20 to 34°C, the remaining COD decreases proportionally, 5) the best tendency for COD removal occurs at 34°C; achieving 72.86% in a reactor where D1/D2 is equal to 0.25 and with an increased VOC from 2.25 to 4.64 kg m-3 d-1, 6) the AME test showed that the pig manure used as inoculum for the DI- FAFS and TRI-FAFS tended to grow and not to adapt to the substrate based on volatile fatty acids (VFA); this could explain that the two phases that make up the DI-FAFS reactor have a high growth of microorganisms producing a COD remnant that varies between 30% and 70%; formed by residual liquid and new cellular material; which could suggest the inclusion of a third phase.
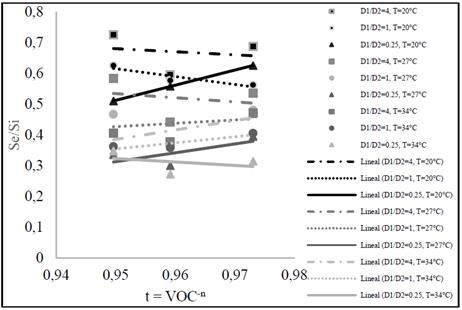
Source: The authors
Figure 1 Remaining COD with respect to VOC-n derived from application of Eq. (15) to experimental observations for DI-FAFS.
In general, in the DI-FAFS’ reactor first phase, tendency should point to an exponential growth of microorganisms that make up the biofilm; since the OM. expressed through VOC should be available in excess. The microorganisms in the biofilm obtain the energy from the processes of anaerobic digestion of OM; and organic carbon is used for the formation of new cellular tissue; so that the OM’ may have a greater proportion of removal efficiency present in the residual liquid. Insofar as the first phase is reduced in depth, the hydraulic load could contribute to creating hydrodynamic conditions so that a fraction of the new cellular tissue detaches from the biofilm and integrates part of the residual liquid to be treated towards the second phase; which could explain the increase in the remaining COD. When entering the second separated phase; biofilm’s microorganisms should have an exponential growth and removal should increase as the depth and contact time augment. The experimental observations lead to the fact that it would be necessary to increase the separated phases, emphasizing the sectioning of the first phase; maintaining the condition of 0.8D in the last phase; to form an anaerobic upflow filter with three separated phases for total depth D. Fig. 2 shows the linear trend of Se/Si against t in all combinations of depths in the TRI-FAFS reactor with residual liquid T of 20, 27 and 34°C; reporting decreasing trend of the remaining COD in the contact time for all temperatures, with removal tending to be above 90% COD.
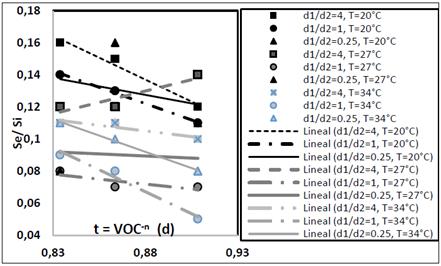
Source: the authors
Figure 2 Remaining COD respecting to VOC-n derived from application of Eq. (15) to experimental observations for TRI-FAFS
Generally; the separated phases in the DI-FAFS and TRI-FAFS reactors seem to influence the microorganisms’ stages of growth within the biofilm and its consequent transformation action on the OM contained in the residual liquid; being able, in the TRI-FAFS case to reach an endogenous phase; that would transform the filter into a digester; this latter TRI-FAFS’ reactor configuration can be considered as hybrid.
Fig. 3 shows the efficiencies of COD removal respecting the VOC, for each reactor type and Fig. 4 shows the removal efficiencies of COQ Vs number of phases of an anaerobic upflow filter, where it is observed that the lowest removal has been found in the UNI-FAFS reactor varying between 50 and 60%; followed by the DI-FAFS reactor between 30 and 80% and the TRI-FAFS between 80 and 95%, results that allow to validate the filter’s division into two and three separate phases, due to the increase observed in the removal of OM (COD) within the phases’ division
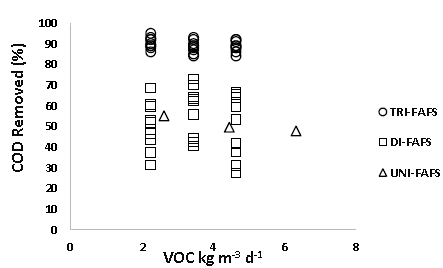
Source: the authors
Figure 3 Chemical Oxygen Removal Demand (COD) respecting VOC for one phase ascendant flow filters (UNI-FAFS), two phases (DI-FAFS) and three phases (TRI-FAFS).
5. Conclusions
Removal of COD in DI-FAFS varied between 27 and 72.86% and between 84 and 95% in TRI-FAFS, finding influence on the filter’s number of stages or phases, when they were operated with VOC between 2.25- 4.64 kg DQO m-3 d-1, T of the residual liquid between 20 - 34°C, HRT of 18 - 16 h respectively, hydraulic surface load of 1.82 m3 m-2 d-1 and with a total depth of 1.2 m, packed with plastic rings with a surface area of 476.35 m2 m-3.
Eq. (13) to (20) formulated to explain DI-FAFS and TRI-FAFS’ reactors operation are the equations’ result of adaptation for trickling filters and anaerobic biofilters, similarity has been found in the magnitude of the T of residual liquid with the values reported by [33] for value k proposed by [45] and the power of the VOC as [35, 18].
Eq. (15) and (19) are proposed for DI-FAFS and TRI-FAFS design respectively, a product from the combination of independent variables; that estimate the values of Se approximated to the observations derived from the experiment, being the independent variables: filters’ depth ratio separated in phase 1 respecting phase 2 (D1/D2) in the two-phase reactor; D1/D2 depth ration in phase 1 with respecting phase 2 (D1/D2) and in phase 2 respecting phase 3 (D2/D3) in the three-phase filters; besides the T of the residual liquid and the VOC, three factors fixed in the experimental design. In both cases, the value of power n gives positive between 0, power substituted in Eq. (15) and (19) represent an equivalent to the time of substrate’s contact t with microorganisms to achieve the removal of DI-FAFS or TRI-FAFS’ affluent substrate; as can be verified in the formulation represented by Eq. (12). Eq. (15) and (18) resulted in an R2 ajust greater than 0.7; the standard error of estimation and the absolute average error resulted in the minimum value in Eq. (15) and (19) with respect to the rest of the equations.
The separated phases in the DI-FAFS and TRI-FAFS reactors seem to influence the microorganisms’ growth stages within the biofilm and the consequent transformation action of the OM’s residual liquid; being able to reach the endogenous phase within the TRI-FAFS; this would transform the filter into a digester; this latter TRI-FAFS‘reactor configuration be considered as hybrid.
Mathematical models proposed in this study are based on trickling filter equations in the activated biofilter variant; whose performance model is developed and has evolved in advective and non-stationary form since 1944 to the present; as an innovation, the adaptation of these to the estimation of yield in the elimination of the OM in the DI-FAFS and TRI-FAFS is considered under the fixed bed type during the first phase and expanded in the second and subsequent phases.
The proposed equations are hybrid, conceptual-empirical type models, where the conceptual model is based on equations deduced from a low mass balance advective dS/dZ(0 and non-stationary dS/dt (0 .
Experimental design conditions are: VOC: 2.25, 3.41 and 4.64 kg m-3 d-1; T: 20, 27 and 34°C; as well as two and three phases separated in series and the parameters obtained from the statistical adjustment are: DI-FAFS: n equal 0.033, contact time: 22 to 23 hours, k: -1.6 to -2.48 d-1 to T = 20°C, k = -1.99 d-1 at T = 27°C, k = - 1.43 d-1 at T = 34°C, Se/Si: 27 and 86%; TRI-FAFS: n equal 0.11, contact time: 19 to 22 hours, k: -0.13 to -0.56 d-1 to T = 20°C, k = -0.13 d-1 to T = 27°C, k = -0.13 to -0.56 d-1 at T = 34°C; Se/Si: 84 and 95%.
Results found are comparable in terms of the T of the residual liquid to be treated; specifically for T of 20°C and a maximum extreme case when T is 34°C; which is tested only by this study; confirming that there is dependence on T with the constant of biological reaction’s speed; which influences not only the metabolic activities of microbial population; with a profound effect on the gas transfer rate (CH4 and CO2) in the anaerobic process and on the sedimentation characteristics of biological sludge; hence, this variable is a significant factor in Eq. (15) and (19) proposals.
Phases of hydrolysis, acidogenesis and methanogenesis associated with an anaerobic process according to Metcalf and Eddy, (1996) could have occurred given the high removal of OM obtained in the TRI-FAFS reactor; that could be confirmed in subsequent studies with a sampling of bacterial prevalence in each phase.

































