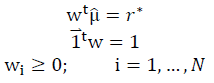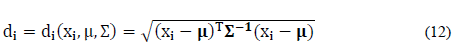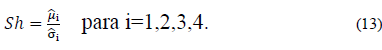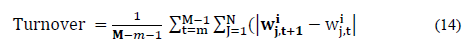1. Introducción

La selección de portafolios consiste en distribuir el capital de inversión entre un conjunto activos, la forma de distribuir este capital ha sido un tema de gran interés entre los gestores de carteras. La teoría clásica de selección de portafolios data desde el año 1952, cuando Harry Markowitz presentó el modelo no lineal para la optimización de portafolios conocido como Media-Varianza (M-V), que se presenta en la ec. (1) y consiste en asignar capital sobre una cantidad de activos disponibles para maximizar el retorno de la inversión mientras se minimiza el riesgo asociado, generando de esta forma carteras que no pueden ser mejoradas en términos de rentabilidad y riesgo, y son llamadas eficientes [¹³].

Sujeto a:

Donde w es el vector de pesos del portafolio, es el vector que estima la rentabilidad media de los activos, es el estimador de la matriz de varianzas y covarianzas, N es el número de activos que conforman el portafolio, r^* es el rendimiento esperado del portafolio y γ indica el grado de aversión al riesgo del inversionista.

Es de anotar que la rentabilidad y la varianza del portafolio, en el modelo clásico son estimados mediante el método de máxima verosimilitud, el cual supone, que los rendimientos presentan una distribución de probabilidad normal [¹⁷], lo que proporciona estimadores fáciles de construir y provee estimaciones insesgadas, sin embargo tienen comportamientos indeseables bajo un escenario de una distribución no normal de las variables aleatorias, y especialmente cuando el número de variables es mayor o igual a la cantidad de observaciones de la muestra , ya que no minimiza el error cuadrático medio, provee estimaciones sesgadas y el cálculo matemático de la estimación resulta ser más complejo.

El alejamiento entre una serie histórica de rendimientos y una distribución normal, ocasiona que la estimación de los parámetros sea influenciada por colas marginales pesadas [¹⁷], lo anterior, es importante para la selección de la carteras, dado que una amplia evidencia indica que la distribución empírica de los rendimientos por lo general se desvía de la distribución normal, produciendo un error de estimación, que ocasiona fluctuaciones sustanciales en los pesos resultantes de la cartera en el tiempo [¹,³,⁴].

Se ha estudiado que los portafolios construidos con base en el modelo clásico de M-V presentan mayor error de estimación que aquellos que son conformados con base al modelo de mínima varianza, dado que gran parte de la inestabilidad de las carteras construidas con el modelo M-V se debe a la estimación de los rendimientos medios de los activos, esta afirmación está respaldada por una amplia evidencia empírica que muestra que la cartera de mínima varianza normalmente obtiene mejores resultados fuera de la muestra que cualquier otra cartera de media-varianza [⁴].

Los portafolios de mínima varianza equivalen a los portafolios de M-V cuando el parámetro de aversión al riesgo tiende a infinito, además, para implementar esta política sólo se utiliza la estimación de la matriz de varianzas y covarianzas de las rentabilidades, con lo cual, las ponderaciones óptimas de esta estrategia son más estables y fluctúan menos en cada rebalanceo, respecto a las ponderaciones calculadas con la política M-V [¹⁸].

El modelo de mínima varianza busca minimizar la varianza del portafolio de inversión, siempre y cuando la totalidad del capital de inversión sea asignado en los activos que lo conforman [⁴,⁵]. El problema de optimización de mínima varianza es representado mediante en la ec. (2).

sujeto a:

Donde es el vector de pesos de la cartera, es la matriz de covarianza estimada, es la varianza del rendimiento de la cartera, es la vector de unos, y la restricción asegura que los pesos de la cartera sumen uno, es decir, indica que el inversionista gasta exactamente el capital disponible [¹⁴].

Pese a que los portafolios conformados con el modelo de mínima varianza presentan menor fluctuación en la asignación de los pesos de los activos del portafolio, su sensibilidad ante error de estimación es considerable, debido a que la estimación de la matriz covarianza habitualmente también es realizada a partir del método de máxima verosimilitud [³]. Con el fin de mitigar el error de estimación ocasionado por la presencia de datos atípicos se ha encontrado en la literatura especializada que el uso de la estadística robusta para la estimación de parámetros en datos que no siguen estrictamente una función paramétrica, permite obtener resultados mas sólidos e insensibles frente a la presencia de datos atípicos [²,⁶].

Con base a lo anterior, es pertinente conocer que los estadísticos robustos evalúan los cambios en las estimaciones debido a pequeños cambios en las suposiciones básicas y crea nuevas estimaciones que son insensibles a pequeños cambios en algunos de los supuestos de los modelos estadísticos, éstos, cambian los criterios de optimización con respecto a la estadística clásica, ya que ésta busca mayor estabilidad y menor sensibilidad a cambios bruscos en los datos [³], es por ello, que la estimación robusta es usada en la asignación de pesos en una cartera con el fin de minimizar el error de estimación.

Con el fin de inducir una mayor estabilidad en los pesos asignados a los activos que conforman un portafolio de inversión, en este artículo se estudian las carteras de mínima varianza bajo la metodología rolling horizon, para lo cual, se propone un método de estimación robusta y no paramétrica de la matriz de covarianza a partir de las bases teóricas del recorte de la media y del encogimiento de la misma para portafolios de gran tamaño. Adicionalmente, se estudian los métodos de estimación robusta de la matriz de covarianza llamados determinante mínimo de la matriz de covarianza-MCD y el recorte chi-cuadrado en la distancia de Mahalanobis, que si bien, ya se encuentran introducidos en la literatura, hasta nuestro conocimeinto no se encontraron estudios aplicados para la selección óptima de carteras de inversión de mínima varianza.

Este artículo presenta el desempeño financiero de cuatro portafolios de inversión de diferente dimensión en términos del ratio de sharpe, del índice de turnover y de la varianza de los mismos, que fueron obtenidos, con los métodos de estimación de la matriz de covarianza indicados en el párrafo anterior. Los resultados asociados al desempeño financiero de los portafolios, se compararon con del estudio de referencia llamado “A generalized approach to portfolio optimization: improving performance by contraining portfolio norms” [⁴].

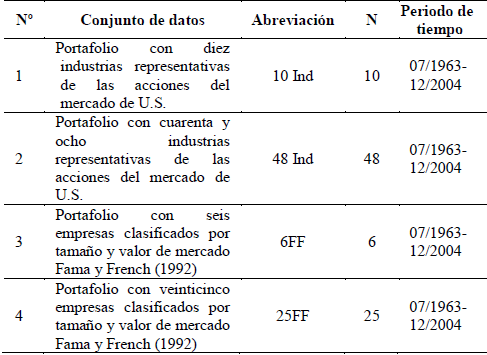
Es importante anotar que en el estudio de referencia, los autores buscan resolver el error de estimación generado con el modelo de varianza mínima mediante la imposición de una restricción adicional que consiste en establecer una norma al vector de pesos del portafolios de tal forma que sea inferior a un umbral determinado, por lo cual proponen ocho nuevas carteras con diferentes normas y se comparan con cinco estrategias de selección de portafolios introducidas en la literatura. En la Tabla 1 se presentan las diferentes estrategias estudiadas en el estudio de referencia.

Tabla 1 Descripción abreviaturas de las estrategias desarrolladas en el estudio de referencia 

Fuente: Adaptado de [⁴]

2. Metodología

2.1. Descripción de los datos

Los datos que se utilizaron se encuentran disponibles en el portal web de Kenneth R. French [⁷], donde se proporciona las rentabilidades históricas diarias, mensuales, y anuales de diferentes carteras conformadas por acciones pertenecientes a las bolsas de valores NASDAK, NYSE y AMEX de Estados Unidos. Para este estudio se seleccionaron carteras con rentabilidades históricas mensuales dado que son las que se utilizaron en el estudio de referencia.

La evaluación del desempeño financiero de los portafolios estudiados en este artículo, se realizó mediante el benchmarking de los resultados del ratio de sharpe, del índice de turnover y de la varianza de los portafolios seleccionados con los métodos estudiados en este artículo y con los resultados del estudio de referencia. Por lo tanto, se hizo necesario generar condiciones de igualdad en la base de datos y temporalidad. Ver Tabla 2. Se analizaron cuatro portafolios de diferente dimensión que presentan dos enfoques diferentes, el primero de ellos se basa en portafolios conformados por acciones de la industria de las bolsas de valores mencionadas anteriormente, y el segundo enfoque se basa en carteras conformadas de acuerdo al tamaño y al valor de mercado de los activos.

Tabla 2 Conjunto de datos 

Fuente: Adaptado de [⁴]

2.2. Estimación de las matrices de covarianza

La selección de portafolios de mínima varianza se realizó bajo la metodología rolling horizon que se compone de dos momentos llamados in-sample y out-sample, para lo cual se desarrolló un algoritmo iterativo en el software Matlab_R2018. El primer momento in-sample, consistió en la elección de una ventana móvil invariable con un tamaño de 120 observaciones que para los datos mensuales de los portafolios correspondió a 10 años, en el momento out-sample, la ventana que se seleccionó en cada iteración se desplazó un periodo hacia delante entre el conjunto total de datos, de manera que se eliminó la última observación y se agregó la observación mas reciente, de esta forma el algoritmo iteró 378 veces, dado que el total de datos fue de 498. Lo anterior permitió realizar estimaciones mas acertadas debido al entrenamiento del algoritmo que se basa en tomar la información reciente de los datos y en eliminar la mas antigua.

Dentro del algoritmo iterativo out-sample de la metodología rolling horizon, se desarrolló el modelo de mínima varianza para lo cual fue necesario la estimación de la matriz de covarianza, que se estimó mediante la implementación de tres diferentes métodos robustos, el primero es la gran contribución de este artículo que consiste en el encogimiento de la matriz de covarianza con recorte a la media, el segundo y tercer método son recorte chi-cuadrado en la distancia de Mahalanobis y el Determinante Mínimo de la Matriz de Covarianza (MCD) respectivamente.

2.2.1. Método propuesto: encogimiento de la matriz de covarianza con recorte a la media

El modelo propuesto de estimación robusta permite calcular dos matrices de covarianza denotadas por y , las cuales se basan en la aplicación conjunta de la teoría robusta de la media recortada y de la teoría de encogimiento o “shrinkage” de la varianza propuesto por Ledoit O. & Wolf M. en el año 2003. El modelo estadístico, y la descripción para la estimación de y es:

Sea X_Nxp, un matriz de p rendimientos de las acciones que conforman un portafolio de inversión compuesto por N variables aleatorias, que representan la cantidad N de activos.

Se asume los siguientes supuestos iniciales:

• El rendimiento de los N activos son independientes e idénticamente distribuidos en el tiempo.

• El portafolio de inversión es seleccionado mediante la estrategia de optimización de mínima varianza.

• El portafolio de inversión permite ventas en corto de los N activos.

Cuando la dimensión de la matriz es grande en comparación con el tamaño de la muestra, lo que ocurre con frecuencia, la matriz de covarianza muestral se encuentre mal acondicionada. El estimador shrinkage propuesto por Ledoit O. & Wolf M en el año 2003 esta bien condicionado, permite el cálculo de la inversa de la matriz de covarianza y es aplicable para matrices de gran dimensión.

El estimador de contracción o shrinkage tiene tres componentes: un estimador sin estructura S, un estimador con mucha estructura denotado por F y una constante de contracción λ. El método estadístico de encogimiento de la matriz de covarianza sugiere imponer alguna estructura en un problema de estimación de gran tamaño. El objetivo central del método es reducir mediante la constante óptima de contracción, la matriz de covarianza de la muestra S, no sesgada pero muy variable, hacia la matriz de covarianza estructurada F y obtener así un estimador más eficiente [⁹-¹¹]

La matriz de covarianza muestral se considera en el modelo como un estimador no estructurado ya que no se impone ninguna estructura pues representa la información de los datos [⁹,¹¹]. Con el fin de estimar una matriz de covarianza de la muestra que sea robusta y aplicable a portafolios de gran tamaño, donde es posible el caso en que N ≤ p, se propone una estimación basada en la teoría de la media recortada que permite excluir datos atípicos de los rendimientos de las acciones.

Con la media recortada se obtiene una estimación más representativa del centro del cuerpo de los datos, adicionalmente, excluye un porcentaje de los valores mas altos y mas bajos. El cálculo de la media recortada se realizó mediante la ec. (3).

Donde:

N: número de observaciones ordenadas de manera ascendente.

α: es la proporción de casos a eliminar en cada extremo de la distribución.

g: número de observaciones que deben ser eliminadas.

Con g = [αt] ,donde [ ] denota la parte entera resultante de la operación.

x_i: serie de observaciones.

Habitualmente, la matriz de covarianza se calcula mediante la ec. 4, Donde N indica la cantidad de observaciones de cada variable, r _ki corresponde al rendimiento k del activo i para n = 1,2, …,N y es el estimador de la rentabilidad media de los activos.

Se tiene que la matriz de covarianza robusta de la muestra con recorte de la media se encuentra definida por la ec. (5), que es el resultado de reemplazar la ec. (3) en la ec.(4).

Para t =1,…,N y con también son recortes en la matriz de covarianza a un nivel α.

Posteriormente, la ec. (6) representa el factor de corrección (FC) que se aplicó a la matriz de covarianza S_r.

Donde D convierte en una matriz diagonal el factor de corrección aplicado a la matriz S_r . En consecuencia el cálculo presentada en la ec. (7), es la estimación robusta de la matriz de covarianza muestral, la cual, tiene implicado un factor de corrección.

La estimación de la matriz de covarianza objetivo busca estar bien condicionada, es decir, con poco sesgo y con un error de estimación que no aumente cuando se determina la inversa de la matriz de covarianza [⁹], adicionalmente, una forma de obtener un estimador estructurado bien condicionado es imponer la condición de que todas las varianzas sean las mismas y todas las covarianzas sean cero.

Con base en lo anterior, la matriz objetivo se calculó con base en el siguiente planteamiento: F _n se define como F _n 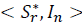entonces E[F _n ] = µ _n , en consecuencia, F_n = Target matrix = µI, donde µ en el método desarrollado en este artículo, corresponde al promedio del conjunto de datos de la diagonal principal de la matriz de covarianza de la muestra e I_n es la matriz identidad de orden n para todo n=1,…, N[¹⁰].

La estimación de la constante óptima de contracción requiere del uso de un estimador consistente, es decir, que se aproxime al verdadero valor de la constante de contracción a medida que el tamaño de la muestra aumenta. Este estimador se calculó mediante la ec. (8).

Donde P, r y c son parámetros consistentes. El parámetro P estima consistentemente a Π, el cual, denota la suma de las varianzas asintóticas de las entradas de matriz de covarianza robusta de la muestra 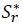. El parámetro r es el estimador consistente de ρ, el cual, indica la suma de las varianzas asintóticas de las entradas de la matriz estructurada u objetivo Fn con las entradas de la matriz de covarianza robusta de la muestra 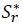. Por último, el parámetro c es el estimador consistente de Γ que denota la mala especificación o el error de estimación del modelo utilizado en la matriz objetivo.

Una vez fueron calculadas las matrices 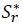y F y la constante de óptima de contracción λ*, se procedió a determinar la matriz shrinkage de covarianza de los rendimientos de las acciones, a través de la ec. (9).

Posteriormente, se emplearon las matrices de covarianzas estimadas 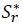y 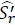como parámetros del modelo de selección de portafolios de mínima varianza.

2.2.2. Determinante mínimo de la matriz de covarianza -MCD

La implementación del método del determinante mínimo de la matriz de covarianza en el algoritmo out sample, se basó en el método propuesto por Rousseauw P.J en el año 1984, el cual, es uno de los estimadores pioneros equivariantes y altamente robustos de localización y dispersión multivariada [²¹,¹⁰], su objetivo es encontrar h observaciones cuya matriz de covarianza tenga el determinante más bajo [²⁰], concretamente, el algoritmo propone una matriz de covarianza de determinante mínimo para la detección de datos atípicos mutilvariantes, que posee propiedades asintóticas que hacen posible la comparación con otros estimadores con puntos de ruptura altos [¹⁹].

Para la estimación de la matriz de covarianza por este método se seleccionó un sub-muestra denominada x _MCD de tamaño h desde tal qu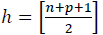e donde y p corresponde a las cantidad de variables, posteriormente se calcularon las matrices de covarianza de cada una de las sub-muestras 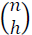de tamaño h, seguidamente se calculó el determinante de cada una de las matrices obtenidas en el paso anterior y finalmente se eligió la sub-muestra con la que obtuvo el determinante más bajo en la matriz de covarianza para así calcular el estimador de la matriz de covarianza mediante la ec. (10):

Donde c(h), corresponde al factor de consistencia que se presenta en la ec. (11), este factor hace que el estimador de la matriz de covarianza tienda a una distribución Fisher consistente, cuando la distribución es elíptica y unimodal, por ejemplo, .

Una vez fue calculada la matriz de covarianza por el método MCD se procedió a emplearla como parámetro en el modelo de selección de mínima varianza en cada uno de los portafolios estudiados en este artículo.

2.2.3. Recorte chi-cuadrado en la distancia de Mahalanobis.

La distancia de Mahalanobis permite detectar datos atípicos multivariantes, a partir de la descripción de la distancia entre cada punto de datos y del centro de masa de los mismos. Cuando un punto se encuentra distante del centro de masa, se considera como un valor atípico [¹⁵] [¹²], el cálculo de esta distancia se realizó mediante la ec. (12).

Donde x es un vector de variables, es un vector y Σ es la matriz de covarianza simétrica de dimension k x k.

En consecuencia con lo anterior, el cálculo de la matriz de covarianza por este método consistió en la detección de datos atípicos multivariantes, a partir del recorte chi-cuadrado en la distancia Mahalanobis, por lo que fue necesario ordenar las distancias de menor a mayor, posteriormente, se determinó con un 10% de probabilidad las distancias de Mahalanobis inferiores al valor correspondiente de la distribución inversa chi-cuadrado con un 90% de probabilidad y p grados de libertad. Es de anotar que p, corresponde a la cantidad de variables del portafolio sometido en el proceso de simulación. Las distancias de Mahalanobis que cumplieron la restricción anterior, se ordenaron y posteriormente se calculó la matriz de covarianza, la cual se denotó .

Una vez, calculada la matriz de covarianza se utilizó como parámetro del modelo de mínima varianza la selección de los portafolios de inversión.

2.2. Descripción de la metodología usada para la evaluación financiera de los portafolios

Para el análisis del desempeño financiero de los portafolios de inversión, fue necesario utilizar la estimación robusta de la matriz de covarianza calculada por medio de los métodos expuestos anteriormente. Posteriormente, se procedió en la selección de los portafolios de mínima varianza de diferente dimensión y de esta forma dar paso a la evaluación financiera de las carteras en términos del ratio de sharpe, el índice de turnover y la varianza.

Para el análisis del ratio de sharpe de los portafolios construidos con la estimación de la matriz de varianzas y covarianzas mediante el método propuesto de encogimiento de matriz de covarianza con recorte a la media, fue necesario realizar previamente la selección del percentil de recorte ( óptimo, el cual permite obtener el mayor valor del ratio de sharpe en cada uno de los portafolios estudiados.

En consecuencia con lo anterior, se realizó el ejercicio de evaluar el valor que toma este indicador de los portafolios en cada percentil de recorte (, donde ( tomó el valor del 1%, hasta el 50%, por ejemplo, si (=20% indica que el recorte de los datos den cada extremo corresponde al 10%, este hecho sucede para los estimadores y 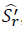, con el fin de determinar el mayor valor del ratio de sharpe alcanzado.

El cálculo del ratio de sharpe en este artículo no supone la presencia de un activo libre de riesgo por lo tanto, la rentabilidad de los portafolios estudiados por unidad de riesgo en un ambiente rolling horizon se determinó mediante la ec. (13).

Donde i indica el método de estimación de la matriz de covarianza utilizado para la selección de portafolios de mínima varianza, es decir, cuando i=1 se indica el portafolio de mínima varianza con la estimación de la matriz de covarianza 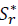, cuando i=2 se refiere al portafolio de mínima varianza con la estimación de la matriz de covarianza, en el caso de que i=3 se indica el portafolio de mínima varianza con la estimación de la matriz de covarianza S _MCD y cuando i=4 indica que se seleccionó el portafolio de mínima varianza con la estimación de la matriz de covarianza .

En el índice de turnover de estabilidad calculado bajo enfoque de rolling horizon, se utilizó como indicador de la dinámica constante de los pesos asignados a los activos de la cartera en cada rebalanceo; para lo cual se utilizó la siguiente ec.(14) que también es porpuesto en [⁵]

Donde, corresponde al peso del activo j del portafolio en el tiempo t de la estrategia i y la expresión del corresponde al peso de la cartera después del rebalanceo en el tiempo t+1 y M corresponde a la serie de los rendimientos de los portafolios y m fue la ventana de estimación

Por último la varianza de los portafolios estudiados bajo la metodología rolling horizon se calculó a partir de la ec.(15), donde r_t+1 corresponde al rendimiento del portafolio en la iteración t+1 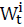, indica el peso de los activos en la iteración t el portafolio i de mínima varianza.

3. Resultados

En la Tabla 3 se muestran los valores que generan mayor rentabilidad por unidad de riesgo (ratio sharpe) obtenidos por los portafolios mediante el método de encogimiento de la matriz de covarianza con recorte a la media de los rendimientos de los portafolios, así como también el ( óptimo asociado.

Tabla 3 Mayor valor de sharpe y el ( óptimo según la dimensión del portafolio 

Fuente: los autores

Se observa en la Tabla 4, que en términos del ratio de sharpe los métodos estudiados en este artículo, que la estimación de las matrices de covarianza para la selección de portafolios superan notablemente el panel B de la sección-B, en especial los valores del ratio de sharpe de los portafolios de mínima varianza de dimensión 10Ind, 48Ind, 6FF y 25FF obtenidos con el método encogimiento de la matriz de covarianza con recorte a la media.

Tabla 4 Ratios de sharpe 

Fuente: Los autores y adaptado de [⁴]

Se destaca además, que los resultados del panel A de la sección-B del portafolio 6FF del estudio de referencia son superadas por las estrategias MIN- , MIN-SMCD y MIN- en al menos el 75%. Por último, en terminos del ratio de sharpe, se hace notorio, que el promedio global de las estrategias MIN- y MIN- 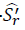en los portafolios estudiados, suministró mejores valores del ratios de sharpe que aquellos plasmados en la sección-B, indicando que los portafolios de mínima varianza estimados con el método propuesto de encogimiento de la matriz de covarianza con recorte a la media, proporcionan mejores rendimientos en relación al riesgo asumido por el inversionista.

La comparación en términos del índice del turnover entre los resultados que se obtuvieron con las estrategias propuestas en este artículo (Sección-A) y las estrategias desarrolladas en la literatura (Sección-B), se destaca que el método propuesto de encogimiento de la matriz de covarianza con recorte a la media de los rendimientos de los portafolios de inversión estudiados en este artículo, proporciona en general valores mas bajos del índice de turnover respecto a los valores presentados en el estudio de referencia, lo que indica que con el empleo de las estrategias MIN- y MIN- 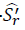es posible brindarle al inversionista mayor credibilidad, debido a que existe mayor estabilidad en la asignación de los pesos en cada activo periodo a periodo del rebalanceo del portafolio.

Con base en la Tabla 5, se puede decir que la estrategia MIN- superó en un 50% las estrategias planteadas en en panel B y en un 100% las estrategias planteadas en el panel A de la sección B, por su parte los portafolios seleccionados con la estrategia MIN- obtuvieron un mejor desempeño en terminos del índice de turnover en el panel A, donde, las estimaciones en los portafolios 10Ind, 48Ind, 6FF, 25FF superaron el 80.50%, 62.50%, 100% y 100% respectivamente los valores de las estrategias estudiadas en el estudio de referencia. Respecto al panel B de la sección A la estrategia MIN- supero en un 50% los índices de turnover correspondientes a los portafolios 48Ind y 25Ind, por otra parte, el índice de turnover del portafolio seleccionado mediante la estrategia MIN-S _MCD superó también en un 50% el índice de turnover de las estrategias del estudio de referencia de los portafolios de 6FF y 25FF, mientras que los portafolios 10Ind y 6FF seleccionados mediante la estrategia MIN- superaron en un 50% y 75% los valores del índice de turnover del estudio de referencia del panel A de la sección B.

Tabla 5 Índices de turnover 

Fuente: Los autores y adaptado de [⁴]

La Tabla 6, en la sección-A se presenta la varianza de los portafolios seleccionados con las estrategias de estimación de la matriz de covarianza propuestas en este artículo y en la Sección-B se muestran los resultados que obtuvieron los autores en el estudio que es considerado referencia en este estudio.

Tabla 6 Varianzas 

Fuente: Los autores y adaptado de [⁴]

De la comparación de los resultados de la varianza de los portafolios estudiados entre las estrategias de la Sección-A y las estrategias comprendidas en la Sección-B, se resalta que los inversionistas y por ende los gestores de las carteras de inversión buscan una varianza pequeña en sus portafolios ya que esto implica menor riesgo, con base en estos términos, de la Tabla 6, se puede decir que los portafolios de mínima varianza obtenidos con los métodos propuestos en este artículo (sección-A) los y conformados por 10 acciones superaron las varianzas de los portafolios pertenecientes al panel A de la sección B el 100%, 100%, 12.5%, 100% respectivamente, y respecto a las varianzas del panel B de la sección B, los portafolios de la sección-A obtuvieron varianzas superiores en un 100%, 50%, 100%, 100% respectivamente.

Así mismo, los portafolios de mínima varianza y con dimensión de 48 acciones, obtenidos con las estrategias planteadas en la sección-A obtuvieron un mejor desempeño en términos de la varianza que el desempeño obtenido en los portafolios de la sección-B, dado que su desempeño en promedio fue superior en el panel-A en un 87.5%, 87.5%, 100%, 100% respectivamente y en el panel-B en un 100% con todos los métodos propuestos. Por otra parte las carteras obtenidas con los métodos propuestos en la sección-A con una dimensión 6 acciones obtuvieron resultados destacables respecto a los resultados plasmados en la sección B, ya que obtuvieron un menor valor en la varianza del portafolio, se destaca que con el uso de las estrategias MIN- , MIN- y MIN- los portafolios supereraron en promedio el 100% las varianzas del panel A y del panel B de los portafolios de la sección-B, mientras que con el empleo de la estrategia MCD, las estrategias estudiadas en este artículo superaron en promedio del panel A el 12.5% y del panel el 100%.

Por otro lado, los portafolios de 25 acciones generados con las estrategias de la sección A superaron en un 100% las estrategias del panel A y del panel B de la sección B con la implementación de la estrategia MIN- , mientras que con la implementación de la estrategia MIN- SMCD superaron del panel A el 12.5% y del panel B obtuvieron menor varianza en un 100%, ademas, con las estrategias MIN- y MIN- se obtuvo que tuvieron en promedio un mejor desempeño del 64.29% y del 14.29% respectivamente.

4. Conclusiones

El método introducido de encogimiento de la matriz de covarianza con recorte a la media es sencillo y presentó un desempeño financiero competitivo en términos del rendimiento por unidad del riesgo, de la estabilidad en la asignación de los pesos de los activos dentro del portafolio de inversión ocasionado de esta forma que se generen menores costos de transacción en el proceso de compra y venta de activos. En términos de la varianza de las carteras se obtuvo resultados deseables y competitivos, lo que permitió obtener portafolios de mínima varianza mas sólidos ante la presencia de datos atípicos.

Por otra parte, el desarrollo del algoritmo para la selección de portafolios de mínima varianza a partir del uso de los métodos robustos de estimación de las matrices de varianzas y covarianzas (encogimiento de la matriz de covarianza con recorte a la media y recorte chi-cuadrado en la distancia de Mahalanobis) presenta eficiencia computacional para portafolios de gran dimensión.