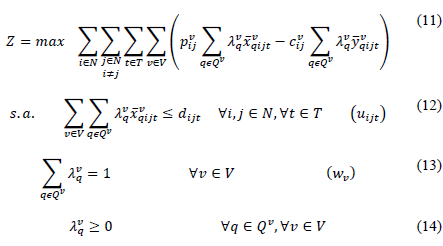English (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
1. Introducción
El problema de la gestión de flotas en el transporte por carretera presenta varios desafíos operacionales, principalmente en la gestión del transporte de transferencia entre terminales, en el cual vehículos son asignados para atender la demanda por transporte de carga. Dada la dispersión geográfica por demanda de servicios de transporte de carga, es común que se acumulen vehículos vacíos en lugares donde no son necesarios o se gene-re una escasez de vehículos donde son necesitados a lo largo del horizonte de planeación. Si bien el desplazamiento de vehículos vacíos no genera lucros para las empresas (los costos operacionales son cubiertos por los viajes de vehículos con carga), estos son necesarios para la continuidad de las operaciones de transporte. Consecuentemente, la asignación de vehículos de carga es un componente central en el planeamiento y control de las operaciones de empresas de transporte de carga por carretera. En este contexto, aparece el Problema de Asignación de Vehículo (PAV), que consiste en, dado un conjunto de demandas conocidas por transporte de carga entre terminales (centros de almacenamiento o distribución), asignar vehículos vacíos a los terminales para atender la demanda, de tal forma a maximizar el lucro generado por los servicios completados y minimizar los costos de viajes de vehículos vacíos.
En [1] se aborda por primera vez el problema de asignación de vehículos en el contexto de transporte de carga por carretera. Basado en modelos previos, los autores proponen una red de espacio-tiempo para representar el aspecto dinámico del problema. En [2] se propone un modelo que incorpora la posibilidad de mantener inventario de vehículos vacíos en los terminales. Las decisiones a ser tomadas corresponden al desplazamiento de vehículos con carga, vehículos vacíos y el inventario de vehículos vacíos en los terminales. En [3] se presenta una taxonomía del problema de asignación de vehículos vacíos, pretendiendo ampliar el conocimiento de estos sistemas e identificar posibles tendencias de investigación relacionada. Los autores presentan una clasificación basada en el alcance y cobertura de los problemas, que consideran más pertinentes para el estudio de reposicionamiento de vehículos: modelos operacionales y modelos de políticas de decisión. Igualmente, definen diferentes criterios que sirven para perfilar la diferente clasificación de los modelos.
En [4] se estudia el PAV con demanda incierta con el objetivo de maximizar el margen de contribución neto esperado. El problema es formulado como un modelo de programación estocástica, y una nueva heurística es desarrollada, la cual es comparada como aproximaciones determinísticas previas. En [5,6] se presenta una formulación de modelaje denominada Logistics Queueing Networks (LQN) para la gestión de cargas en un sistema operacional, basado en el trabajo de [7]. Las formulaciones clásicas basadas en programación lineal de problemas reales generalmente resultan en modelos intratables. No obstante, los modelos LQN pueden considerar una cantidad mayor de detalles del problema, contrariamente a las formulaciones clásicas. Los autores muestran que el algoritmo LQN se aproxima alrededor de 3% de los valores óptimos de la relajación lineal.
En [8-10] se estudia el PAV en el contexto de sistema de transporte de carga por carretera en Brasil. Los autores toman como punto inicial el modelo de [11] y acrecentan detalles importantes en la gestión de vehículos de carga, como la necesidad de tercerización de flota (outsource fleet sizing), la necesidad de aceptar backlog (como consecuencia del alto nivel competitivo en la industria de carga, es estratégicamente perjudicial rechazar pedidos), diferentes tipos de vehículos, restricciones de desplazamiento de vehículos para ciertas cargas o ciertos trayectos, y capacidad de carga en los terminales. El énfasis es dado en la caracterización del problema en situaciones reales, en la modelación matemática del problema y la utilización de heurísticas y metaheurísticas como GRASP, simmulated annealing y colonia de hormigas (ACO), para obtener soluciones factibles.
Considerando la dificultad computacional para resolver ejemplares realistas de gran porte del PAV por medio de software de optimización de propósito general, como IBM CPLEX, este trabajo contribuye con la generación de cotas ajustadas para el PAV a través de técnicas de decomposición, como relajación lagranjeana y decomposición Dantzig-Wolfe, para tratar problemas de gran porte y proporcionar cotas de buena calidad para el PAV. Cabe la pena resaltar, que estas cotas sirven para evaluar la calidad de soluciones generadas por métodos heurísticos, los cuales no generan certificados de calidad de las soluciones por si solos.
El resto de este artículo está estructurado de la siguiente forma. Inicialmente, se define un modelo de programación lineal entera para el PAV. Luego, se presenta los métodos de decomposición utilizados para resolver el problema. Posteriormente, se presenta resultados computacionales para ejemplares realistas de gran porte. Finalmente, las conclusiones y perspectivas de trabajos futuros son planteados. Las Tablas 1 a 3 defines las variables y parámetros utilizados en el modelo.
2. Modelo Matemático del PAV
Las decisiones a ser tomadas en el PAV implican determinar cuáles cargas son aceptadas y cuales son rechazadas entre los diferentes terminales, además de definir el reposicionamiento de vehículos vacíos entre terminales para atender la demanda futura. A seguir, el PAV es modelado como en [9,10], el cual es una extensión de un problema de flujo multicommodity de costo mínimo en un grafo direccionado de espacio-tiempo, para el caso en que todas las demandas son conocidas a priori. Este problema es conocido por pertenecer al grupo de problemas NP-hard [12].
La función objetivo (1) maximiza el lucro total de las operaciones a lo largo del horizonte de planeación, que equivale al ingreso generado por el desplazamiento de vehículos cargado menos los costos de desplazamiento de vehículos vacíos. El conjunto de restricciones (2) garantiza el equilibrio de flujo de vehículos cargados y vehículos vacíos en cada terminal i, periodo 𝑡 y vehículo tipo v. El conjunto de restricciones (3) establece una cota superior equivalente a la demanda del número de vehículos en cada arco (i,j,t). El conjunto de restricciones (4) establece las rutas permitidas para vehículos cargados y vacíos. Estas restricciones son relevantes desde el punto de vista práctico, pues permiten que ciertos tipos de vehículos realicen ciertas rutas, sea por seguridad de las carreteras, restricciones impuestas en el contrato de los conductores, entre otros. Finalmente, el conjunto de restricciones (5) imponen el dominio de las variables de decisión.
En ciertas situaciones prácticas, es deseable tratar cada vehículo individualmente como un tipo de vehículo, en vez de separarlos en grupos. Esto se hace con el objetivo de mejorar el proceso de planeación de los recursos de operación [9,10]. De esta forma, cada vehículo es considerado como un grupo diferente y se fija 
V, como un parámetro binario, tomando el valor de 1 si el vehículo v entra en el sistema en el terminal i, en el periodo v, y 0 caso contrario, satisfaciendo:
A medida que el número de tipo de vehículos aumenta, la dificultad para resolver la formulación (1)-(5) por métodos convencionales aumenta, debido al crecimiento del número de variables y restricciones en las formulaciones.
3. Métodos de solución
Dado que las heurísticas solo proporcionan cotas inferiores de la solución óptima, no es posible establecer una garantía de óptimalidad por medio de estos métodos. Esto presenta una desventaja desde el punto de vista administrativo y operacional, ya que las empresas necesitan evaluar el valor o desempeño de las decisiones a ser tomadas. Además, el uso de software de optimización de propósito general, que proporcionan certificados de optimización, resulta inviable dada la cantidad de variables y restricciones de los modelos de las formulaciones clásicas. Así pues, en este trabajo se propone explorar la estructura en bloque del modelo propuesto para aplicar dos técnicas de reformulación que, en teoría, permiten garantizar la optimización para instancias de gran porte que no pueden ser resueltas por software de optimización de propósito general. Estas técnicas son: relajación lagranjeana y decomposición de Dantzig-Wolfe.
3.1. Relajación Lagranjeana y optimización por Subgradiente
En esta sección se presenta la relajación lagranjeana y el método de optimización de subgradiente. Iniciando con la reformulación, observe que la función objetivo (1), junto con las restricciones (2), (4) y (5) forman un problema de flujo de costo mínimo, el cual puede ser resuelto de forma eficiente [12]. De esta forma, se penaliza la función objetivo con las restricciones (3) y los multiplicadores lagranjeanos 
(≥0) para todo 
, resultando el problema lagranjeano:
Note que dados uijt, el problema (6)-(10) puede ser fácilmente resuelto utilizando algún algoritmo que aproveche la estructura en red del problema de flujo. La solución del problema (6)-(10) puede o no, proporcionar soluciones factibles para el problema original (1)-(5). Puesto que el problema lagranjeano resultante (6)-(10) es un problema de flujo de costo máximo en una red extendida de espacio-tiempo, este posee la propiedad de integralidad. Esto implica que la mejor cota superior producido por el problema lagranjeano (6)-(10) para el problema (1)-(5) no es mejor que la cota superior obtenida por la relajación lineal del problema original. Considerando que se quiere encontrar valores para los multiplicadores lagranjeanos que minimicen la cota superior, el problema dual lagranjeano corresponde a:
Para resolver el problema dual lagranjeano, se utiliza el método de optimización de subgradiente, el cual se presenta a continuación como descrito en [13]:
Haga
(cota inferior) igual a 0. Sea ITMAX el número máximo de iteraciones e haga 
como valores iniciales para los multiplicadores.Resuelva el problema lagranjeano (6)-(10) con el conjunto de multiplicadores actual, obteniendo la solución [X,Y] e valor
. Actualice la mejor cota superior min con Haga it= it+1.Teste de factibilidad: si la solución lagranjeana es factible para el problema original, entonces actualice
la cota inferior para el problema correspondiente a una solución factible. actualice la mejor cota inferior 
con 
Teste de optimalidad: pare si(
)<ε; caso contrario, diríjase al Paso 5.Calcule los subgradientes:
Defina el tamaño del paso 𝑡 por:
Donde 0< f ≤ 2 , y actualice los multiplicadores lagranjeanos por:
1. Si it=ITMAX, pare; caso contrario, diríjase al Paso 2.
3.2. Decomposición de Dantzig-Wolfe
En esta sección se presenta la descomposición de Dantzig-Wolfe y el método de generación de columnas. Iniciando con la decomposición, observe que las restricciones de flujo (2) y restricción de movimiento (4) pueden ser agrupadas de acuerdo a cada tipo de vehículo. De esta manera, tomando las restricciones de atendimiento a la demanda (3) como restricciones de acoplamiento, las demás pueden ser agrupadas en conjuntos Xv para todo vЄV, dados por:
El dominio de las variables de los conjuntos Xv puede ser relajado dado que el problema posee la propiedad de integralidad. Así pues, se obtiene la siguiente formulación equivalente a la relajación lineal de (1)-(5)
Por el Teorema de la Representación [14], cualquier solución(xv,yv)Є Xv puede ser descrita como una combinación de puntos extremos y rayos extremos de Xv, dada por:
Donde 
denotan los puntos y rayos extremos de X
v
, respectivamente. En el caso del PAV, los conjuntos son acotados y por lo tanto los rayos extremos no son considerados. Substituyendo esa representación de puntos en el problema encima, se obtiene el Problema Maestro (PM):
Donde λ
v
q
representan las variables del PM, 
representan las columnas del PM, u
ijt
y w
v
representan las variables duales de las restricciones de acoplamiento y convexidad, respectivamente. Para obtener las columnas del PM, se puede resolver los subproblemas siguientes, que determinan un programa de asignación de vehículos cargados y vacíos para cada vehículo tipo v Є V:
De esta forma, el costo relativo de cada variable (columna) λv q es dado por(Zsp -wv). Esto permite inicializar el PM con apenas un subconjunto de columnas, resultando el PM restricto (PMR) y, iterativamente, generar nuevas columnas por medio de las soluciones duales obtenidas del PMR. Ese procedimiento es conocido como el método de generación de columnas (GC), el cual converge para una solución óptima del PM.
Tanto en la relajación lagranjeana como en la decomposición de Dantzig-Wolfe, dado que cada vehículo representa un tipo de vehículo, cada subproblema se vuelve un problema de camino máximo sobre un grafo direccionado de espacio-tiempo, y por ende, se utiliza un algoritmo de camino máximo para grafos direccionados acíclicos [12].
La generación de columnas estándar, basada en soluciones duales optimas, presenta varios inconvenientes, especialmente cuando el método simplex es utilizado para resolver el PMR [15,16]. Entre estos, se encuentran: convergencia lenta próximo a la solución óptima (tailing-off effect); primeras iteraciones con columnas y valores duales irrelevantes (heading-in effect); degeneración del problema dual causa variaciones extremas en el valor optimo del PMR (Plateau Effect); y inestabilidad en las soluciones duales, que salta de un valor extremo a otro (yoyo effect). Así pues, para evitar el efecto negativo de tales inconvenientes, en este trabajo se utiliza la generación de columnas primal-dual [17], una variante del método GC que utiliza el algoritmo de puntos interiores para obtener soluciones duales estables y centralizadas en la región factible del PMR. Mas detalles de estos métodos aplicados al PAV, pueden ser encontrados en [18].
4. Resultados
En esta sección son presentados experimentos computacionales utilizando los métodos de solución propuestos en la sección anterior. Los modelos y algoritmos de este trabajo fueron implementados usando el lenguaje C++/CPLEX 12.6.1 en una maquina Intel® Core ™ i7-4500U, 3,4 GHz y 16 GB de RAM.
Inicialmente fueron tomados 6 ejemplares de 15 terminales, 15 periodos de tiempo y 15 tipos de vehículos, para testar la viabilidad de los métodos en problemas mayores. La Tabla 4 muestra los resultados referentes al subgradiente de optimización. Las columnas se refieren a: nombre del problema (Prob); número de iteraciones de la ejecución (No. Iter.); valor óptimo del problema (Sol. Ot); valor óptimo de la relajación lineal (Sol. Ot. LP); cota superior obtenida con el subgradiente de optimización (C.S); número de la iteración en que la cota de la relajación lagranjeana alcanza la cota de la relajación lineal (Iter); tiempo de ejecución de las 5000 iteraciones, en segundos (CPU LR (seg)); porcentaje de desviación entre la cota superior y la solución óptima de la relajación lineal (GAP LP (%)).
La Tabla 5 muestra los resultados referentes a la GC primal-dual. Las primeras tres columnas son iguales a la Tabla 4, y las restantes se refieren a: cota superior obtenida con la GC primal-dual (C.S); cota inferior obtenida con la GC primal-dual (C.I); porcentaje de desviación entre las cotas de la GC primal-dual (GAP C.S.I (%)); tiempo de ejecución de la GC primal-dual, en segundos (CPU PDCGM (seg)); total de iteraciones de la GC primal-dual (No. Iter).
Se puede observar en la Tabla 4, que el método subgradiente requiere un tiempo computacional excesivo, como consecuencia de los problemas de convergencia, para cerrar el intervalo entre la cota superior y la solución de la relajación lineal en instancias consideradas de pequeño porte. Asimismo, se puede observar en la Tabla 5, que el método GC primal-dual obtiene tiempos computacionales bastante favorables para cerrar ese mismo intervalo. Dadas las observaciones anteriores, el siguiente conjunto de instancias, que se consideran de gran porte, serán testadas únicamente con el método GC primal-dual. Las 30 instancias realistas fueron tomadas del trabajo de [8], las cuales poseen las siguientes características: 53 terminales, 36 periodos - cada periodo de 4 horas; 300 cargas para transportar; y flota heterogénea con 130 vehículos - inicialmente agrupados en 17 tipos de vehículos. Utilizando las formulaciones (1)-(5), esos ejemplares involucran millones de variables y restricciones.
Las Tablas 6 y 7 muestran los resultados de las cotas obtenidas por la GC primal-dual para las instancias realistas. Las columnas de la tabla se refieren a: nombre del problema (Prob); valor óptimo de la relajación lineal (Sol. Ot. LP); tiempo de ejecución para resolver la relajación lineal del problema usando CPLEX, en segundos (CPU LP (seg)); valor óptimo del problema (Sol. Ot); tiempo de ejecución para resolver el problema usando CPLEX, en segundos (CPU IP (seg)); cota superior obtenida con la GC primal-dual (C.S); cota inferior obtenida con la GC primal-dual (C.I); tiempo de ejecución de la GC primal-dual, en segundos (CPU PDCGM (seg)); y total de iteraciones de la GC primal-dual (Iter PDCGM).
De los valores media, mínimo y máximo de la Tabla 6, se puede observar que los tiempos de ejecución de la GC primal-dual son menores que los tiempos de ejecución de CPLEX para la relajación lineal. Desde el punto de vista administrativo, para mejorar los procesos de planeación y control, es deseable gestionar cada vehículo individualmente. De esta forma, cada vehículo es tratado como un único tipo de vehículo. A continuación se muestra los resultados para el caso en que cada vehículo representa un único tipo de vehículo, o sea, la flota es totalmente desagregada.
Cabe resaltar que el caso de 17 tipos de vehículos involucra millones variables y restricciones, y el caso de 130 tipos de vehículos involucran decenas de millones de variables y restricciones, lo que supone modelos de gran tamaño para resolver con softwares de propósito general.
Se puede observar en la Tabla 7 que, aunque el tamaño del modelo de la formulación clásica crece (ya que el número de vehículos fue incrementado de 17 a 130) y por ende el tiempo de ejecución de CPLEX es mayor, el tiempo de ejecución y total de iteraciones de la GC primal-dual disminuye y es significativamente menor que el tiempo de CPLEX. La proximidad de la relajación lineal con la solución óptima del problema y la eficiencia de este método para proporcionar cotas de forma eficiente, muestra un gran potencial de la GC primal-dual para resolver el PAV.
Como último experimento, fue generado un ejemplar de 63 terminales, 36 periodos y 130 tipos de vehículos. Esta instancia fue generada con el propósito de simular el tamaño actual de la red de terminales de la empresa, el cual ha crecido desde que fue elaborado el trabajo de [9,10]. El modelo generado contiene decenas de millones de variables y restricciones. Contrario al software CPLEX, que reporto problemas de memoria para compilar el problema, la GC primal-dual obtuvo el valor óptimo de la relajación lineal en 13 iteraciones y 33 segundos, de los cuales 81% fueron destinados a resolver los Problemas Maestros. Nuevamente, este resultado muestra un gran potencial para tratar problemas de gran porte que no pueden ser resueltos con softwares de propósito general.
5. Conclusiones
El Problema de Asignación de Vehículos (PAV) es de gran aplicabilidad en sistemas logísticos, específicamente en operaciones de transporte de carga por carretera. Dado que ejemplares de gran porte presentan limitaciones para ser resueltos con software de propósito general, heurísticas sin certificado de calidad son utilizadas para resolver estos ejemplares [10]. De esta forma, el objetivo de este trabajo fue estudiar dos métodos que utilizan decomposiciones para proporcionar cotas superiores, y posiblemente inferiores, para instancias de gran porte. El primer método investigado fue relajación lagranjeana, utilizando el método de optimización de subgradiente para resolver el problema dual. El segundo método está basado en la decomposición de Dantzig-Wolfe para resolver la relajación lineal del problema original. Ambos métodos pueden ser insertados en un árbol de busca para encontrar la solución óptima del problema.
Ambos métodos fueron testados inicialmente en instancias pequeñas. Sin embargo, ya que la relajación lagranjeana muestra resultados poco favorables en estas instancias pequeñas, solo la GC primal-dual fue utilizada para resolver instancias mayores. Los resultados se muestran promisorios en términos de eficiencia de tiempo computacional, y dada la proximidad de la relajación lineal con la solución óptima del problema, los resultados también se muestran promisorios para utilizar un método que permita obtener soluciones factibles de buena calidad.
Así pues, los siguientes pasos para una investigación futura consisten en: 1) investigar formas de mejorar las convergencia del método subgradiente e investigar heurísticas lagranjeanas para obtener soluciones factibles del problema original; 2) investigar una MIP-heurística de factibilización para obtener soluciones factibles partiendo de las soluciones del PMR óptimo de la relajación de problema; y 3) colocar la GC primal-dual en un árbol de búsqueda Branch-and-Price para encontrar soluciones óptimas del problema.
