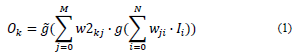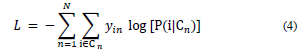1. Introduction
The transportation planning sector needs to model travel mode choice to predict travel demand and understand the causal variables [1]. Currently, the literature shows evidence that travel mode choice depends on a large number of variables including individual, household and exogenous factors like security and comfort on a trip, weather conditions and built environment [2-9].
Different models of travel mode choice, such as discrete choice models, where the travel modes signify mutually exclusive and joint alternatives, have been used within diverse frameworks [10]. The multinomial logit model (MNL) is the most commonly-used discrete choice model for modeling travel mode choice [11,12]. It considers the principle of utility maximization and has a singular mathematical framework which allows for parameter estimation, and so it has been widely adopted in transportation planning [6,13].
However, the MNL model has several limitations because it assumes that the probability of each alternative is independent of the features of the rest of the alternatives [13,14].
Machine learning (ML) algorithms have been demonstrated to work well for statistical approaches used to model travel mode choice. ML algorithms do not make drastic assumptions about the studied data, but learn to represent non-lineal and, in general, complex relationships in a data-driven way [15].
The usefulness of ML algorithms has been demonstrated for many different fields, including transportation planning. In this field, ML algorithms have been used for classifying accidents and studying safety and human behavior, among other applications [16-23].
This paper is organized thusly: First, it presents different machine learning algorithms used in transportation research. Section 2 outlines the most common machine learning algorithms used for transportation research. Section 3 details the most common discrete choice model used for modeling travel mode choice: the Multinomial Logit Model. Section 4 presents a comprehensive comparison of different ML algorithms used for modeling travel mode choice. Section 5 puts forward a discussion and the notable conclusions. Finally, Section 6 lists the references used to construct this review paper.
2. Machine learning (ML) algorithms for transportation research
The expression Machine learning (ML) is used to define a group of methods or algorithms that allow computers to mechanize data-driven model programming and build models by means of a methodical detection of patterns in statistically significant data [24]. In the 1930s, Thomas Ross made the first attempt to develop a machine that simulated the behavior of a living being [25]. Later, Samuel (1959) defined ML as a “field of study that gives computers the ability to learn without being explicitly programmed” [26].
The application of different ML techniques in the field of transportation intends to meet the challenges of growing travel demands, safety concerns, energy consumption, emissions, and environmental degradation [27].
ML algorithms can be classified as follows [28]:
Supervised learning, where ML algorithms generate a function that charts input data to target output data.
Unsupervised learning, where there is no target output data and the ML algorithm simply models a set of input data, looking for clustering in that data [29].
Semi-supervised learning is a combination of both of the above, where ML algorithms use labeled data and unlabeled data.
Reinforcement learning, where ML algorithms learn through their interaction in an environment. The ML algorithm obtains feedback about the accuracy of its response.
Inductive learning is when the ML algorithms learn, based on previous knowledge, their own inductive bias.
In order to build an optimal predictive model, it is vital to consider the following specific phases [27]:
i. Design and data ingestion
This phase includes three steps: data preparation, exploratory analysis and feature extraction. In the first phase, data sources have to be assessed and used to incorporate the advance model into the problem to be solved. This phase is essential because it entails the initial evaluation of the data.
ii. Proof of concept
This second phase includes two steps: modeling algorithms and model evaluation. In this phase it is necessary to choose the model that best fits the data. It is important to take into account the basic differences of every model to achieve a good validation.
iii. Integrate and scale
This final phase includes two steps: initial pilot and full-scale implementation.
This phase represents real-time prediction information about the model’s performance. In this last phase, the model must be continuously updated and adjusted to obtain the best results.
Below, the most popular Machine Learning techniques used in transportation research will be presented. However, it is important to note that there are other algorithms that are not so popular in this field that are not included here.
2.1. Artificial neural networks (ANN)
ANNs are used to extract complex patterns from the data, and perceive trends that are too complex to be observed by humans or other computer methods with their outstanding ability to derive meaning from data that is complex or inaccurate [30-32]. McCulloch and Pitts (1943) introduced the concept of ANN, and it was designed to simulate the functions and structure of the nervous systems in living beings [33].
ANNs are very powerful tools that have been used for numerous applications such as medicine [34-37], transportation [23,38-41], optimization [31,42-45], and even quantum physics [46-50] among others.
ANNs are composed of a large number of neurons, elements that are interconnected in parallel and work in unison to solve diverse problems.
The ANN is trained using input and target data. This process means that available target data is compared with output data provided by the ANN, and later, the ANN’s parameters are adjusted by means of an iterative process until an optimal agreement between reality and the model is accomplished [31].
An example of the structure of an ANN is presented in Fig. 1, where the hidden layer (the first), has a determined number of neurons that need to be defined.
The output layer (the second) has one neuron that is defined with a linear transfer function.
Eq. (1) presents the formulation of an ANN:
In Eq. (1):
O k : ANN output.
M: quantity of “output” elements.
I i : “input” data.
N: quantity of input attributes.
w ji : synaptic weight of the first layer.
w2 kj : synaptic weight of the second layer.
Synaptic weight w ji describes the strength of a synaptic connection between the postsynaptic neuron i and the presynaptic neuron j. This structure is capable of recognizing non-linear relationships between input data and output data [32].
Other advantages of ANNs include [32,51,52]:
Its adaptive learning: The skill to use the data given during training to learn how to do specific tasks.
Its self-organization ability: A big advantage of ANNs is that they arrange their own information obtained during the learning process.
Its real time operation: Another advantage is that computations of ANNs can be accomplished in parallel and special hardware devices have been designed which take advantage of this special skill.
Its failure tolerance by means of redundant information coding: fractional destruction of an ANN leads to degradation of the performance.
There are different types of ANN, the most well-known are:
2.1.1. Self-Organizing Maps (SOM)
Self-Organizing Maps (SOM) are unsupervised ANN that reduce the input dimensionality with the aim of representing distribution as a “map”, where similar points are mapped carefully together [53].
SOMs are very useful for visualization due to the way they take high-dimensional data and create low-dimensional images of it.
It is possible to perform cluster analysis on the map itself, because it has thousands of nodes.
2.1.2. Convolutional Neural Networks (CNN)
CNN are commonly used for image processing applications. Energy, computational mechanics, electronic systems and remote sensing use CNN for analysis and prediction among other applications.
In other words, CNNs are regularized versions of fully connected networks, which means that each neuron in one layer is connected to all neurons in the next layer [54].
2.1.3. Recurrent Neural Networks (RNN)
RNN are Artificial Neural Networks that contain cyclic connections, making them a more powerful tool for modeling sequence data than standard ANN. This technique has proved to be an outstanding success in sequence labeling, speech recognition, language modeling and handwriting recognition [55].
It is important to briefly mention that the ANN algorithms detailed above are related to Deep Learning. Deep Learning is a term introduced by Ian Goodfellow et al. in 2016 [56], for “a form of machine learning that enables computers to learn from experience and understand the world in terms of a hierarchy of concepts, because the computer gathers knowledge from experience, there is no need for a human computer operator to formally specify all the knowledge that the computer needs. The hierarchy of concepts allows the computer to learn complicated concepts by building them out of simpler ones; a graph of these hierarchies would be many layers deep.”
Deep learning algorithms have recently emerged from ML techniques, and these methods exploit much deeper and more complex architectures than ML algorithms, and can achieve better results than traditional methods in many fields [57].
2.2. Decision Trees
Decision trees (DTs) are oriented graphs formed by a finite number of nodes departing from the root nodes [58].
Decision trees are non-parametric methods with a similar structure to a flowchart or to a tree and they can be used to classify problems [24].
Decision trees are powerful algorithms for classifying data, where a tree structure is used for modeling the different relationships between the features and potential output data. This ML algorithm is so-called because it simulates a real tree, which begins at a wide trunk, and as it rises is divided into narrower branches. Similarly, DT use an architecture of branching choices, beginning with the main question for a specific problem which needs to be answered to solve that problem, later a secondary question must to be answered to continue disaggregating the data and classifying outcomes.
For a better understanding of how a DT works, consider the decision tree presented in Fig. 2, which predicts if it is a good idea to make a trip by bike from an origin to a destination. The bike trip to be considered starts at the origin node, where it is then passed through different decision nodes that need to be assessed, considering the characteristics of external conditions (rain, travel time or topography). These assessments divide the data into different branches that indicate probable outcomes of a decision, represented as Yes or No results. It is possible for these decisions to have more than two alternatives.
When a final decision is made, the DT ends with leaf (or terminal) nodes denoting the action to be taken as the final result of the series of choices.
A great advantage of DT is that the flowchart-like tree structure is not exclusively for internal use. When a DT algorithm is built, it is easily interpreted by those without technical knowledge.
This feature means that a model can be assessed as to whether it works well enough for a specific task.
In addition to this, DTs can be interpreted easily, and they can deal with non-linear relationships and interactions between every variable. However, DTs are very sensitive to noisy data, and also tend to overfit the data, rendering it useless [59]. Tree-based algorithms combine various DTs in order to build more accurate and steady classifiers than simple DTs [60].
To summarize, some advantages of DTs are:
Their functioning is easy to understand and interpret.
They require little data preparation from the user to build an optimal DT. There is no need to apply normalization to the data.
On the other hand, the main disadvantage of DT is that they have a great probability of overfitting noisy and defective data, and this probability increases as the tree gets deeper and more complex.
Some potential uses of DT algorithms include:
Diagnosis of medical conditions based on symptoms or laboratory measurements in medicine.
Credit scoring models for banking agencies.
Marketing studies of customer behavior for advertising agencies.
Modeling travel mode choice, as will be seen later in this paper.
In general, DT algorithms are one of the most-used ML techniques, and they can be applied to model many types of data [61].
Bagging is a straight-forward tree-based algorithm method, whence several DTs are trained at the same time in parallel using bootstrap samples of the data. Class assignments for the final prediction are determined by the majority vote of all trees running in parallel [62].
Random forests (RFs) are other tree-based algorithms that are associated with bagging. While RFs train several decision trees in parallel using bootstrap samples of the data, each split at the nodes of the trees is calculated by a random subdivision of features. Like bagging, RFs determine class assignment for predictions through the majority vote of the ensemble of trees [63].
2.3. Support-Vector Machines
Support Vector Machines (SVMs) are another ML algorithm method used for binary classification. SVMs can be defined as risk-based supervised learning algorithms for classifying data patterns by identifying a frontier with a maximum margin within data of the same class [24,64].
SVMs are considered to be supervised learning algorithms; when they are given labeled training data, the SVM outputs an optimum flat boundary called a hyperplane. The hyperplane is simply a line splitting a plane into two portions in a two-dimensional space, where each class lies either side of the line.
An SVM algorithm classifies data by projecting the target variables into a high-dimensional feature space, where classes are linearly separable [65]. It is possible to imagine an SVM as a surface that generates a limit between datapoints plotted multidimensionally, representing samples and their respective attribute values.
An SVM, in order to perform linear classification, overcomes a non-linear classification, indirectly plotting its inputs in high-dimensional feature spaces.
If data is unlabeled, is not possible to use a supervised learning algorithm, and an unsupervised learning method is required, which tries to discover natural groupings of data to assemble and then plot new data to the ensembles formed. There are SVM algorithms that use the statistics of Support Vectors to classify unlabeled data. They are called Support Vector Clustering [66].
Support-Vector Machines can be adapted for use with almost any type of learning task, including prediction and classification. Many of the algorithm’s key successes have been in pattern recognition of data. Prominent applications include [61]:
Text categorization to identify the language used in texts.
Detection of events like earthquakes or security breaches.
Discovery of uncommon and important events, like combustion engine failure.
Classification of microarray gene expression data, for identifying cancer and other important diseases.
Classification of texts by subject.
Modeling travel mode choice, as will be seen later in this paper.
2.4. Cluster Analysis
Cluster Analysis (CA) is an unsupervised machine learning technique used to divide the data into similar groups with similar features, with the aim of maximizing the heterogeneity between clusters (groups) and the similarities between in-cluster samples [67,68].
It divides data into separated clusters without first having been told how the clusters should look. As it is an unsupervised ML algorithm, CA is issued for knowledge detection rather than prediction. It offers an insight into the natural grouping of the data.
Latent Class Clustering (LCC) is a particular method with advantages over regular CA, similar to Ward’s method and k-means. These advantages include access to much statistical criteria used for deciding the suitable number of clusters, and the ability to use different types of features with no need for previous standardization which could modify the outcomes [69].
The relevance of CA lies in that the clusters can then be used for action. For example, CA are employed to [61]:
Perceive anomalous behavior, such as unauthorized network intrusions, by recognizing different patterns of use that fall outside the known groups.
Divide customers into clusters with similar socioeconomic aspects or buying patterns for advertising campaigns.
Simplify large datasets by clustering features with similar values into a smaller number of homogeneous categories.
CA is useful whenever differences in the data can be exemplified by a small number of clusters. CA reduces complexity and give insight into patterns of relationships.
The k-means clustering algorithm is the most popular CA algorithm and serves as the foundation for many sophisticated clustering techniques. It is popular because it uses simple principles which can be described without using statistical concepts. K-means is highly flexible and can be modified using simple changes to overcome all of its shortcomings and so achieve optimal results in several real-world cases.
On the other hand, the main weaknesses of k-means lie in that it is not as sophisticated as modern cluster techniques because it uses a component of random chance, and that it will find the best set of groups is not guaranteed. The other disadvantage is that it relies on estimation to assign the number of groups for the data [61].
CA algorithms (including k-means) have been used in different fields of transportation engineering with optimal outcomes [70-74]. Some authors [7,75] used LCC analysis to segment heterogeneous traffic accident data sets into homogenous accident. De Oña et al. [58] used a CA method to assess passenger heterogeneity, where the CA method stratified the sample of passengers into clusters with similar features and therefore into clusters of homogeneous perceptions concerning the service. Other authors [76] used a CA to analyze the effect of workplace relocation on an individual’s travel behavior and activity.
3. Multinomial Logit Models for modeling travel mode choice
Multinomial Logit Models (MNL), and a large number of variations on them, are extensively used for modeling travel mode choice [11,14,77-79].
The existence of an individual n and a set of m variables X n = {X 1n , ..., X mn } can define a choice set C n of I alternatives and corresponding utility functions (Eq. 2 and Eq. 3):
Where:
ε 1n , ..., ε mn are independent and identically distributed random variables (iid). In other words, if all variables have the same probability distribution, and every variable is mutually independent of each other, it is said that the sequence of variables is iid.
β 1 , …, β m is the set of parameters to be estimated. This is carried out by means of a minimization of the negative log-likelihood (the logarithm of the likelihood function, the function that estimates a parameter from a set of statistics) (Eq. 4):
where y in = 1 if individual n chooses i. Otherwise, y i = 0. The probability of choosing i ∈ C n for MNL is presented in Eq. (5):
This mathematical model has deep theoretical foundations [10] making widespread use of ε to express statistical properties.
One important disadvantage of these type of models compared to ML techniques is that a Logit model typically focuses on parameter estimation and does not lend enough importance to prediction. On the other hand, one big advantage of Logit models compared to ML algorithms lies in that ML algorithms are built for predicting values, but are frequently considered to be difficult to infer and are almost never used to extract behavioral findings from the model outputs [80].
4. Machine Learning (ML) algorithms for modeling travel mode choice
Several ML algorithms have been used for modeling travel mode choice in recent decades. This paper will cover the most important ones.
Regarding ANNs, Shmueli et al. (1996) [81] compared a simple Multilayer Perceptron (MLP) to non-linear classification and regression trees. After this comparison they demonstrated that both methodologies perform similarly, and they perform optimally when modeling travel mode choice.
Later, Sayed and Razavi (2000) [82] used fuzzy artificial neural networks, demonstrating that they can be used to classify in the same way that Probit and Logit models are usually used to model travel mode choice.
Mohammadian and Miller (2002) [83] compared the performance of MLP and Nested logit models, showing that the first has a significant advantage over the second when the percentage of properly classified instances for predicting domestic vehicle choices are considered.
Vythoulkas et al. (2003) [84] showed that outcomes from fuzzy artificial neural networks that model travel mode choice compare positively to a Logit model.
Cantarella and De Luca (2003) [38] trained two ANNs with different frameworks to model travel mode choice. They showed that both artificial neural networks perform better than a Multinomial Logit model.
Other authors, like Hensher and Ton (2000) [85], Xie et al. (2003) [86], Andrade et al. (2006) [87], Celikoglu (2006) [39] and Zhang and Xie (2008) [88] demonstrated that the predictive capability of MLP is superior to multinomial and nested logit models, concluding that MLP could overcome the utility function estimation in the modeling of travel mode choice.
Zhao et al. (2010) [40] have shown that the precision of probabilistic artificial neural networks is comparable to basic artificial neural networks for predicting travel mode choice, while Omrani et al. (2013) [41] posited that ANNs are more precise than the other alternatives that they examined.
Pulugurta et al. (2013) [89] found that fuzzy ANN were better for detecting and including human knowledge and cognitive activities into mode choice behavior.
On the other hand, there are some publications that come to the opposite conclusion, like Abdelwahab and Abdel-Aty (2002) [20] who proved that a two-level nested logit model beats the Multi-Layer Perceptron (ANN) in the analysis of driver injury severity, or Teng and Qi (2003) [90, 91] who presented the supremacy of wavelets over diverse artificial neural network frameworks for modeling incident detection.
Decision trees (DTs) have also been applied for modeling travel mode choice. For example, Xie et al. (2003) [86] compared DTs and ANNs with MNL models, concluding that DTs and ANNs outperform MNL models. Additionally, they found that DTs are more effective and can be better interpreted than Artificial Neural Networks.
On the other hand, Rasouli et al. (2014) [92] explored the connection between predictive performance and the number of decision trees by means of ensemble learning. Results of this study suggest that the accuracy of predicting transport mode choice is improved, although non-monotonically, with increasing ensemble size.
Tang et al. (2015) [93] used DTs to explore travel mode choice in cases in which individuals have only two options to choose between, looking to understand people’s mode-switching behavior. In this paper it was demonstrated that DT outperforms MNL models in predictive capability.
Zhan et al. (2016) [94] used hierarchical tree-based models for exploring the travel characteristics of students from China, determining which variables influenced their travel mode choice.
Ravi Sekhar et al. (2016) [95] used a random forest DT to model travel mode choice in Delhi, by means of 5000 stratified household samples collected in the city using household interview surveys.
Hagenauer and Helbich (2017) [62] proved that a decision tree framework, specifically a random forest algorithm, outperforms any of the other classifiers that were investigated, even an MNL model.
Cheng et al. (2019) [96] applied a random forest algorithm to model travel mode choice behavior, obtaining outstanding results.
SVM algorithms have also been used to model travel mode choice, for instance, Zhang and Xie (2008) [88] compared Support-Vector Machines, Artificial Neural Networks and Multinomial Logit models for modeling travel mode choice and demonstrated that Support-Vector Machines provided the highest accuracy of every tested model. On the contrary, Omrani (2015) [97] demonstrated that Artificial Neural Networks have a higher accuracy than Support-Vector Machines and Multinomial Logit models for predicting the travel mode of individuals in the city of Luxembourg.
Additionally, Xian-Yu (2011) [98] demonstrated that an SVM model has fast convergence and high precision, outperforming ANN and nested logit models, which is a very important consideration for modeling travel mode choice.
Regarding CA, Ding and Zhang (2016) [99] estimated travel behaviors by dividing individual travelers into several groups based on their personal features using CA.
Li et al. (2016) [100] implemented a cluster-based logistic-regression model to predict travel mode choice during holidays in Beijing, where they employed a regression and a DT method to split the source data into groups, and they concluded that since the cluster-based logistic regression model evades the variable interaction effects, it outperforms the logistic-regression model in its prediction accuracy.
Also, in 2016, Pirra and Diana [101] used CA to socioeconomically characterize different profiles of travelers in the U.S. with specific kinds of tours.
On the other hand, Molin et al. (2016) [102] conducted a latent class cluster analysis to identify multimodal travel groups based on the self-reported incidence of mode use, finding that most car drivers have negative attitudes towards bicycles and public transport, while car drivers who often use public transport have more positive attitudes to bicycles and public transport.
The above-mentioned publications are exhaustive contributions to applications of ML methodologies for modeling travel mode choice, however, although there are a huge number of Machine Learning classifiers available, these investigations only deal with a limited set of these [103]. Along these lines, Hagenauer and Helbich (2017) [62] carried out a comparative study of seven ML classifiers for modeling travel mode choice (included the commonly used MNL), showing that an advanced classifier like the random forest significantly outperforms all the other investigated classifiers. Regarding this assumption, Fernández-Delgado et al. (2014) [103] have proven that random forests can produce highly accurate outcomes for many applications.
Table 1 presents different approaches used by the authors mentioned here to model travel mode choice using Machine Learning algorithms.
Table 1. Analysis of literature on modeling travel mode choice.

1: CLA: Classification, FA: Function Approximation.
2: RF: Random Forests, SVM: Support Vector Machines, F: Fuzzy, RBF: Radial Basis Function, MLP: Multi-Layer Perceptron.
3: BP: Back-Propagation, LM: Levenberg-Marquardt.
Source: The Author.
5. Discussion and conclusions
With the increasing popularity of ML algorithms in transportation research, there are many questions related to their advantages and disadvantages when compared to the Logit models that are commonly used to model travel mode choice. For this reason, this paper presents a comparison of these methodologies.
When compared to different ML algorithms that model travel mode choice, ANNs, DTs, SVMs and CA algorithms perform exceptionally well, better than MNL for almost every case. In addition, if multiple Decision Trees are combined in a Random Forest algorithm, its outcomes are better than any other machine learning algorithm.
The better performance of Random Forest can be attributed to its flexibility and power combined into a single ML method. As ensemble use is just a minor, random portion of the full feature set, RF approaches can handle enormous datasets, where other models might fail. At the same time, error rates for the majority of learning tasks are similar to any other approach.
ANN models have been applied in countless research projects for modeling travel choice mode, but in many cases, researchers implement this algorithm blindly, disregarding some of its inadequacies such as its intrinsic inability to present an exclusive solution to an issue (for this reason, it is common for many researchers to refer to ANN models as “black-box models”) [107].
For many authors, the lowest accuracy was given by the MNL model, demonstrating its less effective modeling abilities for modeling travel mode choice.
There is great potential in the integration of ideas from Logit and ML algorithms (and the exploration of ideas from Deep Learning techniques as well) to develop sophisticated models for modeling travel mode choice and proposing some possible research avenues, like, for example:
Exploring which ML technique is most suitable for modeling travel mode choice.
Incorporating the behavioral assumption that considers alternative-specific, which is enabled by the data framework of logit models “layered” into ML techniques.
Exploring Deep Learning techniques for modeling travel mode choice.