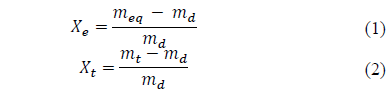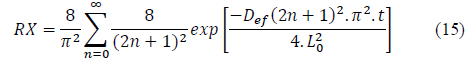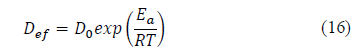1. Introduction
Punamuña leaves (Satureja boliviana) grow up in Peruvian Andean ecosystems and it is considered and important germplasm of wild life; this has healing properties reported by traditional medicine and ethnobotany [1]. This wild plant has popular names like Cjuñuca, Cjuñu muña, Orégano de los Incas, Martín-muña [1,2].
The currently demand of aromatic native herbs with minimal transformation like the drying process are trends in national and international markets [3], the punamuña is not the exception for its medicinal properties [4,32].
Drying process allows to eliminate water to inhibit the growth of harmful microorganisms and some deterioration reactions [5], which reaches using hot air [6]. However, food suffer color changes due to the oxidation of its components [7], affecting its sensorial properties [8].
Drying kinetic enable to know the moisture variation with the time giving an idea about the energy consume, water transfer mechanisms and the influence of the drying parameters like temperature, input humidity and air velocity; which allows to design and select more efficient dryers [9].
Models allow to predict drying process and offer tools to define storage conditions and packaging, this helps to know the final condition in agricultural products [10].
Drying models represent equilibrium conditions between the adsorbent and the adsorbate [11], and is related to the speed of the water molecules that move from the inside to the food surface known as effective diffusivity, due to an energy of initiation or activation energy [5,12,33].
This study aimed to evaluate the drying kinetic, effective diffusivity, activation energy, and the color of the punamuña leaves (Satureja boliviana) at 40, 50 y 60 °C and air velocity of 0.5 and 1.0 m/s.
2. Materials and methods
2.1 Vegetal material
Wild punamuña leaves (Satureja boliviana) were collected in Yunca Alta zone (13° 36 07.89´´ S, 73° 16´ 33.13´´ O, and 3650 m of altitude) in February 2018, from the city of Andahuaylas, Apurimac, Peru.
2.2 Drying process
The drying was carried out in the chemistry laboratory at Jose Maria Arguedas National University in Andahuaylas, Peru. The fresh leaves (50 g) were placed on stainless steel trays (20 x 20 cm) with five repetitions and they were taken to a horizontal forced air dryer at 40, 50 and 60 °C and air velocity of 1.0 and 0.5 m/s.
Sample weight loss was registered at 10 minutes intervals on an electronic scale (Oha Pioneer model, Ohaus).
2.3 Drying kinetics modelling
The equilibrium humidity (in dry basis - d.b.) (X e ) was calculated in relation to the mass of the sample in equilibrium (m eq ) and the dry mass (m d ) (Eq. 1), the water fraction of the product over time (in d.b.) (X t ) was determined in function to the mass of the sample over time (mt) and the dry mass (m d ) (Eq. 2).
The drying curves were constructed by graphing the experimental moisture ratio (RX e ) (Eq. 3) in function to the time [13]. Then, it was adjusted to 10 exponential models (Table 1) through the Quasi-Newton method using the Statistica V8 software [14] taking as convergence criteria values close to 1.0 of the correlation coefficient (R2) and the smallest relative mean error (%E) (Eq. 4).
Where X t water fraction of the product over time (in d.b.), X 0 initial water fraction of the product (in d.b.), and X e water fraction of the product at equilibrium (in d.b.).
Where RX e experimental humidity ratio (in d.b.), RX c humidity ratio calculated from the model (in d.b.), and n number of observations
2.4 Determination of the effective diffusivity
The effective diffusivity coefficient was calculated using Fick’s second law to long times, for n = 0 and n =10 terms (Eq. 15). Regarding; infinite plate, uniform initial moisture content; and constant geometry during drying [15].
Where RX - humidity ratio dimensionless (in d.b.), D ef effective diffusivity coefficient (m2/s), L 0 leave thickness (m), n number of terms in the equation, and t time (s).
Table 1. Exponential models for drying kinetic.

Where: RX - Humidity ratio, dimensionless; a, b, c, k, k0, k1 - model constants; t - Time, min
Source: Adapted from [34].
2.5 Determination of activation energy
The influence of temperature on effective diffusivity was evaluated through the activation energy using Arrhenius’s equation (Eq. 16).
Where D 0 pre-exponential factor m2/s, E a activation energy (kJ/mol), R universal gas constant (8.314 kJ /kmol-K), and T absolute temperature (K).
2.6 Evaluation of color
The color of the punamuña leaves were determined in the CIE space L* a* b*, which are L*, luminosity (0 = black and 100 = white), a* and b*, rectangular color coordinates (+a = red, -a = green, +b = yellow y -b = blue) [16]. It was performed 5 readings using a colorimeter (CR400 model, Konica Minolta). The a*/b* ratio was calculated, as well as the color difference with respect to the fresh leaf (ΔE*) (Eq. 17) [17].
2.7 Statistical analysis
Analysis of variance and Tukey's multiple comparison means test were performed at a significance level of 5%. The data were processed with the statistical package Statistica V8 software [14].
3. Results and discussion
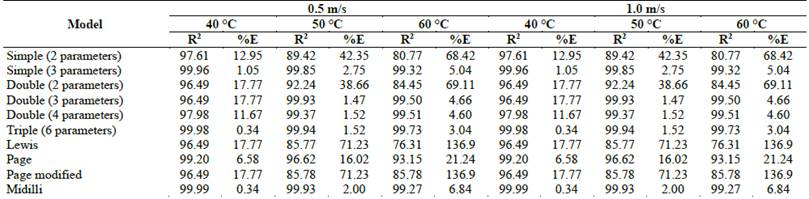
Table 2 shows parameters of the 10 exponential models, which are adjusted to the experimental data for drying punamuña leaves at the study temperatures and air velocities of 0.5 and 1.0 m/s.
It was observed that at 0.5 m / s the parameter k increases with temperature in the study models, except for the model with four parameters and triple with six parameters. On the other hand, at 1.0 m/s the models as double with four parameters, Page and Midilli decreased.
The behavior of parameter b with temperature is random in the models, although it was observed that for the simple exponential model with three parameters it increased, while it decreased for the triple models with six parameters and Page at a drying speed of 0.5 m/s. At 1.0 m / s the behavior is even more random, being characteristic in many foods subjected to drying [9,12].
The c and k parameters increased with the temperature for the triple model with six parameters for both air velocities. This behavior is characteristic in the drying of some food [13,18].
Values of %E < 10.0 and R2 close to the unity are recommended as a criterion for good adjustment of models [19]. The simple exponential model with 3 and 6 parameters and Midilli showed better adjustment (R 2 > 99.9% and %E < 6.84), (Table 3).
The exponential model with six parameters reported better values of R 2 and %E. This model allows to describe the drying kinetic appropriately in different food [18,20] such as reported by Doymaz, [21] in the drying of thyme (Thymus vulgaris) for ranges from 40 to 60 °C at 2 m s-1, Arslan & Ozcan [22] in the drying of alecrim leaves (Rosmarinus officinalis L.) and Radünz et al., [23] in the drying of carqueja (Baccharis trimera) for ranges from 40 to 90 °C.
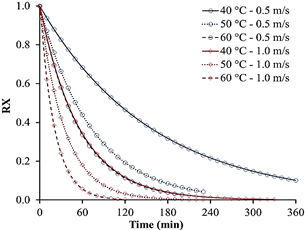
The drying curves graphed using the triple exponential model with 6 parameters are in Fig. 1, which shows that punamuña leaves eliminate higher amount of water with the increase of the temperature and air velocity (steep slope) achieving decrease the drying time.
Source: The Authors.
Figure 1 Drying curves graphed with the triple exponential model with six parameters
The adjusted curves do not present an unstable period although this period is subject to the material to be dried [24], and show a constant period of short duration, according to Doymaz [21], Radünz et al., [23] the elimination of water in this phase is higher and allows to attain the equilibrium humidity or constant weight quickly. Lisboa et al. [18] mention that, this phenomenon is characteristic for materials with small thickness which quickly obtain heat of vaporization, and facilitating the water movement towards the surface [22,25].
Values of effective diffusivity for drying punamuña leaves at 40, 50 and 60 °C and drying air velocities of 0.5 and 1.0 m/s are presented in Table 4. It shows that modeled data using Fick’s equation with n = 0 and n=10 reported values of R 2 > 80.70 which are recommended values of good adjustment R 2 > 70.0 [26]. However, the modeling with n = 10 reported better values of R2.
The effective diffusivity increases from 3.02 x 10-11 to 8.27 x 10-11 m2/s with the increasing temperature for drying at 1.0 m/s while at 0.5 m/s air velocity increased from 1.01 x 10-11 to 2.78 x 10-11 m2/s.
The increasing effective diffusivity is due to the increment of the evaporation rate of water from the food towards the ambient because of the warming effect [25,27]. Effective diffusivity values are similar for dried materials such leaves and flowers [21-23].
On the other hand, the increasing air velocity increases the effective diffusivity considerably. At 40 °C, the effective diffusivity increases from 1.01 x 10-11 to 3.02 x 10-11 m2/s for air velocities from 0.5 to 1.0 m/s respectively. This phenomenon is because of the combined heat and mass transfer effect that occurs in the food, the warming air flow eliminates the water that is on the surface of the food [28], in addition to that Doymaz [21] and Lisboa et al. [18] reports similar behavior as well.
The activation energy for drying punamuña leaves was 43.62 and 44.52 kJ/mol at 1.0 and 0.5 m/s of air velocity respectively (Table 5). This value is characteristic for drying leaves from plants such as Arslan & Ozcan, [22], Doymaz, [21] and Gomes et al. [20] report it.
Activation energy decreases with the increment of air velocity and presents an inverse relation with the effective diffusivity. This means that it is necessary higher energy to remove water from the leaves when the air velocity is low. According to Corrêa et al. [5] the smaller it is activation energy, the effective diffusivity will be higher.
The results for color of the punamuña leaves in terms of L*, a* and b* are in Table 6. These values change significantly with the temperature and air velocity (p-value < 0.05). The luminosity (L*) decrease from 42.36 to 29.69 and 42.36 to 33.01, while a* increases from -11.77 to 0.22 and -11.77 to 0.95, and b* decreases from 21.24 to 8.10 and 21.24 to 10.14 at air velocities of 0.5 and 1.0 m/s respectively.
Table 6 L* a* b* values and color difference (ΔE*) of punamuña leaves

Means values with different letters inside columns are statistically significant at p < 0.05
Source: The Authors.
It is very important to achieve high values of L* or close to the fresh product which depend on the drying conditions. However, the increment of temperature decreases L* values considerably [29] because chemical oxidation reactions are promoted [7].
It does not exist significant difference between L* and the fresh leaf at 40 ºC for both drying air velocities, while a* parameter tends to red and b* to yellow, they present different values from the fresh leaf.
The relation (a*/b*) is a good color indicator and it is recommendable low values [29,30], and it happens at 40 and 50 ºC of drying. It increases considerably when the temperature increases (p-value < 0.05) which shows that sensorial properties of punamuña leaves are being affected [8].
The difference color (ΔE*) can classify in very different when ΔE* > 3, different (1.5 < ΔE* < 3) and minimally different (ΔE* < 1.5) [31]. In all the cases the results indicate that the color of punamuña leaves are completely different from fresh leaf (p-value < 0.05) that is ΔE* > 8.80, which show that they are more affected at low air velocities because they are more exposed to heat due to the longer drying time.
4. Conclusions
The triple model with six parameters presented better adjustment in the drying of the punamuña leaves with a correlation coefficient higher than 99.73% and a relative mean error less than 3.04%, the effective diffusivity coefficient evaluated for 10 terms showed an increasing trend with increasing temperature and drying air velocity, the effect of temperature on the effective diffusivity calculated through the activation energy was 44.52 and 43.62 kJ/mol at air velocities of 0.5 and 1.0 m/s respectively, while the luminosity (L*) decreases considerably with increasing temperature, while at low air velocity the relation a*/b* and ΔE* increases with the temperature and at low drying air velocity is recommended drying conditions less than 50 °C and air velocity of 1.0 m/s.