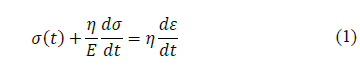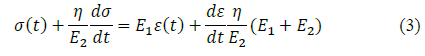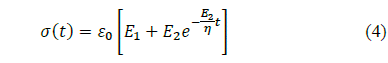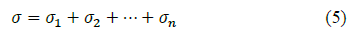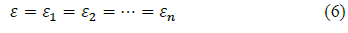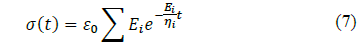1. Introduction
Elastomers time-dependent mechanical properties are caused by their viscoelastic behavior, in which the dual response of an elastic solid and a viscous fluid will determine their properties. Stress relaxation, creep, energy dissipation, hysteresis, strain rate, and loading history dependency are other phenomena inherent to the viscoelastic behavior. During experimental testing, it is preferable to apply step stresses or strains (creep and stress relaxation, respectively) instead of a ramp (in which constant stress or strain rates are applied) because the time effect is isolated from any non-linearity [1]. Furthermore, the properties are related to the dissipated energy due to molecular mobility, break and reformation of the filler transient network, and slippage of rubber molecules under high strain [2]. Understanding these properties plays an important role in the selection of the rubber compounds for different applications subjected to long-term loading.
A fundamental method to describe the viscoelastic time-dependent behavior is the stress relaxation test, in which a sudden constant strain is applied, and the stress required to maintain that strain decreases with time. Moreover, accurate measurement of physical properties is required for their full-scale adoption and integration in industrial settings [3]; therefore, several phenomenological mechanical models have been proposed, and some simple linear models are useful to gain physical understanding of some viscoelastic-related behaviors such as stress relaxation, and to assess the stress-strain relationship of viscoelastic materials [4]. Such models consist of springs and dampers in a variety of arrangements, which represent the elastic and viscous response of viscoelastic materials, respectively. However, that arrangement will determine the capability of the model, that is, models that contain a free damper such as the Kelvin model (a spring and damper connected in parallel) will not allow a sudden increase in strain. For such behavior (i.e., stress relaxation), the Maxwell model (a spring and damper connected in series) is adequate; however, a more realistic behavior relating the stress relaxation process can be modeled by the Zener model (or standard linear solid model) or arranging several Maxwell elements in parallel (Wiechert or generalized Maxwell model) [1]. Fractional derivative models are also capable to model the viscoelastic materials behavior [3].
The generalized Maxwell model has been used to estimate stress relaxation of tensile specimens of EPDM rubber [5] and constituted collagen gels [6]. Bhuiyan et al. [7] assessed the mechanical behavior of rubber bearings subjected to long-term compression, cyclic shear, and their combination, by proposing an elasto-viscoplastic model based on the Maxwell model. Kumar et al. [8] used the Jeffrey model, which contains two non-linear dampers, to model the multistep relaxation response of a natural rubber specimen in tension. Marvalova [9] proposed a phenomenological model to evaluate a carbon black-filled rubber under monotonic, cyclic, and relaxation tests. Xu and Hou [10] developed a theoretical model to analyze stress relaxation curves of several materials such as pure ice, cheese, bovine muscle, PVC, metals, and bone. However, the linear Wiechert model with few Maxwell elements has not been evaluated under stress relaxation in compression of carbon black-filled natural rubber-based compounds. Therefore, this study compares the Maxwell, Zener, and Wiechert linear phenomenological mechanical models to evaluate the viscoelastic behavior of a carbon black-filled natural rubber under stress relaxation, and its calculated parameters are compared to the compressive modulus and a relaxation rate experimentally obtained. The viscoelastic behavior was assessed calculating the model parameters using an optimization algorithm in Python, which includes the curve fitting tool that uses the non-linear least squares to fit the function to the experimental data. The trf (trust region reflective) method, suitable for problems that require bounds, was used since it iteratively solves subproblems by a diagonal quadratic term.
2. Experimental
2.1 Materials
Three natural rubber-based compounds reinforced with 15, 30, and 45 phr (parts per hundred of rubber) of N550 carbon black were studied (hereafter called NR15, NR30, and NR45 respectively). The compounds were obtained in an open two-roll mill using the same ingredients with only the carbon black content varying among them. Cylindrical specimens of 28.6±0.1 mm in diameter and 12.5±0.5 mm in height were obtained according to the recommendations of ASTM D575 [11] standard. Cylinders were vulcanized using a hydraulic press at 160°C at an approximate pressure of 4.6 MPa during 33 min; thus, the rheometric and viscoelastic properties of the materials were evaluated in previous studies of the author [12] obtaining a compressive modulus of 2.43±0.08, 3.55±0.05, and 4.61±0.15 MPa for the NR15, NR30, and NR45 compounds, respectively. Those values were calculated as the initial slope of the third cycle of the stress-strain curve from a uniaxial compressive test at a constant deformation rate of 12 mm/min. Additionally, the compounds evaluated in this study are typically used in laminated rubber bearings applications [12].
2.2 Stress relaxation tests
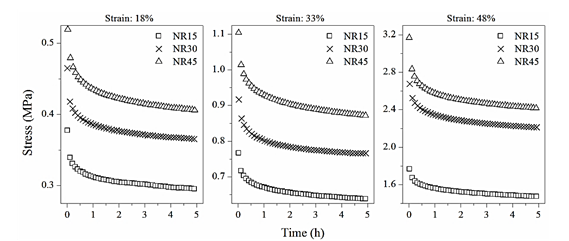
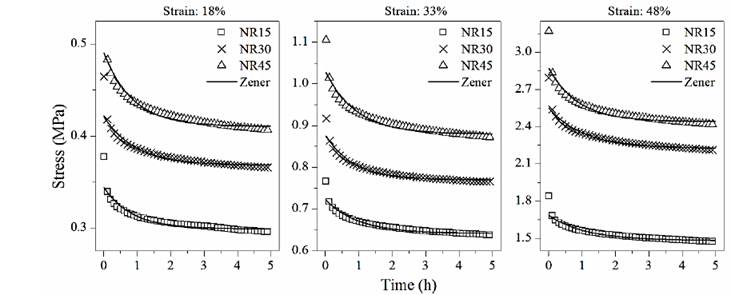
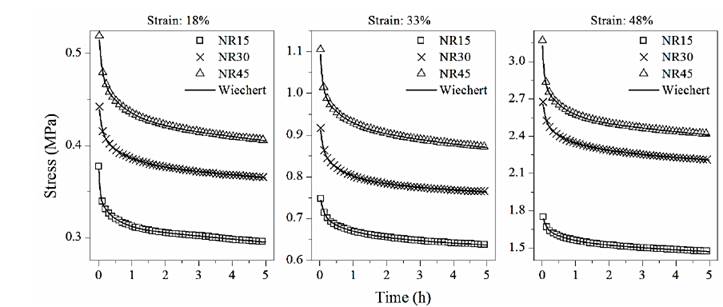
Uniaxial compressive stress relaxation tests were performed to the cylindrical specimens to simulate real conditions of rubber bearing applications. Therefore, restraining slippage conditions were used as in [12], and different strain levels were applied during 5 hours due to restrictions of the testing machine and since no specific time is indicated in ASTM E328 [13] standard. Tests were performed at room temperature using a SHIMADZU AGS series universal testing machine with a 50 kN load cell and a resolution of 0.01 N. Tests were performed at the Polymer Processing Laboratory at Universidad de Antioquia. Fig. 1 shows the stress relaxation curves of the compounds at different strain levels (18, 33, and 48%). Additionally, a relaxation rate was calculated as the percentage of the maximum initial stress through the duration of the test. The relaxation rates were 4.05±0.28, 4.17±0.12, and 4.93±0.31%/hour for the NR15, NR30, and NR45 compounds, respectively.
3. Constitutive model fitting
3.1 Maxwell constitutive model
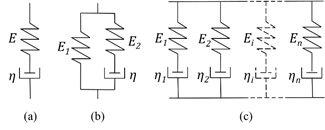
Fig. 2a shows the simple Maxwell constitutive model, which consists of a spring and a damper connected in series. The spring and the damper represent the elastic and viscous response respectively.
The constitutive equation of the Maxwell model is defined as:
where σ is the applied stress, E is the corresponding elastic modulus (linear spring representing the elastic behavior as a Hookean solid), η is the viscosity (linear viscous damper representing the viscous behavior as a Newtonian fluid), and ε the strain. Since the representation of stress relaxation implies that ε(t)=ε 0 is constant (defined experimentally at 18, 33, and 48%), then dε/dt=0 , and the solution for σ(t) of eq. (1) is:
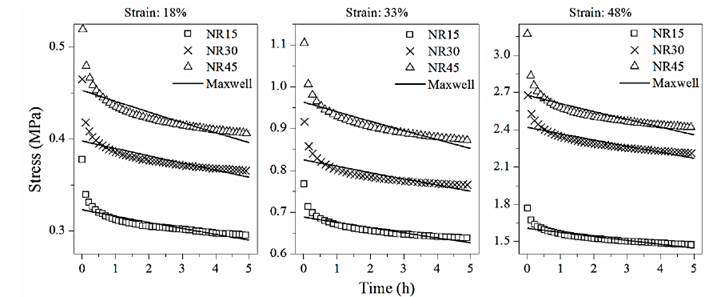
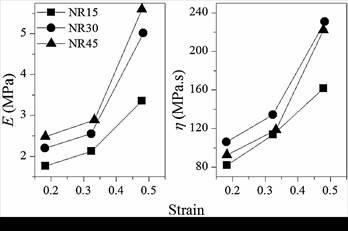
Fig. 3 shows the curve fitting of the Maxwell model to the stress relaxation experimental data at different strain levels.
3.2 Zener constitutive model
Fig. 2b shows the Zener constitutive model. Notice that the model consists of a Maxwell element with an additional linear spring. Both models are capable of representing stress relaxation since the spring of the Maxwell model and the free spring of the Zener model allow a sudden increase in strain. The constitutive equation of the Zener model is defined as:
where σ is the applied stress, E 1 and E 2 are the corresponding elastic modules, η is the viscosity, and the strain ε. Similarly to the Maxwell model, the Zener model is capable of representing stress relaxation (ε(t) constant), and the solution for σ(t) of eq. (3) is:
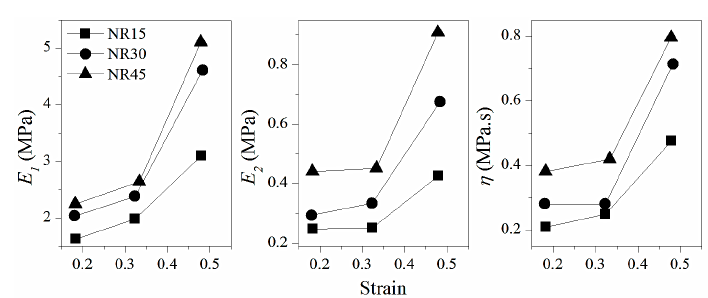
Fig. 4 shows the curve fitting of the Zener model to the experimental data.
3.3 Wiechert constitutive model
Fig. 2c shows the Wiechert model (or generalized Maxwell model), which consists of several Maxwell elements in parallel (the first damper is considered rigid). Mechanical models with multiple Maxwell elements enable the models to simulate adequately the viscoelastic behavior by providing multiple relaxation times (defined as τ=η/E ) because there is a single relaxation time associated with each Maxwell element [4]. Therefore, the constitutive equation of a single Maxwell element (eq. (1)) is applied for n elements, and then replaced in the equilibrium and kinematic eq. (5) and (6), respectively.
The solution of σ(t) for n elements is calculated as the sum of all elements as:
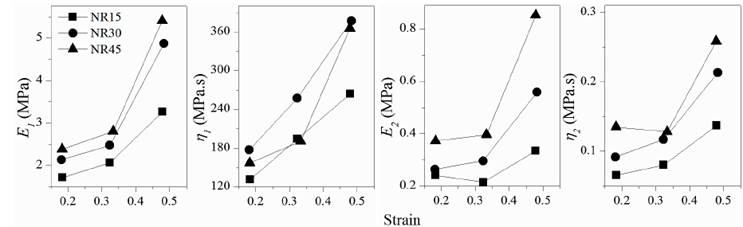
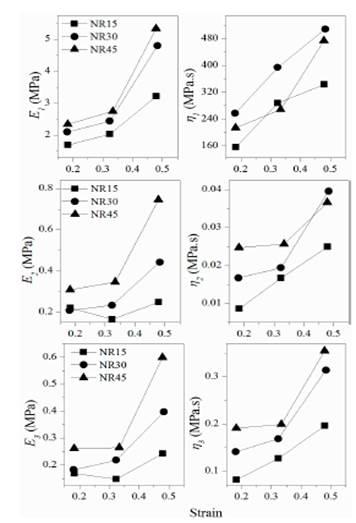
Fig. 5 and 6 show the curve fitting of the Wiechert model with n=2 and n=3 Maxwell elements, respectively.
4. Results and discussion
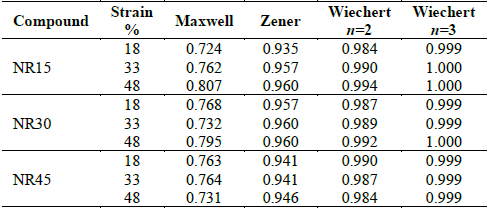
Table 1 shows the coefficient of determination R-squared (R2) for each model. The Maxwell model exhibited a mean value of 76.08±2.84%, while the Zener model showed a mean value of 95.10±0.98%, which indicate that a better fitting than the Maxwell model is obtained. The highest fitting values were obtained using the Wiechert model, and even with n=2 Maxwell elements, a determination coefficient as high as 98.86±0.35% can be observed.
Both the elastic and viscous parameters of the models were calculated and evaluated. Maxwell model parameters E and η calculated from the curve fitting are shown in Fig. 7. It is observed that, as the strain increases from 18 to 33 and finally to 48%, E increases for each compound exhibiting a non-linear behavior as obtained in the isochronous stress-strain diagrams in [12]. Additionally, it is shown that as the carbon black content as reinforcement increases, the calculated values of E, i.e., the elastic response of the compounds to a long-term compressive load, increase due to the stiffening effect of the filler content. This effect is because the reinforcement particles restrict movements of the elastomer chains and there is a reformation process of the filler transient network as the filler content varies, influencing both the elastic and viscous response of the material [2].
Likewise, the viscous response (η in Fig. 7) using the Maxwell model exhibits an increasing non-linear behavior as the strain increases. This behavior was also observed in the relaxation rates calculated experimentally because, as the viscous response of the compounds increases, materials are capable to relax more stress. Low stress relaxation rates indicate high elastic properties of rubber, while a large relaxation rate indicates a high viscosity. The relaxation rate of stress is associated with such structural characteristics of rubber, as well as the molecular weight distribution in a ramified chain, and gel content [5]. Additionally, it is known that larger amounts of carbon black increase damping properties because the filler transient network is the dominant factor governing the damping of the vulcanizates [2].
Similarly, to the Maxwell model, the calculated parameters of the Zener model E 1 , E 2 , and η are shown in Fig. 8. As expected, as the stiffness of the compounds increase, both the elastic and viscous behavior increase; and as the strain increases, a non-linear behavior is observed. Differences between the elastic and viscous responses of both Maxwell and Zener models are observed since the arrangement of the springs and dampers act differently. As the initial sudden strain is applied, large values of strain rates are induced; therefore, the damper of the Maxwell model can be considered as rigid (viscosity values in the range of 82 and 230 MPa.s) compared to those values obtained for the Zener model (ranging from 0.2 to 0.8 MPa.s). Then, the elastic response is predominant and comparable in magnitude to the free spring (E 1 ) of the Zener model.
Fig. 9 and 10 show the variations of the Wiechert model calculated parameters with n=2 and n=3 respectively, which exhibited the highest fitting values because multiple relaxation times enable the models to better mimic the viscoelastic behavior [4]. As analyzed previously, it is observed that the values of viscosity of the first damper are higher than the other dampers, and are considered rigid [14]. In both cases of the Wiechert model, both elastic and viscous responses increase in a non-linear relation as the applied strain increases. It is also observed that, as the number of Maxwell elements increase, the viscosity calculated of the additional dampers will decrease and can be considered less significant. Moreover, the Wiechert model with only n=3 Maxwell elements, results in coefficients of determination as high as 100% and no further Maxwell elements or complex models are required to simulate stress relaxation conditions as exhibited by rubber bearings applications.
In all models, it is observed that at least one spring exhibited an elastic modulus E ranging between 1.60 and 5.60 MPa, and at least one damper (except for the Zener model) exhibits increased values in the range of hundreds of MPa.s, and those values increase as the number of elements increases. This behavior is due to the configuration of the models, since the Zener model has a free spring allowing a sudden increase of stress and lower values in the viscous response.
Finally, it is observed that the elastic components of the NR15 compound in Fig. 9 and 10 (except for the first Maxwell element, E 1 ) at 33% of strain, a highly non-linear behavior is observed due to the lower carbon black content and due to the arrangement of the springs of the Wiechert model compared to the Maxwell and Zener models.
5. Conclusions
A comparative study of several phenomenological models is carried out to fit stress relaxation experimental data of carbon black-reinforced natural rubber compounds. The models used in this study have the capability of simulating the relaxation behavior under a constant compressive strain; however, different fitting values were observed depending on the arrangement and complexity of the model. It was observed that generalized models such as the Wiechert model (which exhibited the best fitting values, above 98.40%), are more adequate than simple models (which presented fitting values between 72.40 and 96.00%) since multiple relaxation times allow the models to better simulate the viscoelastic materials behavior. And even using the Wiechert model with two and three linear Maxwell elements to simulate simple loading states such as stress relaxation, adequate fitting values can be obtained. Moreover, both the elastic and viscous parameters calculated for each model exhibited a direct dependency on the carbon black content, and a non-linear relation dependent on the strain applied.
Generalized models with n=2 and n=3 Maxwell linear elements evaluated in this study are more adequate and are easy to implement in rubber components design processes such as rubber bearings and seals, which are subjected to long-term loading (such as stress relaxation, in which the viscoelastic properties are involved). Additionally, results obtained in this study can be used in finite element modeling for fitting the stress relaxation function of non-linear viscoelastic materials.