1. Introduction
Fig. 1 shows the distribution of the soil pressure below of the footing, and the distribution of the soil pressure is defined by the type and relative rigidity of the soil, the rigidity of the footing, and the depth of foundation at level of contact between the footing and the soil. Fig. 1(a) presents a concrete rigid footing resting in granular soil (sand or gravel). Fig. 1(b) shows a concrete rigid footing resting on a clay cohesive soil [1]. Now, to simplify the calculation, the hypothesis has been assumed that the soil is constituted by a bed of independent linear springs in such a way that the stresses that occur in the soil will be proportional to the displacements suffered by the foundation (the area of the real distribution is equal to the area of the uniform distribution).
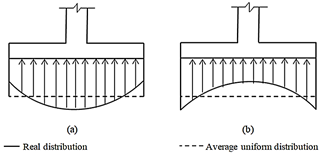
Source: Prepared by the author.
Figure 1 Distribution of the soil pressure below of the footing: (a) Rigid footing in non-cohesive soil (sand or gravel); (b) Rigid footing in clay cohesive soil.
The traditional design of footings generally involves a method of successive approximations. This process assumes a uniform distribution of stresses under the foundation, which represents an inadequate approach.
This work proposes direct equations to determine the effective depth and reinforcing steel areas of rectangular footings with different edge conditions for the calculation of bending moments, bending shear and punching shear for a linear distribution of stresses.
The works on mathematical models for foundation structures have been investigated successfully in several structural and geotechnical engineering problems. The main scientific contributions of several researchers in recent years are: Guler and Celep [2] presented the rectangular-shaped plate-column system by means of the Winkler foundation without tension under static and dynamic loads. Chen et al. [3] studied the hybrid composite plates on elastic foundations under nonlinear vibration. Smith-Pardo [4] presented a framework that considers the soil-structure interaction through simplified rocking foundation models. Shahin and Cheung [5] investigated the stochastic design charts for bearing capacity of strip footings. Zhang et al. [6] developed a nonlinear analysis of a finite beam resting on a Winkler foundation that takes into account the effect of the resistance of the beam on the soil. Agrawal and Hora [7] proposed the nonlinear interaction of a frame-footings-soil system under seismic loading. Rad [8] studied the static behavior of 2-D functionally graded circular plate with gradient thickness and elastic foundations for compound loads. Orbanich et al. [9] estimated the reinforcement and the repair with fiber composite materials for concrete foundation beams. Mohamed et al. [10] presented the Schmertmann general equation for settlement of shallow footings resting on saturated and unsaturated sands. Orbanich and Ortega [11] used the finite differences method for elastic foundation plates using internal and perimetric reinforcement beams rested on elastic foundations. Luévanos-Rojas et al. [12] developed a novel model for the design of rectangular isolated footings. Aristizabal-Ochoa [13] presented the general conditions for the stability of thin cross section columns rested on an elastic foundation. Barreto-Maya et al. [14] compared the load capacity between the experiment load tests and the mathematical formulations for deep foundations. Luévanos-Rojas [15] developed a mathematical model for the design of circular isolated footings. Uncuoğlu [16] investigated the load capacity for square footings on sand layer overlying clay. Luévanos-Rojas [17] developed a novel model for the design of boundary trapezoidal combined footings. Camero [18] presented a novel finite element method for the design of grade industrial floor slabs and pavements applying edge loads. Luévanos-Rojas [19] developed a mathematical model for the design of boundary rectangular combined footings limited to two opposite sides. Mohebkhah [20] estimated the load capacity of stone masonry strip footings over a clay trench. López-Chavarría et al. [21] proposed a novel mathematical model for the design of square isolated footings that takes into account the eccentric load on the footing (general case). Anil et al. [22] presented an analysis for footings of different shapes supported on sandy soil by the finite element method and experimental tests. Luévanos-Rojas et al. [23] presented a comparative study for design of trapezoidal and rectangular boundary combined footings using new models. Luévanos-Rojas et al. [24] proposed a novel mathematical model of design for the T-shaped combined footings. Yáñez-Palafox et al. [25] developed a modeling for the design of the strap combined footings.
The paper related to this work is: the design of rectangular combined footings of boundary with two opposite sides restricted that support two columns [19]. Thus, the review of the literature clearly shows that there is no close relationship with the topic of mathematical model for the design of rectangular footings that support one or more columns aligned on a longitudinal axis that is presented in this paper.
The first part of this document shows the most economical contact area on the soil (optimal surface) for the rectangular footings that support one or more columns aligned on a longitudinal axis. This paper presents a general model for the design of rectangular footings that support one or more columns aligned on a longitudinal axis. The pressure diagram considered in this document is linear. The recently published papers are restricted for same types of rectangular footings such as the rectangular isolated footings and rectangular combined footings (one paper for a restricted side and it considers that the resultant force is located on the longitudinal axis, and another paper for the two opposite sides restricted). Also, three numerical examples are shown to obtain the design of rectangular footings subject to an axial load and two moments in orthogonal directions in each column. First example is for a rectangular footing that supports a column (rectangular isolated footing). Second example is for a rectangular footing that supports two columns (rectangular combined footing). Third example is for a rectangular footing that supports three columns (rectangular combined footing).
2. Formulation of the general model
Fig. 1 of the part I shows a rectangular footing that supports “n” columns aligned on a longitudinal axis (X axis), and each column provides an axial load and two orthogonal bending moments.
Fig. 2 of the part I presents the pressure diagram below the rectangular footing, and also the soil pressure in each corner on the footing.
Stress anywhere on the footing contact surface due to soil pressure is presented below.
The stress in the main direction (longitudinal axis) of the X axis is (part I):
where: R is the sum of all the axial forces, M xT is the sum of all the bending moments around the X axis and M yT is the sum of all the bending moments around the Y axis, x is the distance parallel to the X axis measured from the center of gravity to the point in study, y is the distance parallel to the Y axis measured from the center of gravity to the point in study, L x is the distance in X direction of the footing, L y is the distance in Y direction of the footing. R, M xT , M yT , are presented in eq. (9)-(11) of the part I.
The stress in the transverse direction (Y axis) to the main direction (X axis) for any column by the following equation is obtained:
where: x n and y n are the stress coordinates of the column n, P n is the axial load in the column n, M xn is the bending moment around the X axis in the column n, M yn is the bending moment around the Y axis in the column n, w n is the width of the analysis surface for the column n in the main direction (X axis). The width of the analysis surface for the column located closest to the property line is w n = s + c 2n -1 + d/2 (If S≥d/2 →s =d/2, and if s < d/2 → s = s), and for the columns located in the central part of the footing the width of the analysis surface is w n = c 2n -1 + d (d is the effective deep, s is the distance from the face of the column to the free end of the footing). The eccentricity e xn for the column located in the property line is e xn = w n /2 - s - C 2n-1 /2, and for the columns located in the central part of the footing the eccentricity is e xn = 0.
2.1. Moments
Fig. 2 shows the critical sections for the bending moments according to the code are [26]: For the axes parallel to the X axis are: a 1, a 2, a 3 … a n−1, a n. For the axes parallel to the Y axis are: b 1, b 2, b 3 … b n−1, b n, and d 1, d 2, d 3 … d n−1, d n.
2.1.1. Moment around the xn’ - xn’ axis of 0 ≤ yn ≤ Ly/2
The shear force V yn is obtained by the pressure volume of the surface formed by the x n ´ - x n ´ axis with a width w n and the free end (top side of the Fig. 2) of the footing:
Now, the integration of the shear force is the bending moment at any point, the basic equation is presented as follows:
where: M xn´ is the moment around the x n’ axis and V yn is the shear force at a distance y n .
Integrating eq. (4) the bending moment at any point is obtained:
Substituting y n = L y /2 and M xn´ = 0 into eq. (6), the constant C 1 is found:
Now, substituting eq. (7) into eq. (6), the general equation for bending moments is shown as follows:
Substituting y n = c 2n /2 into eq. (8), the moment M an on the a n axis is obtained:
2.1.2. Moment around the y-y axis considered the left part of the footing
The shear force V xk is found by the pressure volume of the surface formed by the y - y axis with a width L y and the free end (left side of the Fig. 2) of the footing:
where: the first part of eq. (10) and (11) represents the loads due to the columns and the second part represents the soil pressure.
Note: The shear forces due to column loads are not considered, when analyzed from the free end of the footing to the first column.
Now, the integration of the shear force is the bending moment at any point, the basic equation is presented as follows:
where: M y is the moment around the y axis and V xk is the shear force at a distance x k .
Integrating the eq. (11) of the soil pressure and the bending moment at any point from the free end of the footing to the first column is obtained:
Substituting x k = L x /2 and M y = 0 into eq. (13) and the constant C 2 is obtained:
Now, substituting eq. (14) into eq. (13), the general equation for bending moments at any point from the free end of the footing to the first column is shown as follows:
Now, the eq. (11) of part I due to the columns loads are considered for the analysis from the column 1 until the last column. The bending moment at a distance “x k ” between the columns is:
where: My1 is bending moment due to the soil pressure, and My2 is bending moment due to column loads.
The eq. (15) and (16) are added to obtain the general equation of the bending moments at any point from the first column until the last column, and equation is represented as follow:
Substituting x k = L x /2 - L a + c 1 /2 into eq. (15), the bending moment M b1 on the b 1 axis is obtained:
Now, substituting the coordinates in X direction at the junction of the column face with the footing to obtain the bending moments around of the axes b 2, b 3, … b n-1 , b n, and d 1, d 2, d 3, … d n-1 , d n.
2.2. Bending shear
Critical sections of the bending shear are presented at a distance d from the junction of the column with the footing, and these sections appear on en, fn and gn axes (see Fig. 3).
2.2.1. Bending shear on the x n ´ - x n ´ axis
Substituting y n = c 2n /2 + d into eq. (4), the bending shear V en on the e n axis of the footing is obtained:
2.2.2. Bending shear on the y - y axis
Substituting x k = L x /2 - L a + c 1 /2 + d into the second part of the eq. (11), the bending shear V f1 on the f 1 axis of the footing is obtained:
where: the values of s are, if S ≥ d → s = d, and if s < d → s = s.
Now, substituting the coordinates in X direction at a distance d from the junction of the column with the footing into eq. (11) to obtain the bending shear in the axes f 2, f 3, … f n-1 , f n, and g 1, g 2, g 3, … g n-1 , g n.
2.3. Punching shear
Critical section for the punching shear appears at a distance d/2 from the junction of the column with the footing in the two directions (see Fig. 4).
2.3.1. Punching shear for the boundary column
Critical section for the punching shear is presented in the rectangular section formed by the dotted surface of the boundary column. Punching shear acting on the footing V p1 is the force P 1 acting on column 1 subtracting the pressure volume of the surface formed by the dotted surface of the boundary column:
2.3.2. Punching shear for the inner column
Critical section for the punching shear is presented in the rectangular section formed by the dotted surface of the inner column. Punching shear acting on the footing V pn is the force P n acting on column n subtracting the pressure volume of the surface formed by the dotted surface of the inner column:
3. Numerical problems
Three numerical examples are presented below: Example 1 is for a rectangular footing that supports a column. Example 2 is for a rectangular footing that supports two columns. Example 3 is for a rectangular footing that supports three columns.
The thickness for the three examples is determined as follows: First, a minimum thickness is proposed according to the code of 25 cm [26], and then the thickness is revised to meet with the following conditions: bending moments, bending shear, and punching shear.
3.1. Example 1
The design of a rectangular footing (rectangular isolated footing) that supports a square column with the following information are presented: the column is of 40x40 cm; H = 2.0 m; P D1 = 600 kN; P L1 = 300 kN; M Dx1 = 200 kN-m; M Lx1 = 100 kN-m; M Dy1 = 100 kN-m; M Ly1 = 50 kN-m; f’ c = 35 MPa; f y = 420 MPa; q a = 250 kN/m 2 ; γ ppz = 24 kN/m 3 ; γ pps = 15 kN/m 3 . Where: H is the depth of the footing, P D1 is the dead load, P L1 is the live load, M Dx1 is the moment around the X axis of the dead load, M Lx1 is the moment around the X axis of the live load, M Dy1 is the moment around the Y axis of the dead load, M Ly1 is the moment around the Y axis of the live load.
The load and moments that act on soil are: P 1 = 900 kN; M x1 = 300 kN-m; M y1 = 150 kN-m.
The thickness that meets the bending moments, bending shear, and punching shear is of 45 cm.
Substituting the values of σ p = 215.95 kN/m 2 , P 1 = 900 kN, M x1 = 300 kN-m, M y1 = 150 kN-m, L a = L x /2 into eq. (15)-(23) of part I and using the MAPLE-15 software are obtained: S tmin = 8.27 m 2 , L x = 2.03 m, L y = 4.07 m, σ 1 = 215.95 kN/m 2 , σ 2 = 108.86 kN/m 2 , σ 3 = 108.86 kN/m 2 , σ 4 = 1.77 kN/m 2 .
Now the practical dimensions of the rectangular footing that supports a square column are: L x = 2.05 m, L y = 4.10 m.
Substituting the values of L x = 2.05 m, L y = 4.10 m in the same MAPLE-15 software are obtained: S tmin = 8.40 m 2 , L x = 2.05 m, L y = 4.10 m, σ 1 = 211.55 kN/m 2 , σ 2 = 107.08 kN/m 2 , σ 3 = 107.08 kN/m 2 , σ 4 = 2.61 kN/m 2 .
The load and the bending moments around of the X and Y axes (factored mechanical elements) are [26]: P u1 = 1200 kN; M ux1 = 400 kN-m; M uy1 = 200 kN-m.
3.2. Example 2
The design of a rectangular footing (rectangular combined footing) that supports two square columns with the following information are presented: the columns are of 40x40 cm; H = 2.0 m; L 1 = 6.00 m; P D1 = 600 kN; P L1 = 300 kN; M Dx1 = 200 kN-m; M Lx1 = 100 kN-m; M Dy1 = 100 kN-m; M Ly1 = 50 kN-m; P D2 = 1200 kN; P L2 = 600 kN; M Dx2 = 400 kN-m; M Lx2 = 200 kN-m; M Dy2 = 200 kN-m; M Ly2 = 100 kN-m; f’ c = 35 MPa; f y = 420 MPa; q a = 250 kN/m 2 ; γ ppz = 24 kN/m 3 ; γ pps = 15 kN/m 3 .
The loads and moments that act on soil are: P 1 = 900 kN; M x1 = 300 kN-m; M y1 = 150 kN-m; P 2 = 1800 kN; M x2 = 600 kN-m; M y2 = 300 kN-m.
The thickness that meets the bending moments, bending shear, and punching shear is of 80 cm.
Substituting the values of σ p = 212.80 kN/m 2 , P 1 = 900 kN, M x1 = 300 kN-m, M y1 = 150 kN-m, P 2 = 1800 kN, M x2 = 600 kN-m, M y2 = 300 kN-m into eq. (15)-(23) of part I and using the MAPLE-15 software are obtained: S tmin = 21.99 m 2 , L a = 0.20 m, L x = 8.07 m, L y = 2.73 m, M xT = 900.00 kN-m, M yT = 0.00 kN-m, R = 2700 kN, σ 1 = 212.80 kN/m 2 , σ 2 = 212.80 kN/m 2 , σ 3 = 32.71 kN/m 2 , σ 4 = 32.71 kN/m 2 .
Now the practical dimensions of the rectangular footing that supports two square columns are: L x = 8.10 m, L y = 2.75 m.
Substituting the values of L x = 8.10 m, L y = 2.75 m in the same MAPLE-15 software are obtained: S tmin = 22.27 m 2 , L a = 0.22 m, L x = 8.10 m, L y = 2.75 m, M xT = 900.00 kN-m, M yT = 1.00 kN-m, R = 2700 kN, σ 1 = 209.40 kN/m 2 , σ 2 = 209.33 kN/m 2 , σ 3 = 33.09 kN/m 2 , σ 4 = 33.02 kN/m 2 .
The loads and the bending moments around of the X and Y axes (factored mechanical elements) are [26]: P u1 = 1200 kN; M ux1 = 400 kN-m; M uy1 = 200 kN-m, P u2 = 2400 kN; M ux2 = 800 kN-m; M uy2 = 400 kN-m.
The factored resultant loads and the factored resultant bending moments by Eqs. (16) to (18) of part I are obtained: R u = 3600 kN, M uxT = 1200 kN-m, M uyT = 60 kN-m.
3.3. Example 3
The design of a rectangular footing (rectangular combined footing) that supports three square columns with the following information are presented: the columns are of 40x40 cm; H = 2.0 m; L 1 = 6.00 m; P D1 = 600 kN; P L1 = 300 kN; M Dx1 = 200 kN-m; M Lx1 = 100 kN-m; M Dy1 = 100 kN-m; M Ly1 = 50 kN-m; P D2 = 1200 kN; P L2 = 600 kN; M Dx2 = 400 kN-m; M Lx2 = 200 kN-m; M Dy2 = 200 kN-m; M Ly2 = 100 kN-m; P D3 = 1200 kN; P L3 = 600 kN; M Dx3 = 400 kN-m; M Lx3 = 200 kN-m; M Dy3 = 200 kN-m; M Ly3 = 100 kN-m; f’ c = 35 MPa; f y = 420 MPa; q a = 250 kN/m 2 ; γ ppz = 24 kN/m 3 ; γ pps = 15 kN/m 3 .
The loads and moments that act on soil are: P 1 = 900 kN; M x1 = 300 kN-m; M y1 = 150 kN-m; P 2 = 1800 kN; M x2 = 600 kN-m; M y2 = 300 kN-m; P 3 = 1800 kN; M x3 = 600 kN-m; M y3 = 300 kN-m.
The thickness that meets the bending moments, bending shear, and punching shear is of 80 cm.
Substituting the values of σ p = 212.80 kN/m 2 , P 1 = 900 kN, M x1 = 300 kN-m, M y1 = 150 kN-m, P 2 = 1800 kN, M x2 = 600 kN-m, M y2 = 300 kN-m, P 3 = 1800 kN, M x3 = 600 kN-m, M y3 = 300 kN-m into eq. (15)-(23) of part I and using the MAPLE-15 software are obtained: S tmin = 37.47 m 2 , L a = 0.20 m, L x = 14.47 m, L y = 2.59 m, M xT = 1500.00 kN-m, M yT = 0.00 kN-m, R = 4500 kN, σ 1 = 212.80 kN/m 2 , σ 2 = 212.80 kN/m 2 , σ 3 = 27.37 kN/m 2 , σ 4 = 27.37 kN/m 2 .
Now the practical dimensions of the rectangular footing that supports two square columns are: L x = 14.50 m, L y = 2.60 m.
Substituting the values of L x = 14.50 m, L y = 2.60 m in the same MAPLE-15 software are obtained: S tmin = 37.70 m 2 , L a = 0.22 m, L x = 14.50 m, L y = 2.60 m, M xT = 1500.00 kN-m, M yT = 1.00 kN-m, R = 4500 kN, σ 1 = 211.19 kN/m 2 , σ 2 = 211.17 kN/m 2 , σ 3 = 27.56 kN/m 2 , σ 4 = 27.53 kN/m 2 .
The loads and the bending moments around of the X and Y axes (factored mechanical elements) are [26]: P u1 = 1200 kN; M ux1 = 400 kN-m; M uy1 = 200 kN-m, P u2 = 2400 kN; M ux2 = 800 kN-m; M uy2 = 400 kN-m, P u3 = 2400 kN; M ux3 = 800 kN-m; M uy3 = 400 kN-m.
The factored resultant loads and the factored resultant bending moments by Eqs. (16) to (18) of part I are obtained: R u = 6000 kN, M uxT = 2000 kN-m, M uyT = - 100 kN-m.
4. Results
One way to verify the model proposed in this document is:
Substituting y n = L y /2 into eq. (8), and the moment around the xn´-xn´ axis is M xn´ = 0.
Now, substituting x k = L x /2 into eq. (15), and the moment around the y1-y1 axis is M y1 = 0.
Substituting x k = - L x /2 into eq. (17) and the moment around the y-y axis is M y = 0.
Now, substituting y n = L y /2 into eq. (4) and the shear force on the xn´-xn´ axis is V yn = 0.
Substituting x k = L x /2 into eq. (11) considering only the second part that represents the soil pressure, and the shear force on the y1-y1 axis is V xk = 0.
Now, substituting x k = - L x /2 into eq. (11), and the shear force on the y-y axis is V xk = 0.
Therefore the equations for the bending moments and the shear forces are verified by equilibrium.
4.1. Example 1
Substituting the corresponding values into eq. (9)-(15) to obtain the bending moments that act on the critical sections of the rectangular isolated footing are shown below: M a1 = 671.68 kN-m; M b1 = 270.31 kN-m.
After making different proposals, the effective depth is d = 37.00 cm, r = 8.00 cm, t = 45.00 cm.
Substituting the corresponding values into eq. (19)-(20) to obtain the bending shear forces that act on the critical sections of the rectangular isolated footing are shown below: V e1 = - 568.20 kN; V f1 = - 367.43 kN. Now, the allowable bending shear forces by the concrete are: ∅ v V ce1 = 648.42 kN; ∅ v V cf1 = 1296.84 kN. Then, the two bending shear forces satisfy with the code [26].
Now, substituting the corresponding values into eq. (22) to obtain the punching shear force that acts on the critical section of the rectangular isolated footing is shown below: V p1 = 1115.35 kN. Now, the allowable punching shear forces by the concrete are: ∅ v V cp1 = 2922.64 kN, ∅ v V cp1 = 3236.86 kN, ∅ v V cp1 = 1891.12 kN. Then, the punching shear force satisfies with the code [26].
The reinforcement steel areas for the rectangular isolated footing that result of the bending moments are shown below: A sy = 50.39 cm 2; A sx = 19.50 cm 2, and the minimum steel areas according to the code are [26]: A symin = 25.28 cm 2; A sxmin = 50.57 cm 2. Hence, the reinforcement steel areas for the design of the rectangular isolated footing are: A sy = 50.39 cm 2; A sx = 50.57 cm 2. The proposed steel areas are: A sy = 50.70 cm 2 (10Ø1”) spaced at 20.56 cm; A sx = 50.70 cm 2 (10Ø1”) spaced at 43.33 cm.
4.2. Example 2
Substituting the corresponding values into eq. (9), (15) and (17) to obtain the bending moments that act on the critical sections of the rectangular combined footing are shown below: M a1 = 457.908 kN-m; M a2 = 915.80 kN-m; M b1 = 0.09 kN-m; M d1= - 400.33kN-m; M b2 = 943.58 kN-m; M d2 = 692.53 kN-m; M max12 = - 1540.55kN-m (maximum bending moment between the column 1 and column 2) in x max12 = 1.37 m (position of the maximum bending moment between the column 1 and column 2).
The maximum bending moment between the column 1 and column 2 is obtained as follows: First, the position of the maximum bending moment is located from the equation of the shear forces, i.e., when the shear force is zero, the maximum moment is obtained.
After making different proposals, the effective depth is d = 72.00 cm, r = 8.00 cm, t = 80.00 cm.
The bending shear forces that act on the critical sections of the rectangular combined footing by eq. (19)-(11), and the allowable bending shear forces for the concrete by the code are obtained [26] (see Table 1).
Table 1 Bending shear forces of the example 2.
| Axis | Shear force that acts (kN) | Allowable shear force (kN) | Width of analysis (m) |
|---|---|---|---|
| e 1 | −319.05 | 467.79 | 0.76 |
| e 2 | −638.10 | 689.37 | 1.12 |
| f 1 | 0* | 1692.65 | 2.75 |
| g 1 | 687.96 | 1692.65 | 2.75 |
| f 2 | −1165.61 | 1692.65 | 2.75 |
| g 2 | 422.02 | 1692.65 | 2.75 |
* The axis falls outside of the footing
Source: Prepared by the author.
Then, the bending shear forces satisfy with the ACI code [26].
The punching shear force that act on the critical sections of the rectangular combined footing by eq. (22) and (24), and the allowable punching shear forces for the concrete by the code are obtained [26] (see Table 2).
Table 2 Punching shear forces of the example 2.
| Analysis section | Shear force that acts (kN) | Allowable shear force (kN) | Critical perimeter (m) |
|---|---|---|---|
| Column 1 (boundary column) | 1057.24 | 4948.69 | 2.68 |
| 8101.84 | |||
| 3202.09 | |||
| Column 2 (inner column) | 2198.61 | 8272.44 | 4.48 |
| 11347.38 | |||
| 5352.76 |
Source: Prepared by the author.
Then, the two punching shear forces satisfy with the ACI code [26].
The reinforcement steel areas for the rectangular combined footing that result of the bending moments are shown below (see Table 3).
Table 3 Reinforcement steel of the example 2.
| Direction of the steel | Steel location | Steel area (cm2) | |
|---|---|---|---|
| Y axis | Under column 1 (width of c 1 + s + d/2) | Main steel | 17.21 |
| Minimum steel | 18.24 | ||
| Proposed steel | 20.28(4Ø1”) | ||
| Under column 2 (width of c 3 + d) | Main steel | 34.70 | |
| Minimum steel | 26.88 | ||
| Proposed steel | 35.49(7Ø1”) | ||
| Steel at the bottom (width of L x − c 1 − c 3 − s − 3d/2) | Temperature steel | 89.57 | |
| Proposed steel | 91.20(32Ø3/4”) | ||
| Steel at the top (width of L x ) | Temperature steel | 116.64 | |
| Proposed steel | 116.85(41Ø3/4”) | ||
| X axis | Steel at the Bottom (width of L y ) | Main steel | 35.11 |
| Minimum steel | 66.00 | ||
| Proposed steel | 70.98(14Ø1”) | ||
| Steel at the Top (width of L y ) | Main steel | 57.80 | |
| Minimum steel | 66.00 | ||
| Proposed steel | 70.98(14Ø1”) | ||
Source: Prepared by the author.
4.3. Example 3
Substituting the corresponding values into eq. (9), (15) and (17) to obtain the bending moments that act on the critical sections of the rectangular combined footing are shown below: Ma1 = 433.44 kN-m; Ma2 = 866.88 kN-m; Ma3 = 866.88 kN-m; Mb1 = 0.08 kN-m; Md1 = − 406.22 kN-m; Mb2 = − 73.36 kN-m; Md2 = 448.43 kN-m; Mb3 = 198.02 kN-m; Md3 = − 123.47 kN-m; Mmax12 = − 1797.11 kN-m (maximum bending moment between the column 1 and column 2) in xmax12 = 4.17 m (position of the maximum bending moment between the column 1 and column 2); Mmax23 = − 1794.99 kN-m (maximum bending moment between the column 2 and column 3) in xmax23 = − 1.71 m (position of the maximum bending moment between the column 2 and column 3).
The maximum bending moment between the two columns is obtained as follows: First, the position of the maximum bending moment is located from the equation of the shear forces, i.e., when the shear force is zero, the maximum moment is obtained.
After making different proposals, the effective depth is d = 72.00 cm, r = 8.00 cm, t = 80.00 cm.
The bending shear forces that act on the critical sections of the rectangular combined footing by eq. (19), (20) and (11), and the allowable bending shear forces for the concrete by the code are obtained [26] (see Table 4).
Table 4 Bending shear forces of the example 3.
| Axis | Shear force that acts (kN) | Allowable shear force (kN) | Width of analysis (m) |
|---|---|---|---|
| e1 | −290.58 | 467.79 | 0.76 |
| e2 | −581.16 | 689.37 | 1.12 |
| e3 | −581.16 | 689.37 | 1.12 |
| f1 | 0* | 1600.32 | 2.60 |
| g1 | 768.99 | 1600.32 | 2.60 |
| f2 | −879.44 | 1600.32 | 2.60 |
| g2 | 759.28 | 1600.32 | 2.60 |
| f3 | −988.95 | 1600.32 | 2.60 |
| g3 | 601.45 | 1600.32 | 2.60 |
* The axis falls outside of the footing
Source: Prepared by the author.
Then, the bending shear forces satisfy with the code [26].
The punching shear forces acting on the critical section of the rectangular combined footing by eq. (22) and (24) are obtained, and the allowable punching shear forces for the concrete by the code are obtained [26] (see Table 5).
Table 5 Punching shear forces of the example 3.
| Analysis section | Shear force that acts (kN) | Allowable shear force (kN) | Critical perimeter (m) |
|---|---|---|---|
| Column 1 (boundary column) | 1070.95 | 4948.69 | 2.68 |
| 8101.84 | |||
| 3202.09 | |||
| Column 2 (inner column) | 2202.51 | 8272.44 | 4.48 |
| 11347.38 | |||
| 5352.76 | |||
| Column 3 (inner column) | 2189.98 | 8272.44 | 4.48 |
| 11347.38 | |||
| 5352.76 |
Source: Prepared by the author.
Then, the two punching shear forces satisfy with the ACI code [26].
The reinforcement steel areas for the rectangular combined footing that result of the bending moments are shown below (see Table 6).
Table 6 Reinforcement steel of the example 3.
| Direction of the steel | Steel location | Steel area (cm2) | |
|---|---|---|---|
| Y axis | Under column 1 (width of c 1 + s + d/2) | Main steel | 16.27 |
| Minimum steel | 18.24 | ||
| Proposed steel | 20.28(4Ø1”) | ||
| Under column 2 (width of c 3 + d) | Main steel | 32.79 | |
| Minimum steel | 26.88 | ||
| Proposed steel | 35.49(7Ø1”) | ||
| Under column 3 (width of c 5 + d) | Main steel | 32.79 | |
| Minimum steel | 26.88 | ||
| Proposed steel | 35.49(7Ø1”) | ||
| Steel at the bottom (width of L x − c 1 − c 3 - c 5 − s − 5d/2) | Temperature steel | 165.60 | |
| Proposed steel | 168.15(59Ø3/4”) | ||
| Steel at the top (width of L x ) | Temperature steel | 208.80 | |
| Proposed steel | 210.90(74Ø3/4”) | ||
| X axis | Steel at the Bottom (width of L y ) | Main steel | 16.58 |
| Minimum steel | 62.40 | ||
| Proposed steel | 65.91(13Ø1”) | ||
| Steel at the Top (width of L y ) | Main steel | 67.76 | |
| Minimum steel | 62.40 | ||
| Proposed steel | 70.98(14Ø1”) | ||
Source: Prepared by the author.
5. Conclusions
The model presented in this paper applies only for design of the rectangular footings that support n columns aligned on a longitudinal axis, this model assumes that the footings should be rigid and the supporting soil layers elastic, which meet expression of the bidirectional bending, i.e., the pressure variation behaves linearly.
This paper concludes the following:
The thickness for the rectangular isolated footing is governed by the bending shear on the e1 axis, and the thicknesses for the rectangular combined footings that support two and three columns are governed by the bending shear on the e2 axes.
This document is not limited as those presented by other authors such as: “Design of isolated footings of rectangular form using a new model” by Luévanos-Rojas [12], this model considers only a column. “A new model for the design of rectangular combined footings of boundary with two opposite sides restricted” by Luévanos-Rojas [19], this model considers only two columns.
The proposed model is more suited to the real conditions with respect to the classical model, because the proposed model takes into account the linear soil pressure and the classical model considers a uniform pressure (maximum pressure) in all the contact surface, when the loads and moments act on the footing.
The proposed model for design of rectangular footings subjected to an axial load and two moments in orthogonal directions in each column can be used for the following considerations:
The main advantage of this document over other documents is that this model can be applied to one (rectangular isolated footings), two or more columns that are supported by a rectangular footing, and it is also not restricted to that the resultant force must be located on a longitudinal axis.
The next investigations can be: 1) Modeling for the design of foundation slabs and/or rafts. 2) When another type of soil is presented under the footing, by example in 100% cohesive soils (clay soils) or in 100% granular soils (sandy soils), the pressure diagram is different (nonlinear) and should be treated as shown in Fig. 1.






































