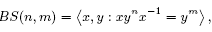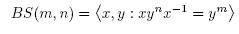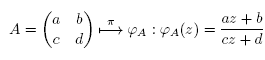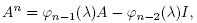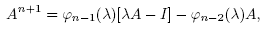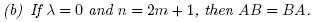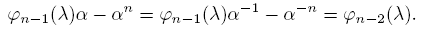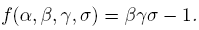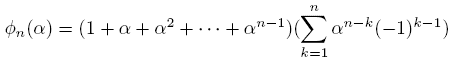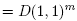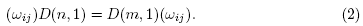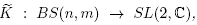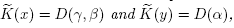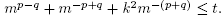1. Introduction
Baumslag-Solitar groups constitute an important family of examples or counterexamples in the theory of combinatorial groups, see [2], [7], [5] and [4]. These groups were first introduced by G. Baumslag and D. Solitar in [2] in order to get non-Hopfian one-relator group presentations and they are given by the following short presentation
where m and n are non zero integer numbers.
Although the principal focus of the study of non-abelian representations has been on the family of classical knot groups, in particular on the collection of 2-bridge classical knot groups, we want to start a classification of the PSL(2,  ) non abelian representations on the family of Baumslag-Solitar groups. Recently, in a joint work with O. Salazar and J. Mira, see [8], we proved that BS(n, n +1) are the only Baumslag-Solitar groups that correspond to groups of 2-bridge non-classical virtual knots. From this we consider that the study of some properties of the Baumslag-Solitar groups becomes an important aim, in particular the classification of their non-abelian representations into the group PSL(2,
) non abelian representations on the family of Baumslag-Solitar groups. Recently, in a joint work with O. Salazar and J. Mira, see [8], we proved that BS(n, n +1) are the only Baumslag-Solitar groups that correspond to groups of 2-bridge non-classical virtual knots. From this we consider that the study of some properties of the Baumslag-Solitar groups becomes an important aim, in particular the classification of their non-abelian representations into the group PSL(2,  ). It is well known that there exists an isomorphism between the orientation preserving isometries of
). It is well known that there exists an isomorphism between the orientation preserving isometries of 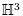 and PSL(2,
and PSL(2,  ).
).
In this paper we present a collection of algebraic varieties that encode information about the set of equivalence classes of non-abelian representations of BS(n, m). The definition of these algebraic varieties uses a classification of the conjugacy classes of elements of the Möbius group via diagonal matrices and Jordan forms which is not the standard classification of elements of the Möbius group given in [3]. It is worth noting that for |m| > 1, BS(1,m) is a linear group. It would seem that this result forms part of the folklore in the scope of Baumslag-Solitar group theory. As a consequence, there is no article in the literature which contains a formal proof of such fact. However, we can get one from mathoverflow. From the results displayed in this paper and some restrictions given in [7] and [1] about the residually finiteness of the Baumslag-Solitar groups, we prove that BS(n, m) only admits a faithful representation into SL(2,  ) when n = 1 and |m| > 1. This result overlaps with what was mentioned in the previous paragraph, but we propose a different method that might be of interest for those working in Kleinian and Fuchsian groups. Moreover, if rm denotes the image of BS(1,m), for |m| > 1, into PSL(2,
) when n = 1 and |m| > 1. This result overlaps with what was mentioned in the previous paragraph, but we propose a different method that might be of interest for those working in Kleinian and Fuchsian groups. Moreover, if rm denotes the image of BS(1,m), for |m| > 1, into PSL(2,  ), then we show that Tm is an elementary and non-discrete subgroup of Möbius transformations.
), then we show that Tm is an elementary and non-discrete subgroup of Möbius transformations.
This paper is organized as follows. In section 2 we give a short list of preliminaries concerning Möbius transformations. We also recall the definition of SL(2,  )-representations, residually finite groups and linear groups. Then, in Section 3 we show the existence of non-abelian representations of the Baumslag-Solitar groups and provide a classification of them into two families, pseudo-parabolic and pseudo-elliptic representations. We give functions of certain algebraic affine varieties into each of them. Finally, in Section 4 we show that BS(1, m) is a linear group, for |m| > 1. Moreover, we prove that its representation image in the Möbius transformations group is an elementary and non discrete subgroup.
)-representations, residually finite groups and linear groups. Then, in Section 3 we show the existence of non-abelian representations of the Baumslag-Solitar groups and provide a classification of them into two families, pseudo-parabolic and pseudo-elliptic representations. We give functions of certain algebraic affine varieties into each of them. Finally, in Section 4 we show that BS(1, m) is a linear group, for |m| > 1. Moreover, we prove that its representation image in the Möbius transformations group is an elementary and non discrete subgroup.
2. Notation and preliminary results
In this section we introduce a short list of definitions, notations and some results necessary to understand this article.
2.1. Möbius transformations
The set of Möbius transformations , with a,b,c,d Є
, with a,b,c,d Є  and ad ≠ bc = 0, acting on
and ad ≠ bc = 0, acting on , is denoted by
, is denoted by  . This set has some additional structure; it is a group under composition of transformations. Besides, the homomorphism
. This set has some additional structure; it is a group under composition of transformations. Besides, the homomorphism , where
, where
has kernel {±I}, and it provides a natural identification between  and PSL(2,
and PSL(2,  ).
).
We use tr(A) and At to denote the trace and the transpose of a matrix A.
The following definition come from the correspondence between SL(2,  ) and the group of Möbius transformations PSL(2,
) and the group of Möbius transformations PSL(2,  ).
).
Definition 2.1. [3] Let A (A ≠ I) be a matrix in SL(2,  ), then A is a parabolic matrix if and only if tr2(A) =4, A is an elliptic matrix if and only if tr2(A) Є [0,4), A is a hyperbolic matrix if and only if tr2(A) Є (4, +∞), and A is a strictly loxodromic matrix if and only of tr2(A)
), then A is a parabolic matrix if and only if tr2(A) =4, A is an elliptic matrix if and only if tr2(A) Є [0,4), A is a hyperbolic matrix if and only if tr2(A) Є (4, +∞), and A is a strictly loxodromic matrix if and only of tr2(A) 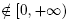 .
.
The following notation will be useful in order to simplify the proof and certain definitions given in the rest of this paper.
We say that A Є SL(2,  ) is a scalar matrix if A = D(δ), with δ2 = 1, and I = D(1).
) is a scalar matrix if A = D(δ), with δ2 = 1, and I = D(1).
The purpose of the next theorem is to classify the conjugacy classes of the matrices in SL(2,  ). This classification involves diagonal matrices and matrices in Jordan form. Another classification using the theory of fixed points of Moobius transformations is given in [3].
). This classification involves diagonal matrices and matrices in Jordan form. Another classification using the theory of fixed points of Moobius transformations is given in [3].
Theorem 2.2. Every non scalar matrix A in SL(2,  ) is a conjugate of one of the following matrices: D(1, 1), D(1, -1) or D(6).
) is a conjugate of one of the following matrices: D(1, 1), D(1, -1) or D(6).
Moreover, if A is taken in PSL(2,  ), then it is conjugate to D(1, 1) or D(δ).
), then it is conjugate to D(1, 1) or D(δ).
Proof. Let A Є SL(2,  ) be a non scalar matrix with characteristic polynomial
) be a non scalar matrix with characteristic polynomial  and consider the following cases.
and consider the following cases.
Case 1: If  , then, because A is not a scalar matrix, its minimal polynomial must be equal to
, then, because A is not a scalar matrix, its minimal polynomial must be equal to 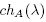 , hence, from the canonical Jordan form, the matrix A is a conjugate of some matrix of the form D(1 , δ ), where δ2 = 1.
, hence, from the canonical Jordan form, the matrix A is a conjugate of some matrix of the form D(1 , δ ), where δ2 = 1.
Case 2 If 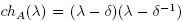 , then A is a diagonalizable matrix, therefore the matrix A is a conjugate of some matrix of the form D(δ), where δ2 =1
, then A is a diagonalizable matrix, therefore the matrix A is a conjugate of some matrix of the form D(δ), where δ2 =1
For the last part, note that, in PSL(2,  ), D(1 , - 1) = D( -1 , 1). Because D(1, i)D(1,1)D-1, = D( -1,1), then D(1, -1) and D(1,1) are in the same conjugacy class.
), D(1 , - 1) = D( -1 , 1). Because D(1, i)D(1,1)D-1, = D( -1,1), then D(1, -1) and D(1,1) are in the same conjugacy class. 
Let A Є SL(2,  ), we define the norm of A, denoted ||A||, as
), we define the norm of A, denoted ||A||, as
The topology on SL(2,  ) induced by this norm is denoted by
) induced by this norm is denoted by .
.
The homomorphism Π induces the quotient topology  on
on  with respect to which Π is continuous. Besides,
with respect to which Π is continuous. Besides,  has the topology
has the topology  of uniform convergence with respect to the chordal metric on
of uniform convergence with respect to the chordal metric on  These topologies are the same. (see [3].
These topologies are the same. (see [3].
Definition 2.3. A subgroup G of SL(2,  ) is discrete if and only if the relative topology on G is the discrete topology.
) is discrete if and only if the relative topology on G is the discrete topology.
The proof of the following lemma can be found in [3].
Lemma 2.4. A subgroup G of SL(2,  ) is discrete if and only if for each positive k, the set
) is discrete if and only if for each positive k, the set 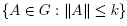 is finite.
is finite.
Definition 2.5. A subgroup G of  is said to be elementary if and only if any two elements of infinite order have a common fixed point.
is said to be elementary if and only if any two elements of infinite order have a common fixed point.
A subgroup G of  acts discontinuously on a G-invariant disc Δ (or on the half-plane), if for every compact
acts discontinuously on a G-invariant disc Δ (or on the half-plane), if for every compact  except for a finite number of g Є G.
except for a finite number of g Є G.
Definition 2.6. A non-elementary subgroup G of  is a Kleinian group if it is discrete. If, moreover, G has a G-invariant disc Δ on which G acts discontinuously, we say that G is a Fuchsian group.
is a Kleinian group if it is discrete. If, moreover, G has a G-invariant disc Δ on which G acts discontinuously, we say that G is a Fuchsian group.
The proof of the following theorem can be found in [3].
Theorem 2.7.
Let
 with
with and not of order two. Let θ :
and not of order two. Let θ :  , where
, where  . If for some n,
. If for some n,  = f, then (f, g) is elementary.
= f, then (f, g) is elementary.
Therefore, any elementary Fuchsian group is either cyclic or it is conjugate to some group (f, g), where g(z) = kz (k > 1) and f (z) = -1/z.
2.2. SL(2, C )-representations of Baumslag-Solitar groups
In this section we will give some background material concerning the representation and character of the Baumslag-Solitar groups.
A representation of BS(n, m) into SL(2,  ) is understood as a homomor-phism p :
) is understood as a homomor-phism p :  . The set of all representations is denoted by R(BS(n, m)). It is not hard to verify that R (BS(n, m)) can be endowed with the structure of an affine algebraic set.
. The set of all representations is denoted by R(BS(n, m)). It is not hard to verify that R (BS(n, m)) can be endowed with the structure of an affine algebraic set.
Recall that two representations p and p' are equivalent (conjugate), denoted  , if there exists
, if there exists  such that
such that  for every g
for every g  .
.
An immediate consequence of the definition above is, two representations p and p' of BS(n, m) are equivalent if and only if there exists  such that
such that  and
and .
.
The character of a representation p is the function 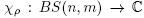 defined by
defined by . Since, equivalent representations have the same character, the map
. Since, equivalent representations have the same character, the map
where  induce a well-defined function
induce a well-defined function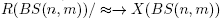 .
.
Definition 2.8. Let  . Then p is called irreducible if the only subspaces of
. Then p is called irreducible if the only subspaces of  which are invariant under p(BS(n, m)) are {0} and
which are invariant under p(BS(n, m)) are {0} and  . In other case, we say that p is reducible.
. In other case, we say that p is reducible.
From the previous definition, a representation p Є R(BS(n, m)) is reducible if and only if all p(g), with g Є BS(n, m), have a common one-dimensional eigenspace. Therefore, a representation p Є R(BS(n, m)) is reducible if and only if p(x) and p(y) have a common eigenvector.
The proof of the following theorem can be found in [9].
Theorem 2.9. Let p Є R(BS(n, m)), then p is reducible if and only if  = 2, for each element c of the commutator subgroup of BS(n, m).
= 2, for each element c of the commutator subgroup of BS(n, m).
In this case, if  denotes the image of p, then every element of the commutator subgroup
denotes the image of p, then every element of the commutator subgroup  of
of is parabolic.
is parabolic.
A representation p is abelian if its image is an abelian subgroup of SL(2,  ), and nonabelian otherwise. We denote the set of nonabelian representations of BS(n, m) by nab-rep(BS(n, m)).
), and nonabelian otherwise. We denote the set of nonabelian representations of BS(n, m) by nab-rep(BS(n, m)).
Definition 2.10. Let p Є R(BS(n,m)). Then p is called parabolic if p(y) is conjugate to D(1,1) or D(1,-1). Besides, if p(y) is conjugate to D(δ), then p is elliptic, hyperbolic or strictly loxodromic depending of the subset of C containing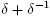 .
.
A representation 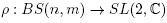 is said to be faithful if the kernel of p is trivial.
is said to be faithful if the kernel of p is trivial.
We recall the definition of residually finite groups.
Definition 2.11. A group G is called residually finite if for every g and h in G there exist a finite group F and a homomorphism y :  such that
such that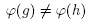 .
.
The following theorem gives us a complete classification of the Baumslag-Solitar groups in terms of the previous definition. Its proof can be found in [7].
Theorem 2.12. The group BS(m,n) is residually finite if and only if |m| = |n| or |m| = 1 or | n| = 1 .
Definition 2.13. A group G is said to be a linear group if there exists a faithful representation 
The proof of the next theorem can be found in [6].
Theorem 2.14. Let R be a field, and let M be a finite set of n by n matrices with elements in R and with non-vanishing determinant. Then the set of matrices in M generate a residually finite group.
Corollary 2.15. Linear groups are residually finite.
Therefore, BS(n, m) does not have faithful representations if |m| ≠ |n| and |m| ≠ 1 and |n| ≠ 1.
3. Non-abelian representations of BS(n, m)
In this section we will construct a collection of algebraic varieties that encode information about the set of equivalence classes of non-abelian representations of BS(n, m).
For an ideal J of , we denote by
, we denote by 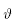 (J) the algebraic variety
(J) the algebraic variety .
.
3.1. The case BS(n, n)
Let us start this section with the following theorem.
Theorem 3.1. Let A Є SL(2,  ) be a non scalar matrix and λ = tr( A) ≠ 0. Consider the infinite sequence of polynomials in
) be a non scalar matrix and λ = tr( A) ≠ 0. Consider the infinite sequence of polynomials in , where
, where . Then
. Then
Proof. From the Cayley-Hamilton theorem . Therefore
. Therefore
Now suppose that
 . From the equation (1),
. From the equation (1),
and so
The proof of the following lemma is a direct consequence of the Cayley-Hamilton theorem, so we will omit it.
Lemma 3.2. Let A in SL(2,  ) be a non scalar matrix such that tr(A) = 0, then
) be a non scalar matrix such that tr(A) = 0, then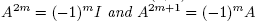 .
.
Corollary 3.3. Let A, B in SL(2,  ) be non scalar matrices such that
) be non scalar matrices such that 

Let A be a non scalar matrix with λ ≠ tr(A) ≠ 0 and . Then
. Then . Therefore A is a diagonalizable matrix, so there exists
. Therefore A is a diagonalizable matrix, so there exists  and
and  such that
such that , with,
, with,  and
and 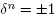 .
.
Now, let B Є SL(2,  ) be a non-scalar matrix. It is well known that AB = BA implies that B = WD(y)W-1, with y2 - 1 ≠ 0. We have proven the following theorem.
) be a non-scalar matrix. It is well known that AB = BA implies that B = WD(y)W-1, with y2 - 1 ≠ 0. We have proven the following theorem.
Theorem 3.4. Let φ be a representation of BS(n, n), with φ(x) = B and φ(y) = A non-scalar matrices, and let λ = tr(A) ≠ 0, then:
(a) If  , then A is a diagonalizable matrix. Moreover, AB = BA if and only if A and B are simultaneously diagonalizable.
, then A is a diagonalizable matrix. Moreover, AB = BA if and only if A and B are simultaneously diagonalizable.
Therefore, if φ is a non abelian representation, then A must be elliptic and
The following lemma will give us a easy way to compute the polynomial  for the case of diagonalizable matrices.
for the case of diagonalizable matrices.
Lemma 3.5.
Let
 be a non-scalar matrix, with
be a non-scalar matrix, with and
and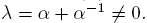 . Then,
. Then,
(a) If n is an even number, then
and
(b) ifn is a odd number, then
Proof. From Theorem 3.1,
If we multiply both sides by an, we obtain 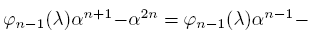
1. This implies that
The rest of the proof follows by factorizing polynomials of the form
Theorem 3.6. With the notation above.
(1) If n is a even number, then there exists an injective function from the algebraic set  (J) into nab-rep(BS(n,n))/ ≈, where J is the ideal of
(J) into nab-rep(BS(n,n))/ ≈, where J is the ideal of  spanned by
spanned by
(2) If n is an odd number, then there exists an injective function from the algebraic set  (J) into nab-rep(BS(n,n))/ ≈, where J is the ideal of
(J) into nab-rep(BS(n,n))/ ≈, where J is the ideal of spanned by
spanned by
Proof. (1) Let  and let
and let 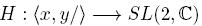 the canonical homomorphism such that H(x) = D(y, β) and H(y) = D(α). Suppose that n = 2t, t > 0.
the canonical homomorphism such that H(x) = D(y, β) and H(y) = D(α). Suppose that n = 2t, t > 0.
Now, consider the following two cases for the trace, A, of D(a).
Case 2: if λ ≠ 0, then  Therefore
Therefore 
From the previous cases, and the fact that H(x) and H(y) are not simultaneously diagonalizable, H extends to a nonabelian representation 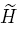 . So, we can define the function
. So, we can define the function
where  is the equivalence class of the representation
is the equivalence class of the representation  .
.
Let  be such that
be such that 
 then there exists
then there exists  and
and 
By expanding the matrix equality  we obtain two possibilities, either
we obtain two possibilities, either  If we suppose that
If we suppose that  then C11 = C22 = 0 and C21 =
then C11 = C22 = 0 and C21 =  If we replace them in the equation CD(x
3, x
2)C
-1 = D(y
3, y
2), we get that C
12 = 0, but this is a contradiction, and so x
1 = y
1, and therefore C = I. Hence, ç is an injective function.
If we replace them in the equation CD(x
3, x
2)C
-1 = D(y
3, y
2), we get that C
12 = 0, but this is a contradiction, and so x
1 = y
1, and therefore C = I. Hence, ç is an injective function.
(2) Let (α, β,Υ ,σ) Є 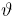 (J) and let, again, H :
(J) and let, again, H : 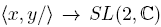 be the canonical homomorphism given by H(y) = D(α) and H(x) = D(Υ, β).
be the canonical homomorphism given by H(y) = D(α) and H(x) = D(Υ, β).
Because g(α, β,Υ ,σ) = 0, then 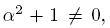 therefore
therefore  and, from Lemma 3.5,
and, from Lemma 3.5,  Therefore H extends to a non-abelian representation
Therefore H extends to a non-abelian representation  . So, we can define the function
. So, we can define the function
where  is the equivalence class of the representation
is the equivalence class of the representation 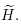
The proof that ç is an injective function is quite similar to what we did in the proof of (1). 
We conclude this section with the fact that for every  all the representations in the equivalence class
all the representations in the equivalence class  are reducible.
are reducible.
Theorem 3.7.
Every representation in
 is reducible.
is reducible.
Proof.
Let  be the representative element of
be the representative element of 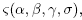 where
where 
 and
and  The eigenspace
The eigenspace  corresponds to the eigenvalue α-1, of the matrix
corresponds to the eigenvalue α-1, of the matrix  (y), and has the property that it is an eigenspace of the matrix
(y), and has the property that it is an eigenspace of the matrix  (x). Therefore
(x). Therefore  is an
is an  (BS(n, n))-invariant subspace of
(BS(n, n))-invariant subspace of 

3.2. The case BS(n,m), with n ≠ m
We start this section with the following theorem.
Theorem 3.8. There are no non-abelian representations  of BS(n,m) such that
of BS(n,m) such that (x) and
(x) and  (y) are both parabolic matrices.
(y) are both parabolic matrices.
Proof. Suppose that there exists a non-abelian representations  of BS(n,m) in which
of BS(n,m) in which  (x) and
(x) and  (y) are both parabolic matrices. Then
(y) are both parabolic matrices. Then  is a conjugate of the non-abelian representations
is a conjugate of the non-abelian representations  such that
such that 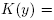

Then we prove that (2) is true if and only if w12 = 0 and  . Since
. Since  then
then  and so
and so  Hence,
Hence, 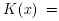
 where
where  and
and 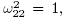 , that is a contradiction.
, that is a contradiction.
Corollary 3.9. Let  m and denote by L the ideal of
m and denote by L the ideal of spanned by f (z, w). Then there exists a function from the algebraic variety
spanned by f (z, w). Then there exists a function from the algebraic variety (L) into nab-rep(BS(n, m))/ ≠.
(L) into nab-rep(BS(n, m))/ ≠.
Proof. Let  and consider the map
and consider the map
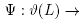
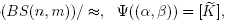
where  is the representation given by
is the representation given by  =
=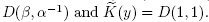 It is not hard to prove that Ψ is a well-defined function.
It is not hard to prove that Ψ is a well-defined function.  The function Ψ is not injective because
The function Ψ is not injective because 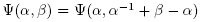 and
and 
Theorem 3.10. With the above notation. The representation 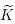 is reducible.
is reducible.
Proof.
Consider the eigenspace  . Then, E is a K(BS(n, m))-invariant one dimensional subspace of
. Then, E is a K(BS(n, m))-invariant one dimensional subspace of 

Theorem 3.11. If 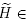 nab-rep(BS(n, m)) and
nab-rep(BS(n, m)) and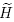 (y) is not a parabolic matrix, then
(y) is not a parabolic matrix, then 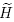 (y) has finite order.
(y) has finite order.
Proof. Suppose that  nab-rep(BS(n, m)) and
nab-rep(BS(n, m)) and  (y) is not a parabolic matrix. Then
(y) is not a parabolic matrix. Then  must be equivalent to a representation
must be equivalent to a representation , such that
, such that 
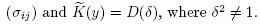
The matrix equality  is true if and only if
is true if and only if
Now, 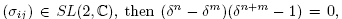 therefore D (δ) is an elliptic matrix of finite order. Moreover, since
therefore D (δ) is an elliptic matrix of finite order. Moreover, since  is a non abelian representation, then we have to add one of the following inequalities
is a non abelian representation, then we have to add one of the following inequalities 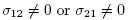 …………………………………………….
…………………………………………….
Theorem 3.12. We suppose that m > n. Let g1(α, β, Υ, σ)  ,
, and let I the ideal of
and let I the ideal of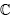 [α, β, Υ, σ] spanned by {g
1
, g
2
}. Then, there exist a injective function from the algebraic variety
[α, β, Υ, σ] spanned by {g
1
, g
2
}. Then, there exist a injective function from the algebraic variety (I) into nab-rep(BS(n, m)) .
(I) into nab-rep(BS(n, m)) .
Proof. Consider the map
 nab-rep(BS(n,m)),
nab-rep(BS(n,m)),  where
where 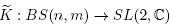 is the representation given by
is the representation given by 
Due to the fact that 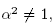 and from Theorem 3.11, we get that
and from Theorem 3.11, we get that  is a non-abelian representation, therefore we have shown that
is a non-abelian representation, therefore we have shown that  is well defined.
is well defined.
The proof that  is an injective function, is straightforward.
is an injective function, is straightforward. 
4. On non-abelian faithful representations of BS(n,m)
From the Theorem 2.12, the group BS(n, m) could have a non-abelian faithful representation in SL(2,  ) only for the cases in which n = m or n = 1 or m = 1. But, we know that BS(n,n) does not have non-abelian faithful representations into SL(2,
) only for the cases in which n = m or n = 1 or m = 1. But, we know that BS(n,n) does not have non-abelian faithful representations into SL(2,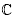 ). (see Theorem 3.6). Therefore there only remains the case n = 1, because for m =1 we have that BS(1, m)
). (see Theorem 3.6). Therefore there only remains the case n = 1, because for m =1 we have that BS(1, m) 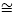 BS(m, 1).
BS(m, 1).
Before the proof that BS(1,m) is a linear group, consider the following theorem.
Theorem 4.1.
Each element
 Є BS(1, m) is uniquely represented by a word of the form
Є BS(1, m) is uniquely represented by a word of the form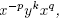 where p, k, q are integers and p, q
where p, k, q are integers and p, q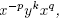 0.
0.
Proof.
From  we obtain the infinite family of relators {
we obtain the infinite family of relators { 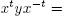
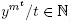 }. So, we have the following four kinds of equations:
}. So, we have the following four kinds of equations:
Without loss of generality, we may suppose that the words in BS(1,m) have the form  where
where  We will complete the proof by induction on the length n.
We will complete the proof by induction on the length n.
When n = 1, then 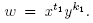 So, if t1 > 0, then from (a) and (d),
So, if t1 > 0, then from (a) and (d), 
Now assume that  . then
. then  . By the induction hypothesis
. By the induction hypothesis 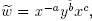 where a, c ≥ 0, so w =
where a, c ≥ 0, so w = 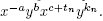 If c + tn ≥ 0, from (a) and (d),
If c + tn ≥ 0, from (a) and (d),  , but if c + tn ≤ 0, from (b) and (c),
, but if c + tn ≤ 0, from (b) and (c), 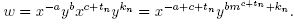

Corollary 4.2. Let m £ Z such that |m| > 1, then BS(1, m) is a linear group, and it is residually finite.
Proof. We give the proof for the case m > 1. From Theorem 3.8, there exists a representation  : BS(1,m)
: BS(1,m)  SL(2,
SL(2, 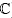 ), such that
), such that  (x) = D(m-1/2) and
(x) = D(m-1/2) and  (y) = D(1 , 1).
(y) = D(1 , 1).
Let w be a word in BS(1 ,m) such that  (w) = I. Because w is uniquely represented by a word of the form
(w) = I. Because w is uniquely represented by a word of the form 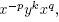 where
where  and p, q ≥ 0, then
and p, q ≥ 0, then
hence,  (w) = I if and only if p = q and k = 0. Therefore w =1 and so
(w) = I if and only if p = q and k = 0. Therefore w =1 and so  is injective.
is injective. 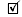
If m = -1, then we have that D2(δ, i) = D(-1), therefore D(δ, i) is a matrix of order 4, as a consequence, neither of the representations given in the proof of Theorem 3.8 are faithful.
Let  and
and  where A = D(1,1) and B = D(m-1/2). Let
where A = D(1,1) and B = D(m-1/2). Let  , with m > 1, be the subgroup of
, with m > 1, be the subgroup of  generated by
generated by  and
and 
Proposition 4.3. The subgroup 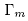 is an elementary subgroup of
is an elementary subgroup of  . Moreover,
. Moreover,  is not a Fuchsian group.
is not a Fuchsian group.
therefore, from Theorem 2.7 we have that 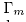 is an elementary subgroup of
is an elementary subgroup of 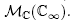 . Besides,
. Besides, 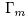 is not abelian, and hence it is not cyclic. Since A is not a diagonalizable matrix,
is not abelian, and hence it is not cyclic. Since A is not a diagonalizable matrix, 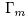 is not conjugate to some group of the form
is not conjugate to some group of the form 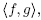 where g(z) = kz (k > 1) and f (z) =-1/z -then
where g(z) = kz (k > 1) and f (z) =-1/z -then 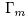 is not a Fuchsian group.
is not a Fuchsian group. 
Theorem 4.4.
The subgroup
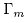 is not discrete.
is not discrete.
Proof.
Let  then there exists p, q, k in
then there exists p, q, k in  with p, q ≥ 0 such that
with p, q ≥ 0 such that 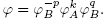 Due to the fact that
Due to the fact that
Then
If we take t = 3 and p = q, then the previous inequality becomes 2m2p + k2 ≤ 3m2p, and so k2 ≤ m2p. It is not hard to prove that there are infinitely many pairs (k,p) G  such that k2 ≤ m2p.
such that k2 ≤ m2p.