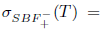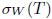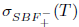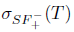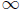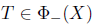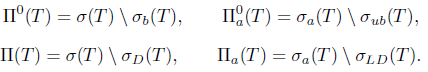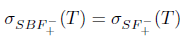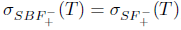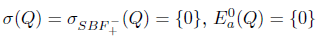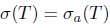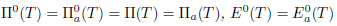English (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
1. Introduction and preliminaries
In this paper, we introduce two new spectral properties type Weyl-Browder theorems, namely the properties (Saw) and (Sab), respectively. In addition, we establish the precise relationships between these properties and others variants of Weyl's and Browder's theorem that have been recently introduced in [10,14,17,18,22,25] and [27].
Throughout this paper, L(X) denotes the algebra of all bounded linear operators acting on an infinite-dimensional complex Banach space X. We refer to [24] for details about notations and terminologies. However, we give the following notations that will be useful in the sequel:
Browder spectrum:
Weyl spectrum
Upper semi-Browder spectrum
Upper semi-Weyl spectrum
Left Drazin invertible spectrum
Drazin invertible spectrum
B-Weyl spectrum
Upper semi-B-Weyl spectrum
Lower semi-B-Weyl spectrum
approximate point spectrum
surjectivity spectrum
.
Recall that an operator 
is said to have the single valued extension property at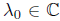 
(abbreviated SVEP at λ0) if for every open disc 
centered at λ0 the only analytic function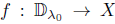 
which satisfies the equation
is 
(see [16]). The operator T is said to have SVEP if it has SVEP at every point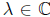 
. Evidently, every 
has SVEP at each point of the resolvent set 
. Moreover, Τ has SVEP at every point of the boundary 
of the spectrum. In particular, Τ has SVEP at every isolated point of the spectrum. Note that (see [1, Theorem 3.8])
and dually
It is easily seen from definition of localized SVEP that
where acc K means the set of all accumulation points of 
, and
Remark 1.1. The implications (1)-(4) are actually equivalences whenever λΙ- Τ is a quasi-Fredholm operator, in particular when λΙ - Τ is semi B-Fredholm (see [2]).
Lemma 1.2. ([3, Lemma 2.4]) Let Τ G L(X). Then
(i) Τ is upper semi B-Fredholm and
(Τ) <
if and only if
.
(ii) Τ is lower semi B-Fredholm and β(Τ) <
.
The following lemma is a particular case of [9, Theorem 3.6].
Lemma 1.3. For Τ 
L(X), the following statements are equivalent:
(i) λ0 Ι - Τ is left Drazin invertible ·
· λ0 Ι - Τ is quasi-Fredholm with finite ascent,
(ii) λ0 Ι - Τ is right Drazin invertible ·
(iii) λ0 Ι-Τ is Drazin invertible ·
Denote by iso K, the set of all isolated points of 
define
Also, define
Let 
. Following Coburn [15], Τ is said to satisfy Weyl's theorem, in symbols (
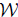), if 
. Following Rakocevic ([20],[19]), Τ is said to satisfy 
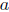-Weyl's theorem, in symbols (
), if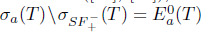 
, and Τ is said to have property (w) if 
. According to Berkani and Koliha [11], Τ is said to satisfy generalized Weyl's theorem, in symbols 
. Similarly, Τ is said to satisfy generalized a-Weyl's theorem, in symbol 
.
Now, we describe several spectral properties introduced recently in [7,10,13,14,17,18,22,23,25,26] and [27].
Definition 1.4. An operator Τ 
L(X) is said to have:
(i) property (gw) [7] if
.
(ii) property (b) [13] if
.
(iii) property (gb) [13] if
.
(iv) property (aw) [14] if
.
(v) property (gaw) [14] if
.
(vi) property (ab) [14] if 
.
(vii) property (gab) [14] if
.
(viii) property (z) [25] if
.
(ix) property (gz) [25] if
.
(x) property (az) [25] if
.
(xi) property (gaz) [25] if
.
(xii) property (ah) [26] if
.
(xiii) property (gah) [26] if
.
(xiv) property (Bw) [17] if
.
(xv) property (Baw) [27] if
.
(xvi) property (Bgw) [22] if
.
(xvii) property (Bab) [27] if
.
(xviii) property (Bb) [22] if
.
(xix) property (Bgb) [22] if
.
(xx) property (SBaw) [10] if
.
(xxi) property (SBab) [10] if
.
(xxii) property (Sw) [23] if
.
(xxiii) property (Sb) [23] if
.
The properties (Bgw) and (Bgb) are also called (SBw) and (SBb), respectively (see [10]). Property ( Bb) was also introduced in [18].
2. Properties (Saw) and (Sab).
According to [24], Τ 
L(X) has property (gv) (resp. (v)) if 
(resp. 
and it was proved in [24, Corollary 2.12], that property (gv) (resp. (v)) is equivalent to property (gz) (resp. (z)). Property (gv) (resp. (v)) also is called property (gt) (resp. (t)) in [21] and property (gh) (resp. (h)) in [26]. In this section we introduce and study two new spectral properties that are independent of property (gv) (and hence of property (gz)).
Definition 2.1. An operator ΤL(X) is said to have property (Saw) if 
, and property (Sab) if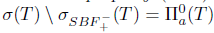 
.
The next result gives the precise relationship between the properties (Saw) and (z).
Theorem 2.2. For Τ L(X), the following statements are equivalent:
(i) Τ has property (Saw),
(ii) Τ has property (z) and
,
(iii) Τ has property (v) and
.
Proof. (i) 
(ii) Assume that Τ satisfies property (Saw) and let λ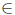 
σ(Τ) \ 
. Since 
, we have λ 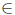σ(Τ) \ 
. As Τ satisfies property (Saw), it follows that λ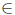
. This shows 
.
To show the opposite inclusion 
.
Then 
and 
. Since Τ satisfies property (Saw), we have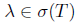 
and λΙ - Τ is upper semi-B-Weyl. Thus, λΙ - Τ is an upper semi B-Fredholm operator and 
. By Lemma 1.2, we have that λΙ - Τ is an upper semi-Fredholm operator, so λΙ - Τ is an upper semi-Weyl operator. Hence, 
and so 
. This shows that Τ satisfies property (z). Consequently,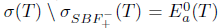 
and 
. Therefore,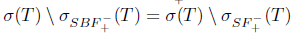 
.
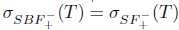(ii) 
(i). Suppose that Τ satisfies property (z) and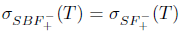 
.
Then,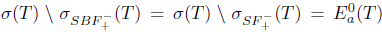 
, and hence Τ satisfies property (Saw).
(ii) 
(iii). The equivalence between properties (z) and (v) has been proved in [24, Corollary 2.12]. 
From Theorem 2.2, we observe that property (Saw) implies property (z). But the converse of this implication does not hold in general, as we can see in the following example.
Example 2.3. Let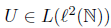 
be defined by
Then, 
. In consequence
Hence, Τ satisfies property (z), but not property (Saw).
Similarly to Theorem 2.2, we have the following result.
Theorem 2.4. For Τ 
L(X), the following statements are equivalent:
(i) Τ has property (Sab),
(ii) Τ has property (az) and
,
(iii) Τ has property (gaz) and
.
Proof. The proof (i) 
(ii), is similar to the proof (i) (ii) of Theorem 2.2. The proof (ii) (iii), follows of the equivalence between properties (az) and (gaz) proved in [25, Corollary 3.5].
From Theorem 2.4, we note that property (Sab) implies property (az). But the converse is not true in general as shown by the following example.
Example 2.5. Consider the operator T = 0 defined on the Hilbert space 
.
Then, 
. Therefore, 
and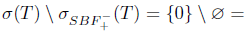 
. Thus, T satisfies property (az), but not property (Sab).
The next result gives the relationship between the properties (Saw) and (SB aw).
Theorem 2.6. Let T 
L(X). Then T has property (Saw) if and only if T has property (SBaw) and
.
Proof. Sufficiency: Assume that T satisfies property (Saw) and 
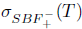. Since 
, we have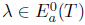 
and so, 
.
To show the opposite inclusion 
. Then, 
and since T satisfies property (Saw), it follows that 
and so, 
. Hence, 
and T satisfies property (SBaw). Consequently, 
and 
. Therefore, 
and 
.
Necessity: Assume that T satisfies property (SBaw) and 
. Then, 
. Thus, 
and T satisfies property (Saw). 
Similarly to Theorem 2.6, we have the following result.
Theorem 2.7. Let T 
L(X). Then T has property (Sab) if and only if T has property (SBab) and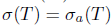
.
Proof. The proof is similar to the proof of Theorem 2.6.
The next example shows that, in general, property (SBaw) (resp. (SBab)) does not imply property ( Saw) (resp. ( Sab)).
Example 2.8. Let R be the unilateral right shift operator on 
and U be the operator defined in Example 2.3. Define an operator T on 
by 
. Then,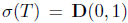 
, the closed unit disc on 
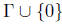, where Γ denotes the unit circle of 
and 
. Moreover, 
and 
. Therefore, 
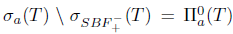. Thus, T satisfies both properties (SBaw) and (SBab). On the other hand, 
and 
. Therefore, T does not satisfy property (Saw) or property (Sab).
Corollary 2.9. Let T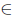 
L(X). Then:
(i) T has property ( Saw) if and only if T has property (Sw).
(ii) T has property ( Sab) if and only if T has property (Sb).
Proof.
(i) Suppose that T satisfies property (Saw). By Theorem 2.6
and so, 
. Therefore, T satisfies property ( Sw).
Conversely, assume that T satisfies property (Sw). By [23, Theorem 2.25], 
and so, 
. Therefore, T satisfies property (Saw).
(ii) The proof is similar to the proof of (i). Just use both Theorem 2.7 and [23, Theorem 2.28].
The next result gives the relationship between the properties (Saw) and ( Baw).
Theorem 2.10. Let T 
L(X). Then T has property (Saw) if and only if T has property (Baw) and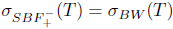
.
Proof. Sufficiency: Suppose that T satisfies property (Saw), that is 
, then λI - T is a B-Weyl operator, and hence it is upper semi-B-Weyl. Thus 
, and
so 
.
To show the opposite inclusion 
. Since T satisfies property (Saw), λ 
iso 
and λI - T is an upper semi-B-Predholm operator, hence quasi-Predholm. By Theorem 2.6, λ 
iso 
, it follows that both T and T* have SVEP in λ, and by Remark 1.1, 0 < 
. Prom Lemma 1.3, we have λI - T is a Drazin invertible operator, and hence it is B-Weyl. Therefore, 
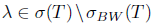, and so 
. This shows that T satisfies property (Baw). Consequently,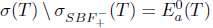 
and 
. Therefore, 
.
Necessity: Suppose that T satisfies property (Baw) and 
. Then,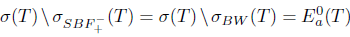 
, and so T satisfies property (Saw). 
Similarly to Theorem 2.10, we have the following result.
Theorem 2.11. Let T L(X). Then T has property (Sab) if and only if T has property (Bab) and
.
Proof. The proof is similar to the proof of Theorem 2.10. 
The next example shows that, in general, property (Baw) (resp. (Bab)) does not imply property (Saw) (resp. (Sab)).
Example 2.12. Let R be the unilateral right shift operator on 
. Define an operator T on 
. Then, 
, 
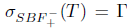. Moreover, 
.
Therefore, 
. Thus, T satisfies property (Baw) and hence property (Bab), but not property (Saw) or property ( Sab).
The next result gives the relationship between the properties (Saw) and (aw).
Theorem 2.13. Let T 
L(X). Then T has property (Saw) if and only if T has property (aw) and
.
Proof. Sufficiency: Assume that T satisfies property (Saw); then it also satisfies property (Baw) by Theorem 2.10. Property (Baw) implies by [27, Theorem 3.3] that T satisfies property (aw). Consequently, 
and 
. Therefore, 
.
Necessity: Suppose that T satisfies property (aw) and 
. Then, 
, and hence T satisfies property ( Saw). 
Similarly to Theorem 2.13, we have the following result.
Theorem 2.14. Let T 
L(X). Then T has property (Sab) if and only if T has property (ab) and
.
Proof. The proof is similar to the proof of Theorem 2.13. Just use both Theorem 2.11 and [27, Theorem 3.6]. 
The next example shows that, in general, property ( aw) (resp. (ab)) does not imply property (Saw) (resp. ( Sab)).
Example 2.15. Let R be the unilateral right shift operator on 
. Then, 
. Moreover, 
and 
. Therefore, 
and 
. Thus, R satisfies property (aw) and hence property (ab), but not property (Saw) or property (Sab).
As a consequences of the results above, we have the following two corollaries, where we give new characterizations of the properties (Sw) and (Sb), respectively.
Corollary 2.16. For T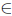 
L(X), the following statements are equivalent:
(i) T has property (Sw),
(ii) T has property (z) and
·
(iii) T has property (v) and
·
(iv) T has property (SBab) and
·
(v) T has property (Bab) and
(vi) T has property (aw) and
·
Corollary 2.17. For T 
L(X), the following statements are equivalent:
(i) T has property (Sb),
(ii) T has property (az) and
·
(iii) T has property (gaz) and
·
(iv) T has property (SBab) and
·
(v) T has property (Bab) and
·
(vi) T has property (ab) and
·
Recall that T 
L(X) is said to satisfy a-Browder's theorem (resp. generalized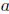
-Browder's theorem) if 
(resp.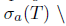 
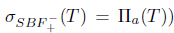. From [8, Theorem 2.2] (see also [4, Theorem 3.2(ii)]), 
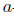-Browder's theorem and generalized a-Browder's theorem are equivalent. It is well known that a-Browder's theorem for T implies Browder's theorem for T, 
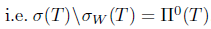. Also by [8, Theorem 2.1], Browder's theorem for T is equivalent to generalized Browder's theorem for 
.
The next result gives the relationship between the properties (Saw) and (Sab).
Theorem 2.18. Let T 
L(X). Then T has property (Saw) if and only if T has property (Sab) and
.
Proof. Sufficiency: Assume that T satisfies property (Saw); then it satisfies property (SBaw), by Theorem 2.6. Property (SBaw) implies by [10, Theorem 2.12] that T satisfies a-Weyl's theorem, o equivalently T satisfies a-Browder's theorem and 
[5, Theorem 2.14]. Since that T satisfies property (Saw), it follows that 
, and hence 
.
Necessity: Suppose that T satisfies property (Sab) and 
. Then 
and so T satisfies property (Saw). 
The next example shows that property (Sab) does not imply property (Saw).
Example 2.19. Consider 
defined as
Then, 
and 
. We thus have
Hence, T satisfies property (Sab), but not property (Saw).
Corollary 2.20. For T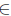 
L(X), the following statements are equivalent:
(i) T has property (Saw),
(ii) T has properties (Sab) and (SBaw).
(iii) T has property (Sab) and satisfies a-Weyl's theorem.
Proof.
Follows immediately from the proof of Theorem 2.18. 
The following two examples show that the properties (Saw) (resp. (Sab)) and (gv) (or (gz)) are independient.
Example 2.21. Consider the operator T defined in Example 2.5. Then, 
, and hence T does not satisfy property (Saw) or property (Sab). Moreover, we have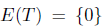 
. Consequently, 
and so, T satisfies property (gv).
Example 2.22. Let Q be defined for each 
by
where (
) is a sequence of complex numbers such that 
and 
. It follows from [11, Example 3.12], that
·Define the operator T on 
. Then, 
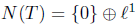
. Since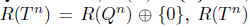 
is not closed for any n 
N; so T is not an upper semi B-Weyl operator and - 
. We then have,
Hence, T satisfies property (Saw) and hence property (Sab), but does not satisfy property ( gv).
In the next theorem we give a new characterization of operators having property ( Sb).
Theorem 2.23. Let T 
L(X). Then T has property (Sb) if and only if T has (Bb) and ind 
for all 
.
Proof. Sufficiency: Assume that T satisfies property (Sb); then it also satisfies property (Bb), by [23, Theorem 2.6]. Let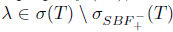 
, as T satisfies property (Sb), then 
. Thus 
and 
.
Necessity: Suppose that T satisfies property (Bb) and ind for all 
, then 
is an upper semi-B-Fredholm operator with ind 
, it follows that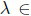 
, and as T satisfied property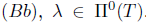 
. This shows 
. Conversely, let 
. Then 
and hence 
. Thus, 
and T satisfies property (Sb). 
Corollary 2.24. For T 
L(X), the following statements are equivalent:
(i) T has property (Saw),
(ii) T has property (Sb) and
,
(iii) T has property (Bgw) and
,
(iv) T has property (Bw) and
Proof. The equivalence (i) 
(ii) follows immediately from Theorem 2.18 and Corollary 2.9. The equivalence (i) (iii) follows immediately from Corollary 2.9 and [23, Theorem 2.25]. The equivalence (i) (iv) follows immediately from Corollary 2.9 and [23, Theorem 2.8]. 
Similarly to Corollary 2.24, we have the following result.
Corollary 2.25. For T 
L(X), the following statements are equivalent:
(i) T has property ( Sab),
(ii) T has property (Bgb) and
,
(iii) T has property (Bb) and
.
Proof. The equivalence (i) 
(ii) follows immediately from Corollary 2.9 and [23, Theorem 2.8]. The equivalence (i) (iii) follows immediately from Corollary 2.9 and Theorem 2.23. 
Theorem 2.26. Suppose that T G L(X) has property (Saw). Then:
(i) T satisfies generalized a-Browder's theorem and
.
(ii) T satisfies generalized Browder's theorem and
.
Proof. (i) By [6, Theorem 2.4], it is sufficient to prove that T has SVEP at every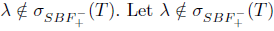 
. We have the following two cases.
Case 1. 
Case 2. 
.
In Case 1, clearly T has SVEP at λ. In Case 2, we have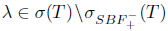 
and since T satisfies property (Saw), it follows that 
. Therefore, 
and so T has SVEP at λ again.
To show the equality 
, observe first that 
holds for every T
L(X). To show the opposite inclusion, suppose that 
and 
. Then 
, since T satisfies property (Saw). Therefore, 
, and so 
. This shows that 
.
(ii) Follows from (i), by using the fact that generalized a-Browder's theorem implies generalized Browder's theorem, and the equality
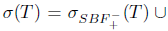
, implies the inclusion
, leading to
.
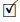
For T 
L(X), define 
. The precise relationship between generalized a-Browder's theorem and property (Saw) is described by the following theorem.
Theorem 2.27. For T 
L(X), the following statements are equivalent:
(i) T has property (Saw),
(ii) T satisfies generalized a-Browder's theorem and
.
Proof. (i) 
(ii) Assume that T satisfies property (Saw). Then, by Theorem 2.26, it is sufficient to prove 
. Indeed,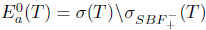 
, since T satisfies property (Saw) and generalized 
-Browder's theorem by Theorem 2.27.
(ii) 
(i) If T satisfies generalized 
-Browder's theorem and 
, then 
. Therefore, T satisfies property (Saw). 
Corollary 2.28. If T 
L(X) has SVEP at each
, then T has property (Saw) if and only if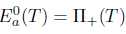 
.
Proof. The hypothesis T has SVEP at each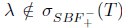 
, implies that T satisfies generalized a-Browder's theorem. Therefore, if 
, then 
Remark 2.29. It was proved in [12, Lemma 2.4], that if T* has SVEP at every 
(resp. T has SVEP at every 
, then 
and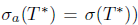 
. Under the above results, clearly we have that if T* has SVEP at every 
(resp. T has SVEP at every 
, then the properties (Bw), (Sw), (Saw), (Bgw), (Baw) and (SBaw) are equivalent for T (resp. for T* ). In the same form, we obtain equivalence for the properties (Bb), (Sb), (Sab), ( Bgb), (Bab) and (SBab).
Theorem 2.30. Suppose that T 
L(X) has property property (Saw). Then:
(i)
(ii)
(iii) The properties (SBaw), (SBab), (Bgw), (Bgb), (w), (b), (gb), (z), (az), (gaz), (v), (ah), (gah), (Baw), (Bab), (gab), (Bw), (Bb), (aw), (ab), (
), (a
) and (a
(iv) The properties (gw), (gz), (gv), (gaw), (g
Proof. (i) By Theorem 2.6, the equality σ(Τ) = σα(Τ) holds. The equalities 
follows from Theorems 2.2, 2.10 and 2.13. Since the inclusions 
and 
hold, it is sufficient to prove 
. Indeed, 
, since Τ satisfies property (Saw) and generalized Browder's theorem or equivalently Browder's theorem, by Theorem 2.27.
(ii) The equalities 
and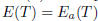 
follows from (i). By Theorem 2.18, the equality 
holds.
(iii) By Theorem 2.2, Τ satisfies property (z), and the equivalence between all properties follows from (i) and (ii).
(iv) Follows from (i) and (ii). 
Similarly to Theorem 2.30, we have the following result.
Theorem 2.31. Suppose that Τ 
L(X) has property (Sab). Then:
(i)
(ii)
and
.
(iii) The properties (SBab), (Bgb), (b), (gb), (az), (gaz), (ah), (gah), (Bab), (gab), (Bb), (ab), (
), (
), (
) and (
) for Τ are equivalent, and Τ satisfies each of these properties.
(iv) The properties (SB
w), (Bgw), (w), (z), (v), (B
) and (
(v) The properties (gw), (gz), (gv), (gaw), (gW) and (g
) for Τ are equivalent.
In the following diagram arrows mean implications between the properties defined above. The numbers near the arrows are references to the results in the present paper (numbers without brackets) or to the bibliography therein (numbers in square brackets).
