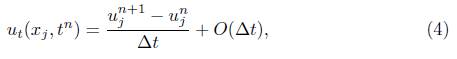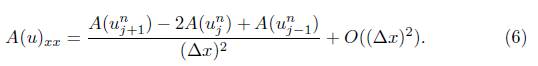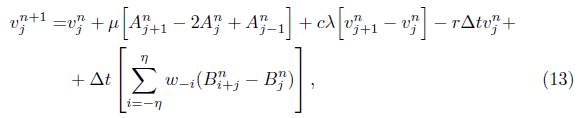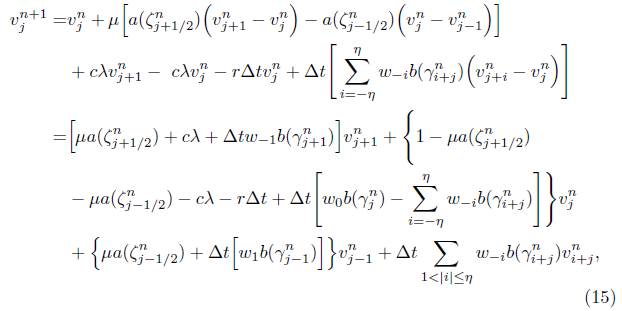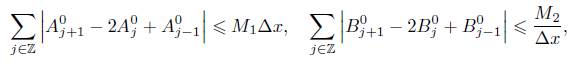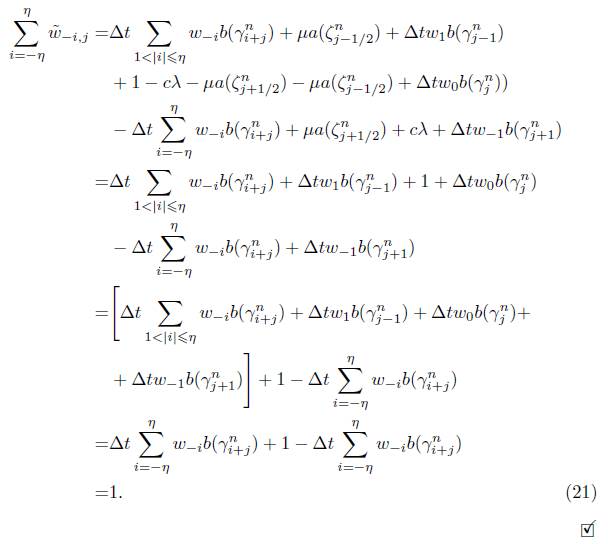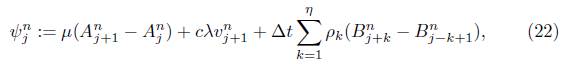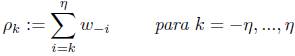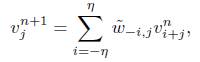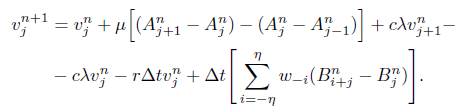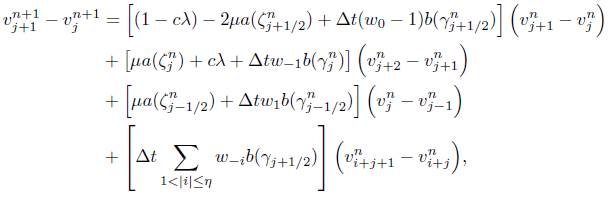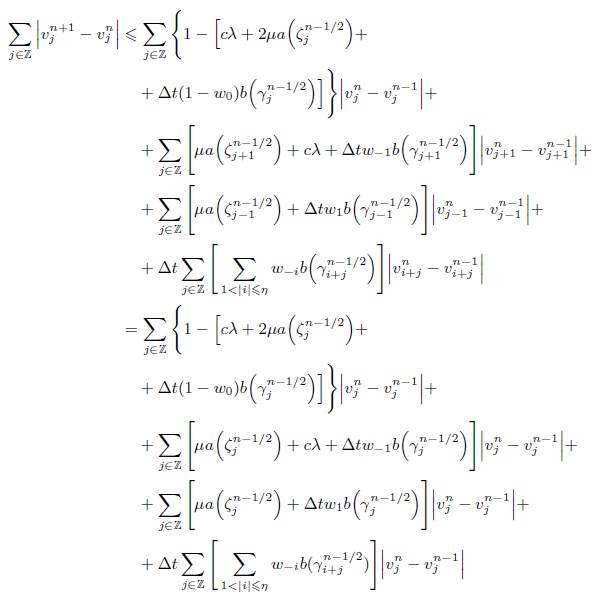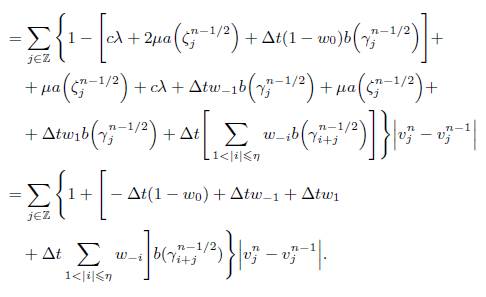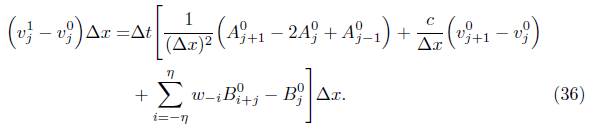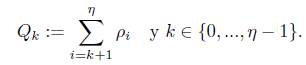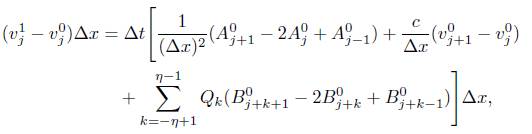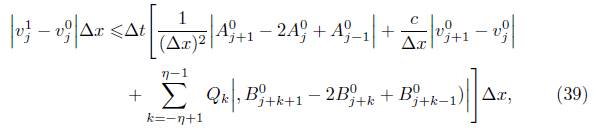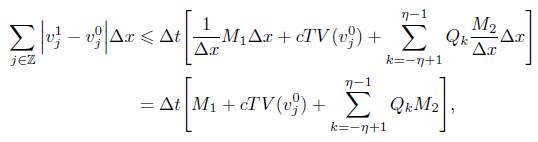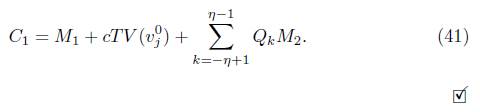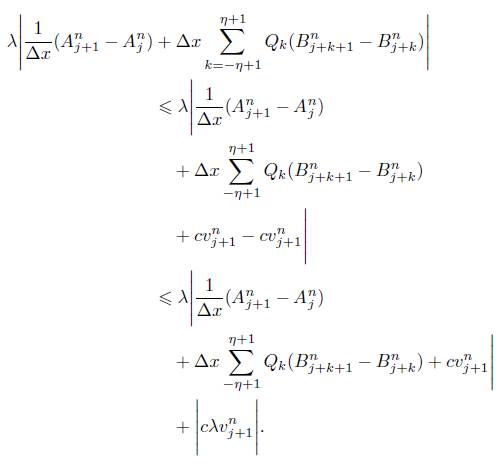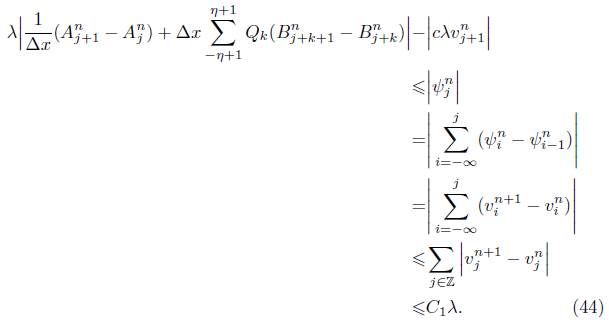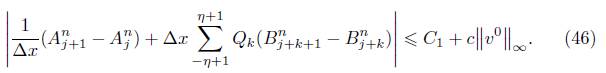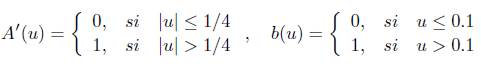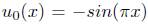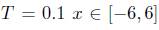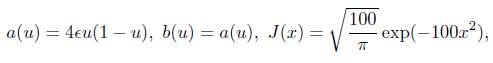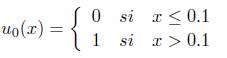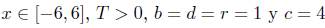1. Introducción
Nos interesa realizar la aproximación de la solución a una ecuación diferencial parcial tipo parabólica asociada al modelo de Black-Scholes (ver [7]), la cual tiene importantes aplicaciones en finanzas. Nuestro modelo viene dado por:
con  un dominio suave y acotado, T > 0, y
un dominio suave y acotado, T > 0, y  y
y  funciones suaves y a, b funciones no negativas y acotadas en todo su dominio. En este modelo consideramos r
funciones suaves y a, b funciones no negativas y acotadas en todo su dominio. En este modelo consideramos r 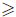 0 representando la tasa de interés libre,
0 representando la tasa de interés libre, 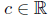 la desviación de tasa y u(x, t) la opción de precio (credito contingente). El efecto de los vecinos cercanos x y s se describe por medio de
la desviación de tasa y u(x, t) la opción de precio (credito contingente). El efecto de los vecinos cercanos x y s se describe por medio de  una función suave, no negativa, simétrica, que decae en los límites y tal que
una función suave, no negativa, simétrica, que decae en los límites y tal que  . A la función J anterior se la denomina kernel. En este artículo trabajamos con funciones kernel que sean estrictamente positivas en un intervalo (-p,p) para algún
. A la función J anterior se la denomina kernel. En este artículo trabajamos con funciones kernel que sean estrictamente positivas en un intervalo (-p,p) para algún  para
para 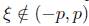 .
.
La ecuación (1) surge como una variación del modelo de Black-Scholes lineal y no nocal estudiado recientemente en [6] y [5] desde el punto de vista numérico, y considerando  . Mas especificamente, en [5] se usó una discretización basada en los métodos de diferencias finitas y molificación discreta, se obtuvo una condición CFL, y se probó que el esquema cumple propiedades importantes tales como regularidad, variación total decreciente (TVD) y demás. Por otro lado, en [6] se implementó un método multigrid para acelerar los algoritmos allí planteados. En estos artículos, se asume que la condición inicial u0 se encuentra en
. Mas especificamente, en [5] se usó una discretización basada en los métodos de diferencias finitas y molificación discreta, se obtuvo una condición CFL, y se probó que el esquema cumple propiedades importantes tales como regularidad, variación total decreciente (TVD) y demás. Por otro lado, en [6] se implementó un método multigrid para acelerar los algoritmos allí planteados. En estos artículos, se asume que la condición inicial u0 se encuentra en 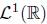 y que una solución u también esto en
y que una solución u también esto en 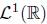 y es Lipschitziana con respecto a la primera variable en casi todas partes. Al igual que en [6] y [5], en el presente artículo hacemos las mismas consideraciones sobre u
0 y u. Además, asumimos que tanto A(s) como B(s) son funciones Lipschitzianas.
y es Lipschitziana con respecto a la primera variable en casi todas partes. Al igual que en [6] y [5], en el presente artículo hacemos las mismas consideraciones sobre u
0 y u. Además, asumimos que tanto A(s) como B(s) son funciones Lipschitzianas.
Respecto a lo teórico, la ecuación (1) ha sido estudiada desde este punto de vista en [9], [8] y [10] para los casos en los que  , donde se estudiaron la existencia, la unicidad y el comportamiento asintótico de las soluciones.
, donde se estudiaron la existencia, la unicidad y el comportamiento asintótico de las soluciones.
En cuanto al método de molificación discreta (ver [2,3,4] y [11]), este es un procedimiento de filtrado basado en convolución, que es una forma simple y efectiva para estabilizar esquemas explícitos para ecuaciones diferenciales (ver [1]). En [5] se implementó este método para realizar la aproximación numérica de la integral que figura en el esquema allí propuesto.
Como se puede evidenciar, los estudios sobre el modelo lineal y no local de Black-Scholes son amplios; sin embargo, el tratamiento numérico de modelos no locales y no lineales para dicha ecuación son casi nulos. Nuestro objetivo con este artículo es desarrollar un método numérico que aproxime en forma eficiente soluciones al modelo no local y no lineal de Black-Scholes y empezar a sentar bases para estudios que vayan cada vez más ajustados a la realidad.
Para ello, iniciamos nuestro estudio aproximando mediante diferencias finitas las derivadas que aparecen en (1) y mediante molificación discreta aproximamos la integral que allí también aparece, de manera similar a como se hizo en [5].
El artículo está organizado de la siguiente forma. En la sección 2 presentamos la discretización de nuestro modelo. En la sección 3 presentamos el análisis de convergencia de nuestro método para el cual establecemos algunos supuestos iniciales, y enseguida establecemos la condición CFL bajo la cual se garantiza la monotonía del esquema planteado, además que nuestro esquema cumple la ley conservativa, la propiedad de variación total decreciente (TVD) y regularidad. Finalmente, en la sección 4 desarrollamos algunos experimentos numéricos que muestran la eficiencia del método numérico que proponemos.
2. Aproximación Numérica
Para el tamaño de la malla se tomarán  , de modo que
, de modo que 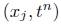 son los puntos en los que se evaluarán las aproximaciones del esquema numérico a la solución de (1), donde
son los puntos en los que se evaluarán las aproximaciones del esquema numérico a la solución de (1), donde  , para j entero y n un número natural mayor o igual que 1. La discretización del dato inicial está dada por:
, para j entero y n un número natural mayor o igual que 1. La discretización del dato inicial está dada por:
Evaluamos ahora la ecuación (1) en nuestra discretización, obteniendo:
Lo siguiente que haremos es aplicar el método de diferencias finitas para aproximar cada una de las derivadas que figuran en (1). Para los términos de (1) relacionados con la primera derivada utilizaremos diferencias finitas hacia adelante, mientras que para la segunda derivada espacial implementaremos diferencias finitas centradas. Denotando por 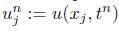 , llegamos a
, llegamos a
Y
Ahora procedemos a aproximar la integral que aparece en (3), mediante molificación discreta, de la siguiente forma.
Tomando ξ = s - xj ,se tiene
pues  para
para  y J es simétrica respecto al eje Y, de modo que
y J es simétrica respecto al eje Y, de modo que  para todo
para todo  .
.
De (7) y por la condición de Lipschitz sobre u y B(u), obtendremos la aproximación de la integral de la ecuación (3), donde  , para
, para 
Sea  . Entonces, si L denota la constante de Lipchitz para u tenemos lo siguiente
. Entonces, si L denota la constante de Lipchitz para u tenemos lo siguiente
Obsérvese ahora que si L1 denota la constante de Lipchitz para B(u) podemos deducir lo siguiente:
Ahora, definiendo
de modo que
llegamos a la aproximación de la integral,
pues cuando ξ esto en  se encuentra en Ii+
j
.
se encuentra en Ii+
j
.
El siguiente paso para llevar a cabo la aproximación numérica de la ecuación (1) es reemplazar (4), (5), (6), y (10) en (3), con lo cual obtenemos
Ahora definimos 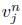 como nuestra aproximación de
como nuestra aproximación de  que satisface
que satisface
Estamos interesados en conocer la solución en el paso de tiempo n + 1, por lo que despejamos 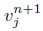 en (12):
en (12):
La ecuación anterior puede reescribirse en la forma siguiente
Ahora bien, utilizando el Teorema del Valor Medio y el teorema fundamental del cálculo tenemos
para 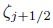 entre
entre 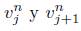 para
para  entre
entre 
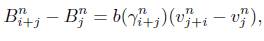 para
para  entre
entre 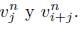
Teniendo presente lo anterior, (14) es equivalente a
que puede ser reescrita
donde los  se denominan pesos de la ecuación y se definen como
se denominan pesos de la ecuación y se definen como
(16) corresponde a la forma discretizada y linealizada de la ecuación (3).
3. Estabilidad y monotonía
En esta sección, se estudian los aspectos concernientes a la convergencia del esquema numérico propuesto, mostrando monotonía y algunas propiedades de regularidad de la solución aproximada. Partimos de unos supuestos iniciales que nos ayudarán en la prueba de algunos de los lemas propuestos en esta sección.
Hipótesis: Con la notación antes relacionada se asume, al igual que en [1], que existen constantes positivas M 1 y M 2 tales que
donde  corresponden a las funciones A(u) y B(u) evaluadas en el instante t = 0. Además asumimos
corresponden a las funciones A(u) y B(u) evaluadas en el instante t = 0. Además asumimos  .
.
Lema 3.1. (Monotonía) El esquema (16) es monótono bajo la condición CFL
Démonstration. Para cada  definidos en (17), se tiene que
definidos en (17), se tiene que  , si
, si  , esto es si
, esto es si
Lo anterior es equivalente a tener
para lo cual es suficiente que se satisfaga
ahora, factorizando y despejando Δt de (20), se obtiene la siguiente condición CFL del esquema
En el siguiente lema se muestra una propiedad que cumplen los pesos  , la cual es importante para análisis posteriores.
, la cual es importante para análisis posteriores.
Lema 3.2. Los pesos 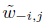 , definidos en (17) cumplen que
, definidos en (17) cumplen que
Demostración. Teniendo en cuenta la forma como están definidos los pesos 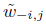 en (17), realizamos la suma de todos ellos a continuación:
en (17), realizamos la suma de todos ellos a continuación:
Lema 3.3. El esquema (13) es conservativo. Más precisamente, (13) se puede escribir en la forma
Donde
Demostración. Primero notemos que el último termino de (13) puede ser reescrito de la siguiente manera
Ahora, reemplazando (23) en (14) obtenemos
es decir
Se mostrarán, en los siguientes dos lemas, otros resultados concernientes a la estabilidad del esquema planteado.
Lema 3.4. Si la condición CFL (18) se satisface, entonces el esquema (13) es tal que
Demostración. Recuérdese que por (16) tenemos
de este modo, aplicando valor absoluto en ambos miembros de la anterior igualdad se obtiene
Lema 3.5. El esquema (13) cumple que
es decir,
Demostración. Aplicando valor absoluto en ambos miembros de la igualdad en (15) y sumando sobre todo  obtenemos
obtenemos
A continuacióon mostraremos que nuestro esquema cumple la propiedad de variación total decreciente (TVD). Recuerdese que para una funcion discreta z, se define la variación total de la siguiente forma:
Además, la propiedad TVD significa que  .
.
Lema 3.6. Nuestro esquema numérico (13) tiene la propiedad TVD, esto es:
Demostración. Recordemos que en (14) establecimos la siguiente equivalencia
Análogamente, se puede escribir  , obtenióendose el siguiente resultado
, obtenióendose el siguiente resultado
De acuerdo a lo anterior, si restamos miembro a miembro las ecuaciones (27) y (14) y luego reagrupamos tóerminos obtenemos
Aplicando ahora el Teorema del Valor Medio a la ecuación (28) tenemos
y el paso a seguir es aplicar valor absoluto y sumar sobre todo 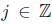 para obtener
para obtener
Se muestran ahora dos resultados claves de regularidad para el esquema numérico planteado.
Lema 3.7.
Si la condicion CFL (18) se satisface, entonces existe una constante C
1
independiente de y
y tal que
tal que
Demostración. Haciendo un procedimiento análogo al realizado inicialmente en el lema 3, podemos escribir  de la siguiente forma
de la siguiente forma
Ahora restamos miembro a miembro las ecuaciones (14) y (30) con el fin de obtener una expresión para 
Lo siguiente que haremos, es aplicar Teorema del Valor Medio en (31) para obtener
de donde
Ahora, si desarrollamos los productos y agrupamos términos nuevamente, se llega a
de donde se obtiene fácilmente la siguiente desigualdad
que equivale a tener
Haciendo inducción sobre n en (34) logramos obtener que
Por otro lado, si n = 0 en (12) tenemos
Igualdad de la cual se despeja 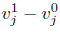 y se multiplica por
y se multiplica por 
De (36) el término más complicado de acotar es el último. Para realizar esto, recuerde que por (23)
pero note lo siguiente
Con
Así, reemplazando (37) en (23), el último termino de (36) se puede escribir como sigue
lo cual nos conduce a la igualdad siguiente:
Si hacemos n = 0 en (37) establecemos que
Si reemplazamos (38) en (36) obtenemos la siguiente expresión equivalente a la ecuación (36)
aplicando valor absoluto en esta última ecuación nos resulta la desigualdad
sumando ahora en (39) sobre todo 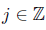 obtenemos
obtenemos
Ahora bien, utilizando los supuestos iniciales y los resultados obtenidos en (26), la ecuación (40) nos quedaría expresada de la siguiente manera
con lo cual concluimos
donde
Lema 3.8.
Si la condición CFL (18) se satisface, entonces existe una constante C
2, independiente de y
y , tal que
, tal que
Demostración. Por (37),  en (23) se puede expresar de la siguiente forma
en (23) se puede expresar de la siguiente forma
obsérvese además que
Transponiendo el último término al miembro izquierdo de la desigualdad obtenemos la siguiente expresión:
Ahora, primero sumando 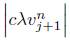 y luego multiplicando por
y luego multiplicando por  ambos miembros de (44) obtenemos la desigualdad
ambos miembros de (44) obtenemos la desigualdad
Por Lema 3, se tiene que 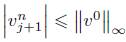 ; reemplazando esto en (45), tenemos
; reemplazando esto en (45), tenemos
Por último, multiplicando (46) por  se obtiene el resultado deseado
se obtiene el resultado deseado
Las propiedades probadas en los lemas de la sección 3 garantizan analíticamente la convergencia y estabilidad de nuestro esquema numérico, lo cual se pone en evidencia en la siguiente sección a través de diferentes experimentos numéricos.
4. Experimentos Numéricos
A continuación se presentan algunos experimentos numéricos, con los cuales se muestra la eficacia del método numérico propuesto en este artículo.
Ejemplo 1
En este primer ejemplo estudiamos una ecuación lineal no local propuesta en [5]. Se soluciona numericamente la ecuación (1), con 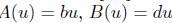 ,
,
condition inicial 
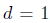 , un tiempo de
, un tiempo de 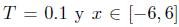 . La ecuación (1), con estos datos tiene como solución exacta
. La ecuación (1), con estos datos tiene como solución exacta
con
En la Figura 1 se hace la comparación entre la solución exacta de la ecuación del primer ejemplo y la solución aproximada encontrada a través del método que proponemos en este artículo.
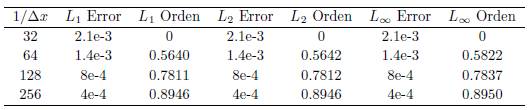
La Tabla 1 muestra errores y órdenes correspondientes a la ecuación tratada en el Ejemplo 4.1.
Se puede ver en la Tabla 1 que computacionalmente el orden de convergencia del método que proponemos es 1, lo cual coincide con lo descrito en la ecuación (11), además, la solución numérica que aquí proponemos converge a la solución exacta como se puede ver en la Figura 1.
A continuación, se muestran dos ejemplos con ecuaciones no lineales y no locales de las cuales no se tiene la solución exacta. Lo que haremos será programar una solución numérica con muchos puntos y la tomaremos como referencia para comparar nuestras soluciones programadas con pocos puntos en el dominio.
Ejemplo 2
Se soluciona numericamente la ecuación (1), con los siguientes datos
En la Figura 2, se muestra la soluciáon numáerica de la ecuaciáon tratada en este ejemplo, para distintos valores de 
En ambas figuras, la línea solida es la solución de referencia calculada con un valor de  = 1 /512.
= 1 /512.
La Tabla 2 muestra errores y órdenes correspondiente a la ecuación tratada en el Ejemplo 2.
Según los resultados de la Tabla 2, se puede observar que computacionalmente el orden de convergencia del método en este caso es de 1, aunque se haya tomado A(u) y B(u) con discontinuidades. Obsérvese que dichas funciones también cumplen con las propiedades exigidas al igual que la función J. Además, se puede notar en las Figuras 2 y 3 que nuestras soluciones para distintos valores de  convergen a la solución que programada como referencia.
convergen a la solución que programada como referencia.
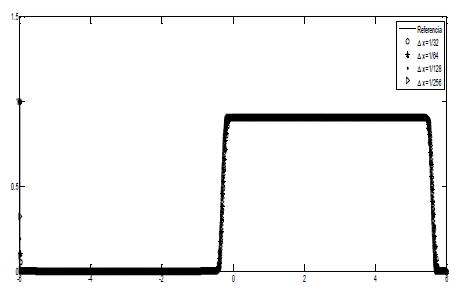
Ejemplo 3
Se soluciona la ecuación (1), con los siguientes datos
y condición inicial
En la Figura 3, se muestra la solución numérica de la ecuación tratada en este ejemplo, para distintos valores de  .
.
En la Figura 4, se muestra el acercamiento de una porcioón de la Figura 3.
En ambas gráficas, la línea solida es la solución de referencia calculada con un valor de Δx = 1/1024.
La Tabla 3 muestra los errores y los órdenes correspondientes a la ecuación tratada en el Ejemplo 3.
Nuevamente, se observa que el orden de convergencia de nuestro método es 1, aún cuando la condición inicial es discontinua. La soluciones programadas para distintos valores de Δx convergen a la solución de referencia que programamos como se observa en las Figuras 3 y 4.
5. Conclusiones
Se desarrolló un procedimiento numérico para la aproximación de soluciones a una ecuación diferencial parcial tipo parabólica con convección-difusión no lineal y no local, usando los métodos de diferencias finitas y molificación discreta, efectuando además el análisis de estabilidad para obtener las condiciones CFL asociadas a la discretización. Se lograron demostrar importantes propiedades tales como TVD, ley conservativa y lemas de regularidad, las cuales son imprescindibles para garantizar la convergencia de las soluciones del esquema estudiado.
Se realizaron experimentos numéricos, en los cuales se evidencia que el método que se propuso es de orden 1, lo que coincide con lo que se muestra en la ecuación (11). Además, aunque para las ecuaciones trabajadas en los Ejemplos 2 y 3 no se tienen soluciones exactas, en caso de que dichas soluciones se puedan calcular analíticamente, se garantiza que nuestras soluciones programadas para distintos valores de Δx convergerán a la exacta.
Los resultados numéricos obtenidos muestran que la implementación del método de molificación discreta es ventajoso en este tipo de problemas por cuanto regulariza muy bien la integral impropia que en nuestra ecuación aparece.
Para trabajos futuros, se puede realizar la aproximación a la ecuación no lineal, no local y fuertemente degenerada descrita por el modelo:
utilizando las mismas estrategias numéricas en este artículo empleadas, o discretizando las derivadas en tiempo y espacio con una misma clase de diferencias finitas (todas con diferencias finitas hacia atrás o centradas). También se podría pensar en extender este mismo modelo a dos o tres variables.