INTRODUCCIÓN
El nido sísmico de Bucaramanga es una de las zonas de mayor sismicidad intermedia en el mundo. Su zona focal representa una cuña de profundidades de 120 – 220 km donde la mayor sismicidad ocurre entre los 120 – 180 km. En superficie, donde se proyecta la ubicación del nido se observa el cambio de dirección de la cordillera oriental a través de los Sistemas de Fallas principales de la región (Santa Marta – Bucaramanga, Suárez, Boyacá – Belén, Gachetá – Chicamocha, Carmen, San Vicente, Salinas) (Coral-Gómez, 1990) (FIGURA 1).

FIGURA 1 MAPA DE UBICACIÓN DEL MARCO TECTÓNICO DE COLOMBIA EN DONDE A. MUESTRA LA UBICACIÓN DEL TERRITORIO COLOMBIANO Y SUS PRINCIPALES CARACTERÍSTICAS TECTÓNICAS DEBIDAS A LA SUBDUCCIÓN DE LAS PLACAS DE NAZCA Y CARIBE BAJO LA SURAMERICANA (TOMADO DE ZARIFI Y HAVSKOV, 2003), LAS FLECHAS BLANCAS MUESTRAN LA DIRECCIÓN EN LA QUE LAS PLACAS DE NAZCA Y CARIBE SE SUBDUCEN BAJO LA PLACA B. ZOOM DEL EVIDENTE CAMBIO DE ORIENTACIÓN QUE SUFRE LA CORDILLERA ORIENTAL JUSTO DÓNDE COMIENZA LA FRANJA SÍSMICA DEL DEPARTAMENTO DE SANTANDER; Y C. ZOOM DE ALGUNOS DE LOS SISTEMAS DE FALLA MÁS IMPORTANTES DE LA REGIÓN COMO LA FALLA SANTA MARTA – BUCARAMANGA Y LA FALLA SUÁREZ (MAPA GEOLÓGICO DE COLOMBIA, 2015).
Este trabajo se enfoca en la técnica conocida como tomografía sísmica, la cual tiene como objetivo principal la reconstrucción de la distribución del campo de velocidades en el interior de la tierra a partir de las observaciones de los tiempos de viaje de las ondas entre la fuente sísmica (hipocentro) y los receptores localizados en diferentes posiciones geográficas (Stein y Wysession, 2003).
NIDO SÍSMICO DE BUCARAMANGA
Un nido sísmico es una región en donde se puede observar una concentración inusual de actividad sísmica de manera más o menos continua: los hipocentros se encuentran concentrados a profundidades entre los 50 y 250 km, y con mayor intensidad que en las zonas adyacentes (Zarifi y Havskov, 2003). Los nidos profundos e intermedios están relacionados con las zonas de subducción; entre los cuáles se encuentran los nidos de Bucaramanga en Colombia, Vrencea en Rumania, e Hindo Kush en Afganistán (Tryggvason y Lawson, 1970).
Zarifi y Havskov (2003) muestran una compilación de mecanismos focales en los nidos de Hindu Kush (Afganistán) y Vrancea (Rumania) donde las soluciones son de fallas inversas, mientras que en el nido de Bucaramanga el mecanismo focal es variable, siendo en la mayoría de casos, mecanismos inversos. Casi todos los estudios coinciden en que la sismicidad en Vrancea es el resultado del progreso del desprendimiento de la placa de su parte superior (ruptura de la placa). En el nido de Bucaramanga e Hindu Kush, la fuerza motriz responsable no se conoce exactamente. Muchos estudios sugieren que, en el nido de Bucaramanga, el mecanismo responsable es la migración de fluidos o reacciones de deshidratación o un complejo campo de esfuerzo concentrado, mientras que en el nido de Hindu Kush el mecanismo posible es la colisión de dos placas subductivas de direcciones opuestas.
El nido sísmico de Bucaramanga está situado en la parte nororiental del territorio colombiano, aproximadamente entre las coordenadas 6,5° - 7° N y 73° - 73,5° W (FIGURA 1), que corresponde a la zona con una concentración singular de actividad sísmica a profundidades mayores a los 120 kilómetros (Perico-Martínez y Perico-Granados, 2014). En el área se registra aproximadamente un sismo con magnitud 4,7 por mes cerca de la ciudad de Bucaramanga (Prieto et al., 2012).
La actividad sísmica del nido de Bucaramanga se concentra en un volumen mucho más pequeño (128 km3 (Schneider et al., 1987)) que los otros nidos a profundidades intermedias de la misma clase (nidos de Vrencea e Hindo Kush) (Schneider et al., 1987; Zarifi y Havskov, 2003) (FIGURA 2); lo cual está asociado a la complejidad tectónica del territorio Colombiano (Zarifi y Havskov, 2003).

FIGURA 2 MODELO ESQUEMÁTICO DE LA INTERACCIÓN DE LAS PLACAS NAZCA Y CARIBE QUE SUBDUCEN BAJO LA PLACA SURAMERICANA; A) REPRESENTA LA LOCALIZACIÓN DEL NIDO SÍSMICO SUGERIDA POR VAN DER HILST Y MANN (1994); B) MUESTRA LA UBICACIÓN SUGERIDA POR PENNINGTON (1983) Y C) REPRESENTA EL MODELO MÁS ACTUAL SUGERIDO POR ZARIFI ET AL. (2007) (MODIFICADO DE ZARIFI ET AL., 2007).
Una de las teorías que explica el origen del nido sísmico, es la generación y migración de fluido acompañado de la fusión parcial de la peridiotita (roca ígnea característica del manto), causada por el escape de agua contenido en una dorsal oceánica o un arco de isla durante la subducción (Pennington, 1981) que a su vez es generada por el calentamiento y el cizallamiento a lo largo de los bloques de subducción (Schneider et al., 1987); o también puede deberse a un complejo campo de tensión dentro de la zona donde se ubica el nido sísmico (Zarifi y Havskov, 2003).
Debido a la complejidad del nido se han propuesto diversos modelos tectónicos por lo que es difícil establecer a qué placa subduciente se encuentra relacionado. Pennington (1983) sugiere que la placa del Caribe está subduciendo bajo la placa Suramericana en dirección Sur – Este, y por ende, estaría localizado en ésta placa. Van der Hilst y Mann (1994) proponen que el nido se encuentra localizado sobre la placa de Nazca, en el segmento redefinido como el Bloque de Bucaramanga; y un tercer modelo, sugiere que la colisión que ocurre entre ambas placas (Nazca y Caribe) es la causante de su sismicidad (Zarifi et al., 2007).
El registro de la sismicidad en la zona empezó a datarse desde siglo XVI con la identificación de 111 eventos con epicentro en el territorio santadereano hasta 1963 (Ramírez, 1969; Salcedo, 1999); 220 eventos de magnitud promedio por debajo de 4,5 entre 1963 y 1968 (Tryggvason y Lawson, 1970); 20 sismos con magnitud promedio debajo de 4,2 asociados al nido sísmico en 1976 (Pennington et al., 1981).
Entre 1978 y 1980, con la instalación de una estación sismológica permanente en Bucaramanga se registraron 742 sismos asociados al nido a profundidades entre los 110 y 160 km (Gómez-Padilla, 1980). Posteriormente en 1983, con la implementación de 12 estaciones sismológicas se registraron 140 eventos ocurridos en un volumen de 128 km3 en la zona (Schneider et al., 1987). Finalmente en 1985, las 16 estaciones sismológicas activas registraron un total de 92 sismos ocurridos en el nido de Bucaramanga (Rivera, 1989).
En promedio la magnitud de los eventos ocurridos es menor de 4,7; los cuales tiene origen en un volumen relativamente pequeño (128 km3 aproximadamente) y a grandes profundidades (140-180 kilómetros) (Salcedo, 1999).
METODOLOGÍA
Uno de los problemas fundamentales en la sismología corresponde a la localización de hipocentros, es decir, la ubicación espacio – temporal (Xs , Ys , Zs , ts ), siendo Xs , Ys , Zs , las coordenadas espaciales de la fuente (entendida esta como fuente puntual) y ts el tiempo de ocurrencia.
Por otra parte, también está el problema de determinar la estructura interna de la tierra, generalmente estudiada a partir de la determinación del campo de velocidades, principalmente a partir de los primeros arribos de la Onda P (Aki et al., 1976). Los dos problemas mencionados pueden ser abordados de manera conjunta (Crosson, 1976) o de manera separada (Aki et al., 1976). Lo fundamental que plantean varios autores, es la posibilidad y necesidad de desacoplar los dos problemas inversos (Kissling, 1988).
El problema simultáneo puede plantearse de la siguiente manera: En un conjunto de estaciones en superficie E 1, ..., Ep , (p – estaciones) se registran una serie de eventos S 1, S 2, ..., Sq , (q eventos sísmicos). Para cada evento sísmico, se requiere su localización espacio – temporal (X 1i , X 2i , X 3i , X 4i ) para i=1,2…,q; siendo X → X 1, Y → X 2, Z → X 3 y t → X 4; por otra parte, si la región en estudio, se divide en bloques V1 , V2 , ... Vl , donde cada bloque Vk se identifica por el valor de velocidad de propagación de la Onda P: VK , se requiere también el valor de la velocidad en cada uno de ellos; generados a partir de los tiempos de tránsito desde los hipocentros i hasta las estaciones j: T ij , i=1, 2, …, q; j=1, 2, …, p.
En general, los tiempos de tránsito se caracterizan por ser una función no lineal tanto de las coordenadas hipocentrales como de los parámetros del campo de velocidad (Kissling, 1988; Crosson, 1976):
T ij = T ij (X 1i , X 2i , ..., X 1q , X 2q , X 3q , X 4q , V 1, V 2, ... Vl ,)
La expresión analítica para los tiempos de tránsito es:
donde Hi son las coordenadas del i-ésimo hipocentro, Ej las coordenadas de la j-ésima estaciones y V = V(X 1, X 2, X 3) donde (X 1, X 2, X 3) es un punto típico de la curva (rayo) que une fuente – receptor (FIGURA 3).
Si se define la “lentitud” como U(X, Y, Z) = 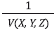 , la ecuación 1 se puede escribir como:
, la ecuación 1 se puede escribir como:
siendo ds el diferencial de longitud de arco.
Los tiempos de transito dependen de forma lineal del conjunto de parámetros U(X, Y, Z) y de forma no lineal de los puntos de los hipocentros Hi; por lo tanto la expresión 2 significa una dependencia no lineal del tiempo de tránsito T ij = (X 1i , X 2i , ..., X 1q , X 2q , X 3q , X 4q , V 1, V 2, ... Vl ,).
Dado el carácter no lineal, el problema de hallar las coordenadas espacio – temporal de los hipocentros (X 1i , X 2i , X 3i , X 4i ), i=1,…, q y los parámetros V 1, V 2, ... Vl , tiene que ser resuelto de manera iterativa, partiendo de una estimación inicial de las incógnitas ... Xki 0, donde K=1, 2, 3, 4; i=1, 2,…, q y Vl 0, donde l=1, 2, …, l, representando cada punto de la trayectoria.
Sea el tiempo estimado  , el cálculo posterior de Tij
podría ser resuelto por medio de una aproximación de primer orden de la Serie de Taylor (Aki y Richards, 1980):
, el cálculo posterior de Tij
podría ser resuelto por medio de una aproximación de primer orden de la Serie de Taylor (Aki y Richards, 1980):
o
La ecuación 4 puede escribirse de manera matricial:
con Δm = (ΔX 11, ..., ΔX 41, ΔX 12, ..., ΔX 42, ..., ΔX 4q , ΔV 1, ..., ΔVl ).
La matriz G es la que se muestra a continuación en forma de bloque:
donde:
k = 1, 2, …, q y:
Las submatrices S 1, S 2, ..., Sq hacen referencia a la parte hipocentral del problema y las submatrices M 1, M 2, ..., Mq se refieren a la parte tomográfica del problema simultáneo. El problema general a resolver está dado por la ecuación 5. En general, este problema es sobredeterminado. La primera opción para obtener una solución, es la utilización de los mínimos cuadrados, es decir, minimizar (GΔm – Δt)2 o lo que es equivalente, minimizar (GΔm – Δt) t . (GΔm – Δt) lo que lleva a las ecuaciones normales:
cuya solución sería:
Algunos autores, como Aster et al. (2013) y Crosson (1976) llaman a la matriz (GTG)-1 GT una inversa generalizada. Una característica importante desde el punto de vista computacional, y cuando hay un gran número de eventos sísmicos, es que la matriz GTG es una matriz dispersa, lo que implica ventajas en cuanto al almacenamiento de datos y también en cuanto a los cálculos a realizar. Sin embargo, para la solución de mínimos cuadrados existe el inconveniente de que la matriz GTG puede ser singular o también mal condicionada (Strang, 2009). Estos inconvenientes pueden ser entendidos a partir de la llamada descomposición en valores singulares de la matriz G.
G = U⋀VT
donde la matriz ⋀ tiene la forma:
por lo tanto:
Los valores ⋀1, ⋀2, ..., ⋀p son los valores propios de la matriz GTG. Cuando alguno de los valores de ⋀ i es muy pequeño, la matriz G será mal condicionada (Strang, 2009), lo que significa que la solución:
tendrá problemas de estabilidad, esto significa que para pequeños errores en los Δt, se podría obtener errores muy grandes en la soluciones Δm.
Como alternativa al problema mencionado anteriormente, está el llamado Algoritmo de Levenberg y Marquardt, el cual modifica la solución de mínimos cuadrados en la siguiente forma:
Minimizar {(GΔm – Δt) T . (GΔm – Δt) + β 2 Δm T . Δm}.
Minimizar ésta expresión es equivalente a resolver el siguiente sistema de ecuaciones normales (Aki y Richards, 1980; Aster et al., 2013):
Donde β es un coeficiente que se ajusta a los requerimientos del problema, este parámetro es llamado por algunos autores como parámetro de regularización de Tikhonov (Aster et al., 2013). La solución de la ecuación 12 es:
Este proceso, garantiza la estabilidad del sistema de ecuaciones a resolver; y es también llamado Método de regularización de Tikhonov.
El control de calidad de los resultados de la inversión, puede hacerse a través de la llamada Matriz de Resolución, que para el caso del algoritmo Levenberg – Marquardt viene dada por la siguiente expresión (Aki y Richards, 1980; Crosson, 1976): R = HG
donde H es la matriz:
H = (GTG + β 2 I)–1 GT
de manera que,
esta ecuación indica que, si la matriz R se diferencia de una matriz identidad I, entonces habrá una discrepancia entre lo calculado y lo real; por el contrario, si la matriz R tiende a la matriz identidad I (caso ideal), esto significaría que la inversión es exacta.
Para este trabajo, se utilizaron los softwares Velest (Kissling et al., 1994) y Simulps14 (Thurber, 1981; Thurber, 1992), los cuáles contienen los algoritmos que resuelven estas ecuaciones, de manera directa y transparente para el usuario de estos softwares. El modelo de velocidades para la Onda P en el interior del nido sísmico de Bucaramanga se obtuvo mediante el uso de la tomografía de velocidades calculada a partir de los tiempos del primer arribo a las estaciones (FIGURA 4, TABLA 1) de la Red Sismológica Nacional de Colombia (RSNC) de sismos ocurridos desde Enero de 2012 a Junio de 2016, inicialmente localizados entre 6° - 8°N y 72° - 74°W (zona nororiental del territorio colombiano) a profundidades entre los 0 y 200 kilómetros; posteriormente fueron solamente utilizados los sismos ocurridos entre 6,5° - 7°N y 73° - 73,5°W (zona en la que se encuentra localizado el nido de Bucaramanga).

FIGURA 4 MAPA DE LAS ESTACIONES SISMOLÓGICAS CERCANAS A LA ZONA DE ESTUDIO, ESTABLECIDAS POR LA RSNC.
TABLA 1 CARACTERÍSTICAS DE LAS ESTACIONES SISMOLÓGICAS ACTIVAS CERCANAS A LA ZONA DE ESTUDIO, DE LAS CUÁLES SE TOMARON LOS REGISTROS DE LOS PRIMEROS TIEMPOS DE LA ONDA P DE LOS SISMOS OCURRIDOS Y TOMADOS EN CUENTA EN ÉSTE TRABAJO.

Para generar el modelo de velocidades 1D se utilizó como modelo inicial el planteado por Londoño et al. (2010) (TABLA 2), en un estudio realizado cerca de la zona estudiada en éste trabajo, utilizando los tiempos de llegada de las Ondas P generadas por los sismos ocurridos, en éste estudio, se plantea la profundidad de Moho a los 37 kilómetros aproximadamente (Londoño et al., 2010).
TABLA 2 VALORES APROXIMADOS DEL MODELO DE VELOCIDAD DE LA ONDA P, PROPUESTO POR LONDOÑO ET AL. (2010).

El modelo de velocidades en 3D se generó a partir del modelo 1D obtenido (ver TABLA 6), sin embargo, se realizó un ajuste de éste, dado por la ecuación 15, para obtener las velocidades entre los 50 y 200 km de profundidad, debido a que en el modelo 1D se obtuvo un valor constante para la velocidad en el rango de la profundidad mencionada. Este ajuste se hizo mediante la técnica de mínimos cuadrados utilizando los datos de la TABLA 6.
RESULTADOS
Modelo de velocidades 1D
Para la inversión 1D, se utilizó el programa Velest (Kissling et al., 1994) ejecutado bajo Seisan (Havskov y Ottemoller, 1999), el cuál calcula los tiempos de llegada mediante el trazado de rayos para el campo de velocidades propuesto; una vez conocidos estos tiempos se determina el RMS (raíz media cuadrada de la diferencia entre los tiempos calculados y los tiempos observados). Inicialmente, se utilizó la subrutina Select del software Velest, para filtrar los eventos ocurridos según una serie de parámetros establecidos previamente (TABLA 3) y se seleccionaron 1138 sismos que cumplieron con ellos, los cuáles se utilizaron para generar el nuevo modelo de velocidades para la Onda P en una sola dimensión.
TABLA 3 PARÁMETROS CON LOS CUÁLES SE ESCOGIERON LOS 1138 SISMOS QUE SE UTILIZARON PARA LA INVERSIÓN 1D.

*Se estableció un máximo de 999 estaciones como referencia, para que se tomaran todas las estaciones que registraran cada uno de los eventos.
Se tomaron en cuenta diez parámetros de amortiguamiento (β) (ver sección anterior) para el proceso de inversión (TABLA 4), y se generaron sesenta modelos de velocidad divididos en seis grupos, donde el modelo inicial a partir del segundo grupo, es el modelo de velocidad con menor RMS obtenido en el anterior (TABLA 5). Finalmente, se escogió el modelo con β=1,0 del primer grupo, debido a que fue el que presentó el menor RMS general (FIGURA 5); para éste modelo se asume una homogeneidad lateral de manera que solo se toma en cuenta la variación de la velocidad en profundidad (Crosson, 1976), y así el modelo obtenido consta de cuatro capas con variación de la velocidad en cada una de ellas (TABLA 6).
TABLA 5 RMS OBTENIDOS PARA CADA UNO DE LOS MODELOS DE VELOCIDAD OBTENIDOS EN CADA GRUPO. LOS NÚMEROS SEÑALADOS, SON LOS VALORES DE LOS RMS MÁS BAJOS PARA CADA GRUPO DE MODELOS OBTENIDOS EN CADA UNA DE LAS INVERSIONES.


FIGURA 5 GRÁFICA DEL RMS OBTENIDO PARA CADA PARÁMETRO DE AMORTIGUAMIENTO Y GRUPO DE MODELOS DURANTE LA INVERSIÓN.
TABLA 6 VALORES DEL MODELO DE VELOCIDADES 1D PARA LA ONDA P EN LA ZONA DEL NIDO SÍSMICO DE BUCARAMANGA, GENERADO EN ÉSTE TRABAJO.

En la FIGURA 6 se hace una comparación entre el modelo inicial 1D utilizado (Londoño et al., 2010) y el obtenido en este trabajo, en donde se pueden observar los cambios en las velocidades de cada una de las capas; en la capa más superficial hay una variación aproximada de 0,78 km/s con respecto al modelo inicial, en la capa comprendida entre los 10 y 50 km hay una variación aproximada de 0,14 km/s, entre los 50 y 200 km, la variación es aproximadamente de 0,29 km/s y a partir de los 200 km de profundidad, es de 0,28 km/s.

FIGURA 6 COMPARACIÓN DE LOS MODELOS DE VELOCIDAD; LAS LÍNEAS PUNTEADAS INDICAN EL MODELO INICIAL UTILIZADO, LA LÍNEA CONTINUA INDICA EL MODELO GENERADO EN ÉSTE TRABAJO.
El siguiente paso, es obtener el modelo tridimensional a partir del modelo 1D obtenido en esta sección.
Modelo cuasi 3D
La inversión 3D se realizó utilizando el programa Simulps14 (Thurber, 1981; Thurber, 1992), el cual genera un modelo de velocidades por cada uno de los sismos utilizados. El modelo final es el promedio ponderado de todos ellos; para esto, se le da un peso a cada uno, dependiendo de la cercanía del hipocentro con respecto a la zona de estudio (nido sísmico de Bucaramanga, para este trabajo), es decir, a los eventos ocurridos dentro del nido sísmico se les dio un mayor peso que a aquellos ocurridos en los límites, o en la corteza. Inicialmente, se definió una malla cuyo volumen es de 8694×103 km3, con divisiones X-Y(latitud-longitud) de 23×21 con un espaciamiento de 10 y12 km respectivamente; se establecieron, además, un total de 12 capas a diferentes profundidades (TABLA 7), de manera que se trabajó con un total de 6762 bloques. Durante las primeras inversiones, se descartaron 794 sismos debido a errores en la localización o a su cercanía a los bordes de la malla; utilizándose al final un total de 344 eventos de los 1138 iniciales, para la determinación del modelo 3D; en el trazado de rayos de los eventos utilizados se observa una gran densidad de datos en la zona de estudio (FIGURA 7).

FIGURA 7 TRAZADO DE RAYOS DE LOS 344 EVENTOS UTILIZADOS Y REGISTRADOS EN CADA UNA DE LAS ESTACIONES SISMOLÓGICAS. A. PROYECCIÓN EN PLANTA DONDE SE APRECIA LA DENSIDAD DE RAYOS EN LA ZONA DEL NIDO SÍSMICO; B. VISTA CON RESPECTO A LA LATITUD, DONDE LA DENSIDAD DE LOS RAYOS SE ACUMULA ENTRE LOS 6,5° Y 7°N; Y C. VISTA CON RESPECTO A LA LONGITUD DONDE LOS RAYOS TIENEN UNA MAYOR DENSIDAD ENTRE LOS 73° Y 73,5°W.
TABLA 7 DIFERENTES PROFUNDIDADES Y VALORES DE LA VELOCIDAD, UTILIZADAS EN EL MALLADO Y EN LA GENERACIÓN DEL MODELO DE VELOCIDADES EN 3D.

En la TABLA 7 también se establecen los valores de la velocidad (en km/s) para cada una de las profundidades, obtenidas mediante el ajuste al modelo de velocidades 1D obtenido utilizando la ecuación 15.
Al igual que con el modelo 1D, se utilizaron diferentes parámetros de amortiguamiento (TABLA 8), y se determinó el punto donde la varianza de los datos y la varianza del modelo fuera compensable (Vargas et al., 2003); se eligió el parámetro de amortiguamiento 350 (FIGURA 8). Teniendo en cuenta los valores del RMS en el modelo propuesto por Londoño et al. (2010) y los obtenidos en este trabajo, se hizo un mejoramiento casi del 15,17%.

FIGURA 8 CURVA DE VARIANZA DEL MODELO CON RESPECTO A LA VARIANZA DE LOS DATOS, CON LA QUE SE DETERMINÓ QUE EL PARÁMETRO DE AMORTIGUAMIENTO (λ) MÁS ÓPTIMO, FUE 350.
Los resultados de la inversión 3D se muestran en la FIGURA 9 en función de las variaciones con respecto a la velocidad media de cada una de las capas del modelo 1D, como de los valores del campo de velocidades en cada uno de los bloques del modelo en 3D (Aki y Lee, 1976). En este trabajo, se obtuvieron 14 secciones a diferentes profundidades definidas en la TABLA 7, en donde se tiene una vista en planta del campo de velocidad en cada una de ellas.

FIGURA 9 VALORES DEL CAMPO DE VELOCIDADES DE ONDA P (KM/S) EN CADA UNO DE LOS BLOQUES DEL MODELO 3D REPRESENTADO EN 12 SECCIONES A DIFERENTE PROFUNDIDAD, A. 0 KILÓMETROS, B. 10 KILÓMETROS, C. 20 KILÓMETROS, D. 30 KILÓMETROS, E. 40 KILÓMETROS, F. 50 KILÓMETROS, G. 60 KILÓMETROS, H. 70 KILÓMETROS, I. 80 KILÓMETROS, J. 100 KILÓMETROS, K. 120 KILÓMETROS, Y L. 150 KILÓMETROS; LAS VARIACIONES LATERALES DE LA VELOCIDAD CON RESPECTO A LA PROMEDIO EN CADA UNA DE LAS PROFUNDIDADES SE DENOMINAN “ANOMALÍAS POSITIVAS” SI SON MAYORES QUE ÉSTA O “ANOMALÍAS NEGATIVAS” SI SON MENORES.
Dado que el nido de Bucaramanga se encuentra a profundidad mayor de 80 km, en esta sección de resultados solo se muestra la matriz de resolución para profundidades entre 80 y 150 km. En la FIGURA 10 se representa espacialmente la distribución de los elementos diagonales de la matriz de resolución (EDR) para tener una idea de cuál es la incertidumbre en los valores obtenidos para el modelo de velocidades en la FIGURA 9. Vargas et al. (2003) sugieren que las zonas del modelo obtenido que tienen una mejor resolución, son aquellas representadas en tonos claros en la distribución espacial EDR; esto se debe a que tanto la dirección y densidad de los datos, como el peso de las fases de Onda P ofrecen buenas perspectivas de resolución.

FIGURA 10 ELEMENTOS DIAGONALES DE LA MATRIZ DE RESOLUCIÓN DE LOS PARÁMETROS PARA LA INVERSIÓN DEL MODELO DE VELOCIDAD DE LA ONDA P EN 3D, SE TIENEN PLANOS A DIFERENTES PROFUNDIDADES, A. 80 KILÓMETROS, B. 100 KILÓMETROS, C. 120 KILÓMETROS Y D. 150 KILÓMETROS.
Para validar el proceso de inversión y comprobar la confiabilidad del modelo final de velocidad de este trabajo, se realizó una prueba estadística que consistió en perturbar el modelo obtenido (dado que no se conoce el modelo real) y se realizó la inversión tomando como referencia de modelo inicial el modelo perturbado y se obtuvieron nuevos modelos, se observó que en todos los casos la convergencia es hacia el modelo de referencia. Cabe aclarar que se tuvo en cuenta la zona a partir de los 80 km de profundidad por ser la más cercana al nido de Bucaramanga. Los resultados se muestran en la FIGURA 11. Dado que este proceso se realizó mediante el programa Simulps14, solo fue posible realizar una perturbación no mayor al 5%.
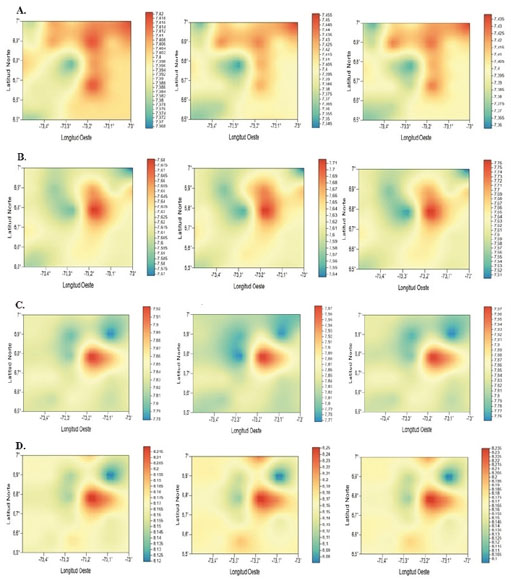
FIGURA 11 SE MUESTRA EL CONTRASTE ENTRE LAS VELOCIDADES OBTENIDAS A PROFUNDIDADES ENTRE LOS 80 Y 150 KM DEL MODELO FINAL DE ESTE TRABAJO, EL MODELO PERTURBADO Y EL GENERADO DURANTE EL SEGUNDO PROCESO DE INVERSIÓN. A. 80 KM DE PROFUNDIDAD Y LA VARIACIÓN ES DEL 0.2%, EN B. 100 KM Y LA VARIACIÓN ES DEL 1,04%, C. 120 KM DEL 0,63% Y D. 150 KM CON VARIACIÓN DEL 0,24% APROXIMADAMENTE.
La distribución espacial de EDR tiene lugar en las zonas en donde se tiene buena cobertura de rayos sísmicos (FIGURA 10), y se observan los cambios de velocidad que ocurren con respecto a la velocidad promedio del medio obtenida mediante la inversión 1D.
Las capas 80 y 150 kilómetros ofrecen valores de EDR medios (0,4 – 0,65) hacia las zonas en dónde las anomalías obtenidas en el modelo del campo de velocidad (FIGURA 10) empiezan a juntarse hacia el centro de la región estudiada, y valores un poco más bajos, a sus alrededores.
Los valores de EDR más altos se obtuvieron en las capas de 100 y 120 kilómetros (0,9 – 1); esto se debe a que la mayoría de los sismos utilizados tuvieron ocurrencias a profundidades entre los 100 y 150 kilómetros, de manera que se tuvo una mayor densidad de datos, la cual se evidencia en la FIGURA 7 del trazado de rayos.
Para validar el proceso de inversión y comprobar la confiabilidad del modelo final de velocidad de este trabajo, se realizó una prueba estadística que consistió en perturbar el modelo obtenido (dado que no se conoce el modelo real) y se realizó la inversión tomando como referencia de modelo inicial, el modelo perturbado, y se obtuvieron nuevos modelos; se observó que en todos los casos la convergencia es hacia el modelo de referencia. Cabe aclarar que se tuvo en cuenta la zona a partir de los 80 km de profundidad por ser la más cercana al nido de Bucaramanga. Los resultados se muestran en la FIGURA 11. Dado que este proceso se realizó mediante el programa Simulps14, solo fue posible realizar una perturbación no mayor al 5%.
DISCUSIÓN DE RESULTADOS
Modelo 1D
Las variaciones en los valores de la velocidad entre el modelo obtenido en este trabajo y el propuesto por Londoño et al. (2010) se deben en gran medida, a que los modelos no pertenecen a la misma zona, sino a regiones cercanas.
Teniendo en cuenta que el modelo de velocidad inicial utilizado en este trabajo presenta cuatro capas a profundidad, se obtuvieron también cuatro capas en el modelo de velocidades 1D en el cual la velocidad va aumentando conforme aumenta la profundidad. Las velocidades obtenidas en las dos primeras capas del modelo (0 a 10 km, y 10 a 50 km), corresponden a velocidades de la granodiorita, roca granítica composicional general de la corteza y al rango de velocidades que se puede encontrar en la corteza terrestre; las velocidades obtenidas a partir de los 50 km están relacionadas con las de la peridiotita, que es la roca ígnea característica del manto terrestre.
Con el modelo 1D generado en este trabajo se obtuvo un RMS (Raíz media cuadrada) de los tiempos residuales de 0,089232 s, que representa una reducción casi del 28% con respecto al RMS del modelo inicial obtenido por Londoño et al. (2010) que fue de 0,32.
Modelo 3D
Teniendo en cuenta el modelo de velocidades 1D generado y el ajuste que se le realizó para la inversión 3D, en éste trabajo se encontró que la Onda P en la corteza posee velocidades desde los 6,52 km/s hasta poco más de 6,85 km/s. Entre los 40 y 50 km de profundidad se presenta una variación composicional evidenciada en el aumento de la velocidad, además de un contraste en el tamaño de los cuerpos anómalos encontrados en el área de trabajo; debido a esto se sugiere que la discontinuidad de Moho se encuentra en esta zona. No es posible determinar la profundidad específica entre el rango de 40-50 km debido a que la resolución para éste trabajo es mayor de los 10 km.
De manera general, el modelo de velocidades en 3D determinó dos cuerpos anómalos en el área de estudio: a) una anomalía positiva (mayor velocidad que el promedio) y b) una anomalía negativa (velocidad inferior) que se hacen más evidentes entre los 60 y 150 kilómetros de profundidad. El primer cuerpo anómalo es interpretado como una ascensión y cristalización magmática, mientras el segundo está relacionado con la fusión parcial del magma por el cambio de composición. Las anomalías presentes en la zona del nido obtenidas en este trabajo, se pueden entender como dos cuerpos en dónde su composición comienza a variar poco antes de los 50 kilómetros de profundidad, cambiando la velocidad de propagación de Onda P en ellos. En el manto la velocidad promedio aumenta paulatinamente hasta alcanzar los 8,17 km/s a una profundidad de 150 kilómetros.
El magma empieza a ascender desde profundidades mayores a los 150 kilómetros, donde se presenta un acuñamiento total de los cuerpos magmáticos anómalos encontrados en el área del estudio, que se asocia a la cuña del manto siendo la zona que se localiza sobre una o más placas que se subducen bajo la corteza terrestre (Van Keken, 2003), es decir que dicho acuñamiento está posiblemente localizado sobre el punto donde convergen las Placas de Nazca y Caribe bajo la Placa Suramericana, siendo esta convergencia la responsable de la fusión parcial ocurrida a esa profundidad que facilita el ascenso del magma.
El acuñamiento que se empieza a presentar a partir de los 60 kilómetros de profundidad y que a su vez, se hace más evidente a partir de los 100 kilómetros, puede estar influenciado por la subducción de las Placas tectónicas, delimitando los cuerpos magmáticos.
La presencia de cuerpos magmáticos de menor velocidad al valor promedio en el manto, se deben a procesos de fusión parcial donde se originan magmas basálticos y quedan como residuos harzburgitas (80% olivino, 20% ortopiroxenos) y dunitas (100% olivino); mientras que los cuerpos con mayor velocidad que el valor promedio se deben a procesos de cristalización del magma a medida que este asciende.
El proceso de fusión parcial se hace evidente a los 100 kilómetros de profundidad en donde se presentan un cuerpo magmático en el que la Onda P se propaga a una velocidad aproximada de 7,59 km/s (menor a la velocidad promedio) que puede asociarse a un cuerpo de dunita (Anderson et al., 1968) como residuo de la fusión parcial, que se encuentra rodeado de un cuerpo con mayor velocidad asociado a la harzburgita. Por otra parte, a la misma profundidad se encuentra un cuerpo magmático en donde la velocidad de propagación de la Onda P es aproximadamente 7,64 km/s (mayor que la velocidad promedio) el cual se puede asociar a la presencia de piroxeno en altas proporciones en piroxenita y/o a la cristalización del magma y mineralización del piroxeno (Birch, 1960).
En la corteza se tienen tres capas con diferente velocidad promedio cada una, la primera va desde la superficie hasta los 10 kilómetros con una velocidad de 6,08 km/s; de los 10 a los 30 kilómetros se presenta una velocidad de 6,66 km/s y finalmente de los 30 a poco antes de los 40 kilómetros con una velocidad de 6,8476 km/s. En superficie, se tiene un medio aparentemente homogéneo dónde la velocidad promedio determinada es de 6,08 km/s; sin embargo, se encuentra una pequeña anomalía negativa (menor velocidad) en la zona de estudio que puede ser el resultado de un cambio en el gradiente local de temperatura, debido a que parte del fluido de la fusión parcial ocurrida a profundidad asciende hasta llegar a superficie. En superficie la anomalía negativa empieza a homogeneizarse con el medio general, esto se evidencia en que la diferencia entre las velocidades es mínima.
CONCLUSIONES
El modelo de velocidades 1D que se generó en éste trabajo tuvo una reducción casi del 28% en el RMS con respecto al modelo inicial utilizado lo cual indica que se obtuvo una mayor aproximación al modelo verdadero.
Se determinaron dos anomalías en el área de estudio: una anomalía negativa que es consecuencia de la fusión parcial ocurrida en la corteza y el manto terrestre asociada a un alto contenido de olivino; la segunda anomalía es generada por la cristalización del magma y está asociada al alto contenido de piroxenos.
La alta resolución del modelo obtenido está a partir de los 100 y 120 km de profundidad debido a la gran densidad de rayos y datos en ésta zona.
La sismicidad en el nido, también puede estar relacionada al acuñamiento que se empieza a presentar aproximadamente a los 120 km de profundidad, por influencia de la subducción ocurrida, y la fusión parcial ocurrida por los fluidos acuosos provenientes de parte de la placa subducida que recibe la cuña del manto a los 150 km de profundidad; en dónde el adelgazamiento de los cuerpos magmáticos anómalos se hace más evidente.



































