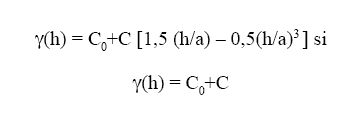Distribución espacial de las ninfas de Jacobiasca lybica (Hemiptera: Cicadellidae)
en un viñedo en Andalucía, España

 

Spatial distribution of the nymphs of Jacobiasca lybica (Hemiptera: Cicadellidae)
in a vineyard in Andalucia, Spain

 

JOSÉ FRANCISCO RAMÍREZ-DÁVILA¹ y ELVIA PORCAYO-CAMARGO²

¹ Profesor Investigador de la Facultad de Ciencias Agrícolas, UAEM. Centro Universitario El Cerrillo Piedras Blancas Km. 15 Carr. Toluca - Ixtlahuaca Entronque al Cerrillo. C.P. 50200 Toluca, Méx. Tel. (01 729) 296 55 31 Ext: 139. jframirezd@uaemex.mx.

² Pasante de la Facultad de Geografía UAEM. Cerro de Coatepec s/n Ciudad Universitaria, C.P. 50000, Toluca, México. elvia_pcamargo@yahoo.com.

---

Resumen: Se determinó la distribución espacial de las ninfas del mosquito verde Jacobiasca lybica a lo largo de un año en una parcela de regadío, en Cádiz, España. Los resultados demostraron que las poblaciones de ninfas dentro de la zona de estudio presentaron una distribución agregada, formándose varios centros de agregación, hecho corroborado por los mapas elaborados mediante el Krigeado. La infestación no fue uniforme y se logró detectar una estabilidad espaciotemporal de las poblaciones de ninfas. Se logró determinar además que, es posible mediante las técnicas de Agricultura de Precisión reducir los costos económicos y ambientales.

Palabras clave: Mosquito verde. Geoestadística. Estabilidad espacial y temporal. Costo económico. Costo ambiental.

---

Abstract: The spatial distribution of nymphs of the green mosquito Jacobiasca lybica was determined over one year in an irrigated plot in Cadiz, Spain. The results showed that populations of nymphs within the study area had an aggregated distribution, forming several centers of aggregation, a fact corroborated by maps produced through Kriging. The infestation was not uniform and it was possible to detect a spatial-temporal stability in nymphal populations. It was also determined that it is possible through the techniques of precision agriculture to reduce economic and environmental costs.

Key words: Green mosquito. Geostatistics. Spatial and temporal stability. Economic cost. Environmental cost.

---

Introducción

En Jerez (España) se ha elaborado vino desde hace siglos con variedades de uvas blancas, y la que se conoce hoy como Palomino fino, es la que los lugareños denominaron Listán común, siendo la cepa predominante en la región (García de Luján et al. 1990). Esta variedad de uva es fundamental para la elaboración de los vinos de la zona y se adapta de forma excelente a la poda jerezana y a los suelos de albariza, siendo en estos pagos donde se obtienen los mostos de mayor calidad además, la variedad es básica para la elaboración de los vinos de Jerez (Fernández de Bobadilla 1956).

Se conoce como “mosquito verde” a un grupo de insectos chupadores, cicadélidos, que afectan a la viña y a un gran número de plantas silvestres y cultivadas. Las especies encontradas son varias (Freitas y Amaro 2001; Mazzoni et al. 2001). En España las dos especies de mosquito verde más comunes sobre el viñedo son Jacobiasca lybica (Bergenin y Zanon, 1922) y Empoasca vitis (Göthe, 1875) (Hemiptera, Cicadellidae). Estas especies se diferencian entre sí en la forma en que se encuentran las estructuras del tubo anal y los ápices de los apéndices del pigóforo (Ocete et al. 1999). En Jerez el insecto más abundante es J. lybica llegando a desfoliar totalmente las cepas, impidiendo la normal maduración del racimo y agostamiento de los sarmientos (Toledo 1992).

Toledo (1992) indica que si el ataque del mosquito verde se produce en las primeras fases de desarrollo de los brotes, afectan a las hojas terminales, donde aparecen decoloraciones y desecaciones marginales más o menos pronunciadas. Estas desecaciones están limitadas con las zonas verdes con ribetes de color amarillo en las variedades de vid blancas y rojo en las variedades de vid tintas. También se observan crispaciones del borde de la hoja con un arrollamiento sobre el envés. Sobre brotes aparecen entrenudos cortos y brotes anticipados.

Si el ataque tiene lugar en una fase más avanzada –finales de julio-agosto-septiembre– entonces los síntomas se localizan sobre las hojas ya formadas. Sobre variedades tintas se observan manchas angulosas de color rojo a partir del borde hacia el interior de la hoja, delimitadas por los nervios, formando un mosaico. Sobre variedades blancas se observan decoloraciones y amarillamientos, acompañados o no de una desecación marginal de color rojizo (Toledo 1992).

El adecuado control de insectos plaga es uno de los aspectos más importantes en el manejo de cualquier cultivo, tanto desde el punto de vista económico como ecológico (Mazza et al. 1996; Hall et al. 1997; Castella et al. 1999). Un correcto control va estrechamente ligado al conocimiento de la distribución espacial del insecto. Los métodos comúnmente utilizados en la estadística “clásica” para el estudio de las distribuciones espaciales de los insectos se basan en el uso de las distribuciones estadísticas e índices de dispersión, y por consiguiente no tienen en cuenta la exacta localización espacial de la muestra. Ello produce ciertos efectos indeseables como fallar al diferenciar patrones espaciales diferentes, y sus descripciones de los patrones espaciales son altamente dependientes del tamaño de las unidades de muestreo y de la relación entre la media y la varianza (Sawyer 1989; Hurlbert 1990) y no tienen en consideración toda la información espacial el interés en el uso de distintas ramas de la estadística espacial. Una de las ramas frecuentemente disponible. A causa de estos problemas y la disponibilidad de paquete estadísticos apropiados, se ha incrementado el uso de la Geoestadística que tiene la ventaja de caracterizar la distribución espacial en un espectro de escalas y direcciones múltiples, además de ser independientes de la relación entre la media y la varianza.

Los métodos geoestadísticos proporcionan una medida más directa de la dependencia espacial, debido a que tienen en cuenta la naturaleza bidimensional de la distribución de los organismos a través de su exacta localización espacial, además, permiten elaborar mapas de gran utilidad (Isaaks y Srivastava 1988; Oliver y Webster 1991; Rossi et al. 1992; Speight, et al. 1998; Sciarretta et al. 2001; Blom y Fleischer 2001). Por otra parte, una de las metas de la Agricultura de Precisión es dirigir las medidas de control sobre las zonas específicas de infestación de un insecto plaga. Con el uso de la Geoestadística es posible establecer mapas de la distribución espacial de insectos y el porcentaje de infestación de los mismos sobre un área de estudio, con lo cual es posible conseguir ahorros económicos y ambientales al poder dirigir las aplicaciones de insecticidas hacia las zonas específicas de infestación de un insecto plaga. El objetivo central de este trabajo entonces fue establecer y modelar mediante el método geoestadístico la distribución espacial de las ninfas del mosquito verde Jacobiasca lybica en un viñedo de regadío en Jerez, España.

Materiales y Métodos

Para el estudio se estableció una parcela experimental (de regadío), en el Centro de Investigación y Formación Agraria “Rancho de la Merced”, localizado en el Marco de Jerez, Cádiz (España), situada entre 36º31’15” - 36º54’60”N y 5º27’15”- 6º23’90”W, durante el año 2006. Los muestreos se realizaron durante la fase de mayor actividad del insecto que corresponde al periodo comprendido entre los meses de Junio y Octubre.

La parcela constaba de 1925 cepas de la variedad Palomino fino, separadas entre sí por aproximadamente 1 m, con una extensión de 3,700m² cada una. En la parcela se estableció una malla rectangular (Oliver y Webster 1990) de 35 x 55 cepas.La hilera de 35 cepas fue considerada como líneas para muestrear, a partir de esto, el muestreo se realizó cada dos líneas, partiendo de la primera línea, es decir, en total se muestrearon 18 líneas y 17 quedaron sin muestrear. De cada línea muestreada se tomaron siete cepas para cada muestreo, con un intervalo de nueve cepas entre sí, por lo tanto, en cada parcela se muestrearon 126 cepas. Los muestreos fueron realizados durante cinco fechas que abarcaron la etapa más importante del ciclo biológico de la especie, tal y como lo menciona Toledo (1992). Cabe señalar, que los muestreos se realizaron mensualmente y que fueron muestreadas en cada fecha las mismas cepas.

En cada muestreo se contó el número de ninfas del mosquito verde hallados en 10 hojas por cepa tomadas al azar abarcando la parte superior, media e inferior de cada cepa y se estableció un promedio de ninfas por cepa, según la metodología establecida por López (1997). Las cepas muestreadas en las cinco fechas se señalaron con antelación en la base con pintura fluorescente color blanco y con una etiqueta que identificaba su posición indicando la línea y columna correspondiente. Las cepas muestreadas en la parcela fueron georreferenciadas con un DGPS para tener una ubicación espacial precisa de las mismas.

Se realizó una exploración estadística de los datos originales de las poblaciones de ninfas del mosquito verde. Se realizó una transformación logarítmica de los datos [log10(n+1)] para normalizarlos. En cada fecha de estudio se calculó un semivariograma experimental a partir de los valores registrados de número de ninfas de mosquito por planta se calculó con la siguiente expresión (Journel y Huijbregts 1978; Isaaks y Srivastava 1989):(for1)

donde: Υ*(h) es el valor experimental del semivariograma para el intervalo de distancia h; N(h) es el número de pares de puntos muestrales separados por el intervalo de distancia h; z(x_i) es el valor de la variable de interés en el punto muestral xi y z(x_i+h) es valor de la variable de interés en el punto muestra x.+h. Cualquier función matemática puede usarse para modelar un semivariograma siempre que reúna las condiciones de ser positiva y definida (Armstrong y Jabin 1981). En la práctica, se escoge como modelo una de las funciones para las que se sabe que dichas condiciones se cumplen (Isaaks y Srivastava 1989). Un procedimiento habitual es la selección visual de una función que parezca ajustarse a los valores experimentales del semivariograma y realizar posteriormente una validación (Englund y Sparkas 1988). En este trabajo, eligió un modelo esférico que se define la siguiente expresión (Isaaks y Srivastava 1989):(for2)

donde: C₀ es el efecto pepita; C₀+C es la meseta y a representa el alcance.

La validación de los diferentes modelos esféricos ajustados a los semivariogramas experimentales de cada una de las cinco fechas estudiados se realizó con el procedimiento denominado validación cruzada (Isaaks y Srivastava 1989). Con este procedimiento, se elimina un valor muestral y se emplea el método de interpolación geoestadístico denominado krigeado, junto con el modelo de semivariograma a validar, para estimar el valor de la variable de interés en dicho punto muestral a partir de los restantes valores muestrales. Este proceso se efectúa sucesivamente en todos los puntos muestrales y las diferencias entre los valores experimentales y los estimados se resumen mediante los denominados estadísticos de validación cruzada (Isaaks y Srivastava 1989; Hevesi et al. 1992). Los parámetros del modelo a validar (C_0' C ya) se van modificando en un procedimiento de prueba y error hasta la obtención de estadísticos de validación cruzada adecuados. Estos estadísticos son los siguientes:

a) Media de los errores de estimación (MEE)

donde: z*(x_i) es el valor estimado de la variable de interés en el punto xi.; z(x_i) es el valor medio de la variable de interés en el punto x_i y n es el número de puntos muestrales realizados en la interpolación. El MEE no debe ser significativamente distinto de 0 (test t), en cuyo caso, indicaría que el modelo de semivariograma permite el cálculo de estimativos no sesgados.(for3)

b) Error cuadrático medio (ECM)(for4)

Un modelo de semivariograma se considera adecuado si, como regla práctica ECM es menor que la varianza de los errores muestrales (Hevesi et al. 1992).

c) Error cuadrático medio adimensional (ECMA) (1992).(for5)

donde: δ_k es la desviación estándar del error esperado en la estimación con el Krigeado.

La validez del modelo se satisface si ECMA está comprendido entre los valores 1±2 (2/N)^0.5.

Resulta de gran importancia determinar que tan fuerte es la relación entre los datos obtenidos en los muestreos lo anterior es posible conocerlo al calcular el nivel de dependencia espacial. Este valor se obtiene al dividir el efecto pepita entre la meseta y el resultado es expresado en porcentaje. El nivel de dependencia espacial se considera alto si el resultado es menor de 25%, se considera que el nivel de dependencia espacial es moderado si se encuentra entre 26 y 75% y se considera que el nivel de dependencia es bajo si es mayor del 76% (Cambardella et al. 1994).

Una vez que se validaron los modelos de los correspondientes semivariogramas se utilizó el Krigeado, éste es el método de interpolación geoestadístico que permite que la estimación no tenga sesgo de valores asociados a puntos que no fueron muestreados. En este estudio se empleó el método del Krigeado Ordinario para obtener las estimaciones respectivas. Las estimaciones de las poblaciones de ninfas del mosquito verde en la parcela experimental se realizaron utilizando el programa WinGslib 2002. Cuando se obtuvieron las estimaciones correspondientes con el método del Krigeado para cada muestreo, se realizaron los mapas que indicaron el comportamiento espacial de las poblaciones de ninfas del mosquito verde en el Marco de Jerez. Las estimaciones se representaron en forma de mapa mediante la utilización del programa Surfer 9.0.

Resultaba interesante determinar si existía una estabilidad espacio-temporal a corto plazo (dentro de un año), de las poblaciones de ninfas de J. lybica. Para tal efecto se compararon las estimaciones obtenidas con el método del Krigeado. Las comparaciones se realizaron utilizando una modificación de la prueba estadística no paramétrica de Cramér- von Mises realizada por Syrjala (1996) tal y como lo aconsejan Liebholdet al (1993). Cabe indicar que las comparaciones fueron realizadas con resultados de fechas próximas entre sí tal y como lo indican Rossi et al. (1992).

Agricultura de Precisión (AP): estimación de la superficie infestada y evaluación económica y ambiental.

Se estableció la superficie infestada de los mapas elaborados, utilizando el programa Surfer 9.0. Una vez obtenido el porcentaje de superficie infestada en cada uno de los mapas se calculó el costo de una aplicación normal de insecticida, tal como la realizan los agricultores en la zona, y el costo de una aplicación dirigida (sólo áreas infestadas). La diferencia entre ambos valores nos indicó el ahorro económico obtenido con la metodología de precisión. Igualmente, procedimos a realizar el cálculo correspondiente al ahorro en la cantidad de producto utilizado bajo ambas estrategias de control. De esta manera se tendría una idea de la disminución del impacto nocivo hacia el ambiente, ya que al reducir la cantidad de insecticida en el manejo de las poblaciones de ninfas del mosquito verde, se reduce asimismo, el impacto ambiental.

Resultados

De acuerdo con los resultados de la validación cruzada (Tabla 1), se halló que en todos los casos el modelo que produjo el mejor ajuste a los datos fue el modelo esférico con efecto pepita (nugget effect) que denoto una estructura espacial agregada de las ninfas (Tabla 2). En la Tabla 2 se distingue que en el caso del efecto pepita sus valores se hallaron entre 0,05 encontrado en el segundo y tercer muestreo y 0,03 hallado en el cuarto y quinto muestreo. El valor del efecto pepita fue menor del 63% del valor de la meseta en todos los semivariogramas realizados. De esto se deduce que al menos el 37% de la variación total se debió a la dependencia espacial en la escala de muestreo.

En cuanto a la meseta los valores se encontraron entre 0,12 del cuarto muestreo y 0,06 del quinto muestreo. Los valores del alcance fluctuaron entre 53,20 m del cuarto muestreo y 29,18 m del primer muestreo (Tabla 2). El nivel de dependencia espacial entre los datos en todos los casos fue moderada. En la Fig. 1 se aprecian los modelos de Semivariogramas ajustados, establecidos para cada uno de los datos de la parcela experimental.

Mapas de densidad. La distribución de las poblaciones de ninfas del mosquito verde se encuentra agrupada en la Fig. 2. Se aprecia una gran cantidad de centros de agregación en todos los mapas, asimismo, las densidades medias de ninfas en cada muestreo fueron elevadas, lo anterior puede suponer una relación entre ambos aspectos. Los focos de agregación se distribuyeron por toda la parcela de estudio. Los focos de agregación más importantes debido a su mayor densidad se localizaron principalmente en el área central-izquierda de los mapas respectivos. También en este caso la invasión de la parcela parece provenir del costado izquierdo, es decir, de cepas vecinas localizadas en ese flanco.

Superficie infestada. El área sin infestar se encontró entre 84% y 52,8% del área total muestreada, con un valor medio de 31,52%. Se logró detectar que al aumentar la densidad de las ninfas disminuyó el porcentaje de superficie sin infestar, con una pequeña excepción en el muestreo del 27 de septiembre, donde a pesar de registrarse la mayor densidad de ninfas, el área libre de infestación aumentó ligeramente con respecto a la del muestreo anterior. En el último muestreo esta superficie libre de infestación aumentó de forma significativa al reducirse notoriamente la densidad de ninfas. Todo esto indica que el mosquito verde de forma natural no invade el 100% del área que infesta, es decir, la infestación no es uniforme sobre el área afectada.

Estabilidad espacial y temporal a corto plazo. En la Tabla 3 se pueden ver los resultados de la comparación de los mapas de ninfas de J. lybica entre las diferentes fechas de muestreo, utilizando la prueba estadística bivariable de Cramér-von Mises, modificada por Syrjala (1996). Se observa diferencia significativa entre las comparaciones de los muestreos del 27 de junio y el 25 de julio (γ = 1,88 y P = 0,02) y los muestreos del 27 de septiembre y 28 de octubre (γ = 1,71 y P = 0,01). En las restantes comparaciones entre fechas no se detectó diferencia alguna. Las densidades más altas se presentaron en los tres muestreos centrales, situación que permitió detectar una distribución semejante de las ninfas en dichos muestreos.

Evaluación económica y ambiental. En la Tabla 4 se observan los resultados de la superficie infestada y no infestada por parte del mosquito verde. Como se observa en la mencionada tabla, la infestación del insecto plaga nunca cubrió el 100% del área de estudio.

El malatión en polvo al 4% es el insecticida utilizado de forma primordial para el control de las poblaciones del mosquito verde en una dosis de 12 kilos por hectárea, considerando que el kilo tiene un valor de 0,51 céntimos de Euro, una aplicación sobre una hectárea entera tendría un costo de 6,12 Euros. En términos reales el ahorro económico no es muy importante. Este intervalo para las ninfas se encontraría entre 3,05 y 0,97 Euros/ha, con un ahorro promedio de 1,91 Euros/ ha (Tabla 5). El ahorro ambiental, sin embargo, resulta muy interesante, ya que se evitaría utilizar una cantidad importante de insecticida al dirigir las medidas sobre zonas específicas. En las ninfas dicho ahorro se hallaría entre 6,05 y 1,95 kilos/ ha con 3,80 kilos/ha de ahorro medio. Como se aprecia el ahorro económico es mayor cuando las poblaciones del insecto son más bajas y por lo tanto se han dispersado menos por la parcela experimental.

Discusión

Dentro del área de la estadística espacial es cada vez más común el uso de la Geoestadística como una herramienta de modelación de multitud de fenómenos biológicos (Rossi et al. 1992). Uno de los campos más beneficiados es la protección de cultivos donde el conocimiento de la distribución espacial es de vital importancia para el manejo de plagas, enfermedades y malas hierbas (Liebhold et al. 1993).

En este estudio, el nivel de dependencia espacial indica una distribución agregada de las poblaciones de ninfas. El hecho de que las densidades medias de las ninfas fueran altas en todos los muestreos permitió encontrar un tipo de agregación similar en todos los casos. La validación de los semivariogramas correspondientes corrobora la distribución en agregados de las poblaciones de ninfas de este insecto plaga. Cabe señalar, que Brenner et al. (1998) encontraron que los valores del efecto pepita en los semivariogramas que elaboraron para las ninfas de Blattella asahinai, comprendían entre el 30 y el 63% del valor de la meseta. Dichos valores son similares a los encontrados en los semivariogramas de las ninfas de J. lybica.

Además, la validación de los semivariogramas, nos permite tener certeza de que el método de muestreo y la escala de muestreo utilizado en el estudio eran apropiados. En el análisis geoestadístico demuestra ser una herramienta apropiada para el estudio de la distribución espacial de insectos plaga. Los resultados de este trabajo son parecidos a los reportados por Schotzko y O’Keeffe (1989) Liebhold et al. (1991) Sciarretta et al. (2001) y Blom y Fleischer (2001). Se registró que las densidades medias de ninfas entre las fechas en las cuales no había diferencia significativa eran parecidas y relativamente altas, lo que ocasionó que la distribución de las ninfas fuera similar en estos casos. Solamente a densidades altas se detecta una estructura espacial estable en el tiempo. Dicha estabilidad es de gran importancia para conocer con anticipación probables zonas con infestaciones importantes del insecto.

Por otra parte, en los mapas se apreció claramente que al aumentar la densidad, aumentó de forma general la superficie infestada, lo que resulta lógico al incrementarse la dispersión de las ninfas. Al disminuir la densidad de ninfas en el último muestreo hay un descenso importante de la superficie infestada. La mayor infestación del insecto plaga se localizó en el área central izquierda en la mayoría de los mapas esto se debió a que las cepas en mejor estado fisiológico se encontraban en esta parte de la parcela, por lo cual, las ninfas se vieron más atraídas hacia dicha zona. Fleischer et al. (1999) indican que de forma general la relación existente entre la densidad media de los insectos y la cantidad de centros de agregación se puede apreciar en los mapas de densidad elaborados mediante la técnica del krigeado. Entre los trabajos realizados con estadíos preimaginales de insectos en los cuales la relación mencionada haya sido registrada se pueden citar los realizados por Schotzko y O’Keeffe (1989) en un estudio con Lygus hesperus (Knight 1917); Liebhold et al. (1991) con la polilla gitana; Gribko et al. (1995) con la polilla gitana; Weisz et al. (1996) con el escarabajo colorado de la papa y Speight et al. (1998) con la cochinilla castaña.

Como demuestran los resultados, el mosquito verde no invade el 100% del área que infesta, es decir, la infestación no es uniforme. Un comportamiento similar en otros insectos plaga ha sido reportado por Gribko et al. (1995) Magro et al. (1999) y Schotzko y Quisenberry (1999). Lo hallado en este estudio abre las puertas a una aplicación dirigida de las medidas de control sobre las áreas que realmente están infestadas con el insecto plaga, lo cual hace factible obtener ahorros económicos y ambientales. Con respecto a lo anterior, considerando en conjunto los resultados de la evaluación económica y ambiental creemos que la reducción de la aplicación de importantes cantidades de insecticidas justifica el uso de las técnicas de la Agricultura de Precisión para controlar las poblaciones de ninfas del mosquito verde en viñedo.

El aumento constante de las densidades conforme pasaron los muestreos parece ser clave en la determinación de la estabilidad espacial y temporal a corto plazo de las poblaciones de ninfas de J. libyca según lo apreciado en los mapas elaborados. Al existir una densidad baja en el primer muestreo y al disminuir la densidad en el último muestreo y realizar la comparación respectiva de los mapas, se hace presente una diferencia significativa. Lo anterior señala que las ninfas del insecto presentan estabilidad a densidades altas. Tal estabilidad es de gran relevancia para poder dirigir medidas de control hacia puntos concretos de infestaciones altas.

Conclusiones

En términos de que fue posible establecer el tipo de distribución espacial y los mapas de densidad de las ninfas del mosquito verde, podemos concluir que la aplicación de la Agricultura de Precisión en el manejo de las poblaciones de este insecto plaga es factible; ya que al poder modelar la estructura espacial del insecto y determinar su exacta distribución en los mapas elaborados, es posible dirigir las medidas de control hacia zonas específicas de infestación, lo cual beneficiaría al productor al reducir sus gastos de producción y el impacto nocivo sobre el ambiente. Lo anterior resulta de mayor interés al extrapolar la posibilidad de la aplicación de la Agricultura de Precisión en toda la zona vitícola del Marco de Jerez, España, ya que la reducción en la aplicación de insecticidas innecesarios redundaría en un ahorro económico de cantidades importantes considerando la extensión en hectáreas cultivadas con vid. Asimismo, el ambiente de todo el Marco de Jerez vería reducidos los impactos residuales que los insecticidas provocan.

Literatura citada

ARMSTRONG, M.; JABIN, R. 1981. Variogram models must be positive-definite. Mathematical Geology 13(5): 455-459.        [ Links ]

BLOM, E.; FLEISCHER, S. 2001. Dynamics in the spatial structure of Leptinotarsa decemlineata (Coleoptera: Chrysomelidae). Environmental Entomology 30 (2): 350-364.        [ Links ]

BRENNER, R.; FOCKS, D.; ARBOGAST, R.; WEAVER, D.; SHUMAN, D. 1998. Practical use of spatial analysis in precision targeting for integrated pest management. American Entomologist 79-101.        [ Links ]

CAMBARDELLA, C.; MOORMAN, T.; NOVAK, J.; PARKIN, T.; KARLEN, D.; TURCO, R.; KONOPKA, A. 1994. Field scale variability of soil properties in central Iowa soils. Soil Science Society of America Journal 58: 1501-1511.        [ Links ]

CASTELLA, J.; JOURDAIN, D.; TREBUIL, G.; NAPOMPETH, B. 1999. A systems approach to understanding obstacles to effective implementation of IPM in Thailand: Key issues for the cotton industry. Agriculture Ecosystems and Environment 72 (1): 17- 34.        [ Links ]

ENGLUND, E.; SPARKS, A. 1988. GEO-EAS (Geostatistical Environmental Assessment Software) User´s Guide. U.S. Environmental protection agency document EPA/600/4-88/033. Environmental Monitoring Systems Laboratory, Las Vegas, NV, USA.        [ Links ]

FERNÁNDEZ DE BOBADILLA, G. 1956. Viníferas jerezanas y de Andalucía Occidental. I.N.I.A. Madrid. 141 p.        [ Links ]

FLEISCHER, J; BLOM, E.; WEISZ, R. 1999. Sampling in precision IPM: When the objective is a map. The American Phytopathological Society 89 (11): 115-118.        [ Links ]

FREITAS, J.; AMARO, P. 2001. “Explosion” de Cicadelle verte dans la région du Doura au Portugal en juillet/aout 1998. Integrated Control in Viticulture IOBC wprs Bulletin 24 (7): 217-219.        [ Links ]

GARCÍA DE LUJAN, A; PUERTAS, B.; LARA, M. 1990. Variedades de la Vid en Andalucía. Junta de Andalucía. Consejería de Agricultura y Pesca. Sevilla. 253 p.        [ Links ]

GRIBKO, L.; LIEBHOLD, A.; HOHN, M. 1995. Model to predict gypsy moth (Lepidoptera: Lymantriidae) defoliation using kriging and logistic regression. Environmental Entomology 24(3): 529- 537.        [ Links ]

HALL, D.; CHILDERS, C.; EGER, E.; ALLEN, J. 1997. Citrus rust mite (Acari: Eriophidae) counts on fruit and the negative binomial distribution. Florida Entomologist 80 (1): 1-10.        [ Links ]

HEVESI, J.; ISTOK, J.; FLINT, A. 1992. Precipitation estimation in mountainous terrain using multivariate geostatistics. Part. I. Structural analysis. Journal of Applied Meteorology 31 (7): 661- 676.        [ Links ]

HULBERT, S. 1990. Spatial distribution of the montane unicorn. Oikos 58: 257-271.        [ Links ]

ISAAKS, E.; SRIVASTAVA, M. 1988. Spatial continuity measures for probabilistic and deterministic geostatistics. Mathematical Geology 20 (4): 313-341.        [ Links ]

ISAAKS, E.; SRIVASTAVA, M. 1989. An introduction to applied geostatistics. Oxford university press, Nueva York. 561 p.        [ Links ]

JOURNEL, A.; HUIJBREGTS, C. J. 1978. Mining geostatistics. Academic Press, London, United Kingdom. 600 p.        [ Links ]

LIEBHOLD, A.; XU ZHANG HOHN, M.; ELKINTON, J.; TICEHURST, M.; BENZON, G.; CAMPBELL, R. 1991. Geostatistical analysis of gypsy moth (Lepidoptera: Lymantriidae) egg mass populations. Environmental Entomology 20 (5): 1407- 1417.        [ Links ]

LIEBHOLD, M; ROSSI, E.; KEMP, P. 1993. Geostatistics and Geographic Information Systems in applied Insect Ecology. Annual Review of Entomology 38: 303-327.        [ Links ]

LÓPEZ, M. A. 1997. Incidencia de Kalotermes flavicollis (Fabr.) (Isoptera: Kalotermitidae) En el Marco de Jerez/ Ensayos de técnicas blandas de control sobre plagas del viñedo. Tesis Doctoral University of Sevilla. 477 p.        [ Links ]

MAGRO, A; ARAÚJO, J.; HEMPTINNE, L. 1999. Coccinellids (Coleoptera: Coccinellidae) in citrus groves in Portugal: listing and analysis of geographical distribution. Boletín de Sanidad Vegetal - Plagas 25: 335-345.        [ Links ]

MAZZA, S.; CONTRERAS, G.; VIDELA, M.; POLAK, J.; SCHROEDER TANNURE, C. 1996. Técnicas de muestreo para la evaluación de infestación por pulgones (Aphis gossypii) en algodón (Gossypium hirsutum). Reunión de Comunicaciones Científicas y Tecnológicas SGCYT-UNNE Actas 3 (5): 1-4.        [ Links ]

MAZZONI, V.; COSCI, A.; LUCCHI SANTINI, L. 2001. Ocurrence of leaf hoppers (Aucheno rrhyncha, Cicadellidae) in three vineyards of the pisa district. Integrated Control in Viticulture IOBC wprs Bulletin 24 (7): 267-271.        [ Links ]

OCETE, R.; LÓPEZ, A.; QUARTAU, J.; PÉREZ, A. 1999. La problemática actual de los Mosquitos Verdes (Homoptera, Cicadellidae) en diversas zonas vitícolas españolas. Viticultura/ Enología profesional 63: 16-20.        [ Links ]

OLIVER, M.; WEBSTER, R. 1990. Statisticals methods in soil and land resource survey. Oxford University Press, Oxford. 232p.         [ Links ]

OLIVER, M.; WEBSTER, R. 1991. How geostatistics can help you. Soil use and Management 7 (4): 206 -217.        [ Links ]

ROSSI, R.; MULLA, J.; JOURNEL, G.; FRANZ, H. 1992. Geostatistical tools for modeling and interpreting ecological spatial dependence. Ecological Monographs 62 (2): 277-314.        [ Links ]

SAWYER, J. 1989. Inconstancy of taylor´s b: simulated sampling with different quadrat sizes and spatial distributions. Reserches on Populaation Ecology 31: 11-24.        [ Links ]

SCHOTZKO, D.; O´KEEFFE, L. 1989. Geostatistical description of the spatial distribution of Lygus hesperus (Heteroptera: Miridae) in Lentils. Journal of Economic Entomology 82 (5): 1277-1288.        [ Links ]

SCHOTZKO, D.; QUISENBERRY, S. 1999. Pea leaf (Coleoptera: Curculionidae) Spatial Distribution in Peas. Environmental Entomology. 28(3): 476-484.        [ Links ]

SCIARRETTA, A.; TREMATERRA, P.; BAUMGÄRTNER. 2001. Geostatistical análisis of Cydia funebrana (Lepidoptera: Tortricidae) pheromone trap catches at two spatial scales. American Entomologist 47 (3): 174-184.        [ Links ]

SPEIGHT, M.; HAILS, R.; GILBERT, M.; FOGGO, A. 1998. Horse chestnut scale Pulvinaria regalis (Homoptera: Coccidae) and urban host tree environment. Ecology 79 (5): 1503-1513.        [ Links ]

SYRJALA, E. 1996. A statistical test for a difference between the spatial distributions of two population. Ecology 77 (1): 75-80.        [ Links ]

TOLEDO, J. 1992. Mosquitos verdes. Los parásitos de la vid. Estrategias de protección razonada. MAPA-Ediciones Mundi-Prensa. España. Pp. 67-70.        [ Links ]

WEISZ, R; FLEISCHER, J.; SMILOWITZ, Z. 1996. Site specific integrated pest management for high value crops: Impact on potato pest management. Journal of Economic Entomology 89: 501- 509.         [ Links ]

Recibido: 4-jul-2008 - Aceptado: 24-oct-2008