ARTICULOS

¹ Este trabajo se ha realizado con la financiación concedida al proyecto SEJ2004-05872/PSIC del Ministerio Español de Ciencia y Tecnología.
² Correspondencia: SONIA ROMERO. Correo electrónico: soniajaneth.romero@uam.es

ABSTRACT

This paper presents an illustration of the integration of cognitive psychology and psychometric models to determine sources of item difficulty in an Arithmetic Test (AT), constructed by the authors, by means of its analysis with the LLTM. In order to reach this aim, a group of operations required to solve the items of the test were proposed, the dimensionality was evaluated, and the goodness of fit of items to both the Rasch and the LLTM models was studied. Results obtained were used to illustrate the advantages and limitations of the LLTM for the componential measurement; the main techniques used in the analysis were also introduced.

Key words: LLTM model, Rasch model, dimensionality.

RESUMEN

En este trabajo se presenta un ejemplo sobre cómo integrar la psicología cognitiva con la psicometría para determinar las fuentes de dificultad de los ítems de un Test de Aritmética (TA), construido por los autores, por medio de su análisis con el modelo LLTM. Para alcanzar este propósito se han propuesto un grupo de operaciones necesarias para resolver los ítems del test,se ha evaluado su dimensionalidad y se ha estudiado el ajuste de los ítems tanto al modelo de Rasch como al LLTM. Los resultados obtenidos mediante el análisis del TA han permitido ilustrar las ventajas y limitaciones del LLTM en la medición componencial, así como presentar las principales técnicas empleadas en el proceso.

Palabras clave: modelo LLTM, modelo de Rasch, dimensionalidad.

INTRODUCCIÓN

En las últimas décadas se ha generado un amplio interés por el desarrollo de modelos psicométricos que tienen en cuenta los procesos, atributos, operaciones o estrategias utilizados por las personas al resolver los ítems de un test. Los fundamentos teóricos que guían el desarrollo de dichos modelos constituyen un nuevo enfoque en la teoría de los test que está basado en la integración entre psicología cognitiva y psicometría (Rupp & Mislevy, 2006), dicha integración ha permitido que las fortalezas de un área compensen las deficiencias de la otra y viceversa. Cortada de Kohan (2000) enfatiza la importancia de la relación entre la psicología cognitiva y la psicometría y resalta su utilidad para que los tests estén al servicio de la comprensión de los procesos de aprendizaje.

El acercamiento entre las teorías cognitivas y la psicometría ha producido importantes cam-bios en diversas áreas de la medición: en primer lugar ha repercutido en el diseño de las pruebas pues desde este enfoque se procura que la teoría cognitiva subyacente acerca del constructo que se pretende medir sea la que oriente la construcción del test, proceso que ha sido llamado por algunos autores “perspectiva centrada en el constructo” (Embretson, 1985; Messick, 1984).

En segundo lugar ha repercutido en los objetivos de la medición puesto que los modelos propuestos bajo una perspectiva cognitiva permiten interpretar no solo las respuestas del sujeto sino los pasos intermedios ejecutados para obtener dichas respuestas, haciendo que el énfasis ya no sea en el resultado sino en el proceso; esto tiene implicaciones para el análisis y las inferencias que se realzan sobre las puntuaciones de los examinados y finalmente ha repercutido en los procesos de validación puesto que se ha incrementado el interés en acopiar evidencia sobre la correspondencia entre la teoría cognitiva subyacente y los procesos realmente usados por los sujetos en la solución de las tareas o ítems.

Un buen ejemplo de este acercamiento entre teoría cognitiva y psicometría son los llamados “modelos componenciales” (Embretson, 1999; Fischer, 1995; Van der Linden & Hambleton, 1997), que se caracterizan por: 1) especificar las operaciones mentales que intervienen en la solución de cada ítem, y 2) proponer un modelo de Teoría de Respuesta al Ítem (TRI) que obtenga la probabilidad de acierto en el ítem a partir de sus propiedades estructurales y del nivel de habilidad del sujeto evaluado.

Los modelos componenciales se han aplicado a la resolución de muchos tipos de tareas: problemas espaciales con figuras tridimensionales (Bejar, 1990, 1991; Bejar & Yocom, 1986), matrices tipo Raven (Hornke & Habon, 1986), problemas de análisis lógico (Revuelta & Ponsoda, 1998), tareas de razonamiento abstracto (Embretson, 1999), problemas de álgebra (Dimitrov & Raykov, 2003; Medina-Díaz, 1993), operaciones aritméticas básicas (Real, Olea, Ponsoda, Revuelta & Abad, 1999) y operaciones con fracciones y números mixtos (López & Elosua, 2002).

El conocimiento sobre los componentes requeridos para la respuesta correcta de los ítems es importante para un mayor entendimiento de la naturaleza de las habilidades específicas requeridas para resolver el test y para el desarrollo de instrumentos válidos, este conocimiento puede ayudar a los profesores a desarrollar estrategias de enseñanza más eficientes, mejorar contenidos curriculares y ofrece una información diagnóstica mucho más completa pues permite conocer los componentes en los que los examinados tienen dominio y también detectar aquellos en los que presentan dificultades.

Modelo Logístico Lineal de Rasgo Latente (LLTM).

El Modelo LLTM (Fisher, 1973) fue el primer modelo componencial desarrollado y el que ha sido empleado con mayor frecuencia; este modelo descompone la dificultad de los ítems en una suma ponderada de componentes como se puede ver en la siguiente expresión:

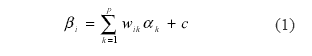
El LLTM permite estimar además de los niveles de rasgo de las personas y la dificultad de los ítems, la contribución de los diferentes componentes a dicha dificultad. El LLTM fue desarrollado para analizar tests en los que se conoce la “estructura” de cada ítem en términos de los componentes necesarios para su correcta resolución, que son determinados mediante una teoría subyacente o por medio de estudios empíricos previos a la aplicación del modelo; dicha estructura se refleja en la denominada matriz de pesos (W) de la siguiente manera: si para resolver correctamente el ítem i se requiere el componente k, el peso será wik=1; en caso contrario, será w=0.

Para usar correctamente el modelo LLTM se deben cumplir tres requisitos: 1) el ajuste previo del modelo TRI de Rasch a los datos, 2) poner a prueba si se cumple la ecuación (1), es decir, si el modelo LLTM reproduce adecuadamente los parámetros del modelo de Rasch y 3) conviene hacer estudios de validación del modelo cognitivo en el que se basa, representado formalmente en la matriz W.

El primer contraste requiere el análisis del cumplimiento de los supuestos del modelo de Rasch y la evaluación de su ajuste. Un supuesto básico del modelo de Rasch es la unidimensionalidad. Existen varios métodos para su evaluación (véase por ejemplo la revisión de Tate, 2003). Se puede emplear un Análisis Factorial (AF) a partir de la matriz de correlaciones tetracóricas. También se puede analizar la estructura factorial de los datos con modelos compensatorios multidimensionales como el de ojiva normal implementado en NOHARM (Fraser, 1988). Embretson y Reise (2000) resaltan la utilidad del NOHARM, tanto de manera exploratoria como confirmatoria, especialmente cuando los ítems requieren el uso de componentes. Finalmente, el índice de ajuste al modelo de Rasch proporciona implícitamente una evaluación de la unidimensionalidad de los datos.

El segundo contraste pone a prueba si el modelo LLTM reproduce adecuadamente los parámetros del modelo de Rasch, esto se sueñe hacer mediante el estadístico razón de verosimilitud condicional (en inglés, CLR), también llamado ÷2 de Andersen pues su distribución es ÷2 con gl=k-1-p grados de libertad, siendo gl la diferencia entre los parámetros independientes en los dos modelos. El test CLR se complementa con el análisis de la correlación entre las dificultades de los ítems estimadas en los dos modelos y con una representación gráfica de la misma: una mayor correlación implica un mejor ajuste. El test CLR presenta el problema de que frecuentemente produce un estadístico significativo (Fischer, 1995; López & Elosua, 2002; Medina-Díaz, 1993; Real et al, 1999), lo que conduce al rechazo del modelo LLTM aun cuando el ajuste gráfico y el coeficiente de correlación indiquen compatibilidad entre las dificultades estimadas con los dos modelos.

El tercer contraste requiere la realización de estudios de validación de los componentes expresados formalmente en W, pues los componentes propuestos, y sólo ellos, deben explicar las diferencias en los parámetros de los ítems. La validez de W depende por tanto de la calidad del modelo psicológico cognitivo disponible acerca de la tarea. A pesar de la importancia del estudio de la validez de los procesos subyacentes a la ejecución de los test, se han propuesto pocas técnicas para acopiar evidencia de la misma: en 1993, Medina-Díaz propone la Asignación Cuadrática (en inglés, QA); Dimitrov y Raykov (2003) proponen el uso de modelos de ecuaciones estructurales (en inglés, SEM) y Dimitrov (2007) propone el método de la distancia mínimocuadrática (en inglés LSDM).

El Test de Aritmética (TA) y su estructura componencial.

El TA contiene 32 ítems de selección múltiple con 4 opciones de respuesta, cada ítem contiene una adición o sustracción entre dígitos enteros. Un ejemplo de ítem es:

(-6) - (3) = a) 9 b) 3 c) -3 d) -9

Este test ha sido especialmente diseñado para niños que acaban de aprender el concepto de suma y resta con números enteros. Real, Olea, Ponsoda, Revuelta y Abad (1999) analizaron una versión anterior del TA llamada “Test de Signos” (Alonso & Olea, 1997) con un formato diferente en el cual se ofrecía solo una solución y el alumno debía decidir si ésta era correcta o incorrecta. En el estudio de Real y col (1999) se propusieron 8 procesos para la solución del test de signos, sin embargo el LLTM no ajustó bien. Como Baker (1993) ha encontrado, el LLTM es muy sensible a los errores de especificación en la matriz de pesos W, esto implica la necesidad de acopiar cuidadosa evidencia sobre la validez del modelo cognitivo que subyace a la aplicación del LLTM. En consecuencia, Romero, Ponsoda y Ximénez (2006), tras un estudio sistemático de la teoría sobre el proceso de enseñanza/aprendizaje de la aritmética básica con números enteros (Alarcón, 1994; Hughes, 1986; Kamii, 1989; Maza, 1999; Mialaret, 1984; Orton, 1996) proponen otra estructura cognitiva para los ítems de adición y sustracción del Test de Signos, basada en 6 operaciones. Los autores encontraron apoyo parcial de la estructura propuesta en un estudio de validación mediante el enfoque de ecuaciones estructurales (Dimitrov & Raikov, 2003), aunque un procedimiento complementario de triangulación mostró una mayor evidencia de apoyo para dicha estructura.

El objetivo del presente trabajo es analizar el Test de Aritmética mediante el modelo LLTM utilizando para ello la estructura cognitiva de 6 operaciones, cuya validez fue previamente estudiada en Romero, Ponsoda y Ximénez (2006). Para alcanzar dicha meta, se evaluó la dimensionalidad del test, se estudió el ajuste de los ítems al modelo de Rasch y finalmente se aplicó el modelo LLTM, evaluando su ajuste y analizando la contribución de las operaciones propuestas a la dificultad de los ítems.

MÉTODO

Procedimiento

El trabajo se desarrolla en tres fases que se corresponden con los objetivos específicos anteriormente mencionados:

1) Estudio de la dimensionalidad: se evaluó mediante el Modelo de Análisis Factorial de Fraser (1988). El análisis del ajuste del modelo se valoró por medio del índice de Tanaka (T). Aunque no hay unas normas de interpretación para este índice generalmente aceptadas (Gierl, Tan & Wang, 2005), se ha propuesto que valores por encima de 0,9 indican ajuste aceptable (Rouse, Finger y Butcher, 1999). Para realizar estos análisis se ha usado el programa NOHARM de Fraser (1988).

2) Calibración y ajuste modelo de Rasch: para la calibración se usó el programa LPCM-Win 1.0 (Fischer & Ponocny-Seliger, 1998). Para obtener el ajuste de los ítems se utilizó el programa RASCAL (Assessment Systems Corporation, 1996).

3) Aplicación del modelo LLTM: El procedimiento incluye la estimación de parámetros básicos y la evaluación del ajuste del modelo. Para ello se usó el programa LPCM-Win 1.0 (Fischer & Ponocny-Seliger, 1998).

Muestra y recolección de datos

La muestra consta de 432 niños españoles (55% hombres y 45% mujeres) de edades entre 12 y 14 años. El test fue administrado en el escenario del salón de clase a 316 estudiantes de tres colegios públicos de Madrid y 116 estudiantes de un colegio público de Albacete (España). La recolección de datos fue supervisada por los autores del presente estudio.

Instrumento

El test contiene 32 ítems de elección múltiple con operaciones de suma y resta entre dígitos enteros. Se presentan 4 opciones de respuesta para cada ítem (una de las cuales es incorrecta).

Se requirió expresamente a los estudiantes mostrar las operaciones que llevaban a cabo al resolver cada ítem en un espacio designado para ello con el objetivo de evitar el acierto por “adivinación”. El coeficiente de fiabilidad, Alfa de Cronbach, que evalúa la consistencia interna de las puntuaciones binarias fue de 0,91 para esta muestra, indicando muy buena fiabilidad del TA.

Operaciones Cognitivas.

Como se mencionó anteriormente se hipotetizaron 6 operaciones cognitivas que subyacen a las respuestas correctas en los 32 ítems del test, por tanto se produce una matriz W de 32 (ítems) x 6 (operaciones). Las operaciones propuestas son:

O1: Adición entre números naturales (a+b);

O2: Sustracción entre números naturales (ab) cuando a>b;

O3: Identificación del componente mayor en valor absoluto y planteamiento de resta del me-nor al mayor.

O4: Cambiar las posiciones de a y b;

O5: Determinar el signo (positivo o negativo) del resultado;

O6: Convertir la sustracción en adición y cambiar el signo al segundo componente.

A forma de ejemplo, el ítem número 3 en el test, (-6)+(5) debería requerir aplicar primero O3: 6-5, luego O2: 1 y finalmente O5: -1. La matriz W (Tabla 1) contiene la estructura cognitiva propuesta, nótese que el ítem 3 tiene un 1 en las casillas correspondientes a las operaciones que requiere y 0 en el resto de procesos. Para establecer dicha estructura se recurrió al estudio sistemático de la forma de resolver este tipo de tareas, se realizaron entrevistas a profesores de matemáticas y a algunos alumnos mientras resolvían la prueba y se revisaron materiales curriculares.

RESULTADOS

Estudio de la dimensionalidad

Como se puede ver en la última columna de la Tabla 1, el análisis de la dimensionalidad del TA utilizando Modelo de Análisis Factorial de Fraser confirma, como se esperaba, que los 32 ítems del test miden una sola dimensión (habilidad en aritmética básica), con un índice Tanaka bastante alto (0,9327) cumpliéndose así el supuesto de unidimensionalidad. Además las car-gas factoriales son todas positivas y grandes (el menor valor corresponde al ítem Nº 7: 0,272), indicando que todos los ítems contribuyen adecuadamente a la medida del rasgo latente.

Ajuste al modelo de Rasch y LLTM

La Tabla 2 muestra los parámetros de dificultad b estimados para cada ítem según el modelo de Rasch y su error típico, los resultados muestran que 7 de los 32 ítems no tienen buen ajuste al modelo de Rasch (p<0,01) por lo tanto dichos ítems fueron eliminados del análisis posterior con el LLTM; es importante recordar que el ajuste del modelo de Rasch es una condición previa para la correcta aplicación del LLTM. En la tabla 2 también se puede ver la re-calibración de los 25 ítems que presentaban buen ajuste al modelo de Rasch y los parámetros b recuperados por el LLTM correspondientes a cada ítem. Con respecto a la dificultad de los ítems se puede observar que, como cabía esperar, los ítems más fáciles (parámetros b negativos) han sido las sumas entre números positivos y los más difíciles (parámetros b positivos) han sido las restas entre números de distinto signo tipo (a)-(-b), (-a)-(b) y las restas entre números negativos (-a)-(-b).

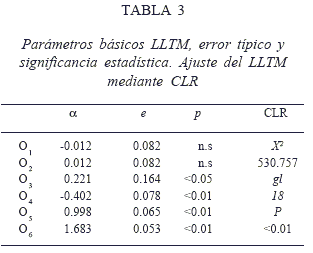
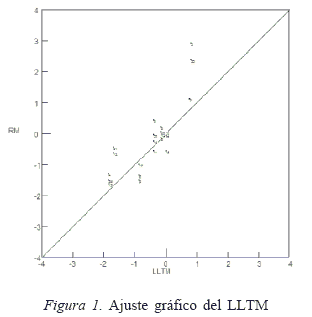
Finalmente, la tabla 3 contiene los parámetros básicos a estimados para cada operación, su significación estadística y los estadísticos de ajuste (CLR). La figura 1 presenta el ajuste gráfico del modelo LLTM.

La correlación de Pearson entre las dificultades estimadas por los dos modelos es alta (0,85) indicando buen ajuste del LLTM, esto se observa también en la gráfica correspondiente en la Figura 1. A pesar de lo anterior, el estadístico CLR ha resultado significativo, por lo tanto no se confirma el ajuste. Tal resultado no es sorprendente, pues es conocido (Fischer, 1995) que con frecuencia el CLR resulta significativo aunque el ajuste visual y la correlación sean adecuados.

En general, observando la Tabla 3 se puede ver que 4 de los 6 parámetros básicos son significativos, indicando que las operaciones correspondientes contribuyen a la dificultad de los ítems. Esto era de esperarse pues los dos primeros parámetros (que no han sido significativos) corresponden a la suma y resta de enteros positivos que son operaciones que los estudiantes a esa edad ya ejecutan de manera automática. Con respecto a las operaciones restantes 3 de ellas contribuyen a la dificultad de los ítems (parámetros básicos negativos) y 1 a la “facilidad” (parámetro básico positivo). La operación que contribuye en mayor medida a la dificultad de los ítems es el O6 : convertir la sustracción en adición, esto era de esperarse pues es un proceso doble que implica no solo cambiar el operador resta por suma sino también cambiar el signo del segundo componente, por ejemplo (-a)-(-b)=-a+b.

Otra operación que contribuye en buena medida a la dificultad de los ítems es O5: determinar el signo del resultado, esto también coincide con lo que se esperaba ya que el alumno debe conocer y aplicar varias reglas para realizar esta operación adecuadamente, por ejemplo debe saber que el resultado de sumar dos números negativos es también negativo (-a)+(-b)=-c. Una operación que contribuye a la dificultad, aunque en menor medida es el planteamiento de la resta entre el número mayor en valor absoluto y el menor (O3), esta operación solo se usa en ítems de suma entre números de distinto signo y se esperaba que tuviese una fuerte contribución a la dificultad, sin embargo su contribución ha resultado más bien moderada. Finalmente el intercambio entre los componentes a y b (O4) ha sido la única operación que hace los ítems más fáciles.

DISCUSIÓN

En este estudio se ha analizado la dificultad de los ítems del TA a partir de las operaciones mentales requeridas por este tipo de tareas de aritmética básica. Para ello se ha empleado una extensión del modelo de Rasch llamada LLTM, en el cual la dificultad del ítem se considera un indicador de la complejidad cognitiva requerida para resolver correctamente los ítems (Prieto y Delgado, 1999); esta complejidad se explica a su vez por los procesos, operaciones, estrategias y estructuras de conocimiento subyacentes a la ejecución del ítem, en concreto, los parámetros básicos estimados en el LLTM nos permiten conocer la contribución de las operaciones cognitivas propuestas a la dificultad de los ítems. Sin embargo, este modelo también presenta algunas limitaciones: al ser un modelo unidimensional no es apropiado cuando se tiene una prueba que mide mas de un rasgo latente, en el presente trabajo, el estudio de la dimensionalidad nos ha llevado a concluir que se cumple la condición de unidimensionalidad, pero esta es una característica que no es fácil de conseguir en muchos casos.

Otra limitación de este modelo es su carácter compensatorio pues la descomposición de los parámetros de dificultad es lineal (aditiva), en la práctica esto implica que la ejecución correcta de una operación “compensa” la ejecución incorrecta en otra. Es por esta razón que algunos parámetros básicos estimados han de ser positivos, en otras palabras, han de contribuir a la “facilidad” de los ítems. En el presente trabajo teóricamente todas las operaciones deberían contribuir a la dificultad de los ítems, sin embargo la estimación del parámetro básico O4 (intercambio de posición entre a y b) ha resultado positiva, indicando su contribución a la facilidad para resolver el ítem, esta interpretación debe ser tomada con precaución pues puede ser un artificio del modelo para “compensar” la negatividad de los demás parámetros.

A pesar de las anteriores limitaciones el modelo LLTM comparte con los otros modelos psicométricos de descomposición cognitiva algunas de las ventajas de este prometedor enfoque: la significación estadística de los parámetros básicos permite identificar cuáles son los componentes más importantes para la correcta resolución de los ítems y por el contrario cuáles tienen poca o nula influencia en la dificultad. Otro aporte del modelo es que mediante la magnitud de los parámetros básicos se puede conocer la fuerza de la contribución de las operaciones involucradas en la dificultad del ítem.

El LLTM también es útil para analizar ítems presentados en diferentes condiciones experimentales que puedan influenciar la dificultad y para analizar el cambio de los parámetros de dificultad en diseños de medidas repetidas (Fisher & Ponocny-Seliger, 1998). Aunque el presente trabajo no explora dichas posibilidades, es interesante que en futuros estudios se extiendan las aplicaciones de este modelo que permitirían, por ejemplo, analizar los efectos del aprendizaje de las tareas aritméticas mediante el análisis de los cambios en los parámetros de dificultad del TA o explorar los efectos de diversas condiciones experimentales en las que se puede aplicar el TA como formatos de aplicación informatizados comparados con la versión de lápiz y papel que se ha aplicado en el presente estudio.

El LLTM ha sido el primer modelo de esta clase que ha sido propuesto y quizás por este motivo es el modelo componencial que cuenta con mayor número de aplicaciones empíricas en diversas tareas; sin embargo en las últimas décadas ha ocurrido una explosión de propuestas de modelos psicométrico-cognitivos en los que solo se han desarrollado pocas aplicaciones prácticas. Es pues, de suma importancia que en el futuro se empiecen a desarrollar estudios en los que se apliquen este tipo de modelos en tareas de diversa naturaleza.

El futuro del enfoque psicométrico-cognitivo también se encuentra estrechamente ligado al desarrollo de la psicología cognitiva pues dichos avances permitirán a los psicómetras desarrollar modelos y diseñar instrumentos en los que se conozca de forma más profunda la naturaleza y estructura del constructo que se pretende medir y de esta forma lograr que el proceso evaluativo produzca inferencias válidas sobre el dominio de los examinados sobre los procesos cognitivos involucrados en la solución correcta de las tareas que requiere la prueba.

REFERENCIAS

Alarcón, J. (1994). Libro para el maestro. Matemáticas. Educación secundaria. México: SEP.        [ Links ]

Alonso, J. &  Olea, J. (1997). Modelos de evaluación de los conocimientos matemáticos., Evaluación del conocimiento y su adquisición. Madrid : CIDE.        [ Links ]

Assessment Systems Corporation (1996). Rascal. ST Paul, MN.         [ Links ]

Baker, F. B. (1993). Sensitivity of the linear logistic test model to misspecification of the weight matrix. Applied Psychological Measurement, 17, 201-210.         [ Links ]

Bejar, I. (1990). A generative approach to the modeling of a three-dimensional spatial task. Applied Psychological Measurement, 14 (3), 137-245.        [ Links ]

Bejar, I. (1991). A generative approach to the modeling of isomorphic hidden-figure items. Applied Psychological Measurement, 15 (2), 129-137.         [ Links ]

Bejar, I. & Yocom, P. (1986). A generative approach to the development of hidden-figure items. Research Report Nº RR-150-531. Princeton, NJ: Educational Testing Service.         [ Links ]

Cortada de Kohan, N. (2000). Importancia de la investigación psicométrica. Revista Latinoamericana de Psicología,34 (3), 229-240.         [ Links ]

Dimitrov, D. M. (2007). Least Squares Distance Method of Cognitive Validation and Analysis for Binary Items Using Their Item Response Theory Parameters. Applied Psychological Measurement, 31 (5), 367-387.        [ Links ]

Dimitrov, D. M. & Raykov, T. (2003). Validation of cognitive structures: a structural equation modeling approach. Multivariate Behavioral Research, 38, 1-23.         [ Links ]

Embretson, S. E (1985). Multicomponent Latent Trait Models for Test Design. En S. Embretson (Ed.), Test Design. Developments in Psychology and Psychometrics. New York: Academic Press, Inc.         [ Links ]

Embretson, S. E. (1999). Generating items during testing: psychometric issues and models. Psychometrika, 64, 407-433.         [ Links ]

Embretson, S. E. & Reise, S. (2000). Item Response Theory for Psychologists. London: Lawrence Associates Publishers.         [ Links ]

Fischer, G.H. (1973). The linear logistic test model as an instrument in educational research. Acta Psychologica, 37, 359-374.         [ Links ]

Fischer, G.H. (1995). The linear logistic test model. En G.H. Fischer & I.W. Molenaar (Eds.). Rasch Models: Foundations, recent developments and aplications. New York: Springer-Verlag.         [ Links ]

Fischer, G.H. & Ponocny-Seliger, E. (1998). Structural Rasch modelling, handbook of the usage of LPCM-Win. Holanda: ProGAMMA.         [ Links ]

Fraser, C. (1988). NOHARM: Computer software and manual. Australia: Author.         [ Links ]

Gierl, M.J., Tan, X. & Wang, Ch. (2005). Identifying content and cognitive dimensions on the SAT. Research Report nº 2005-11. College Board.        [ Links ]

Hornke, L. & Habon, M. (1986). Rule-based item bank construction and evaluation within the linear logistic framework. Applied Psychological Measurement, 14 (3), 137-245         [ Links ]

Hughes, M. (1986). Los niños y los números. Barcelona: Planeta.         [ Links ]

Kamii, C. (1989). Reinventando la aritmética II. Madrid: Visor.         [ Links ]

López, A. & Elosua, P. (2002). Formulación y validación de un modelo logístico lineal para la tarea de adición y sustracción de fracciones y números mixtos. Psicothema, 14, 802-809.         [ Links ]

Maza, C. (1999). Enseñanza de la suma y de la resta. Madrid: Síntesis.         [ Links ]

Medina-Díaz, M. (1993). Analysis of cognitive structure using the linear logistic test model and quadratic assignment. Applied Psychological Measurement, 17, 117-130.         [ Links ]

Messick, S. (1984). The psychology of educational measurement. Journal of Educational Measurement, 33, 379-416.         [ Links ]

Mialaret, G. (1984). Las matemáticas: cómo se aprenden, cómo se enseñan. Madrid: Visor.         [ Links ]

Orton, A. (1996). Didáctica de las matemáticas. Madrid: Ediciones Morata, S.A.         [ Links ]

Prieto, G & Delgado, A.R. (1999). Medición cognitiva de las aptitudes. En J. Olea, V. Ponsoda & G. Prieto (Eds.), Test informatizados: fundamentos y aplicaciones. Madrid : Pirámide.        [ Links ]

Real, E., Olea, J., Ponsoda, V., Revuelta, J., & Abad, F.J. (1999). Análisis de la dificultad de un test de matemáticas mediante un modelo componencial. Psicológica, 20, 121-134.         [ Links ]

Revuelta, J. & Ponsoda, V. (1998). Un test adaptativo informatizado de análisis lógico basado en la generación automática de ítems. Psicothema, 10, 753-760.         [ Links ]

Romero, S.J., Ponsoda, V. & Ximénez, C. (2006). Validación de la estructura cognitiva del test de signos mediante modelos de ecuaciones estructurales. Psicothema, 18, 835-840.         [ Links ]

Rouse, S.V., Finger, M.S. & Butcher, J.N. (1999). Advances in clinical personality measurement: An item response theory analysis of the MMPI – PSY- 5 scales. Journal of Personality Assessment, 72, 282-307.         [ Links ]

Rupp, A. & Mislevy, R. (2006). Cognitive Foundations of Structured Item Response Models. En J.P. Leighton & M.J. Gierl (Eds.), Cognitive Diagnostic Assessment: Theories and Applications. Cambridge: Cambridge University Press.         [ Links ]

Tate, R. (2003). A comparison of selected empirical methods for assessing the structure of responses to items. Applied Psychological Measurement, 27, 159–203.         [ Links ]

Van der Linden, W. & Hambleton, R. (1997). Handbook of modern item response theory. New York: Springer.         [ Links ]

Recepción: mayo de 2006
Aceptación final: julio de 2007.