Artículo especial

 

A spreadsheet program for making a balanced Latin Square design^¤

Hoja de cálculo para balancear diseños experimentales del tipo Cuadrado Latino

Planilha eletrônica para balancear delineamentos experimentais de tipo Quadrado Latino

 

Beob G Kim¹, Animal Science, PhD; Hans H Stein¹*, Animal Science, PhD.

¹Department of Animal Sciences, University of Illinois, Urbana, IL 61801, USA

(Recibido: 15 septiembre, 2009; aceptado: 6 octubre, 2009)

 

---

Summary

Latin square designs are often employed in animal experiments to minimize the number of animals required to detect statistical differences. Generally, potential carryover effects are not balanced out by randomization. Systemic methods are available for equalizing the residual effects. We have developed an Excel^® spreadsheet-based program, the Balanced Latin Square Designer (BLSD), to facilitate the generation of Latin squares balanced for carryover effects. The program allows a user to input the number of treatments that is equal to the number of animals and periods in a square. A user may also input the number of squares. Then, the BLSD automatically generates Latin squares balanced for the first order carryover effects. For an even number of treatments, each treatment immediately precedes and follows every other treatment exactly once in the square. For Latin squares with an odd number of treatments, the first order residual effects can be balanced only if they are replicated an even number of times. The program also displays a table for an experimental schedule sorted by period and animal. The BLSD allows animal scientists to quickly and accurately generate Latin squares balanced for the first order carryover effects. The program is freely available upon request.

Key words: animal experiment, carryover effect, Latin square design.

 

---

Resumen

El diseño del tipo “Cuadrado Latino” es muy empleado en experimentación, buscando minimizar el número de animales que se requieren para detectar diferencias estadísticas entre tratamientos. Generalmente, los efectos remanentes potenciales (de arrastre) no se logran balancear mediante la simple aleatorizacion de animales y tratamientos. Existen métodos sistémicos para igualar los efectos residuales. Presentamos acá una aplicación de Excell^® que denominamos Diseñador de Cuadrados Latinos Balanceados (BLSD, por su sigla en Ingles), y que sirve para facilitar la generación de Cuadrados Latinos balanceados para efectos de arrastre. El programa permite al usuario ingresar el número de tratamientos equivalente al número de animales y periodos en un cuadrado. El usuario puede también ingresar el número de cuadrados. Luego, el BLSD automáticamente genera Cuadrados Latinos balanceados para los efectos de arrastre de primer orden. Cuando se trate de un número par de tratamientos, cada tratamiento inmediatamente precede y sobreviene al otro tratamiento exactamente una vez en el cuadrado. Para Cuadrados Latinos con número impar de tratamientos, los efectos residuales de primer orden pueden ser balanceados sólo si son replicados un número par de veces. El programa además ofrece una tabla para experimentos programados por animal y por periodo. El BLSD permite al investigador generar, con precisión y rapidez, Cuadrados Latinos balanceados para los efectos de arrastre de primer orden. El programa se encuentra disponible de forma gratuita para quienes lo soliciten.

Palabras clave: diseño de Cuadrado Latino, efecto de arrastre, experimentos con animales.

 

---

Resumo

O delineamento “Quadrado Latino” é muito utilizado na experimentação, procurando minimizar o número de animais requeridos para detectar diferenças estatísticas significativas entre tratamentos. Geralmente, os efeitos residuais potenciais não podem ser balanceados mediante uma simples aleatorização de animais e tratamentos. Existem métodos sistêmicos para igualar os efeitos residuais. Apresentamos uma aplicação em Excell^® que denominamos “Balanced Latin Square Designer (BLSD)”, que serve para facilitar a geração de Quadrados Latinos para efeitos residuais. O programa permite ao usuário ingressar o número de tratamentos equivalente ao número de animais e períodos em quadrado. O usuário pode também ingressar o número de quadrados. Logo o BLSD automaticamente gera quadrados latinos balanceados para os efeitos residuais de primeira ordem. Quando se tem um número par de tratamentos, cada tratamento imediatamente precede e sucede a outro tratamento exatamente uma vez no quadrado Latino. Para Quadrados Latinos com número impar de tratamentos, os efeitos residuais de primeira ordem podem ser balanceados unicamente, sim é replicado um número par de vezes. O programa também oferece uma tabela para experimentação programada por animal e por período. O BLSD permite ao pesquisador gerar, com precisão e rapidez. Quadrados Latinos balanceados para os efeitos residuais de primeira ordem. O programa encontrase disponível de forma gratuita.

Palavras chave: efeito residual, experimentos com animais, Quadrado Latino.

 

---

Introduction

The Latin square design generally requires fewer subjects to detect statistical differences than other experimental designs. This design is often employed in animal studies when an experiment uses relatively large animals (El-Kadi et al., 2008; Pardo et al., 2008; Seo et al., 2009) or animals requiring surgeries for the study (Dilger and Adeola, 2006; Stein et al., 2009). In a Latin square design, each treatment is assigned once to each row (period) and each column (animal). Although the sequences of rows and columns may be randomized, potential carryover effects are not equalized (Figure 1). In other words, one treatment immediately precedes a certain treatment never or more than once. To balance potential carryover effects, all treatments should be followed by all other treatments equally.

A systemic method is available for balancing the first order residual effects (Williams, 1949). This method is not overly complicated, but it is timeconsuming if an experiment requires a large size of square or multiple squares. Therefore, the Balanced Latin Square Designer (BLSD) is developed to facilitate the generation of Latin squares balanced for carryover effects based on Microsoft Excel ^® that has been widely used in animal science and biological research (Lindemann and Kim, 2007; Kim et al., 2009).

 

 

A systemic method for balanced Latin square designs

The systemic method balances the residual effects when a treatment is an even number. A balanced 6 × 6 Latin square design using this method is illustrated in Figure 2. In this example, treatments A to F are ordinarily assigned in the first row (animal). Treatments for the fi rst column (period) are assigned as an order of:

1, 2, n, 3, n-1, 4, ···, and (n + 2)/2,

And treatments for the second to the last row are assigned using the same sequence as in the first row, but starting with the treatment assigned to the first column (i.e., BCDEFA, FABCDE, CDEFAB, EFABCD, and DEFABC in this example). All treatments are preceded and followed by all other treatments exactly once. The balance of this design is maintained by a randomization of the treatments in the first period before assigning treatments in the other periods or a post randomization by column.

 

 

 

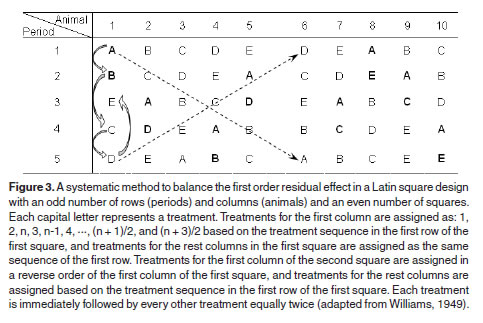
For Latin square designs with an odd number of treatments, the first order residual effects can be balanced only if the square is replicated an even number of times. In Figure 3, a replicated 5 × 5 Latin square design is illustrated. Treatments A to E are ordinarily assigned in the first row. Based on this treatment sequence, treatments for the first column are assigned as an order of:

1, 2, n, 3, n-1, 4, ···, (n + 1)/2, and (n + 3)/2,

And treatments for the second to the last row are assigned using the same sequence as in the first row, but starting with the treatment assigned to the first column (i.e., BCDEA, EABCD, CDEAB, and, DEABC in this example). Treatments for the first column of the second square are assigned in a reverse order of the first column of the first square, and treatments for the remaining columns are assigned based on the treatment sequence in the first row of the first square starting with the treatment assigned to the first column. All treatments are preceded and followed by all other treatments by row exactly twice.

 

 

Program description

Using the method described above, a program is developed to facilitate the generation of Latin squares balanced for immediate carryover effects. The BLSD source codes for all the modules have been written in Visual Basic for Application as an Excel 2003 add-in. A user can run the program file with no special installation. When the file is opened, a user needs to enable macros to use the functions in the BLSD.

For Latin square designs with an even number of treatments, the user inputs the number of treatment that is the same as the number of periods and animals and the number of replicates of squares (Figure 4). The user then clicks the running button to run an allotment. The treatments for the first period are randomly assigned to the animals, and the treatments for the rest periods are systemically assigned as described in Figure 2. Additionally, an experimental schedule is tabulated on the bottom of the sheet. This schedule is sorted by periods and animals, and respective sample numbers are assigned. If treatment names other than alphabetical letters are preferred, a user may change the treatments in the first period of the Latin square. A user may also use the Numeric Treatment tab to assign treatments as numbers.

For Latin square designs with an odd number of treatments, the square should be replicated an even number of times to balance the first order carryover effects. In the example in Figure 5, treatments are assigned as described in Figure 3 after randomizing the treatments in the first period of the first square. The sequentially assigned treatment numbers may be updated changing the first treatment number. If a user input an odd number of treatments and an odd number of replicates of squares, the program still runs but the immediate carryover effects are not balanced.

For an incomplete Latin square design, such as a 10 × 7 Latin square design with 10 treatments, 10 animals, and 7 periods, a user may run the BLSD as 10 × 10 and use the first 7 periods in the allotment result. In this case, the immediate carryover effects are not perfectly balanced, but the imbalance is minimized as every treatment immediately precedes and follows another treatment no more than once.

Although the BLSD balances the first order carryover effects, the program does not balance remote (second, third, fourth, etc.) carryover effects. A method developed by Alimena (1962) minimizes the imbalance of remote carryover effects. However, this method can be used only when the number of treatment is a prime number minus one (e.g., 2, 4, 6, 10, 12, 18, 22, etc.), and the remote carryover effects are not perfectly balanced. In most animal research, balancing immediate carryover effects is sufficient.

 

Conclusion

We have developed the BLSD to allow animal scientists to generate Latin squares balanced for the first order carryover effects in a quick and accurate manner. The program is freely available upon request to the corresponding author.

 

 

References

Alimena BS. A method of determining unbiased distribution in the Latin square. Psychometrica 1962; 27:315-317.         [ Links ]

Dilger RN, Adeola O. Estimation of true phosphorus digestibility and endogenous phosphorus loss in growing pigs fed conventional and low-phytate soybean meals. J Anim Sci 2006; 84:627-634.         [ Links ]

El-Kadi SW, McLeod KR, Elam NA, Kitts SE, Taylor CC, Harmon DL, Bequette BJ, Vanzant ES. Nutrient net absorption across the portal-drained viscera of forage-fed beef steers: Quantitative assessment and application to a nutritional prediction model. J Anim Sci 2008; 86:2277-2287.         [ Links ]

Kim BG, Lindemann MD, Bridges PJ, Ko C. GEPRO: Gene expression profiler for microarray data. Rev Colomb Cienc Pecu 2009; 22:12-18.         [ Links ]

Lindemann MD, Kim BG. Technical note: A model to estimate individual feed intake of swine in group feeding. J Anim Sci 2007; 85:972-975.         [ Links ]

Pardo O, Carulla JE, Hess HD. Effect of protein and energy relationship on the levels of ammonium rumen and blood urea nitrogen and milk, in dual purpose cows at the llanero foothills, Colombia. Rev Colomb Cienc Pecu 2008; 21:387-397.         [ Links ]

Seo S, Kim HJ, Lee SY, Ha JK. Nitrogen utilization of cell mass from lysine production in goats. Asian-Aust J Anim Sci 2008; 21:561-566.         [ Links ]

Stein HH, Connot SP, Pedersen C. Energy and nutrient digestibility in four sources of distillers dried grains with solubles produced from corn grown within a narrow geographical area and fed to growing pigs. Asian-Aust J Anim Sci 2009; 22:1016-1025.         [ Links ]

Williams EJ. Experimental designs balanced for the estimation of residual effects of treatments. Aust J Sci Res 1949; A2:149-168.         [ Links ]