ARTÍCULO ORIGINAL

 

Application of the principal–component analysis in the evaluation of three grass varieties^¤

 

Aplicación del análisis por componentes principales en la evaluación de tres variedades de pasto

 

Aplicação da análise de componentes principais na avaliação de três variedades de capim

 

 

Luis F Restrepo^1*, Esta, Esp; Sandra L Posada¹, Zoot, PhD; Ricardo R Noguera¹, Zoot, PhD.

 

* Autor para correspondencia: Luis F Restrepo. Facultad de Ciencias Agrarias. Universidad de Antioquia. AA 1226, Medellín Colombia. E–mail: frbstatistical@yahoo.es

¹ Grupo de Investigación en Ciencias Agrarias–GRICA, Facultad de Ciencias Agrarias, Universidad de Antioquia, AA 1226, Medellín, Colombia.

 

(Recibido: 5 agosto 2011; aceptado: 17 abril 2012)

 

 

---

Summary

Objective: demonstrate how to use the principal–component analysis to reduce dimensionality in assessing three varieties of Ryegrass (Lolium sp. L.), namely, tetraploid hybrid (Foster), annual diploid (Southern Star), and annual tetraploid (Beefbuilder). Both the statistical properties and programming using the SAS statistical package are also highlighted. Results: The variables that defined the main factor for the three grass varieties were: height from the floor, middle width of the fully elongated last leaf, and biomass.

Key words: dimensionality, eigenvalue, factor, grass growth.

---

Resumen

Objetivo: mostrar una aplicación del análisis de componentes principales en la reducción de la dimensionalidad de variables derivadas de la evaluación agronómica de tres variedades de pasto. Métodos: los pastos evaluados fueron Ryegrass (Lolium sp. L.), híbrido tetraploide (Foster), anual diploide (Southern Star) y anual tetraploide (Beef Builder). Igualmente se destacan las propiedades estadísticas y la forma de programación en el paquete estadístico SAS. Resultados: se observó que las variables que definieron el factor principal para las tres variedades fueron: altura desde el piso, ancho de la parte media de la última hoja completamente elongada y biomasa.

Palabras clave: crecimiento vegetal, dimensionalidad, factor, valor propio.

---

Resumo

O objetivo principal deste trabalho foi mostrar uma aplicação da análise de componentes principais na redução da dimensionalidade de variáveis derivadas da avaliação agronômica de três variedades de capim azevém (Lolium sp. L), a saber, híbrido tetraplóide (Foster), anual diplóide(Southern Star) e anual tetraploide (BeefBuilder). Também se destacam as propriedades estatísticas e a programação no pacote estatístivo SAS. Resultados: como um resultado notável do processo de pesquisa foi observado que as variáveis que definiram o principal fator para as três variedades foram: altura do solo, a largura da parte meia da última folha totalmente alongada e a biomassa.

Palavras chave: crescimento vegetal, dimensionalidade, fator, autovalor.

---

 

 

Introducción

El análisis de componentes principales transforma un conjunto de variables correlacionadas en un nuevo conjunto de variables no correlacionadas (Almenara et al., 1998). El objetivo del análisis es reducir la dimensionalidad en la cual se expresa el conjunto original de variables (Peña, 2002).

El análisis multivariado de componentes principales es una técnica que permite clasificar la variación fenotípica en sistemas independientes de caracteres correlacionados (Di Masso et al., 2010). El Análisis de Componentes Principales se utiliza con el objetivo de establecer patrones de comportamiento en los sistemas ecológicos (Torriente y Torres, 2010). Posee gran importancia en el campo agropecuario con el fin de explicar la variabilidad relacionada con la morfometría de los animales, factores de producción animal, análisis y evaluación de pastos y forrajes, evaluación de la calidad de leche y de la carne, aspectos ambientales relacionados con el hato, evaluación de la calidad del agua para implementaciones piscícolas, entre una gama de aplicaciones.

En 1901 Karl Pearson publicó un trabajo sobre el ajuste de un sistema de puntos a una línea o a un plano en un multiespacio (Pla, 1986). El enfoque de Pearson fue retomado en el año 1933 por Hotelling, quien en primera instancia formuló el análisis de componentes principales (Del Ángel, 2004). La investigación de Pearson se centró en aquellos componentes o combinaciones lineales de variables originales para las cuales se genera un plano, donde el ajuste del sistema de puntos debe poseer la mínima suma de las distancias de cada punto al plano de ajuste.

Hotelling se centró en el análisis de los componentes que sintetizan la mayor variabilidad del sistema de puntos. Lo anterior explica el calificativo de principal. Cada punto en el multiespacio p–dimensional es el extremo de un vector, de tal modo que cada uno de sus elementos es una de las i–ésima variables en un individuo dado. El objetivo es buscar el eje más largo de la nube de puntos, colocado en un espacio de dimensiones referido a las variables. Este es el eje que explica la mayor variación entre individuos. De igual forma conserva la menor distancia euclidiana; este eje es el primer componente principal. El segundo eje que se busca debe ser perpendicular al primero, que a su vez explique la segunda mayor variación entre individuos. Este constituye el segundo componente principal. Esta es la manera como se puede establecer hasta el p–ésimo componente principal, con el objetivo general de reemplazar el espacio p–dimensional en un nuevo espacio reducido de k dimensiones, con k<p. Las coordenadas de cada punto pueden ser calculadas dentro de este nuevo espacio. En síntesis, con pocas componentes se puede explicar lo que acontece en el espacio original p–dimensional. El objetivo del análisis de componentes principales es reducir grandes cantidades de datos por medio de pocos parámetros (Dallas, 2000).

Método R Y ∑

Los componentes principales generados a partir del método R y ∑, en general, no son los mismos; entendiéndose por método R el que emplea la matriz de correlación, y por método ∑ el que utiliza la matriz de varianzas y covarianzas (Figura 1).

No es posible pasar del sistema R al ∑ o viceversa por simple ordenación de los factores. Si las unidades de medida de las variables son distintas (años, kilogramos, metros, etc.) es preferible el uso de R porque equivale a utilizar variables reducidas y, por tanto, sin dimensión física. Pero si las unidades de medida son las mismas, o razonablemente conmensurables, es preferible realizar el análisis sobre ∑, que es menos artificial. También es recomendable utilizar ambas matrices y comparar las interpretaciones de las dos clases de componentes obtenidas (Carmona et al., 2000).

El método de la covarianza tiene interés estadístico, ya que la componente principal i–ésima es la combinación lineal de las respuestas que explican la posición i–ésima más grande de la variabilidad total y la maximización de tal varianza de resultados estándar posee una característica artificial. Como Anderson (2003) demostró, la teoría de muestreo de componentes generados a partir de la matriz de correlación (método R) es más compleja que las derivadas por medio de la matriz de varianzas y covarianzas ∑.

En la matriz de correlación R, los valores de la diagonal principal son iguales a uno (Cuadras, 2010). Adicionalmente, las nuevas variables estandarizadas poseen varianza unitaria. Esto significa que en el nuevo conjunto de datos a partir del cual se generan los componentes principales se otorga la misma importancia a todas las variables tenidas en cuenta. El empleo de la matriz de correlación implica una ponderación de las variables originales otorgándoles a cada una la misma importancia, independientemente de los valores relativos de sus varianzas.

Por todo lo anterior es de vital interés examinar cuidadosamente la naturaleza de las variables, y por ende el tipo de observación, con el fin de decidir que método aplicar R o ∑, que cambio de escala puede introducirse antes de establecer R o ∑, y que interpretación deberá darse a los componentes encontrados.

Obtención de los componentes principales

La obtención de los CP puede realizarse por varios métodos alternativos:

1. Buscando aquella combinación lineal de las variables que maximiza la variabilidad.

2. Buscando el subespacio de mejor ajuste por el método de los mínimos cuadrados, minimizando la suma de cuadrados de las distancias de cada punto al subespacio.

3. Minimizando la discrepancia entre las distancias euclidianas de los puntos calculados en el espacio original y en el subespacio de baja dimensión.

4. Mediante regresiones alternadas, usando el método Biplot.

Selección del número de componentes

En el análisis por componentes principales es necesario calcular e interpretar tanto los valores propios generados, como los vectores propios. Se debe establecer cuantos valores propios deberán considerarse, a fin de reducir la dimensionalidad en la cual se expresan las observaciones.

Cada componente principal explica una proporción de la variabilidad total y ésta se calcula mediante el cociente entre el valor propio y la traza de la matriz de covarianza. Se denomina proporción de la variabilidad total explicada por el k–ésimo componente.

Al decidir cuántos componentes se manifiestan en una situación particular, deberá examinarse cuantos componentes son necesarios incluir para que el porcentaje de variación explicada sea satisfactorio. Kaiser (1960) propone un criterio para seleccionar el número de componentes principales, el cual consiste en incluir sólo aquellos componentes cuyos valores propios sean superiores al promedio; la desventaja es que tiende a incluir muy pocos componentes cuando el número de variables es inferior a veinte.

Existe otro criterio, denominado gráfico de Cattell (1966) o de saturación de los componentes. El cual consiste en elaborar un gráfico donde se represente el porcentaje de variación explicada por cada componente en la ordenada y expresar los componentes en orden decreciente en la abscisa.

Existe otro criterio citado por Cuadras (2010), donde se afirma que el número de componentes se toma de modo que P máximo sea próximo a un número especificado por el investigador o usuario.

Debe tenerse en cuenta que el análisis de componentes principales también permite algunas subjetividades por parte de quien lo usa, tanto en el número de componentes a elegir, como del peso de las variables. Esto se da de acuerdo con la experiencia del investigador, quien determina las componentes que realmente explican el fenómeno.

Características de los componentes

1. Sean dos nubes de puntos (representadas como en la figura 2 por elipsoides que las rodean). La varianza es una medida de la dispersión. Las variables X, Y tienen ambas la misma varianza en el caso de la elipse y del círculo, pero la covarianza en el círculo es cero y la de la elipse es más o menos alta, y positiva.

2. No hay correlación entre los componentes principales (Cuadras, 2010).

3. Si se puede establecer una distribución normal multivariada en los datos originales, entonces son independientes.

4. Cada componente principal sintetiza la máxima variabilidad residual contenida en los datos, pudiéndose estimar el número de grupos o clases sobre el conjunto de datos (Tibshirani et al., 2001).

2. No hay correlación entre los componentes principales (Cuadras, 2010).

3. Si se puede establecer una distribución normal multivariada en los datos originales, entonces son independientes.

4. Cada componente principal sintetiza la máxima variabilidad residual contenida en los datos, pudiéndose estimar el número de grupos o clases sobre el conjunto de datos (Tibshirani et al., 2001).

5. Cada una de las variables posee cierto grado de asociación con el componente principal, donde la relación puede ser directa, o inversamente proporcional.

6. Si se trabaja con datos estandarizados, las componentes principales se obtienen de la diagonalización de la matriz de correlaciones. Se utilizarán datos estandarizados cuando las escalas de medida de las variables sean muy diferentes.

7. Debe existir relación entre las variables originales (De Vicente et al., 1999) con el fin de que tenga sentido el análisis de componentes principales.

8. Para su interpretación, en el análisis de componentes principales se deben excluir aquellas variables que no tengan relación con los componentes.

9. Los componentes principales se deben explicar a partir de las variables que tienen relación con el factor.

10. Se sugiere transformar las variables originales correlacionadas en nuevas variables no correlacionadas que puedan ser interpretadas (Peña, 2002).

11. El análisis de componentes es aplicable a variables cuantitativas, pudiéndose suplementar con variables cualitativas.

12. Los componentes principales son ortogonales (Cuadras y Fortiana, 2000).

13. Los componentes principales denotan interacción entre individuos y factores. la

14. Los componentes principales se pueden rotar. Además, el análisis de regresión se puede utilizar como método para el descarte de variables (Mardia et al., 1979)

15. El análisis por componentes permite generar planos en los cuales se puede apreciar la interacción entre las variables y entre éstas con los componentes. Se puede emplear rotación ortogonal, en la que los ejes se mantienen formando un ángulo de 90 grados; cuando no se limita a ser ortogonal, la rotación se denomina oblicua (Hair et al., 1999).

16. Por medio del análisis de componentes principales el investigador puede detectar que variables pueden explicar de mejor forma ciertos fenómenos. El análisis permite estudiar la relación entre individuos y la interacción que éstos tienen con las variables.

17. En términos geométricos, el jésimo subespacio lineal atravesado por los primeros jésimos componentes principales proporciona el mejor ajuste posible de los puntos de datos, medidos por la suma de los cuadrados de las distancias perpendiculares desde cada vector de datos para el subespacio. Esto está en contraste con la interpretación geométrica de regresión por mínimos cuadrados, lo que minimiza la suma de los cuadrados de las distancias verticales (SAS STATS, 1999).

18. Se emplea para agrupar las unidades experimentales en subgrupos, de tal manera que exista homogeneidad al interior de cada clúster (Figura 3). El análisis de componentes principales es un criterio fundamental para hacer conjeturas sobre el número de factores que se deben determinar en el análisis factorial y para probar si, en realidad, un grupo de variables p > 2 cae dentro de un espacio de dos o tres dimensiones que permita ser observado dentro del análisis de clúster (Cuadras, 2010).

En el análisis de componentes principales se puede efectuar análisis Biplot, el cual es una técnica que permite la representación en un mismo gráfico de las filas (individuos) y las columnas (variables) de una matriz de datos (Gower et al., 2011).

Rotaciones

VARIMAX. Es recomendable cuando existen pocos componentes principales, el objetivo de este método es lograr que cada componente presente altas correlaciones.

PROMAX. Se recomienda aplicarlo sobre un análisis VARIMAX previo.

QUARTIMAX. El objetivo es lograr que cada variable tenga alta correlación con muy pocos componentes principales cuando existe un número alto de estos componentes.

 

Materiales y métodos

En un hato lechero ubicado en el municipio de San Pedro de los Milagros, altiplano norte antioqueño, fue evaluado el establecimiento de tres variedades de pasto Ryegrass (Lolium sp. L.). El municipio de San Pedro de los Milagros presenta una temperatura media de 14 ºC, humedad relativa del 72%, precipitación media anual de 1.500 mm y se encuentra a 2.475 msnm, lo que permite clasificarlo en una zona de vida Bosque Húmedo Montano Bajo (BhMB), de acuerdo con la clasificación de (Holdridge, 1967).

Las tres variedades de pasto, correspondientes a un híbrido tetraploide (Foster), un anual diploide parcelas/variedad), de acuerdo con el esquema que se presenta en la figura 4.

Una vez realizado el primer pastoreo, las evaluaciones agronómicas se realizaron cada 35 días, hasta el cuarto pastoreo. En cada ocasión de medida se evaluó la biomasa (kg MS/m²) y el porcentaje de establecimiento (%). Además se tomó información de cinco plantas/parcela en lo correspondiente a: 1) altura desde el piso (cm), 2) longitud de la última hoja completamente elongada (cm), 3) ancho de la parte media de la última hoja completamente elongada (cm), 4) número de hojas por planta (por tallo), y 5) relación hoja: tallo (g/g). Un análisis de componentes principales fue desarrollado para reducir la dimensionalidad de las variables inmersas en un plano multidimensional. Cabe anotar que se tomaron igual número de subparcelas dentro de cada parcela principal a fin de generar la información.

Metodología estadística

Se empleó el análisis de componentes principales por el método R debido a la naturaleza de las variables, utilizando como criterio de selección de componentes el criterio de Kaiser. El programa estadístico utilizado fue SAS.

Programación en el paquete estadístico A

DATA Z;

INPUT A B C D E F G;

CARDS;

DATOS

;

PROC PRINCOMP OUT=SALIDA;

VAR A B C D E F G;

TITLE2 ‘PLOT OF THE FIRST TWO PRINCIPAL

COMPONENTS'

%PLOTIT(DATA=SALIDA, LABELVAR=FACTOR,

PLOTVARS=PRIN2 PRIN1, COLOR=BLACK,

COLORS=BLUE);

RUN;

 

Resultados

En la tabla 1 se muestran los dos primeros componentes principales por cada tipo de variedad, destacándose que las variables que definen el factor principal para las tres variedades fueron básicamente: Altura desde el piso, ancho de la parte media de la última hoja completamente elongada y biomasa. El componente principal dos se define básicamente a través de la variable porcentaje de establecimiento.

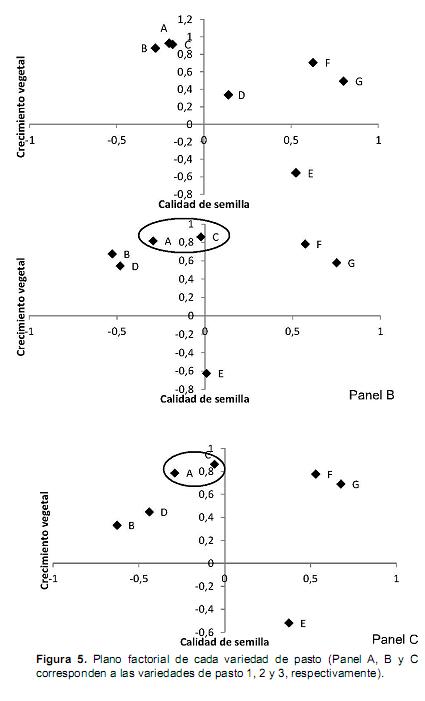
En la figura 5 se presenta el plano factorial para cada una de las variedades evaluadas.

Durante el trabajo de campo se obtuvieron ocho variables, identificadas desde la A hasta la G. A partir del análisis de componentes principales fue posible sintetizar la información o reducir el número de variables. La denominación de los componentes principales fue deducida tras observar la relación de ellos con las variables iniciales, de tal forma que a partir de variables observables se obtuvieron variables no observables o componentes. Las variables no observables generadas se denominaron crecimiento vegetal y calidad de la semilla, las cuales representaron el primer y segundo componente principal, respectivamente. En la tabla 1, los componentes principales se representan en forma de matriz, con tantas columnas como componentes principales y tantas filas como variables observables (iniciales). Cada elemento de esta matriz constituye los coeficientes factoriales de las variables, es decir, las correlaciones entre las variables iniciales y los componentes principales, anotando que las componentes son de tipo ortogonal.

Los dos componentes principales seleccionados (crecimiento vegetal y calidad de la semilla) fueron los que explicaron la mayor parte de la variación total contenida en los datos originales, como se muestra en la tabla 2.

El primer componente principal (crecimiento vegetal) fue el que reunió la mayor proporción de la variabilidad original, representada en todas las variedades de pasto por tres variables en común, a saber, altura desde el piso (A), ancho de la parte media de la última hoja completamente elongada (C) y biomasa (F), que fueron las de mayor coeficiente factorial. El segundo componente principal (calidad de la semilla) aglutinó la variación no reunida por el primero, con una única variable original (porcentaje de germinación) presentando los mayores coeficientes factoriales. En el análisis de componentes principales, los nuevos factores (o componentes) forman un ángulo de 90 grados y deben ser independientes entre sí; esto es, una variable debe tener coeficientes elevados con un sólo factor y no deben existir factores con coeficientes similares.

Para la representación gráfica de los puntos– variable se tomaron como ejes de coordenadas los componentes principales, como se observa en la figura 5. Cada punto–variable está representado por la coordenada que le corresponde a esa variable en cada uno de los componentes principales, así, la coordenada de un punto sobre un eje es igual a la correlación de esa variable respecto a ese eje. Por ejemplo, en la figura 5 (panel A, B y C) se observa que las variables altura desde el piso (A), ancho de la parte media de la última hoja completamente elongada (C) y biomasa (F) fueron las que más contribuyeron en la formación del eje de las abscisas (eje Y o componente principal 1), en tanto que esas mismas variables estuvieron poco relacionadas con el componente principal 2, dada su mayor cercanía con el origen (valor cero en el eje de las ordenadas o eje X). En todas las variedades de pasto, el punto–variable F (biomasa) fue el que tuvo una mayor contribución en la formación del componente principal 2.

En la figura 5 (panel A, B y C) es posible observar las interrelaciones existentes entre los puntos–variables, esto es, puntos–variables más próximos entre sí tienen mayor grado de correlación. En el panel A, B y C se observa que las variables altura desde el piso (A) y ancho de la parte media de la última hoja completamente elongada (C) presentan un mayor grado de correlación entre ellas, que con el punto–variable F (biomasa). La elevada correlación entre las variables le da sentido al análisis, ya que indica la existencia de información redundante y permite que pocos factores (o componentes principales) expliquen gran parte de la variabilidad total. Finalmente, se destaca la similitud en comportamiento de las variables A y C respecto el componente principal 2. Los valores negativos no presentan coherencia biológica, toda vez que plantas que presenten mayor calidad de la semilla (semilla pura y viable) presentarán mayor porcentaje de germinación y por tanto un mayor crecimiento vegetal.

 

Discusión

En la evaluación de variedades de pasto, resulta de bastante interés conocer cómo se comporta cada variedad en particular en un ecosistema. El análisis de componentes principales permitió conocer los componentes que sintetizan la variabilidad total asociada a un multiespacio, determinándose dos componentes de tipo ortogonal que resumen en un gran porcentaje la dinámica de comportamiento de cada variedad empleada, híbrido tetraploide (Foster), anual diploide (SouthernStar) y anual tetraploide (BeefBuilder). El componente principal se explica básicamente por las variables altura desde el piso, ancho de la parte media de la última hoja completamente elongada y biomasa. Lo anterior se explica debido a que cada variedad de pasto se desarrolla tratando de alcanzar la mayor altura, lo cual se correlaciona con el ancho que alcanza cada una de las hojas.

Se observa que el pasto desarrolla el sistema radicular dependiendo de las condiciones del suelo y gasta gran energía potencializando el desarrollo vegetativo expresado en variables asociadas con la altura y con el desarrollo morfométrico de las hojas. Las plantas transforman la energía radiante del sol en energía química a través de la fotosíntesis y parte de esa energía química queda almacenada en forma de materia orgánica (biomasa). En los resultados derivados del análisis se encontró que el primer componente se explica por el crecimiento del pasto. En el segundo componente la variable que básicamente repercutió fue el porcentaje de establecimiento, denominando al factor o componente como calidad de la semilla. La variedad híbrido tetraploide (Foster) presentó el mayor porcentaje de variabilidad explicado a partir de los componentes elegidos con un 72.86%, la variedad anual tetraploide (BeefBuilder) fue la de menor porcentaje de variabilidad explicado con un 65.41%.

Mediante el análisis de componentes principales se concluyó que las tres variedades de pasto Ryegrass (híbrido tetraploide, anual diploide y anual tetraploide) presentaron comportamiento similar en los componentes que explican la mayor variabilidad asociada al multiespacio, donde las variables que explican cada factor son semejantes en cada variedad.

 

Referencias

1. Almenara J, González JL, García C, Peña P. ¿Qué es el análisis de Componentes principales? Jano 1998; 1268:58–60.         [ Links ]

2. Anderson TW. An Introduction to Multivariate Statistical Analysis. 3th ed. New York: Wiley Series in Probabilityand Statistics; 2003.         [ Links ]

3. Carmona F, Cuadras CM, Oller JM. Representación de datos multivariantes en dimensión reducida. Departamento de Estadística Universidad de Barcelona 2000; [Fecha de acceso: 18 de mayo de 2011] URL: http://www.ub.edu/stat/docencia/ Mates/multivariant.pdf.         [ Links ]

4. Cattell R. The screen test for the number of factors. Multivariate Behavioral Research 1966; 1:245–276.         [ Links ]

5. Cuadras CM, Fortiana J. The Importance of Geometry in Multivariate Analysis and some Applications. In: Rao CR, Szekely G, editors. Statistics for the 21st Century. Methodologies for Applications of the Future. New York: Marcel Dekker; 2000. p.93–108.         [ Links ]

6. Cuadras CM. Nuevos Métodos de análisis multivariante. Barcelona: CMC Editions; 2010.         [ Links ]

7. Dallas JE. Métodos multivariados aplicados al análisis de datos. México: Thomson Paraninfo S.A.; 2000.         [ Links ]

8. De Vicente MA, Bassa JM, Jiménez FJB. Análisis Multivariante para las Ciencias sociales. Madrid: Dykinson; 1999.         [ Links ]

9. Del Ángel NV. Una aplicación del algebra lineal a la estadística (componentes principales) 2004; [Fecha de acceso: 2 de mayo de 2011]. URL: http://www.uv.mx/facmate/licenciatura/tesis_ presentadas/Del_Angel_Cruz_Natalia_Vanessa.pdf.         [ Links ]

10. Di Masso RJ, Pippa C, Silva OS, Font MT. Componentes principales como fenotipos de sistemas biológicos complejos. Relación músculo–hueso en el ratón (Mus musculus).BAG, J Basic Appl Genet 2010; 21:1852–1857.         [ Links ]

11. Gower J, Lubbe SG, Gardner S, Le Roux N. Understanding Biplots. United Kingdom: John Wiley & Sons Ltd; 2011.         [ Links ]

12. Hair J, Anderson R, Tatham R, Black W. Análisis multivariante. Madrid: Prentice Hall; 1999.         [ Links ]

13. Holdridge LR. Life Zone Ecology. Tropical Science Center. San José, Costa Rica; 1967.         [ Links ]

14. Kaiser HF. The application of electronic computers to factor analysis. Educational and Psychological Measurement 1960; 20:141–151.         [ Links ]

15. Mardia KV, Kent JT, Bibby JM. Multivariate Analysis. New York: Academic Press; 1979.         [ Links ]

16. Peña D. Análisis de datos multivariados. Madrid: McGraw Hill; 2002.         [ Links ]

17. Pla LE. Análisis Multivariado: Método de Componentes Principales. Washington: Organización de Estados Americanos; 1986.         [ Links ]

18. SAS Institute Inc., SAS/STAT^® User's Guide, Version 8, Cary, NC: SAS Institute Inc., 1999.         [ Links ]

19. Tibshirani R, Walther G, Hastie T. Estimating the number of clusters in a data set via the gap statistic. J R Statist Soc B 2001; 63:411–423.         [ Links ]

20. Torriente D, Torres V. El análisis de componentes principales en la interpretación de sistemas agroecológicos para el manejo de rizo bacterias promotoras del crecimiento vegetal para el cultivo de la caña de azúcar.IDESIA 2010; 28:23–32.         [ Links ]

 

Notas

^¤ Para citar este artículo: Restrepo L, Posada S, Noguera R. Aplicación del análisis por componentes principales en la evaluación de tres variedades de pasto. Rev Colomb Cienc Pecu 2012; 25:258–266..