ORIGINAL ARTICLES

Estimation of growth in intact grazing Holstein steers^¤

Estimación del crecimiento en terneros enteros Holstein en pastoreo

Estimativa do crescimento de novilhos da raça Holandesa em pastejo

Raúl Velásquez Vélez^1*, Zoot, MSc; Ricardo R Noguera², Zoot, MSc, PhD; Sandra L Posada², Zoot, MSc, PhD; Alvaro Hoyos Velásquez², Zoot; Juan Manuel Cerón³, Zoot.

* Corresponding author: Raúl Velásquez Vélez. Departamento de Producción Animal, Facultad de Ciencias Agrarias, Universidad Nacional de Colombia, Medellín, Colombia. Tel: (054) 430 91 31. E-mail: ravelasquezv@unal.edu.co

¹ Departamento de Producción Animal, Facultad de Ciencias Agrarias, Universidad Nacional de Colombia, Medellín, Colombia.

² Grupo de Investigación en Ciencias Agrarias- GRICA, Facultad de Ciencias Agrarias, Universidad de Antioquia, AA 1226, Medellin, Colombia.

³ Cooperativa Lechera de Antioquia (COLANTA), Medellin, Colombia.

(Received: February 13, 2012; accepted: October 13, 2012)

Summary

Background: animal growth does not follow a linear pattern. Accordingly, fitted non-linear models are used to analyze the relationship between growth rate and age. Objective: to assess the ability of several mathematical models (Gompertz, Brody, and von Bertalanffy) to describe growth and development patterns of grazing Holstein males (Bos taurus). Methods: twenty eight intact Holstein steers (average weight 203.8 ± 37.5 kg) were used in the study. The animals grazed on Kikuyu grass pastures (Pennisetum clandestinum) and were supplemented with 1 kg dry matter of reconstituted grain silage until weight reached 301.9 ± 47.9 kg. Animals were weighed at the beginning of the experiment and monthly thereafter from 14 to 21 months of age. The Marquardt's iterative algorithm of PROC NLIN procedure for non-linear models available in the SAS software was used to fit the data to each model and estimate the parameters. Results: Brody model reached the highest estimated value for adult weight (1,097.6 kg) while the Gompertz model displayed the lowest value (795 kg). Bertalanffy model indicated the lowest estimate for maturity index (0.0028) while the highest estimate was obtained by Gompertz (0.0047), being statistically different (p<0.05). Conclusions: Gompertz model best described growth of intact Holstein steers under rotational grazing and feed supplementation.

Key words: Brody, dairy steers, Gompertz, mathematical models, von Bertalanffy.

Resumen

Antecedentes: los animales en crecimiento no siguen un patrón lineal; así que para describir este patrón se necesitan modelos no lineales ajustados, que analicen la relación entre la velocidad de crecimiento y la edad del animal. Objetivo: evaluar los modelos matemáticos Gompertz, Brody y von Bertalanffy de acuerdo con su capacidad para describir el patrón de crecimiento y desarrollo de los machos Holstein (Bos taurus) en pastoreo. Métodos: el estudio experimental se realizó con 28 novillos enteros de raza Holstein, con peso vivo promedio de 203,8 ± 37,5 Kg. Los animales permanecieron en pastoreo rotacional de pasto kikuyo (Pennisetum clandestinum) y fueron suplementados con 1 Kg de materia seca de silo de grano reconstituido hasta alcanzar un peso promedio de 301,9 Kg. ± 47,9 Kg. Los animales fueron pesados al inicio del experimento y luego con intervalos de 30 días, obteniendo información desde los 14 hasta los 21 meses de vida. El ajuste de los datos a cada modelo y las estimativas de los parámetros se realizaron por medio iterativo del algoritmo Marquardt del procedimiento para modelos no lineales PROC NLIN de SAS. Resultados: el modelo Brody alcanzó el mayor valor estimado para el parámetro ''peso maduro'' (1097, 6 Kg) y el modelo Gompertz obtuvo el menor valor (795 Kg). El modelo de Bertalanffy presentó el menor estimativo del parámetro ''índice de madurez'' (0,0028), mientras que el mayor estimativo lo presentó el modelo de Gompertz (0,0047), mostrando diferencia significativa (p<0,05). Conclusiones: el modelo de Gompertz fue el que mejor describió el patrón de crecimiento de los machos Holstein en pastoreo rotacional con suplementación.

Palabras clave: Brody, Gompertz, modelos matemáticos, novillos de lechería, von Bertalanffy.

Resumo

Antecedentes: os animais no seu crescimento não seguem um patrão lineal, pelo qual são necessários modelos matemáticos não lineais, que estudem a relação entre a taxa de crescimento e a idade do animal. Objetivo: avaliar os modelos Gompertz, Brody e von Bertalanffy na sua capacidade para descrever o crescimento de machos inteiros da raça holandês em condições de pastejo. Métodos: o estudo foi realizado com 28 animais não castrados da raça holandês, cujo peso vivo ao inicio do experimento foi de 203,8 ± 37,5 Kg. Os animais foram mantidos em um sistema de pastejo rotacionado com capim kikuyu (Pennisetum clandestinum) e suplementados com 1 Kg de matéria seca de silagem de grão reconstituído até atingir um peso médio de 301,9 ± 47,9 Kg. Todos os animais foram pesados ao inicio do experimento e depois a intervalos de 30 dias, obtendo informação entre os 14 e 21 meses de vida. O ajuste dos dados a cada modelo e as estimativas dos parâmetros foram realizadas com o procedimento PROC NLIN do SAS. Resultados: o modelo Brody atingiu o maior valor estimado para o parâmetro ''peso à maturidade'' (1097,6 Kg) e o modelo Gompertz obteve o menor valor (795 Kg). O modelo von Bertalanffy apresentou a menor estimativa do parâmetro ''índice de maturidade'' (0,0028) entanto que o maior valor foi encontrado no modelo Gompertz (0,0047) (p<0,05). Conclusões: o modelo Gompertz foi o que melhor descreveu o crescimento de machos da raça Holandês mantidos em condições de pastejo rotacionado com suplementação.

Palabras chave: Brody, Gompertz, modelos matemáticos, novilhos de origem leiteira, von Bertalanffy.

Introduction

Specialized dairy systems in Colombia consider beef as a byproduct of milk production. COLANTA's packing plant (FRIGOCOLANTA meat packing plant; Cooperativa Lechera Colanta, Medellin, Colombia) processes more than 50,000 calves per year, averaging 4 days of age, 45 kg body weight, and USD $40 to $50 market value; carcass yield does not exceed 45%. Breeding, fattening, and rearing of those animals would yield 8000 tons of additional meat to the country, representing an additional income of nearly USD $23.5 million (Cerón, 2011).

Animal growth does not follow a linear pattern, so fitted non-linear models are needed to establish the relationship between growth rate and animal age in order to generate a growth curve (Souza et al., 1994). Animal growth models have a sigmoidal shape in which the following phases can be differentiated: a) Acceleration phase: ideally should have its origin at point (0,0) and is characterized for a rapid and positive growth rate peaking at the inflection point of the curve; b) Deceleration phase: begins at the inflection point and occurs where growth rate begins to decrease due to a number of physiological factors that hinder growth; c) Linear phase: when the animal stops growing or when growth is directed towards tissue replenishment (Noguera et al., 2008).

The Gompertz (Winsor, 1932), Brody (Brody, 1945), and von Bertalanffy (von Bertalanffy, 1957) mathematical models are among the most frequently used functions for describing the growth of flora and fauna. Those models include three parameters, two of which have a biological interpretation, and a third representing a mathematical constant. Parameter A is the asymptotic weight or adult weight, and represents the estimated weight at a certain age. Parameter K is the maturity index or the earliness of maturity estimate (Nobre et al., 1987). The greater the K parameter, the greater the prematureness of the animal, and vice versa (Brown et al., 1976). Parameter B is called integration parameter and has no biological meaning.

The aim of this study was to evaluate Gompertz, Brody, and von Bertalanffy mathematical models in their ability to describe growth and development of intact grazing Holstein steers (Bos taurus).

Materials and Methods

Sources of information

The data used in this study included weight records of 28 intact Holstein steers averaging 203.8 ± 37.5 kg live weight at the beginning of the experiment. These animals were kept in a rotational grazing system with feed supplementation. The analyzed data covers a period ranging from 420 to 635 days of age (14 to 21.1 months).

Location and management

The experiment was conducted at Los Dolores farm, in La Esperanza rural settlement located in Abejorral municipality (Antioquia, Colombia) from May to December of 2011. This municipality is located at 2,125 meters ASL, with 17° C average temperature, and 80% average relative humidity. Rainfall level is 2100 mm per year, and it is regarded as a tropical lower-montane wet forest (TLM-wf) (Holdridge, 1978).

Animals grazed on Kikuyu grass (Pennisetum clandestinum) pastures and were supplemented with reconstituted corn grain silage (RCGS) with water plus 2% urea (1 kg/day, dry base). This supplement was individually offered in a plastic container placed in the paddock. Nutritional composition of the diet is presented in table 1. Animals were offered water and mineralized salt (8% P) ad libitum. Paddock size and rotation periods were programmed to ensure a 45-d grazing interval and a 3-d maximum occupation period per paddock.

Animal health management followed the recommendations of the Colombian Agricultural Institute (ICA, 2007). Animals were weighed on a monthly basis since the beginning of the experiment, thus obtaining information from 14 to 21 months of age. Weighings were always taken at the same time, and no food was offered during the previous 12 hours.

This study was approved by the animal experimentation ethics committee of the Faculty of Agricultural Sciences at the University of Antioquia.

Statistical analysis

The growth functions evaluated are presented in table 2. Data fit for each model and parameter estimates were established using Marquardt's iterative algorithm of the PROC NLIN procedure for non-linear models available in the SAS software package (SAS, 2001).

Selection of the best model included the following criteria:

1. The sum of squared errors (SSE). The model with the lowest SSE best represents the data set (Noguera et al., 2008).

2. The Akaike information criterion (AIC; Akaike, 1973). This criterion weighs values among the maximum likelihood logarithm function using the residual variance and the number of parameters in the model.

3. The Bayesian Information Criterion (BIC; Schwarz, 1978). It is based on a probability integrated into the Bayesian theory.

4. The coefficient of determination (R2; Noguera et al., 2011).

The analysis of residuals was another criterion used to assess the fit of the models. Residuals were calculated as the difference between observed and predicted values. Table 3 shows how the calculations were performed for each criteria used to compare the models.

Additionally, genetic correlations were conducted between the model parameters with their level of significance through the PROC CORR procedure of the SAS software (SAS, 2001).

To verify compliance with the normality assumption of all residues from each model, the Shapiro-Wilk (SW) test was used through the PROC UNIVARIATE procedure of the SAS software (SAS, 2001).

The models were compared to determine their goodness of fit through analysis of variance of their evaluation criteria variance using the PROC GLM procedure of SAS (SAS, 2001), and the Tukey test for comparison of means. Differences were set at p<0.05. Total degrees of freedom were 83 (29 for the model and 54 for the error).

Results

Parameter estimates resulting from individually fitting non-linear growth models to weightage data of the animals are presented in table 4. Among the studied models, Brody reached the highest numerical estimated value for parameter A and Gompertz had the lowest value although no significant differences were found (p>0.05). Parameter K estimate by the Bertalanffy model was similar to that obtained by the Brody model; both values were lower than those obtained through the Gompertz model (p<0.05).

Table 5 shows values of the different quality fit criteria represented by SSE, R², AIC, and BIC for each of the studied models. The models with low SSE provided more accurate predictions of the phenomenon to be modeled. In this case, Bertalanffy showed a better fit than the other two models, however no significant difference was observed (p>0.05). The highest coefficient of determination (R²) was obtained with Gompertz (p<0.05), while Brody and Bertalanffy models had similar R² (p>0.05). This provides evidence that Gompertz is the most adjusted model.

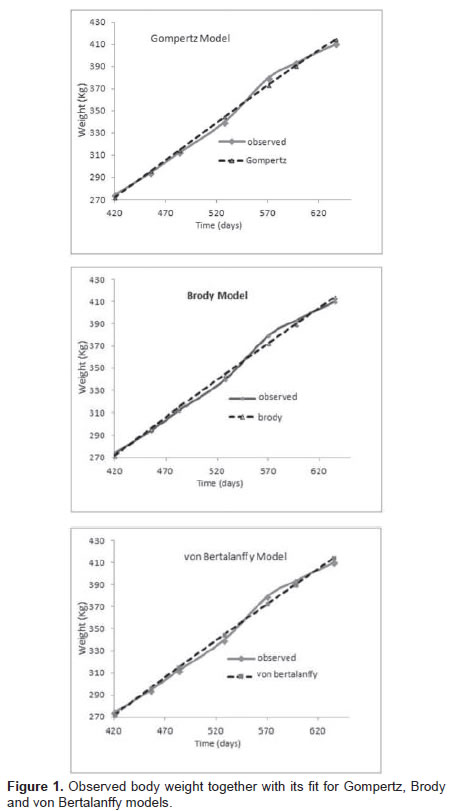
The AIC and BIC criteria can determine how well the models fit to a database; the best models are those having low estimation values. The values for the three models were equivalent (p>0.05), indicating that it makes no difference to choose any one. Visually, models presented very similar behavior regarding their ability to fit throughout the study (Figure 1). The difference between observed and predicted values was very similar among the evaluated models (Figure 2), indicating that animal weigth was similarly predicted by the models across time.

No individual model stood out by showing higher residual alternation (i.e., animal weight was both overestimated and underestimated throughout the studied age range).

Discussion

Mathematical models are based on assumptions to fit the data; this is evidenced by the difference in A, B, and K estimates (Table 4). Despite this, predicted values were very close to real values, which was confirmed by the criteria used to evaluate their goodness of fit.

According to Posada et al. (2011), total sum of squares (TSS) in different models is the same for a dataset, while Sum Squared Error (SSE) only depends on model fit. Likewise, models with low SSE fit better with only one dataset. According to this premise, the models studied in this work have similar goodness of fit used to describe the growth curve in intact Holstein steers within the period sampled.

The opposite happens with the coefficient of determination (R²); high values indicate greater goodness of fit. In this case, the highest value was observed with Gompertz, which was higher (p<0.05) than those of Brody and von Bertalanffy models (Table 5).

Growth curve was similar for all three models (Figure 1), fulfilling the assumption of normality of the residuals (Table 5), and obtaining a good fit of the models to the data (estimated growth curve). This condition of normality in the model residual ensures that the inference on the parameters was appropriate (Posada et al., 2011).

In this study, A, B, and K ranged from 795 to 1097.6, 0.236 to 12.403, and 0.0028 to 0.0047, respectively (Table 4). According to Silva et al. (2002) there is a genetic correlation between parameters A and K, indicating antagonism between the estimates for those parameters. Thus, this study confirmed that a negative correlation exists between mature weight (A) and maturity rate (K), as a negative correlation was found (r) for all three models. The values were r = -0.56 (p = 0.002) for von Bertalanffy, r = -0.56 (p = 0.0019) for Brody, and r = -0.44 (p = 0.019) between these parameters.

Several authors have referred to the close and negative correlation between those parameters, reporting—for instance—values of r = -0.736 (Kratochvílová, et al., 2002), r = -0.69 (Marshall, et al., 1984) and r = -0.57 (DeNise and Brinks, 1985). Genetic correlation between A and K is antagonistic between the estimates of those parameters. Therefore, when selecting animals with a high maturity rate, animals tended to achieve lower adult weight. However, Holstein breeding programs aim to achieve both. This indicates that both a large body structure and precocity must be simultaneously present (Kratochvílová et al., 2002). The values reported by Kratochvílová et al. (2002) for Holstein cattle were A = 643.45 and K = 0.00367. These were low for A and intermediate for K when compared with values in our study. Similarly, upon comparison with Zebu cattle, values found in the same models were low for A (Brody: 923.5; Gompertz: 640.5; and von Bertalanffy: 689.8) and high for K (Brody: 0.0010; Gompertz: 0.0028; and von Bertalanffy: 0.0022) as in the study conducted by Posada et al. (2011).

In this study, values for A were high and values for K were low. This indicates that animals will reach asymptotic weight at an older age based on a slower development. This is consistent with reports by Herrera et al. (2008) who claim that animals with high asymptotic weights (A) are less premature, as they have low values for growth rate (K). Additionaly, prediction of asymptotic weight through growth curves can be affected by the type of environment and food during breeding, fattening, and rearing (Arango and Van Vleck, 2002).

The value for A found in this study with Gompertz model is 13 kg higher than that reported by Herrera et al. (2008) for Holstein X Zebu steers and other Zebu crosses weighing 520 kg. This, paired with increased growth rate (K), indicates less precocity for pure Holstein steers. The integration constant (B), has no biological significance in the model; data found in this study was 12 points higher than that reported by Herrera et al. (2008).

Comparing asymptotic weight (A) in this study with that reported by Brown et al. (1972) who worked with Angus and Herford steers, Holstein outweighed Angus and Hereford by 3 and 84 kg, respectively, while growth rates of Angus and Hereford were greater than those of Holstein, indicating greater precocity in Holstein. This can be understood with the assertions by Brown et al. (1972) who concluded that animals with different values of A may have similar or different values of K. Only when two animals are growing with similar mature weights can K be interpreted as a measure of the differences in growth rate. Otherwise K measures differences in growth rate compared to asymptotic weight. Furthermore, different growth patterns are achieved when two mature animals have similar weights but different K values, or similar K values but different mature weights. Additionally, different mature weights and different K values may or may not represent different growth patterns.

On the other hand, the Gompertz model had the greatest goodness of fit to the data in this study because, besides having a good mathematical fit (R², SSE, AIC, BIC), it also shows suitable biological consistency in the estimated mature weight and is consistent with the value obtained by Kratochvílová et al. (2002), which was 643.35 kg for Holstein steers. Similarly, if we take into account the marketing and processing weights of Holstein steers in the U.S. reported by Siemens (1996) —ranging from 535 to 636 kg—, Forni et al. (2006) mentioned that these alternative models are valid for predicting adult weight, considering that adult weight comes after profit and is a valuable contribution to beef cattle genetic improvement programs.

Regarding the available mathematical models, Gompertz is not the most commonly used model for describing growth curves in steers, but rather the model proposed by Brody. However, in this case Gompertz showed better goodness of fit for the coefficient of determination (p<0.05) than Brody's model. Furthermore, these results agree with those reported by Silva et al. (2002) who concluded that Brody's function overestimates asymptotic weight and the Gompertz function has the highest percentage of convergence. Furthermore, Bergamasco et al. (2001) found that Brody overestimates asymptotic weight in female Holstein cattle. Likewise, Silva et al. (2002) stated that Brody's model is most suitable when a small number of weighings is available, which is the case in our study.

According to these results, it can be stated that the Gompertz model was the best at describing growth of intact Holstein steers under rotational grazing with supplementation.

Notas

Acknowledgements

Authors would like to thank the Colombian Ministry of Agriculture and Rural Development and the Sustainability Project 2011-2012 (Estrategia de sostenibilidad CODI, University of Antioquia) for providing the resources for the study. We also wish to thank FRIGOCOLANTA for allowing us to use its facilities, and to Velásquez-Duque family in Abejorral municipality for assistance with data collection.

References

Akaike H. Information theory and an extension of the maximum likelihood principle. In: B.N. Petrov and F.Csaki, editors. 2nd International Symposium on Information Theory 1973:267-281.         [ Links ]

Arango JA, Van Vleck LD. Size of beef cows: early ideas, new developments. Genet Mol Res 2002; 1:51-63.         [ Links ]

Bergamasco AF, Aquino LH, Muniz JA. Estudo da curva de crescimento de fêmeas da raça Holandesa. Ciênc Agrotec 2001; 25:235-242.         [ Links ]

Brown JE, Brown CJ, Butts WT. A discussion of the genetic aspect of weight, mature weight and rate of maturing in Hereford and Angus cattle. J Anim Sci 1972; 34 4:525-537.         [ Links ]

Brody S. Bioenergetics and growth. New YorK: Reinhold Publishing Corp; 1945.         [ Links ]

Brown JE, Fitzhugh HA, Cartwright TC. A comparison of nonlinear models for describing weight-age relationships in cattle. J Anim Sci 1976; 42:810-818.         [ Links ]

DeNise SK, Brinks JS. Genetic and environmental aspects of the growth curve parameters in beef cows. J Anim Sci 1985; 61:1431-1440.         [ Links ]

Forni S, Piles M, Blasco A, Varona L, Oliveira HN, Lôbo RB, Albuquerque LG. Genetic analysis of growth curve parameters applying a von Bertalanffy function to beef cattle longitudinal data. 8th World Congress on Genetics Applied to Livestock Production, Belo Horizonte, MG, Brasil 2006; p. 3-16.         [ Links ]

Herrera AC, Vergara OD, Cerón-Muñoz MF, Agudelo DA, Arboleda EM. Curvas de crecimiento en bovinos cruzados utilizando el modelo Brody. Livest Res Rural Dev 2008; 20:140        [ Links ]

Holdridge L. Ecología basada en zonas de vida. San José:IICA;1978.         [ Links ]

ICA, Instituto Colombiano Agropecuario. Resolución No 002341 de 23 de agosto 2007.         [ Links ]

Kratochvílová M, Hyánková L, Knížetová H, Fiedler J, Urban F. Growth curve analysis in cattle from early maturity and mature body size viewpoints. Czech J Anim Sci 2002; 47 4:125- 132.         [ Links ]

Marshall TE, Mohler MA, Stewart TS. Relationship of lifetime productivity with mature weight and maturation rate in Red Poll cows. Anim Prod 1984; 39:383-387.         [ Links ]

Nobre PR, Rosa A, Silva LO, Evangelista SR. Curvas de crescimento de gado Nelore ajustadas para diferentes freqüências de pesagens. Pesq agropec bras 1987; 22:1027- 1037.         [ Links ]

Noguera RR, Pereira RL, Solarte SE. Comparación de modelos no lineales para describir curvas de crecimiento en cuyes (Cavia porcellus) desde el nacimiento hasta la edad de sacrificio. Livest Res Rural Dev 2008; 20:5.         [ Links ]

Noguera RR, Ortiz DR, Marin LS. Comparación de modelos matemáticos para describir curvas de lactancia en cabras Sannen y Alpina. Livest Res Rural Dev 2011; 23:11.         [ Links ]

Posada S, Rosero R, Rodríguez N, Costa A. Estimación de parámetros de curvas de crecimiento de ganado Nellore criado en confinamiento. Rev MVZ Córdoba 2011; 16:2701-2710.         [ Links ]

SAS/STAT. Guide for Personal Computer. Versión 8.2. Cary (NC): SAS Institute Incorporation; 2001.         [ Links ]

Siemens M. Managing Holstein steers for beef production. US department of agriculture, University of Wisconsin. [access date: January 9, 2012]. URL: http://learningstore.uwex.edu/assets/pdfs/A3659.pdf 1996.         [ Links ]

Souza JC, Bianchini SE. Estimativa do peso de bovinos de corte, aos 24 meses, da raça Nelore, usando curvas de crescimento. Rev Bras Zootecn 1994; 23:85-91.         [ Links ]

Schwarz G. Estimating the dimension of a model. Annals of statistics 6 1978;461-464.         [ Links ]

Silva FF, Aquino LH, Oliveira AI. Estimativas de parâmetros genéticos de curva de crescimento de gado nelore (Bos indicus). Ciênc Agrotec 2002; 34:1562-1567.         [ Links ]

von Bertalanffy L. Quantitative laws in metabolism and growth. The quarterly review of biology 1957; 32:217-231.         [ Links ]

Winsor CP. The Gompertz curve as a growth curve. Proc Natl Acad Sci 1932; 18:1-7.         [ Links ]