Introduction

Reproductive performance is the most important component of production efficiency in beef production systems. However, reproductive traits in cattle are difficult to measure, report and interpret. This is particularly true for pasture mating situations, where information on females is extremely limited. In these situations, the only information readily available is whether or not a cow produces a calf, and when it calves (^{Cammack et al., 2009}; ^{Yagüe et al., 2009}). A delay in conception due to poor fertility prolongs the calving interval and causes a shift in the calving pattern, which can lead to culling. Calving interval -the period between calving and conception- directly influences the profitability of beef cattle systems since it determines the number of calves born. Calving interval also impacts the generation interval, which limits the intensity of selection. Calving interval includes both days open and gestation length. Ideally, days open varies between two and three months, allowing for uterine involution and return of ovarian activity and production of one calf annually. Gestation length is also an important trait because animals with longer gestations must have fewer days open in order to maintain a 365 day calving interval. Thus, decreases in both traits can improve reproductive efficiency of cattle herds (^{Azevêdo et al., 2006}).

The Nellore breed is the mainstay of the beef industry in Brazil. Nellore cows are well adapted to tropical conditions, have good maternal ability, low incidence of dystocia and a long and prolific reproductive life. However, like other Bos indicus breeds, Nellore cattle tend to reach puberty later than Bos taurus breeds (^{Sanders, 1980}). There is a great variability for age at first calving in Nellore cattle (Gunski et al., 2001), which indicates the possibility of genetic selection to reduce this age. Therefore, this research was carried out to estimate and analyze the genetic parameters for reproductive traits of Polled Nellore cows in order to inform selection programs and to improve herd reproductive efficiency of the breed.

Material and methods

Data were obtained from OB Group herds, located in Midwestern Brazil, in Pontes e Lacerda, Mato Grosso, a region with transitional vegetation between the Cerrado biome and the Amazon rainforest. It is a region of humid tropical climate, with an average altitude of 254 meters above sea level and average annual precipitation of 1,500 mm.

The traits analyzed included: age at first calving (AFC), calving interval (CI), gestation length (GL) and days open (DO). Data on reproductive performance were collected from 1977 to 2009. Data were edited for consistency of pedigree information and correct dates of birth, calving and weighing. Records with anomalies in pedigree information and dates were discarded. Also discarded were records of animals with AFC greater than 2,200 days, CI less than 300 and greater than 750 days, DO less than 40 and greater than 280 days and GL less than 260 and greater than 310 days. After data editing, the dataset was composed of 9,663, 28,785, 24,529, and 27,944 records of AFC, CI, DO, and GL, respectively. The pedigree, data structure, and summary statistics for each trait are presented in Table 1.

Table 1 Description of the final data set and statistical summary for reproductive traits in Polled Nellore cows. 

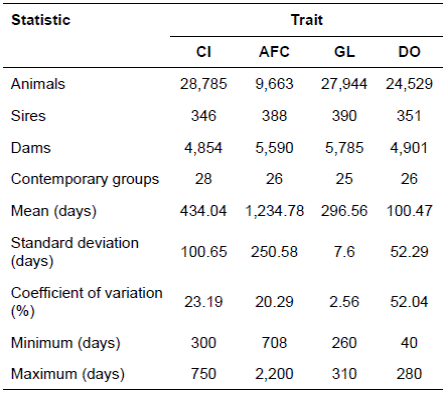
CI: calving interval; AFC: age at first calving; GL: gestation length; DO: days open.

Genetic analyses were carried out fitting a model that included the following effects: age of the cow as covariate; sex of the calf coded at two levels (male or female); season of birth, calving season, and mating season all coded at four levels (from January 1 to March 31, from April 1 to June 30, from July 1 to September 30, and from October 1 to December), calving year, birth, and mating years, and herd.

Fixed effects included in the model were: for AFC, herd-year-season of birth of cow and sex of the calf; for CI and DO, herd-yearseason of calving and sex of the calf; and for GL, herd-year-season of mating and sex of the calf. To define the fixed effects included in the contemporary group (CG), statistical analyses were performed using the least-squares method, and stepwise regression, through the GLM and REG procedures, respectively -SAS 9.2 program (SAS Institute Inc., Cary, NC, 2004)-. The CG with fewer than three records and sires with fewer than three offspring were also removed from the final data file.

The animal model used for AFC and CI included CG and mating method (natural service or artificial insemination), age of cow as a covariate (linear and quadratic effects), and random effects of animal and residual. For CI, DO, and GL, the models included random animal, permanent environmental effects and residual. For GL, the model also included CG and mating method. For DO, the model also included CG and age of cow as covariate (linear and quadratic effect).

The analyses were conducted by fitting single and two-trait animal models. In matrix notation the mixed linear models for AFC (1) and CI, GL and DO (2) were:

() 1

() 2

Where:

β = is the fixed effects vector associated with the observation (records) vector y by the known matrix X and a.

pe = are the random effects vector (additive genetic and permanent environmental effects) associated with records in y by the incidence matrix Z ₁ and Z ₂.

e = is the residuals vector.

Covariance components and genetic parameters for the four analyzed traits were estimated via a Bayesian procedure using MTGSAM software (Multiple Trait using Gibbs Sampler under Animal Model; ^{Van Tassell and Van Vleck, 1996}). The prior distributions of the additive values (a), the permanent environmental effects (pe) and the residual effects (e) were:

Where:

A = is the additive relationship matrix.

I = is the identity matrix.

are the genetic additive, permanent environmental and residual variances, respectively.

It is also assumed that both the systematic effects listed above and the (co)variance components included in the fitted model have a uniform Gaussian a priori distribution, whilst the conditional distributions of the additive, permanent environmental and residual variances have an inverse Wishart distribution (^{Sorensen and Gianola, 2002}).

The marginal posterior distribution for each parameter is obtained via integration of multivariate density functions using a Gibbs sampling procedure, with a period of data collection for multi-trait analyses of 1,500,000 interations, a burn-in period of 500,000 interations, of 2,500,000 interations, and a burn-in period of 500,000 interations for single-trait analyses. The final file was composed of samples collected every 1,000 and 2,000 interactions for multi- and single-trait analyses. The estimates for each parameter included in the model were given with the corresponding Bayesian interval, defined by the 95% highest posterior density (HPD95).

Breeding values were calculated utilizing all pedigree information available. Genetic trends were computed as a linear regression of average predicted breeding values for the traits versus the dam’s birth year using the REG procedure (SAS, 2004), according to ^{Filho et al. (2005}).

Results

Means for AFC, CI, GL, and DO were 1,234.78 ± 250.58, 434.04 ± 100.65, 296.56 ± 7.6, and 100.47 ± 52.29 days, respectively. The posterior variances, standard deviations and credibility intervals along with the means, medians of the variance components and heritabilities for the single-trait models of the female traits are shown in Table 2. The mean and median for the reproductive trait variance components were similar to each other. The measures of central tendency of genetic parameter values were identical, indicating that these posterior marginal distributions tended to symmetry.

Table 2 Estimates of the means, standard-deviations, medians and bounds of highest posterior density intervals at 95% (HPD95) of the marginal posterior distributions of (co)variance components and genetic parameters for age at first calving (AFC), calving interval (CI), gestation length (GL), and days open DO). 

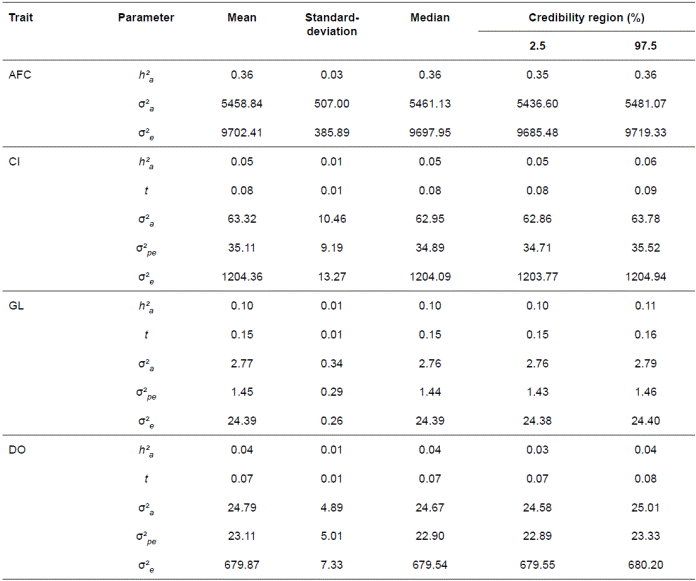
σ²a: Genetic additive variance; σ²pe: permanent environmental variance; σ²e: Residual variance; h²a: genetic additive heritability; t: repeatability

Three of the four traits showed low but statistically significant heritabilities, with averages of 0.05, 0.10, and 0.04 for CI, GL, and DO, respectively, whereas AFC had a higher heritability of 0.36. The permanent environmental components associated with CI, GL, and DO were also low, averaging 0.08, 0.07, and 0.15, respectively. All the estimates of heritability and repeatability showed narrow HPD95 bounds.

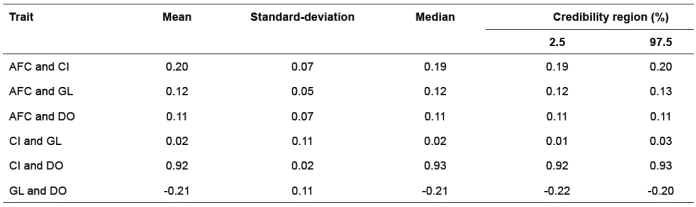
Estimates of posterior density and traces of heritability estimates for AFC, CI, GL, and DO are shown in Figure 1, and repeatability estimates are shown in Figure 2. Table 3 gives the estimates of the mean, standard deviation, median and bounds of HPD95 of the marginal posterior distribution of genetic correlations between each pair of traits analyzed.

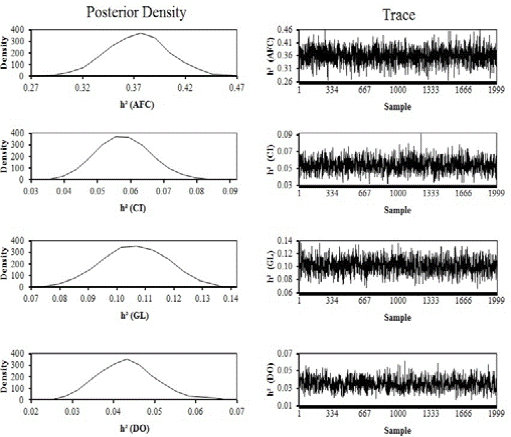
Figure 1 Estimates of posterior density and traces of heritability estimates (h²) for age at first calving (AFC), calving interval (CI), gestation length (GL), and days open (DO) by single-trait analyses. 

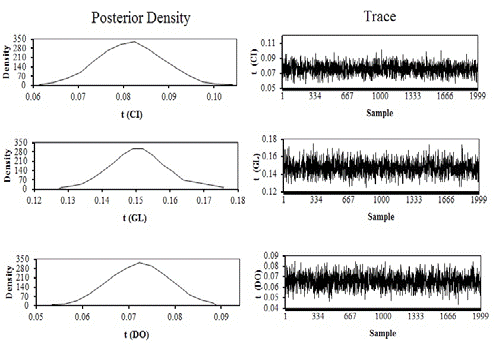
Figure 2 Estimates of posterior densities and traces of repeatability estimates (t) for calving interval (CI), gestation length (GL) ,and days open (DO) by single-trait analyses. 

Table 3 Estimates of the means, standard-deviations, medians, modes and bounds of highest posterior density intervals at 95% (HPD95 in brackets) of the marginal posterior distributions of genetic correlation for age at first calving (AFC), calving interval (CI), gestation length (GL), and days open (DO). 

Estimate of posterior density and traces of genetic correlation between AFC and CI, AFC, and GL, AFC and DO, CI and GL, CI and DO, and GL and DO are shown in Figure 3.

Annual (birth year) direct genetic trends of breeding value of dam for AFC, CI, GL, and DO over 32 years are shown in Figure 4. Genetic trends for all traits were highly significant (p<0.0001) and showed coefficients of determination for AFC, CI, GL, and DO of 0.42, 0.21, 0.28, and 0.20, respectively.

Figure 3 Estimates of posterior densities and traces of genetic correlation estimates (ra) between age at first calving and calving interval (AFC x CI), age at first calving and gestation length (AFC x GL), age at first calving and days open (AFC x DO), calving interval and gestation length (CI x GL), calving interval and days open (CI x DO), and gestation length and days open (GL x DO). 

Figure 4 Genetic trends (days) for age at first calving (AFC), calving interval (CI), gestation length (GL), and days open (DO). 

Discussion

With the use of multiple-trait analyses, estimates of correlations between traits can be obtained, which is not possible with singletrait analyses. The samples obtained for the genetic correlations did not show wide dispersion, i.e. the oscillations remained stable, thus indicating that the burn-in period used in the analyses was adequate and allowed convergence of the chain (^{Gelfand and Smith, 1990}).

Although the value for DO was above the ideal (60-90 d) for producing a calf/cow/year, particularly considering the long gestations, the genetic variability for this trait indicates the possibility of reducing this period. These results are in accordance with a previous report (^{Azevêdo et al., 2006}) that DO and GL averaged 165.76 ± 110.29 d and 295.03 ± 5.85 d, respectively. Therefore, the joint assessment of traits such as AFC, CI, GL, and DO are essential for the success of the selection process.

Age at first calving is routinely recorded and was genetically correlated with calving interval and has been often used to evaluate heifer fertility. Calving interval is the number of days between successive calvings and is also an easily measurable trait used as an indicator of female fertility. Although this measure has been a principal measure of reproductive health throughout the productive life of the cow, it may not be the most appropriate measure of overall reproductive ability. Some authors (^{Cammack et al., 2009}; ^{Gutiérrez et al., 2002}) have reported that later age at first calving is associated with a decrease in lifetime productivity of the beef female. Therefore, due to the positively genetic correlation between AFC and CI, and the moderate heritability (0.36) for AFC, it should be possible to decrease both traits by selecting for lower AFC.

The low heritabilities for CI, GL, and DO were associated with high environmental variance. This suggests that these traits were heavily influenced by the extensive nutritional conditions, management, and tropical climate, and that genetic improvement for this trait would be slow. If nutrition and management of the cow-calf herd and replacement heifers were improved, this may permit fuller expression of genetic potential and possibly faster genetic progress for CI, GL, and DO in this population.

On the other hand, the 0.36 heritability estimate for AFC indicates that selection for this trait would likely result in a decrease in AFC over time. Other studies have also reported high variability in heritability estimates for this trait in Nellore cattle, i.e. 0.14,0.09, 0.11, 0.26, 0.15 (^{Boligon et al., 2007}; ^{Faria et al., 2007}; Boligon et al., 2008; ^{Pereira et al., 2001}; ^{Laureano et al., 2011}; respectively). Our results indicate that age at first calving presents moderate heritability and is recommended as a selection criterion for sexual precocity. However, nutritional and reproductive management must also be adequate to obtain satisfactory responses.

The low heritability estimates for CI, GL, and DO indicate that significant improvement through selection will be attainable only through enhanced accuracy of selection by, for example, incorporating information on correlated traits (Makgahlela et al., 2008). The genetic correlation between DO and CI was 0.92, while genetic correlations between DO and the other reproductive traits were low to negative (0.11 for AFC and -0.21 for GL, respectively).

The average breeding values for AFC, CI, GL, and DO were 2.082, 0.071, 0.019, and -0.049 kg, respectively, all highly significant (p<0.0001), which means that at least age at first calving, calving interval and days open have been used as selection criteria in this herd, and some improvement has been achieved on these traits. Over 32 years, AFC, CI, and DO decreased from 5.24 to 1.08 days, 15.03 to -58.01 days and 4.89 to -0.32 days per year, respectively. By contrast, gestation length increased from -1.52 to 0.26 days per year. Genetic trends were irregular for all traits -some years positive and some years negative. The trend for GL showed that there has been no selection for decreasing gestation length in this herd. This could be due to the fact that selection was mainly focused on production traits.

The decreasing trend observed for AFC and CI indicates an improvement in the genetic merit for these traits (Makgahlela et al., 2008; ^{Gunawan et al., 2011a}). Gunawan et al. (2011b) considered that this might be partly a correlated response to selection for increased daily gain. A possible cause of the undesirable trend in gestation length and of the marked fluctuation of values observed for AFC, CI, and DO could be the intense selection to increase productive traits (^{Lopes et al., 2011}; ^{Santos et al., 2012}; Lopes et al., 2013), without giving attention to reproductive traits.

Selection for fewer days open would contribute towards shorter calving intervals because the genes that act on one trait also act on the other. However, selection for decreased gestation length could result in a greater number of days open due to the antagonism between these traits. Despite the favorable genetic correlations between age at first calving and calving interval, gestation length, and days open, respectively, and between calving interval and gestation length, the selection response for these traits would be low due to low heritabilities caused by the strong environmental influence on these variables. Overall, genetic trends for age at first calving, calving interval and days open decreased from 1977 to 2009. However, gestation length increased over the same period. Changes in management and environmental factors could rapidly improve reproductive performance of Polled Nellore herds. Genetic selection for these traits should produce a much slower but permanent response.

Acknowledgements

The authors thank the OB Ranch for kindly providing records and to ANCP (Brazilian Society of Breeders and Researchers) for providing pedigree data.

Conflicts of interest

The authors declare they have no conflicts of interest with regard to the work presented in this report.

Notes

To cite this article: Ulhôa C, Brito F, de Malgalhaes GJ, Sainz RD. Bayesian estimates of genetic parameters for reproductive traits in Nellore cows raised on pasture in tropical regions. Rev Colomb Cienc Pecu 2016; 29:119-129