ESTIMACIÓN DEL VOLUMEN DE MADERA EN ÁRBOLES MEDIANTE POLINOMIO ÚNICO DE AHUSAMIENTO

Estimating the volume of the wood of trees through the unique taper polynomial

Orlando Riaño Melo¹ & Iván Lizarazo²

¹ Universidad Distrital Francisco José de Caldas. Bogotá, Colombia. orianom@unal.edu.co Autor para correspondencia.
² Universidad Nacional de Colombia. Bogotá, Colombia. ializarazos@unal.edu.co

Riaño M, O. & Lizarazo, I. (2017). Estimación del volumen de madera en árboles mediante polinomio único de ahusamiento.Colombia Forestal, 20(1), 55-62.

Recepción: 2 de abril de 2016 / Aprobación: 24 de octubre de 2016

RESUMEN

La estimación del volumen de madera de los árboles es una tarea costosa, dispendiosa y difícil de llevar a cabo de manera confiable. Los métodos tradicionales de cubicación de madera ajustan modelos matemáticos preexistentes para especies y áreas específicas, los cuales tienen alto costo operativo y ecológico pues se debe apear un número importante de los árboles en pie. Este artículo presenta un modelo alternativo de cubicación individualizada, que utiliza un único polinomio que no obliga a derribar el árbol, es relativamente rápido y económico, permite cuantificar el volumen del árbol con buena exactitud y puede extenderse para estimar el volumen comercial de la plantación o rodal. Para ello se presenta matemáticamente el método propuesto, se utiliza para estimar el volumen de un árbol muestra y se compara su resultado con los obtenidos por cinco métodos que se emplean en la cubicación del árbol presentados por la FAO (1980). Los resultados muestran que el polinomio único presenta un error relativo máximo que no supera el 1.6 % en ningún caso y permite obtener, de manera sencilla, el diámetro a una altura dada y la altura para un determinado diámetro.

Palabras clave: función de ahusamiento, perfil, volumen.

ABSTRACT

Estimating the volume of wood from trees is an expensive, time-consuming and error-prone task. Traditional methods use mathematical models that need to be matched to existing species and specific areas using a case by case approach. Such methods have high operating and environmental cost, as several trees in the plantation are cut down. This article presents an alternative model to quantify the volume of a tree, which uses a single polynomial, which requires not felling the tree, which is relatively quick and inexpensive with good accuracy, and can be extended to estimate the trade volume of the plantation. To this end, the proposed method is described mathematically and its results compared with those obtained for five ideal methods described by FAO (1980). Results show that the polynomial method has a maximum relative error that does not exceed 1.6 % in any case and allows calculating tree’s diameter at a given height and height for a given diameter.

Keywords: taper function, profile, volume.

INTRODUCCIÓN

Un problema recurrente que afrontan los encargados del proceso de planificación forestal es la estimación confiable del volumen de madera de los árboles y de los rodales, así como lo que producirá el bosque en diferentes sitios con distintos tratamientos silvícolas (FAO, 1980; Corral et al., 1999; García et al., 2009; López et al., 2015). Esta tarea resulta costosa (Kleinn, 2000), toma mucho tiempo (Cancino, 2006), es dispendiosa y difícil de llevarla a cabo de manera precisa, salvo que se usen escaleras forestales o se apeen los individuos (Mancera, 2014).

Las dificultades señaladas han llevado a que los ingenieros forestales realicen la cubicación de los volúmenes de árboles ajustando modelos matemáticos preexistentes, los cuales permiten estimar el volumen comercial en función de variables obtenidas mediante mediciones simples de una muestra de árboles, como su altura, forma y diámetro a la altura del pecho (Prodan et al., 1997; Cancino, 2006; Galán et al., 2008).

El ajuste matemático de estos modelos para especies y áreas específicas es una tarea que tiene alto costo operativo y ecológico (García, 1995), dado que se debe apear una muestra representativa de las diferentes clases diamétricas de los árboles existentes en pie (Cuevas, 2008) para obtener un modelo particular que permita calcular el volumen con exactitud, lo cual constituye usualmente un procedimiento lento y costoso (García, 1995).

A través del tiempo, se han desarrollado ecuaciones para simular el ahusamiento de los árboles, desde los más simples (Kozak et al., 1969; Demaerschalk, 1972; Ormerod, 1973; Hilt, 1980) hasta polinomiales segmentados (Bruce et al., 1968; Max & Burkhart, 1976; Cao et al., 1980; Parresol et al., 1987), incluso geométricos y trigonométricos (Parresol & Tomas, 1996; Fang & Bailey, 1999; Bi, 2000; Zhang et al., 2002), modelos de exponente o forma variable y modelos de interpolación numérica como el Spline cúbica (Zapata, 2011). A pesar de estos aportes, se carece de un modelo que explique adecuadamente la variación de la forma del fuste (Newnham, 1998).

Este artículo presenta un modelo alternativo de cubicación individualizada que no obliga a derribar el árbol (se emplea un dendrómetro láser), es relativamente rápido, económico y exacto (referido a que tan cerca llega una medida u observación a la medición del valor verdadero), que permite cuantificar el volumen del árbol y que puede extenderse para estimar el volumen comercial de una plantación o rodal. Para el efecto, se describe matemáticamente el método propuesto y se comparan sus resultados con los obtenidos por Cailliez (FAO, 1980), empleando cinco métodos para la cubicación de árboles.

METODOLOGÍA

En este estudio se toma, a manera de ejemplo, los datos de un árbol apeado (FAO, 1980) en el cual se han medido los diámetros con intervalos de un metro, empezando en el tocón (a 20 cm del suelo) y el diámetro a la altura del pecho (dap). En la tabla 1 se muestran cinco métodos diferentes de cálculo del volumen total del fuste, empleando diferentes trozas. Como los cinco métodos producen resultados muy similares, no es posible establecer cuál de ellos está más cercano a la realidad a menos que se utilice el método por desplazamiento de líquido de un recipiente (xilómetro) (FAO, 1980).

Teniendo en cuenta que las diferentes partes del fuste de un árbol no presentan formas geométricas bien definidas tales como cilindros, conos, paraboloides o neiloides, los métodos tradicionales se basan en el principio de medir el diámetro a diferentes alturas y calculan el volumen del árbol a partir de dichas mediciones. Se asume que el fuste a cualquier altura posee una circunferencia exacta (Zapata, 2011; Campos & Leite, 2013). En las expresiones empleadas a continuación representan las circunferencias de cada extremo y de la parte central de la troza respectivamente (figura 1) y 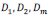 son los diámetros de las circunferencias  respectivamente. Las fórmulas usadas en las estimaciones del volumen del árbol de la tabla 1 son las clásicas:

Fórmula de Huber: toma su nombre a partir de 1837. Es la más sencilla de emplear, solo requiere determinar la circunferencia de la sección media C_m y su longitud. El volumen se estima así:

Fórmula de Smalian: aparece en 1806. Se deben evaluar las áreas de las secciones extremas C₁ y C₂ y su longitud. El volumen se valora mediante la expresión:

Fórmula de Huber modificada: se utiliza cuando se hace difícil o imposible determinar el diámetro de la circunferencia media. Por ello, se miden los diámetros o radios de las secciones extremas C₁ y C₂ y se obtiene su media aritmética para estimar el volumen con la fórmula:

Fórmula del cono truncado: la expresión para estimar el volumen viene dada por:

Fórmula de Newton: Riecke (1940) generaliza la fórmula propuesta por Then. Se aplica a un mayor número de cuerpos geométricos. Para la estimación del volumen se emplea:

El método alternativo que se propone en este estudio consiste en medir con un dendrómetro láser la docena de puntos: (0, d_o/2), (h/10, d₁/2), (2h/10, d₂/2), (3h/10, d₃/2), … (9h/10, d₉/2), (h, d₁₀/2), (1.3, dap/2). En los que h es la altura total del árbol, d_i es el diámetro a una altura ih/10 y dap es el diámetro a la altura del pecho, y así obtener una ecuación polinómica, P(X) que pase por todos ellos. Debido al ahusamiento del fuste o coeficiente de decrecimiento del diámetro en relación al incremento de la altura total del árbol se tiene que: d₀>d₁>…>d₉>d₁₀ (figura 2). En consecuencia, el polinomio de interés está dado por:

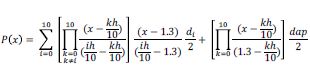
que cumple:

para todo i= 0, 1, 2, …, 10, y , lo que significa que el perfil así definido pasa por cada una de las 12 mediciones realizadas al árbol.

Para estimar el volumen del fuste se rota P(x) sobre su eje en el intervalo [0, h], con lo que se obtiene:

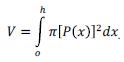
Integral que se calcula numéricamente con ayuda de algún programa de álgebra computacional como Derive^®, Maxima^® o Scientific Workplace^®.

RESULTADOS

Al aplicar la expresión presentada del polinomio único usando los datos de la tabla 1, para la altura total h = 9.3 m y las parejas ordenadas de altura (m), diámetro (cm): (0, 35), (1, 32), (1.3, 30.34), (2, 28), (3, 20), (4, 17), (5, 13), (6, 10), (7, 8), (8, 4.52), (9, 1.14) y (9.3, 0), el perfil del fuste queda descrito por el polinomio:

y el volumen del fuste es:

que por integración numérica produce:

V = 0.2688 m³.

Los valores estimados resultantes del volumen por los seis métodos se muestran en la tabla 2

DISCUSIÓN

Para confrontar el resultado obtenido por el método del polinomio único con los resultados de cada uno de los cinco métodos tradicionales de trozado indicados en la tabla 1 se calcula el error relativo desde dos perspectivas diferentes:

· Tomando los valores de volumen de cada uno de los cinco métodos tradicionales como el valor exacto V y el valor del volumen del polinomio único como aproximación .

· Asumiendo el valor del volumen del polinomio como valor exacto y los valores de volumen de cada uno de los métodos tradicionales como aproximación.

La tabla 3 muestra el error relativo con cada una de las perspectivas indicadas.

Se observa que con el método 4 en ambos casos se obtienen los valores de mayor error relativo y que no superan el 1.6 %, lo que muestra que la exactitud en la estimación del volumen depende en gran parte de las mediciones de los diámetros y no tanto del cálculo empleado. Con el método 1, que aplica la clásica formula de Smalian y del cono, el error relativo en ningún caso supera el 1 %. Los errores obtenidos con el método 2, que emplea la fórmula de Huber modificada y del cono, muestra el menor valor en ambas perspectivas, resultado similar al reportado en la literatura (Biging, 1988; Figueiredo & Budant, 1999).

Con este polinomio P(x)se tiene, con muy buena exactitud, que este pasa por cada uno de los puntos. Esto es que: 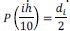para todo i= 0, 1, 2, …, 10, y . Por ejemplo:

cuyos valores coinciden con las medidas de los diámetros iniciales. Además, puede evaluarse P(x) para todo 0 ≤ x ≤ 9.3, mientras que con ninguno de los cinco métodos mostrados en la tabla1 puede realizarse en todo este dominio directamente.

Con la expresión P(x) puede encontrarse la altura correspondiente para cualquier diámetro que se requiera con fines de cortes para volumen total (desde la base del árbol hasta el ápice), volumen comercial (desde la base a un diámetro mínimo establecido, normalmente 10 cm), volumen aserrable (desde el tocón hasta 25 cm de diámetro mínimo), volumen de pulpa (entre 25 y 10 cm de diámetros límites) como lo sugieren García (1995) y Campos & Leite (2013). Por ejemplo, si desea establecer la altura correspondiente, para aprovechamiento forestal, donde el diámetro sea de 12 cm, deberá resolverse la ecuación:

P(x)=0.06

que se satisface para x=5.23 Y si es para volumen aserrable, la altura se calcula resolviendo para el diámetro de 25 cm:

P(x)=0.125

que indica cortar a x=2.35. Estas dos últimas características que presenta el polinomio único de ahusamiento P(x), muestran una gran ventaja sobre cualquiera de los cinco métodos presentados en la tabla 1, en los que con ninguno de ellos podrían responderse con mayor exactitud el anterior par de planteamientos.

Se puede establecer que en el método polinomial propuesto se modela el ahusamiento de los árboles con una sola ecuación que mediante su integración permite estimar el volumen del árbol.

La expresión propuesta podrá aplicarse siempre y cuando no se tengan diámetros iguales a diferentes alturas, pues se anularía el denominador.

El polinomio único de ahusamiento puede obtenerse para cualquier individuo del cual se tengan las medidas de sus diámetros a diferentes alturas y no necesariamente a décimos ni regularmente espaciadas.

CONCLUSIONES

A partir de la función de ahusamiento propuesta es posible estimar directamente el diámetro a cualquier altura de la fusta. Por transformaciones algebraicas a la ecuación también se estima el volumen total o volumen de cualquier sección del fuste, además de la altura total o comercial hasta un diámetro definido.

La ecuación con la que se estima el volumen de la madera del árbol muestra una mejora de los métodos tradicionales de evaluarlo mediante trozas.

No es tan trascendental determinar que método es el mejor para el cálculo del volumen porque la exactitud en la estimación depende más de las mediciones del diámetro que del cálculo empleado en sí, pero para poder establecer las alturas correspondientes a diámetros determinados o evaluar los diámetros a ciertas alturas, el método polinomial muestra su bondad al tener que resolver una simple ecuación.

Este estudio muestra que se puede determinar el volumen del fuste a partir de una sola ecuación polinómica simple con variables de fácil medición, empleando los dendrómetros láser que se encuentran en el mercado.

La mayoría de los modelos de ahusamiento reportados en la literatura suponen que los perfiles de los árboles siguen formas simples, como conos neiloides o paraboloides, lo que en la realidad no es fácil de identificar en el terreno dado que no existen reglas claras sobre cómo realizar esa asignación de formas.

La función polinómica presentada satisface las deseables propiedades: el diámetro es cero en el ápice y que a una altura de 1.30 m su diámetro es el dap. Mientras que los modelos segmentados pueden no cumplir la estimación del diámetro cero en el ápice y no proporcionar el dap a la altura de 1.3 m.

Es conveniente realizar una evaluación rigurosa de la exactitud del método de polinomio único de ahusamiento empleando diferentes datos de árboles apeados.

REFERENCIAS BIBLIOGRÁFICAS

Bi, H. (2000). Trigonometric variable-form taper equations for australian Eucalyptus. Forest Science, 46(3), 397-409.         [ Links ]

Biging, G. S. (1988). Estimating the accuracy of volume equations using taper equations of stem profile. Canadian Journal Forest Resource, 18, 1002-1007.         [ Links ]

Bruce, D., Curtis R., & Vancoevering, C. (1968). Development of system and taper volume tables for red alder. Forest Science, 14, 339-350.         [ Links ]

Campos, J., & Leite, R. (2013). Mensuração Florestal. Universidades Federal de Viçosa, Brasil. 605 p.         [ Links ]

Cancino, J. (2006). Dendrometría básica. Concepción, Chile: Universidad de Concepción. 163 p.         [ Links ]

Cao, Q., Burkhart, E., & Max, T. (1980). Evaluation of two methods for cubic-volume prediction of loblolly pine to any merchantable limit. Forest Science, 26(1), 71-80.         [ Links ]

Corral, R., Návar J. de J., & Fernández, F. (1999). Ajuste de funciones de ahusamiento a los perfiles fustales de cinco pináceas de la región de El Salto, Durango. Madera y Bosques, 5(2), 53-65.         [ Links ]

Cuevas, G. (2008). Ecuaciones de cubicación para el alcornoque del este de Argelia. Forest Systems, 4(1), 119-126.         [ Links ]

Demaerschalk, J. P. (1972). Integrated systems for the estimation of tree taper and Volume. Canadian Journal Forest Resource, 3(90), 90-94.         [ Links ]

Fang, Z., & Bailey, R. (1999). Compatible volume and taper models with coefficients for tropical species on Hainan Island in southern China. Forest Science, 45(1),85-100.         [ Links ]

Figueiredo, F. A., & Budant S. L. (1999). Comparison between predicted volumes by taper equations and true volumes obtained by the water displacement technique (xylometer). Canadian Journal Forest Resource, 29, 451-461.         [ Links ]

Organización de las Naciones Unidas para la Alimentación y la Agricultura (FAO). (1980). Estimación del volumen forestal y predicción del rendimiento con referencia especial a los trópicos: predicción del rendimiento. Estudios FAO: Montes, vol. 22. 92 p.         [ Links ]

Galán, R. De los Santos Posadas, H. M., & Valdez, J. I. (2008). Crecimiento y rendimiento de Cedrela odorata L. y Tabebuia donnell-smithii Rose en San José Chacalapa, Pochutla, Oaxaca, México. Madera y bosques, 14(2), 65-82.         [ Links ]

García, M., Corral, J., Díaz, M., & Martínez, M. (2009). Función de ahusamiento y volumen compatible para Pinus arizonica Engelm. En el suroeste de Chihuahua. Ciencia Forestal en México, 34(105), 119-136.         [ Links ]

García, O. (1995). Apuntes de mensura forestal. Valdivia, Chile: Facultad de Ciencias Forestales-Universidad Austral de Chile. 65 p.         [ Links ]

Hilt, D. (1980). Development of taper functions from variable-top merchantable volume equations. Forest Science, 26(1), 117-120.         [ Links ]

Kleinn, C. (2000). Inventario y evaluación de árboles fuera del bosque en grandes espacios. Unasylva 200, 51(3), 3-10.         [ Links ]

Kozak, A., Munro, A., & Smith, J. (1969). Taper functions and their application in forest inventory. The Forestry Chronicle, 45, 278-283.         [ Links ]

López, A., Barrios, A., & Trincado, G. (2015). Modelos de perfiles fustales con una estructura de error autorregresiva para plantaciones de Eucalyptus tereticornis en Colombia. Madera y Bosques, 21(2), 73-88.         [ Links ]

Mancera, J. (2014). Estudio comparativo de los resultados de cubicación en la especie Eucalyptus tereticornis implementando métodos directos e indirectos utilizando el dendrometro criterion RD 1000 (trabajo de pregrado, Ingeniería Forestal). Bogotá: Universidad Distrital Francisco José de Caldas. 64 p.         [ Links ]

Max, T., & Burkhart, H. (1976). Segmented polynomial regression applied to taper equations. Forest Science, 22(3), 283-289.         [ Links ]

Newnham, R. (1998). A variable-form taper function. Ontario: Petawawa National Forestry Institute. 33 p.         [ Links ]

Ormerod, D. (1973). A simples bole model. The Forestry Chronicle, 49(3), 136-138.         [ Links ]

Parresol, B., Hotvedt, J., & Cao, Q. (1987). A volume and taper prediction system for bald cypress. Canadian Journal of Forest Research, 17, 250-259.         [ Links ]

Parresol, B., & Tomas, C. (1996). A simultaneous density-integral system for estimating stem profile and biomass. Slash pine and Willow Oak. Canadian Journal of Forest Research, 26, 773-781.         [ Links ]

Prodan, M., Peters, R., Cox, F., & Real, P. (1997). Mensura forestal. San José de Costa Rica: Agroamerica. 561 p.         [ Links ]

Riecke, F. (1840). Über die Berechnung des körperlichen Inhalts unbeschlagener Baumstämme. Stuttgart: Metzler. 75 p.         [ Links ]

Zapata, M. (2011). Curso Ecuaciones de conicidad y volumen. Fractovolumen. Cali: Smurfit Kappa Cartón de Colombia. 21 p.         [ Links ]

Zhang, L., Peng, C., Huang, S., & Zhou, X. (2002). Development and evaluation of ecoregion-based tree height-diameter models for jack pine in. Forest Chronology, 78(40), 530-538.         [ Links ]