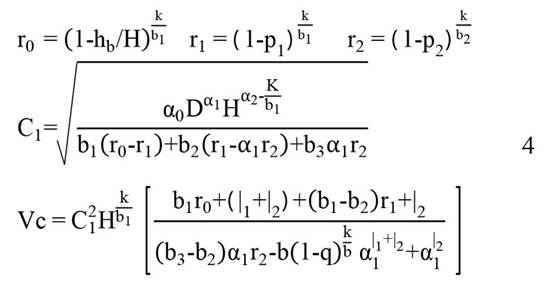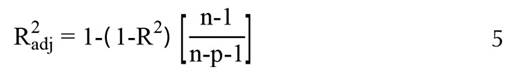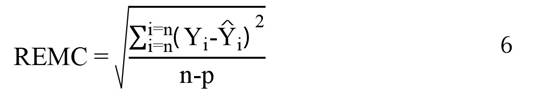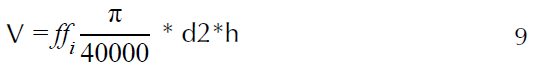Spanish (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
INTRODUCCIÓN
Las actividades silvícolas que se implementan en el bosque tienden a mejorar las condiciones, garantizando de esta manera un alto porcentaje de aprovechamiento en volumen forestal maderable (Valencia-Manzo et al., 2017). Ante esto, las regresiones lineales y no lineales son herramientas que brindan información confiable sobre las variables de interés, facilitando así su análisis e interpretación (Guzmán-Santiago et al., 2020a).
Este tipo de sistemas realizan predicciones de volumen en distintas alturas del árbol, lo que permite hacer clasificaciones de productos, y que se define como la disminución del diámetro con base al aumento de la altura del árbol (Kozak, 1988). Los tipos de modelos se clasifican en árboles individuales, segmentados y de exponente variable (Burkhart y Tomé, 2012), y se caracterizan por ser flexibles y precisos para generar información de volumen comercial de un árbol en pie (Milena-López et al., 2015).
El sistema compatible permite describir los distintos segmentos del árbol, desde un neiloide en la base a formas cilíndricas o paraboloides truncadas (en la zona de mayor aprovechamiento comercial), hasta terminar en su forma cónica o paraboloide en la punta del árbol (Tamarit-Urías et al., 2014), por lo que los diferentes factores ambientales y las actividades silvícolas son claves en la forma geométrica que toma el fuste de cada especie (Uranga-Valencia et al., 2015). Demaerschalk (1972) menciona que se puede tener un modelo compatible siempre que estén definidos los mismos parámetros, así como una estructura geométrica común. Además, por ser de tipo no lineal, facilitan la descripción de los datos de las especies (Urbano et al., 2018).
En este sentido, el modelo de Fang et al. (2000) puede emplearse sin problemas en la planificación forestal, dado que incorpora de manera implícita la ecuación de volumen total de Schumacher y Hall (1933) y, a su vez, puede ser reemplazada por otra similar, según sea conveniente, lo que permite generar una mayor ganancia en el aprovechamiento (Niño-López et al., 2018). El modelo es capaz de describir el conjunto de datos del fuste y el volumen de cualquier especie sin ningún inconveniente (Özçelik y Göçeri 2015; Quiñonez-Barraza et al., 2014), además de las especies tropicales, lo que facilita su incorporación a los sistemas biométricos (López-Martínez et al., 2020).
Durante décadas, diferentes entidades federativas de México han utilizado ecuaciones no apropiadas para cada especie (Cruz-Cobos et al., 2016), por lo que no existe una confianza general en las estimaciones deseadas (Azevêdo et al., 2014). De ahí que varios investigadores e instituciones mostraran interés por generar ecuaciones propias para algunas especies de tipo comercial con la finalidad de apoyar a los manejadores del bosque y, a su vez, obtener información verídica sobre los rendimientos maderables para tomar decisiones sobre su manejo (Vargas-Larreta et al. 2017).
En México, el género Abies es la segunda pinácea maderable, siendo A. religiosa la especie de mayor importancia económica y la más aprovechable, pues contribuye con el 2.8 % de la producción maderable anual (SEMARNAT, 2016). La superficie que ocupa dentro del territorio del país oscila entre 0.07 % y 0.16 %, y su distribución se presenta en forma de parches aislados (INEGI, 2017). Considerando lo anterior, el objetivo del presente estudio fue generar un sistema compatible que permitiera estimar de forma precisa el ahusamiento-volumen comercial, además de analizar los tipos dendrómetricos de Abies religiosa (Kunth) Schltdl. & Cham. en varias regiones de México.
MATERIALES Y MÉTODOS
Área de estudio
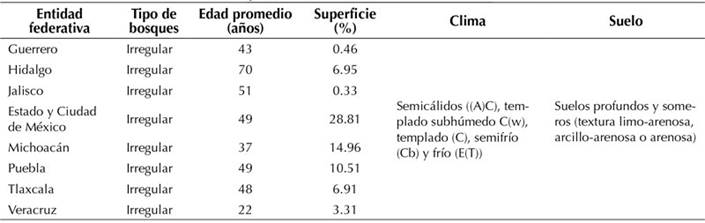
El estudio se desarrolló en ocho entidades federativas que corresponden a 20 Unidades de Manejo Forestal (UMAFOR). Estas fueron: Guerrero (1203), Hidalgo (1303), Jalisco (1404, 1406, 1410), Estado y Ciudad de México (1503, 1507, 1508, 1510), Michoacán (1604, 1605, 1607, 1608), Puebla (2101, 2105, 2108), Tlaxcala (2901, 2902) y Veracruz (3004, 3012) (Tabla 1).
Tamaño de muestra
El tamaño de muestra fue constituido por 2608 árboles de análisis ahusamiento a partir de un muestreo aleatorio por cada UMAFOR en las zonas bajo aprovechamiento forestal y en áreas sin autorización. Para el primer caso se derribaron, seccionaron y midieron cada una de las trozas, mientras que en las áreas no autorizadas se tomaron datos en forma escalonada con una forcípula laser que proporcionó información confiable para hacer la medición del diámetro a distintas alturas (Diéguez-Aranda et al., 2005), considerando en todo momento las diferentes categorías diamétricas. En cada sitio, el diámetro normal fue medido con cinta diamétrica y en ocasiones con forcípulas, y para la medición de las alturas en pie se utilizó un Hipsómetro haga (los árboles derribados se midieron usando el flexómetro). En cada árbol se registraron las variables siguientes: diámetro normal medido a 1.3 m sobre el nivel del suelo (Dn, cm), altura total (Ht, m), diámetros con corteza a diferentes alturas (d, cm) y la altura de la sección del fuste respecto al suelo (hm, m).
Las dos primeras mediciones se realizaron cada 0.30 m por encima del tocón y la tercera hasta el diámetro normal (1.30 m); posterior a esto, las secciones fueron cortadas de manera constante a 2.54 m de longitud hasta un diámetro de sección específico ubicado en la punta delgada del árbol. Las distintas secciones que tienden a la forma de un cilindro y paraboloide fueron cubicadas por la fórmula de Smalian (1), mientras que para la punta del árbol se utilizó la del cono (2). El volumen de fuste consideró la suma de los volúmenes de las trozas.
Donde: Vs = volumen por Smalian (m3); S0 y S1 (cm2) = áreas de las secciones transversales de la troza; L = longitud de la troza (m); Vp = volumen de la última sección del árbol (punta del árbol) (m3); So = área de la base de la última sección del árbol (cm2); Ho = longitud de la última sección del árbol (m).
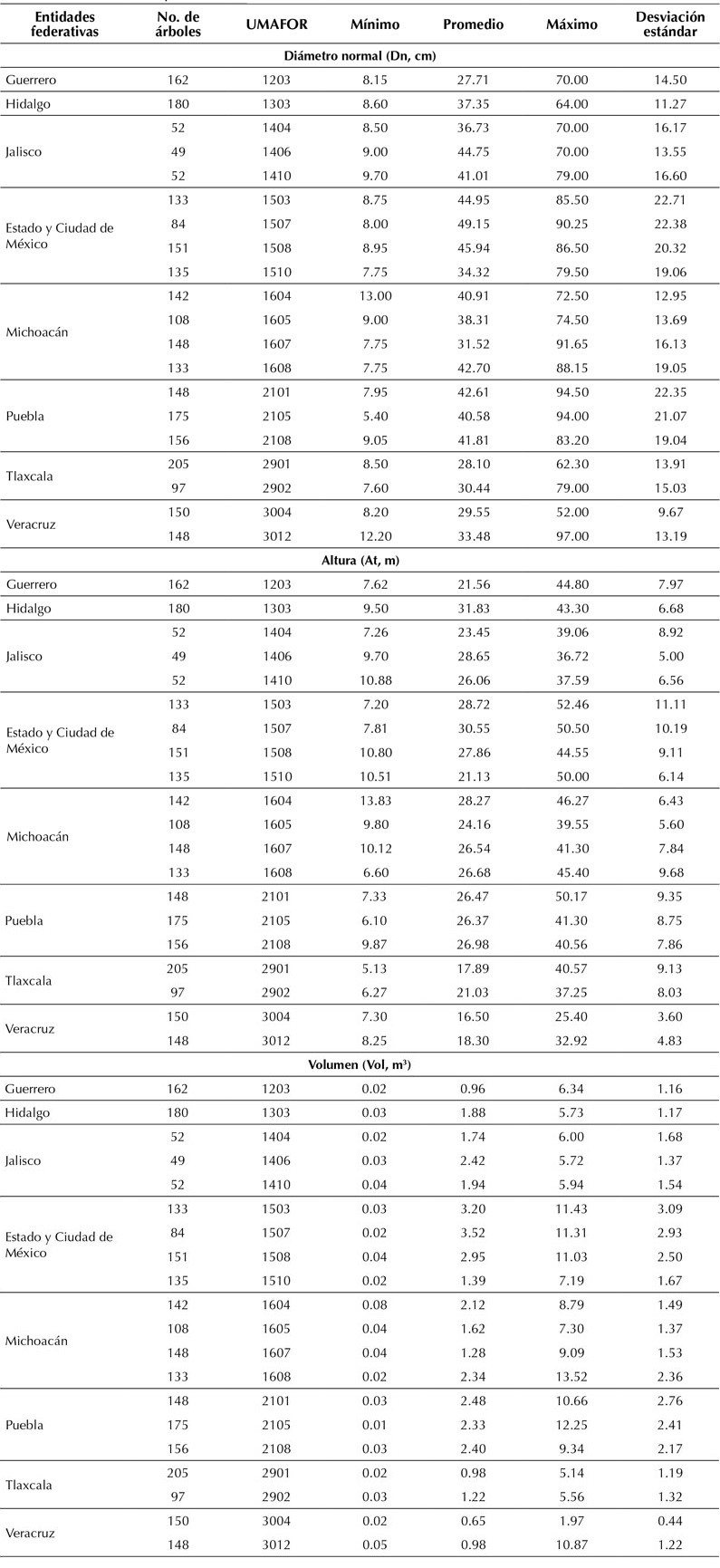
A continuación, se muestran las variables utilizadas para llevar a cabo el ajuste del sistema compatible (Tabla 2).
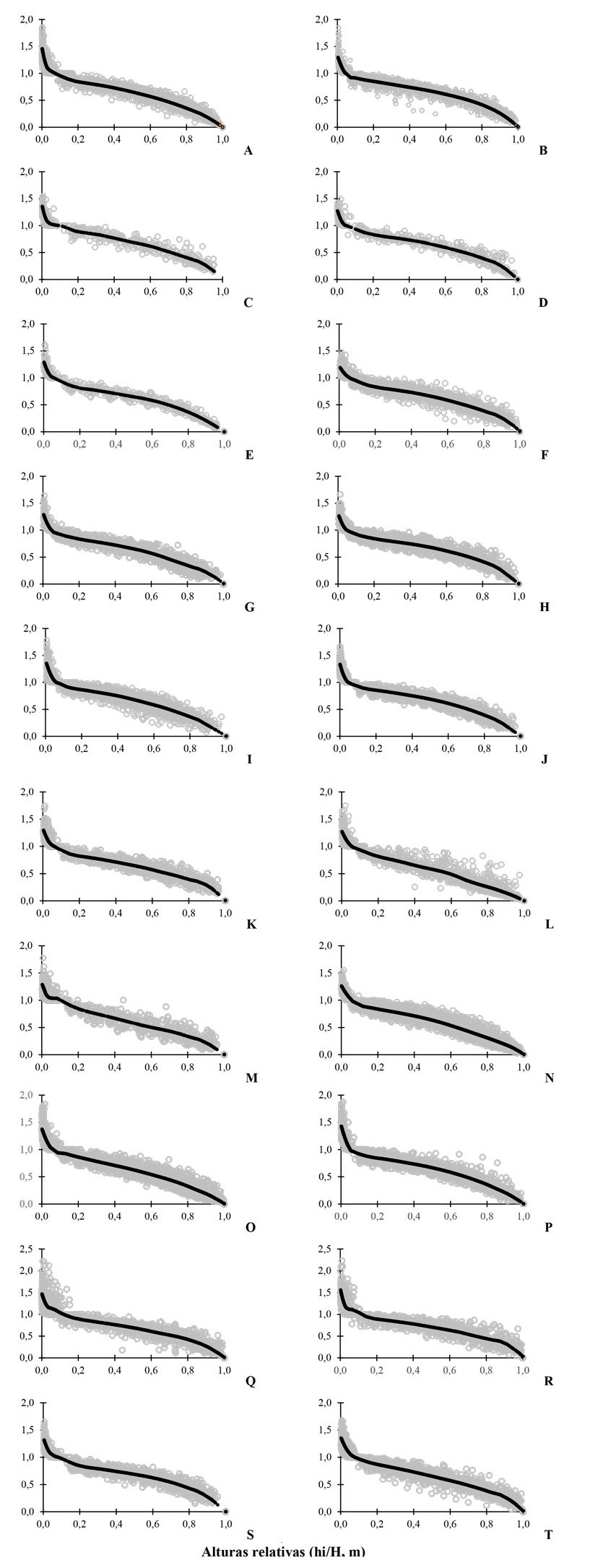
Descripción del perfil de los árboles
Para una mayor comprensión de los datos, se describió el perfil de los árboles mediante el diámetro relativo (d/D, cm) y la altura relativa (hm/H, m) (Figura 1). De igual forma, se realizó el ajuste local cuadrático no paramétrico a través de la regresión local LOESS o LOWESS del paquete estadístico SAS, con un parámetro suavizado de 0.3. Más tarde, los residuales fueron divididos en diez intervalos de altura relativa para observar el comportamiento de los datos (López-Martínez et al., 2020).
Ajuste del sistema
El modelo ajustado fue el de Fang et al. (2000), para describir el perfil del árbol o ahusamiento (3), así como para estimar el volumen comercial (4) por UMAFOR. La función es de tipo polinomial segmentada, está integrada por ecuaciones injertadas y, además, cumple la condición de que h=H, cuando d=0, como se muestra a continuación:
Donde: D = diámetro normal (cm); D = diámetro a la altura h (m) desde el nivel del tocón (cm); H = altura total del árbol (m); hb = altura del tocón (m); Vc = volumen comercial variable (m3); k = π/40000; q = hi-H; αi, bi, pi = parámetros a ser estimados.
Método y bondad de ajuste
Se utilizó el procedimiento MODEL de SAS (SAS Institute Inc, 2008) para la estimación de los parámetros. A través del método de regresión aparentemente no relacionada (RAN) se realizó el ajuste en forma simultánea para minimizar errores de los parámetros.
La eficiencia del modelo para cada UMAFOR se midió mediante los siguientes criterios:
Donde: SCR = Suma de Cuadrado del Error; R2 = coeficiente de determinación; p = número de parámetros a estimar; n = es el tamaño de muestra; ln = logaritmo natural;
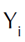= valores observados;
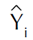= valores predichos.
De manera adicional se realizó un análisis gráfico de los residuos frente a los valores predichos del volumen, ya que es una forma eficiente de evaluar la capacidad de ajuste de un modelo (Guzmán-Santiago et al., 2019).
Corrección de heterocedasticidad
La heterocedasticidad en las funciones volumétricas ocurre porque la varianza en el volumen del árbol crece con las variables explicativas, por lo que se realizó la corrección aplicando una ponderación con los mismos pesos a la inversa de la varianza de cada observación para garantizar las estimaciones de los parámetros. La varianza desconocida se estimó con la función potencial σ2
2 = Υ * Xk. Los valores de Υ y del exponente k se optimizaron empleando los errores del modelo ajustado sin pesos como variable dependiente en el modelo potencial de varianza del error. Finalmente, el peso considerado fue
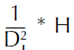para la ecuación de volumen rollo total árbol.
Análisis de los cuerpos dendrómetricos
La flexibilidad del modelo permitió analizar los diferentes segmentos del fuste de los árboles utilizando el siguiente criterio, que consiste en partir de un cuerpo geométrico con una base circular, cuyo valor está dado por d i en cm y la altura definida por h en m:
Donde: ff define el tipo del cuerpo dendrómetrico, es decir, cuando ff~1 es un cilindro; si ff = 0.50 se tiene un paraboloide; cuando ff = 0.33 es un cono; y si ff = 0.25 es un neiloide. En este sentido, el parámetro B i del modelo calcula cada segmento y se obtiene de esta manera:
En consecuencia, se deriva la siguiente expresión para calcular los diferentes puntos del fuste:
Por último, la fórmula que se muestra a continuación permitió calcular el coeficiente de forma con base al promedio B i, aplicable para el modelo de volumen.
RESULTADOS
Bondad de ajuste entre las UMAFOR
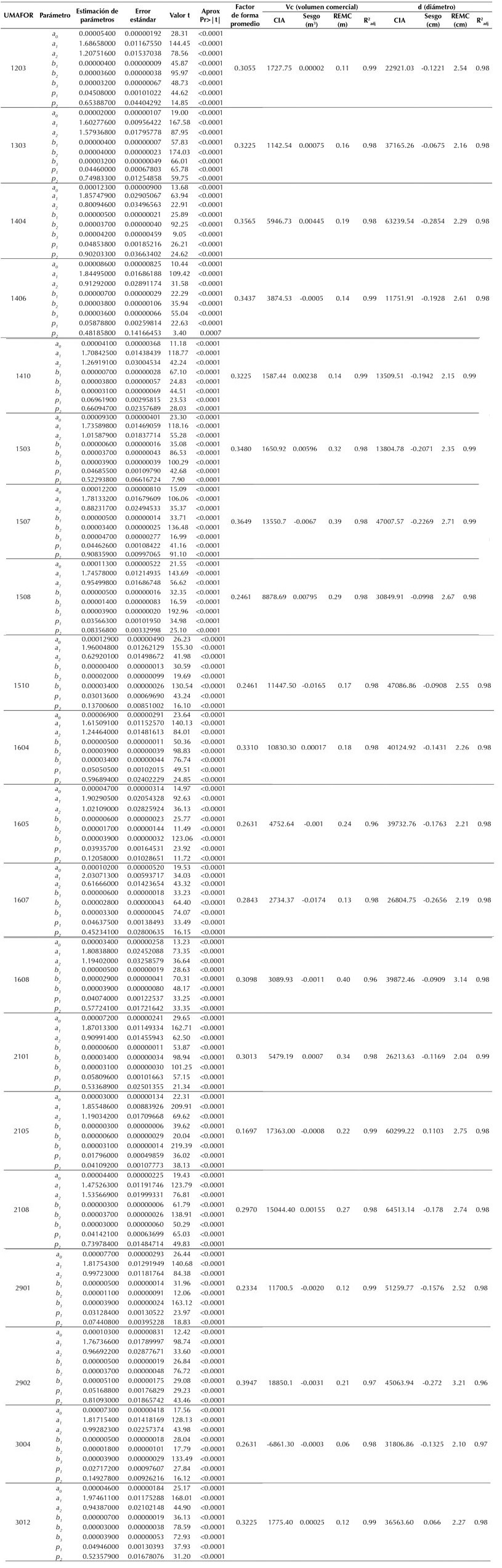
Como se vio en la Tabla 2, los estimadores de cada parámetro fueron reportados con sus respectivas UMAFOR en la forma simultánea, así como la bondad de ajuste generada (ahusamiento, volumen de fuste, volumen comercial, volumen de ramas, volumen total) que resultó altamente significativa (P < 0.0001), lo cual mostró que las variables independientes explicaron más del 97 % del volumen comercial y del ahusamiento. En ambas variables se generaron valores convincentes para describir los conjuntos de datos, evidenciados en el resto de las bondades de ajuste (
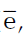REMC y CIA).
Factores de forma entre las UMAFOR
Se obtuvieron resultados con formas geométricas muy semejantes, donde la mayoría se aproximaron del neiloide (tocón) al paraboloide (fuste central) y que ocurren a distintas secciones del fuste (Tabla 3). Por ejemplo, en la UMAFOR 2902 los árboles mostraron un factor de forma donde ff 1 = 0.06 (b 1 ), que tiende al neiloide (arriba del primer punto de inflexión), seguida por la sección media con ff 2 = 0.47 (b 2 ), muy próximo a ser un paraboloide, y la sección superior del fuste (ff 3 = 0.64 (b 3 )) pasa por un paraboloide que tiende aproximarse a un cilindro.
Los casos con valores más bajos en los dos puntos de inflexión (p 1, p 2 ) se dieron para las UMAFOR 1508 (H) con valores de 3.5 % a 8.3 %, 2105 (O) con 1.7 % y 4.1 %, y 3004 (S), que mostró 2.7 % a 14 %, ocurriendo cerca de la base del árbol; excepto para el p 2 de la UMAFOR (S), al ser levemente superior por la unidad de manejo 1605 y 1510. Por el contrario, las zonas con valores más altos para el primer punto fueron las 2101, 1406 (5.8 %) y 1410 (6.9 %). Por otra parte, los primeros valores de p 1 (4.4 % y 4.8 %) fueron similares en las UMAFOR 1404 (C) y 1507 (G) que, sin embargo, arrojaron el segundo punto de inflexión más alto (p 2 = 90 %), describiendo así el cambio geométrico de un neiloide a un cilindro a pesar de que proceden de distintas entidades federativas.
DISCUSIÓN
Los resultados generados permiten modelar la relación ahusamiento-volumen de manera simultánea (Guzmán-Santiago et al., 2020b), lo cual minimiza las pérdidas económicas en la estimación de los datos (Özçelik y Göçeri, 2015). Por ello, la técnica RAN o SUR hace posible obtener estimadores más consistentes y, por ende, coeficientes superiores al 97 %, que son respaldados en otros estudios (Vargas-Larreta et al., 2017).
En cuanto a la información reportada por Vargas-Larreta et al. (2017) en la plataforma SiBiFor durante 2016, para A. religiosa se evidencian buenas estimaciones al tener coeficientes superiores al 96 % (R2) y con una REMC menores a 2.72 cm. Sin embargo, con la calidad de depuración de los datos se logró mejorar los criterios de ajustes ya mencionados, así como de otros añadidos al sistema (CIA y ) sobre existencias de volúmenes totales. Por otra parte, esta investigación se enriqueció al abordar los factores de forma respecto a las variables estimadas en cada uno de los sitios.
En consecuencia, los resultados muestran árboles con formas geométricas que van de un neiloide a un paraboloide con distintos puntos de inflexión, donde se observa que las podas en forma natural ocurren lentamente en los individuos. De ahí que una práctica de manejo bien desarrollada facilite el crecimiento de árboles con tallos rectos y de forma cilíndrica (Quiñonez-Barraza et al., 2014), lo que sería deseable. Aun así, cabe mencionar que la mayoría de los sitios todavía no cuentan con un programa de manejo forestal, o quizás este se encuentra en trámite.
A pesar de tratarse de una sola especie y una serie de factores, sobre todo ambientales, es importante calcular los puntos de inflexión de las distintas regiones dado que difieren entre sí (Berhe y Arnoldsson, 2008). Lo anterior fue propuesto por López-Martínez et al. (2020), quienes investigaron las 11 especies tropicales más importantes del Sureste de México y encontraron resultados similares al explicar más del 94 % sobre la variabilidad en ahusamiento y volumen comercial, así como la tasa de cambios a distintas alturas con base en las procedencias; por ejemplo, de la especie Dendropanax arboreus (L.) Decne. et Planch. encontraron que en las cuatro regiones los primeros puntos de inflexión fueron 6.0 %, 5.7 %, 5.0 % y 7.1 %, mientras que los puntos posteriores indicaron 60 %, 56 %, 57 % y 70 %.
Un resultado parecido se puede observar en el trabajo de Özçelik y Göçeri, (2015) con Eucalyptus grandis Hill ex Maiden y E. camaldulensis Dehnh. en la región de Turquía, al explicar más del 97 % sobre la variable volumen, donde los puntos de inflexión ocurren en 3.6 % y 6.4 % de la altura del árbol, siendo similar a lo encontrado por Sakici et al. (2008) para Abies sp en la misma región. Así mismo, Hernández-Pérez et al. (2013) consiguieron ganancias significativas del 97.06 % y 98.09 % en Pinus patula Schiede ex Schltdl. et Cham., así como puntos de inflexión entre 1.34 % y 82.3 %, y que se asemejan a los resultados de Uranga-Valencia et al. (2015) en los valores de p 1 (1.36 %) y p 2 (96.52 %) en un bosque bajo manejo. Cabe resaltar que el primer punto de inflexión es casi imperceptible dado que se da prácticamente a nivel del tocón. Bajo este mismo enfoque también se aprecian las buenas estimaciones que obtuvieron Martínez-Ángel et al. (2019) para Pinus chiapensis (Martínez) Andresen.
Respecto a los resultados de Pinus cooperi Blanco en Durango, México, se presentan puntos de inflexión aproximado de 4.1 % y 4.6 % (Corral-Rivas et al., 2017; Quiñonez-Barraza et al., 2014), que son semejantes para algunas UMAFOR de esta investigación. A su vez, Fang et al. (2000) reportaron el 54 % para Pinus elliottii Engelm. y 57 % en P. taeda L. en plantaciones de los Estados Unidos. Esta misma metodología ha dado buenas estimaciones en diámetros a distintas alturas de Gmelina arborea Roxb. en Colombia (Niño-López et al., 2018), Eucalyptus tereticornis Smith en Argentina (Milena-López et al., 2015) y E. nitens (Deane et Maiden) Maiden en la región de La Araucanía, Chile (Rodríguez-Toro et al., 2016).
Finalmente, a pesar de que no se percibió ninguna transgresión al supuesto de heterocedasticidad en los datos, se realizó el análisis de corrección, aunque no se encontró mejora en las bondades de ajuste, lo cual se confirma con otros estudios al señalar que en ocasiones no se requiere hacer correcciones (colinealidad, heterocedasticidad y autocorrelación) de las variables ya mencionadas, pues se trata de un modelo segmentado y a veces se pierden ajustes (además de que en la práctica no aporta información de gran relevancia) (Ramírez-Martínez et al., 2018). Es preciso indicar que la varianza no constante en las perturbaciones del modelo es consecuencia de las características biológicas presentes, por lo que no afecta en gran medida durante el ajuste (Prodan et al., 1997).
CONCLUSIONES
Los resultados obtenidos para cada UMAFOR mostraron excelentes estimaciones al hacer uso del modelo segmentado con características biológicas, lo cual facilita la descripción del perfil fustal y del volumen comercial a diferentes alturas.
Con este modelo es posible generar un sistema de ecuación que clasifique los tipos de productos para su comercialización.
A través de esta técnica se puede observar la forma del fuste de la especie, así como los efectos que influyen sobre el ahusamiento, pues depende del manejo del rodal.
En la mayoría de los casos las formas geométricas que toman los árboles van de un neiloide a un paraboloide.
Por último, destacar que es el primer modelo con este tipo de estructura que se genera a nivel de las UMAFOR para las ocho entidades federativas, y que sin duda será de utilidad en los i020nventarios forestales.
