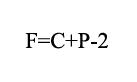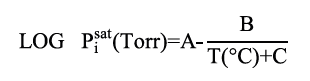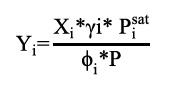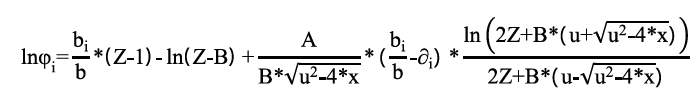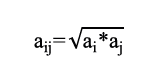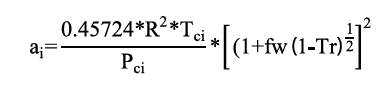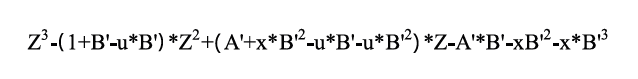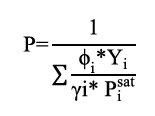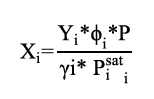La estimación de las condiciones de equilibrio líquido-vapor en mezclas binarias es un tema de interés general para la comprensión del comportamiento de los componentes de una mezcla en equilibrio, que permite la elaboración de diagramas del sistema y que dará las bases para el diseño, análisis y control del proceso de un proceso de destilación, mediante el cual se busca separar las mezclas en componentes puros [1, 2]. El equilibrio líquido-vapor de diferentes mezclas se obtiene comúnmente con pruebas experimentales con el método de destilación, dinámico, de adsorción, entre otros; desarrollados bajo ciertas condiciones de temperatura, presión y concentración [3]. Sin embargo, este tipo de información no puede ser obtenida en todos los casos de forma experimental, ya que los métodos empleados demandan un alto costo de adquisición, relacionados con la necesidad de garantizar puntos con la máxima precisión [2]. Por lo tanto, ha sido necesario elaborar programas computacionales usando ciertos modelos matemáticos para predecir el comportamiento de las mezclas [4,5,6]. El alcance de la presente investigación abarca la programación de modelos termodinámicos y ecuaciones de estado para estimar el equilibrio líquido-vapor en un sistema binario conformado por cloroformo y acetona. Esta mezcla tiene, principalmente, aplicabilidad para la determinación de impurezas mécanicas a muestras de propóleo en laboratorio. Se caracteriza por tener comportamiento no ideal azeótropo a una temperatura de 50 °C [7].
Para ver el equilibrio líquido-vapor de un sistema binario, se construyen curvas P-X-Y, que son gráficas de presión versus la composición de un componente de la mezcla en fase gaseosa y fase líquida. En la elaboración de estas curvas es necesario determinar los coeficientes de fugacidad y actividad. Los coeficientes de fugacidad se pueden obtener mediante ecuaciones de estado [8], tales como: la ecuación Soave-Redlich-Kwong, la cual permite por su simplicidad la determinación del equilibro líquido- vapor (ELV) a altas presiones [9] o la ecuación de Peng Robinson, que fue usada para el desarrollo de este trabajo, ya que predice el equilibrio líquido-vapor con mucha precisión y aproximación a valores experimentales reales, tanto en sistemas binarios como en multicomponentes.
En el cálculo de los coeficientes de actividad se usa la ecuación de Wilson [10], que se basa en el concepto de composición y se caracteriza por ser muy precisa para representar el equilibrio líquido-vapor de sistemas alcohol- hidrocarburo [11] o el modelo de Van Laar, el cual es muy usado por su flexibilidad, simplicidad y capacidad de representar muchos sistemas [12]. Este último fue empleado para el desarrollo de las curvas P-X-Y generadas en este trabajo, puesto que esta ecuación se ha ajustado a los datos de equilibrio líquido - vapor de un sistema binario acetona -cloroformo a una temperatura de 35,17 °C, en trabajos anteriores.
Los resultados de las curvas P-X-Y para un sistema binario cloroformo-acetona, construidas en el presente trabajo a través de la herramienta de software Matlab 9.0, fueron comparadas y mostraron un buen ajuste con errores relativos promedios inferiores a 3,9%, lo que indica la precisión de los modelos termodinámicos y ecuaciones de estado seleccionadas; sin embargo, se recomienda trabajar el mismo sistema con otros modelos para tratar de disminuir el porcentaje de error relativo a valores inferiores al 1%.
Generalidades termodinámicas
Sistemas no-ideales
En la termodinámica existen tres tipos de sistemas: ideales, semi-ideales y no ideales. Los sistemas no ideales se apartan fuertemente en su comportamiento de los modelos que describen los modelos simples y solo se pueden representar mediante métodos de estimación de propiedades termodinámicas que toman en cuenta la interacciones entre partículas. El comportamiento no ideal de un sistema se debe principalmente a su estructura química, la presencia de grupos fuertemente polares en sus moléculas, el gran tamaño de estas, geometría y la posibilidad de ionizarse o asociarse entre sí [12].
En el presente artículo se trabajó con una mezcla no ideal de acetona-cloroformo, la cual tiene grupos polares donde el cloroformo muestra un fuerte desbalance, por el exceso de átomos electronegativos disponibles para formar un puente de hidrógeno; este se debe a que presenta en su composición 3 átomos de cloro frente a un átomo de hidrogeno. Por otro lado, la acetona cuenta con un oxígeno frente a seis hidrógenos [13]. Esta mezcla también es considerada como una disolución azeotrópica, puesto que sus componentes unidos tienen el mismo punto de ebullición, causando que su equilibrio líquido-vapor sea más complejo y por lo tanto, la separación de sus compuestos puros sea imposible de alcanzar mediante método de destilación simple [14,15].
Equilibrio líquido-vapor
Es una condición estática donde no se producen cambios en las propiedades macroscópicas con el tiempo y dinámica a nivel microscópico, ya que las moléculas de la zona líquido están en constante movimiento hacia la zona de vapor y las moléculas de la zona de vapor se mueven hacia la zona de líquido [16].
Para predecir la información respecto al equilibrio líquido-vapor es necesario usar la regla de las fases. Esta permite calcular las fases, grados de libertad o componentes de un sistema para que coexista equilibrio y es expresada mediante la ecuación 1 [17].
Donde
F=Número de grados de libertad
C=Número de componentes del sistema
P=Número de fases en el sistema
En este trabajo se tuvieron dos grados de libertad, debido a que a que se trabajó con un sistema binario y las fases a estudiar fueron dos (líquido y vapor). Esto indica que se fijaron dos variables para definir completamente el estado de equilibrio. Por lo tanto, en el trabajo se estableció la temperatura y composición para determinar la presión del sistema.
Fugacidad y coeficiente de fugacidad
La fugacidad es una propiedad auxiliar estudiada para describir la presión de un gas real. Cuando se hace referencia a un gas ideal se trabaja con presiones parciales; no obstante, para gases reales se trabaja con el concepto de fugacidad, el cual está relacionado directamente con la tendencia de un sistema a preferir una fase frente a otra [18,19,20]. La fugacidad tiene unidades de presión y depende de esta misma.
El coeficiente de fugacidad es la relación que existe entre la fugacidad y la presión del componente como gas ideal [21]. Este se considera como la corrección del estado ideal y sus valores oscilan entre 0 y 1 [22].
Los modelos más conocidos para la determinación de los coeficientes de fugacidad son: Ecuación Virial, ecuación de Van Der Waals, Readlich Kwong, Readlich Kwong- Soave y Peng Robinson [22,23].
Para este trabajo se empleó la ecuación cúbica de estado de Peng Robinson junto con la regla de mezcla cuadrática, ya que a pesar de haber sido postulada hace muchos años, esta se ajusta a varios sistemas y arroja resultados confiables como para ser tomados en cuenta.
Como un ejemplo se muestra en la figura 1 y 2, los resultados obtenidos de calcular los coeficientes de fugacidad con la ecuación de Peng Robinson para los sistemas binarios metano-agua y acetonitrilo– nitrometano, respectivamente. Las figuras muestran bajos niveles de dispersión, respecto a los obtenidos con pruebas experimentales, lo que indica porcentajes de error promedio inferiores al 1% [24].

Figura 1. Comparación de las fracciones molares calculadas con Peng Robinson y obtenidas experimentalmente para un sistema binario metanol-agua.

Figura 2. Comparación de las fracciones molares calculadas con Peng Robinson y obtenidas experimentalmente para un sistema binario Acetonitrilo -Nitrometano.
En la literatura no se encuentra información detallada del modelamiento del equilibrio líquido-vapor de la mezcla acetona-cloroformo con la ecuación de Peng Robinson. Por lo tanto, validar si este modelo representa bien la mezcla estudiada será uno de los principales objetivos y aportes del presente trabajo.
Coeficiente de actividad
El coeficiente de actividad es la medida de la desviación de una disolución respecto al comportamiento ideal. Esta desviación se expresa a través de la función de exceso que depende de la concentración y la temperatura [25].
El coeficiente de actividad se expresa comúnmente a través de ecuaciones tales como: Readlich y Kister (1948) y los modelos de Margules (1985) y Van Laar (1910) [20,26], los cuales se aplican a mezclas binarias, pero no pueden ser extendidos a sistemas multicomponentes [11].
Según la figura 3, la mejor opción para el presente trabajo fue usar el modelo termodinámico de Van Laar, debido a las características de la mezcla cloroformo acetona, ya que esta cuenta con dos componentes polares [27, 22], no electrolitos y la presión de operación se encuentra entre 65 y 80 kPa. Adicionalmente, esta ecuación es muy usada debido a su flexibilidad, simplicidad y capacidad de representar bien muchos sistemas, presentado pequeñas desviaciones con los datos experimentales al modelar los coeficientes de fugacidad de mezclas binarias [28].
Metodología
En esta sección se explica la metodología para la construcción de la curva de burbuja y rocío a partir de los modelos explicados y seleccionados anteriormente, mediante la herramienta de cómputo, Matlab 9.0. El procedimiento está enfocado en un sistema isotérmico, donde se predice el equilibrio líquido-vapor, a través de las presiones para cada una de las relaciones molares establecidas en un sistema binario.
Construcción de la curva de burbuja
En esta primera fase se asumió la composición en fase líquida X1 y X2 (acetona y cloroformo respectivamente) y se supusieron los coeficientes de fugacidad igual a 1(ϕi =1). Posterior a esto, se calculó la presión de vapor (Pisat) para cada componente, usando la ecuación de Antoine a la temperatura de trabajo a través de la siguiente expresión (ecuación 2).
Para el uso de la ecuación 2 se necesitaron las constante de Antoine, A,B y C de cada uno de los componentes de la mezcla analizada (cloroformo, acetona), los cuales se presentan en la tabla 1 [12].
Una vez se definió la presión de saturación para cada componente, se calcularon los coeficientes de actividad (γ1 y γ2) con el modelo de Van Laar a la temperatura de análisis (T) y composición de la fase líquida, a través de las ecuaciones 3 y 4 respectivamente. Las constantes del sistema binario acetona-cloroformo (A12 y A21) son obtenidas de la literatura y corresponden a A12 = -0,8643 y A21 = -0,5899.
Calculados los coeficientes de actividad de la fase líquida y asumiendo los de fugacidad, se procedió a calcular la presión del sistema (P) usando la ecuación 5.
Con la presión calculada se determinaron las fracciones de vapor para cada componente a través de la ecuación 6. Posteriormente, se estimaron los coeficientes de fugacidad para cada componente ϕi , usando la ecuación 7.
Para usar de manera directa la ecuación 7 fue necesario incluir la constante universal de los gases (R) y calcular el coeficiente de fugacidad de cada componente en la mezcla (φi ), el coeficiente de fugacidad en el punto de saturación (φisat) y el volumen de cada componente en el punto de saturación (ViL ).
Como se mencionó anteriormente, el cálculo del coeficiente de fugacidad de los componentes en la mezcla se hizo a través de la ecuación de Peng Robinson (Ecuación 8).
Para la ecuación 8, por tratarse de una mezcla, los parámetros a y b deben ser calculados a través de la regla de mezcla cuadrática. Para este estudio el cálculo se realizó secuencial mentemediante las siguientes ecuaciones (9,10,11).
Donde los parámetros ai y bi son propios de cada componente y se calculan con los puntos críticos de la presión y temperatura (Tci y Pci), mediante la ecuación de Peng Robinson para un componente puro con las ecuaciones 13 y 14.
Para el caso del cálculo del factor compresibilidad (Z) se resuelve el polinomio de la ecuación cúbica generalizada (ecuación 15). Donde x =-2, u=1 y A’ y B’ conforman los coeficientes principales del polinomio.
Para el cálculo de los coeficientes de fugacidad en la zona de saturación se usaron las ecuaciones 7,8,9,10,11,12,13,14, asumiendo cada componente como puro y bajo las condiciones de saturación; es decir, los cálculos se hicieron con la presión de saturación de cada componente, calculada previamente con la ecuación 2.
Para el cálculo del volumen molar saturado de cada componente en fase líquida se empleó la ecuación de Raqquet (ecuación 16), la cual incluye el factor de compresibilidad (Zc ), volumen crítico de cada componente (Vc ) y la temperatura reducida (Tr ).
Con los parámetros calculados previamente, el siguiente paso fue recalcular la presión del sistema con la ecuación 17.
Adicionalmente se estableció una tolerancia de 0,001 entre la presión inicial (P) y la presión recalculada (Pf), evaluada a través de un proceso iterativo. Una vez se logró cumplir con dicha tolerancia, el proceso terminó y se inició el cálculo de la presión del sistema para una nueva fracción de líquido.
Construcción de la curva de rocío
Inicialmente, se estableció la temperatura del sistema T y la composición en fase vapor Y1 y Y2 , se asumieron los coeficientes de fugacidad y actividad igual a 1 y se calculó la presión del sistema con la ecuación 18.
Después, se calculó la composición de la fase líquida preliminar con la ecuación 9 y la presión calculada previamente.
Con las fracciones líquidas determinadas en la ecuación 19, se calcularon los coeficientes de actividad con el modelo de Van Laar en las ecuaciones 3 y 4, esto para calcular nuevamente la presión del sistema con la ecuación 18. Seguido a esto, se determinaron los coeficientes de fugacidad ϕi para cada componente con la ecuación, iniciando la iteración con la presión P.
Con la presión calculada y los coeficientes de fugacidad ϕi , se recalculó la composición de la fase líquida mediante la ecuación 19.
Antes de continuar, fue necesario asegurarse que la suma de las fracciones de líquido fuera igual a 1; de lo contrario, esta debe normalizarse a través de la ecuación 20.
Con las fracciones normalizadas (X_nor) se calcularon nuevamente los coeficientes de actividad con el modelo de Van Laar y se evaluó la diferencia con los calculados inicialmente. Si la diferencia era mayor a la tolerancia establecida (tolerancia=0,001) era necesario volver a calcular los coeficientes de actividad con las ecuaciones 2 y 3 de lo contrario se podía continuar el proceso de recalculó de la presión del sistema a través con la ecuación 17. Esta presión fue comparada con la calculada inicialmente a través de una tolerancia establecida (tolerancia=0,001). Si esta era alcanzada el proceso iterativo terminaba, obteniendo la presión real del sistema; de lo contrario, el programa debía volver a calcular la presión con la ecuación 17.
Esta rutina fue realizada en Matlab 9.0 a una temperatura de 50 °C y 35,17 °C para obtener las curvas y los resultados que se muestran en la siguiente sección.
Análisis de resultados
En la figura 4 se puede observar el equilibrio líquido-vapor para un sistema binario cloroformoacetona a una temperatura de 50 °C, obtenido del programa elaborado con la metodología anteriormente explicada. En esta figura se muestra un sistema azeótropo a la presión mínima 61,33 kPa donde la fracción molar liquida de la acetona es 0,4. Este comportamiento se debe a que los átomos de cloro del cloroformo forman puentes de hidrógeno con la acetona, produciendo fuertes enlaces de unión y presentando mejor afinidad en mezcla que en estado puro [29]. Por esta razón, se aumentan las interacciones entre las distintas moléculas, particularmente entre el oxígeno del carbonilo en la acetona y el hidrógeno del cloroformo [13]. Esto aleja al sistema de un comportamiento ideal bajo estas condiciones, causando una desviación negativa, la cual se da porque los valores de los coeficientes de actividad son menores a 1.
Con el objetivo de comprobar la exactitud de la metodología y del modelo de Van Laar y Peng Robinson, las curvas fueron comparadas con las obtenidas experimentalmente a una temperatura de 50 °C [12] y 35,17 °C [30], y las elaboradas en el simulador de procesos químicos Aspen HYSYS y el programador comercial VLE-calc. Dichas comparaciones se pueden ver representadas en las figuras 5, 8,11 y 12, respectivamente.
En la figura 5 se muestra la comparación entre en diagrama P-X-Y creada en Matlab 9.0 y el obtenido con pruebas experimentales a 50 °C. Los resultados muestran que, desde la presión de saturación del cloroformo hasta la presión de saturación de la acetona, el porcentaje de error relativo fue inferior al 5%, a pesar del desfase entre estos dos diagramas. Esto indica que la metodología usada, los modelos termodinámicos y las ecuaciones de estados seleccionado para su elaboración, logran representar las tendencias y el comportamiento del equilibrio líquido-vapor en una mezcla de acetona-cloroformo a una temperatura de operación de 50 °C con una desviación baja para la presión de rocío y burbuja, principalmente para las fracciones molares de acetona inferiores a 0,4, pero una desviación alta para valores por encima de dicha fracción.

Figura 5. Comparación entre el diagrama P-X-Y para sistema acetona + cloroformo a 50 °C construido en Matlab 9.0 y obtenidas con pruebas experimentales.
La comparación de los valores de la presión de rocío y burbuja, calculados con los valores experimentales determinados a 50 °C, se muestra en las figuras 6 y 7. La figura 6 presenta altos niveles de desviación entre algunos de los valores de presión de rocío calculados y estimados experimentalmente y un bajo coeficiente de correlación lineal (0,80), lo que se traduce en un porcentaje de error relativo promedio de 3,24%. Por otro lado, la figura 7 muestra un mejor nivel de ajuste de los valores de presión de burbuja con un porcentaje de error relativo promedio de 2,5% y un alto valor del coeficiente lineal (0,95).

Figura 6. Comparación de los valores de la presión de rocío calculados con los valores experimentales, determinados a 50 °C.
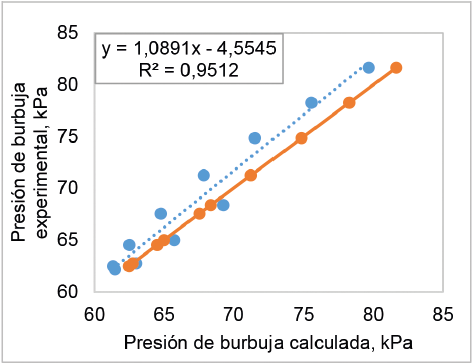
Figura 7 Comparación de los valores de la presión de burbuja calculados con los valores experimentales, determinados a 50 °C.
A continuación, en las figuras 8 se muestra los resultados de comparar los diagramas PXY con los estimados experimentalmente a 35,17 °C. En esta figura se evidencia que la mezcla binaria de acenotacloroformo, a la temperatura de 35,17 °C, presenta un comportamiento azeotrópico a la presión mínima de 34,10 kPa por las mismas razones explicadas anteriormente. También se puede observar que las curvas construidas tienen menor nivel de desfase con los datos experimentales para esta temperatura, que para el caso de 50 °C, causando menor porcentaje de error.

Figura 8. Comparación entre el diagrama P-X-Y para sistema acetona-cloroformo a 31,7 °C construido en Matlab 9.0 y obtenidas con pruebas experimentales.
Lo anterior, también se puede observar en las figuras 9 y 10, donde se presenta la desviación de los valores calculados y obtenidos experimentalmente de la presión de burbuja y rocío, respectivamente. La figura 9 muestra que se tiene un buen ajuste, ya que la mayoría de los datos de la presión de burbuja calculados coinciden con los datos experimentales, causando un porcentaje de error relativo promedio de 1,9% y un alto coeficiente de relación lineal. La figura 10 muestra que los valores de presión de rocío, obtenidos mediante los modelos seleccionados, tienen un menor ajuste con los datos experimentales, causando un porcentaje de error relativo promedio de 2,3%.

Figura 9. Comparación de los valores de la presión de burbuja calculados con los valores experimentales, determinados a 35,17 °C.

Figura 10. Comparación de los valores de la presión de rocío calculados con los valores experimentales, determinados a 35,17 °C.
El análisis de los resultados anteriormente expuestos permite concluir que a pesar de que los porcentajes de error son bajos y se representan las tendencias, el modelamiento nos muestra los porcentajes de error esperados, según lo observados en la literatura (<1%). También, se puede observar que se tiene mejor ajuste de los valores de presión de burbuja para las temperaturas de 35,17 °C y 50 °C, ya que se alcanzan porcentajes de error del 1,9% y 2,3%, respectivamente. Mientras que los valores de presión de rocío obtenidos alcanzaron porcentajes de error del 2,5% y 3,9%. Adicionalmente, estos porcentajes de error indican que las ecuaciones de Van Laar y Peng Robinson logran representar de mejor manera el sistema de cloroformo-acetona al disminuir la temperatura, debido a que con la temperatura de 35,17 °C se obtienen los menores porcentajes de error relativo. Esto se debe a que, al aumentar la temperatura del sistema, incrementa la probabilidad de que los dos componentes coexistan en estado líquido y bajo esta condición, la ecuación de Van Laar pierde precisión para calcular los coeficientes de actividad [31].
En la figura 11 se muestra la comparación del diagrama P-X-Y para el sistema acetonacloroformo construido en Matlab 9.0 y el arrojado por un programador comercial VLE-CALC. Como se puede ver en esta figura, el comportamiento de las dos gráficas sigue la misma tendencia; sin embargo, el creado en Matlab 9.0 sufre una leve sobrestimación en cuanto a las condiciones baja las cuales se da la formación del azeótropo, pero subestimación en el cálculo de la presión de saturación del componente 1 o acetona. Esto se puede dar porque el programador comercial trabaja con diferentes modelos para la construcción de la curva, no obstante, el porcentaje de error relativo promedio del 1%.
En la figura 12 se compara el diagrama de P-X-Y construido en Matlab 9.0 y el creado en Aspen HYSYS. Aspen HYSYS es uno de los simuladores de procesos químicos más conocidos debido a su alta precisión, cuya función es servir de apoyo para el diseño y modelado en la industria. En esta figura se puede ver que los dos diagramas se ajustan muy bien, principalmente a concentraciones bajas de acetona, donde no se ve desfase entre las curvas. También se puede observar que las condiciones bajo las cuales se da la formación del azeótropo son exactamente las mismas; sin embargo, para fracciones molares de acetona superiores a 0,6, el programa creado en Matlab 9.0 subestima el comportamiento de las curvas del equilibrio líquido vapor y esto lleva a que la presión de saturación de la acetona sea diferente.

Figura 11. Comparación entre el diagrama P-X-Y para sistema acetona + cloroformo a 50 °C construido en MATLAB y el arrojado por el programador ELV-CAL.

Figura 12. Comparación entre el diagrama P-X-Y para sistema acetona + cloroformo a 50 °C construido en MATLAB y el creado en Aspen HYSYS.
Bajo los cuatro escenarios de comparación, las curvas tuvieron la misma tendencia y el desfase entre estas fue mínimo; lo que permite asegurar que el programa elaborado para construir las curvas de rocío y curvas de burbuja del equilibrio líquido vapor del sistema binario acetona-cloroformo tiene buen funcionamiento. Sin embargo, se recomienda continuar revisando el mismo sistema con otros modelos y ecuaciones que permitan mejorar el ajuste y alcanzar porcentajes de error inferiores al 1% con respecto a los datos experimentales.
Conclusión
Los resultados obtenidos con la metodología mostrada en este artículo para el modelamiento del equilibrio líquido-vapor, aplicada a un sistema binario (Acetona- cloroformo a 50 y 31,7 °C) no ideal azeótropo, usando el modelo de Van Laar y la ecuación cubica de estado de Peng Robinson, permiten concluir que los porcentajes de error son bajos y logran representar las tendencias; sin embargo, se recomienda continuar revisando el mismo sistema con otros modelos y ecuaciones que permitan mejorar el ajuste con respecto a los datos experimentales.
Con el modelo de Van Laar y la ecuación cúbica de estado de Peng Robinson se tiene mejor ajuste de los valores de presión de burbuja para las temperaturas de 35,17 °C y 50 °C, ya que se alcanzan porcentajes de error promedio del 1,9% y 2,3%, respectivamente. Mientras que los valores de presión de rocío obtenidos alcanzaron porcentajes de error promedio del 2,5% y 3,9%.
Los porcentajes de error indican que las ecuaciones de Van Laar y Peng Robinson logran representar de mejor manera el sistema de cloroformoacetona al disminuir la temperatura, debido a que a 35,17 °C se obtienen los mejores ajustes con los datos experimentales. Esto se debe a que, al aumentar la temperatura del sistema, incrementa la probabilidad de que los dos componentes co-existan en estado líquido y bajo esta condición, la ecuación de Van Laar pierde precisión para calcular los coeficientes de actividad.