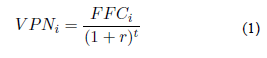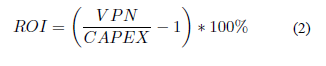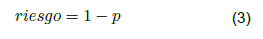Introducción
La situación actual en las reservas de petróleo ha dirigido la atención de las compañías al desarrollo y la aplicación de estrategias para el aumento en la producción en los campos actuales [1-4]. Sin embargo, las afectaciones a los procesos en las áreas de inyección y producción son rutinarias, ocasionando incumplimiento en los objetivos de operación. Debido a esto, los profesionales de economía requieren datos actualizados de los desempeños de los pozos, con los cuales pueden establecer estrategias en busca de metas a mediano y largo plazo, disminuyendo el riesgo financiero [5,6]. En este sentido, el apoyo a la operación del campo A en el Valle Medio del Magdalena (VMM), se dirige al mantenimiento de la producción, por identificación rápida de fallas en los pozos; estas fallas son representadas por disminuciones en los respectivos flujos de crudo. No obstante, factores como los elevados volúmenes de información, la medición manual, el elevado número de pozos en un campo y los costos de implementación de sensores físicos restringen el acceso a los desempeños de los pozos en tiempo real [7,8,10]. De igual manera, la producción en diversos pozos, según el precio del crudo, puede ser insuficiente para justificar una inversión en los hardware de medición de producción en línea [8,11]. Por otra parte, los sensores virtuales (SV) corresponden a modelos fenomenológicos, estadísticos o de inteligencia artificial que predicen variables de proceso (e.g. flujo de producción), utilizando datos de variables que si cuentan con sensores físicos instalados (e.g. temperatura y presión) [5,6,8,10,12,13]. Los SV se presentan como una opción de medición en tiempo real y a bajo costo, que pueden suministrar datos de producción útiles en las labores de mantenimiento preventivo, de planeación y de evaluación, así como estimados de pagos por regalías [5,8-10,14]. El desarrollo y la implementación de estos SV ayudan en la minimización de las inversiones de capital (CAPEX, capital expenditure) y de los costos de funcionamiento (OPEX, operational expenditure) [8-10].
Con lo anterior, la predicción de pozos con fallas (disminución de flujo) puede ser realizada mediante un SV. La comparación de los flujos esperados con los resultados de predicción del SV puede indicar el pozo con requerimientos de mantenimientos correctivos. Es decir, el desarrollo de un SV para la predicción de los flujos de crudo del campo A en el VMM puede proporcionar una ventaja en la operación, por reducción en los tiempos de respuesta en la aplicación de las respectivas correcciones en pro de la normalización de la producción. Tanto el desarrollo como la implementación de los SV han sido reportadas en diversos documentos de literatura. Cai et al. desarrollaron el sistema ESMER MPFM (expert system for multiphase metering) para la predicción del flujo en las líneas de producción, en una plataforma offshore en Malasia [15]. Los autores entrenaron una red neuronal artificial (RNA) con las variables de entrada: patrón de flujo, distribución de fases, densidad, viscosidad y salinidad, entre otras, prediciendo los flujos de producción cada minuto. Cai et al. reportaron un error total de entrenamiento del 10 % para flujos entre 373 y 6 000 bpod [15]. Por su parte, Mirzaei-Paiaman y Salavati propusieron una RNA de predicción de flujo de producción (entre 198 - 9643 bopd), con base en las condiciones de cabeza de 65 pozos, en 15 campos de producción del suroeste de Irán [16]. Los autores entrenaron la RNA con las entradas: presión en la válvula de choke, tamaño de la válvula de choke y relación gas a líquido. Según Mirzaei-Paiaman y Salavati, las predicciones reportaron errores de máximo 6,6 %, mejorando los desempeños obtenidos por correlaciones semiempíricas [16]. De otro lado, Al-Jasmi et al. entrenaron estructuras RNA en la predicción del flujo de producción en pozos maduros, operando con sistemas de levantamiento ESP y por gas [17]. Los autores consideraron las variables de entrada: presión THP, presión FBHP, apertura de la válvula choke, flujo de gas de levantamiento, voltaje, amperaje, PIP y PDP, medidas por un periodo de 90 días. Según Al-Jasmi et al., la predicción reportó errores entre el 5 y el 10 % para pozos con ESP [17]. Por su parte, Ahmadi et al. aplicaron RNA, lógica difusa y algoritmos genéticos en la predicción del flujo de crudo, utilizando información de temperaturas y presiones de líneas de producción de 50 pozos del Golfo Pérsico Iraní [18]. Los autores reportaron una reproducción del 93 % en la varianza de las muestras con la RNA. También, Bikmukhametov y Jäschke revisaron diferentes reportes sobre SV basados en modelos fenomenológicos y de aprendizaje de máquina [10]. Según los autores, la mayoría de los reportes en SV basados en aprendizaje de máquina han aplicado RNA de tipo feedforward. Los autores identificaron oportunidades de desarrollo en SV, particularmente en lo relacionado con predicciones de flujo no estacionario. Por último, George desarrolló un SV basado en RNA para la predicción del flujo de producción del campo Volve en Noruega [13]. La RNA fue entrenada con las variables temperatura y presión de fondo de pozo, presión del anular y los parámetros de la válvula choke. El autor entrenó diferentes arquitecturas, considerando número de neuronas en las capas internas, funciones de activación y algoritmos de aprendizaje. El autor reportó los mejores desempeños de predicción con dos capas internas y función de activación Selu [13].
Las anteriores referencias muestran la factibilidad en la predicción del flujo de producción en diferentes tipos de pozo (sistema de levantamiento y ubicación geográfica), utilizando modelos RNA y datos de operación. Asimismo, la mayoría de las referencias omite los detalles de la arquitectura de las RNA en el SV, así como un análisis económico de la implementación. Con este soporte, el presente documento expone los resultados de un análisis de viabilidad técnico-económico de su implementación de un SV de producción en pozos, con sistema de levantamiento PCP, de un campo del VMM. Este SV fue direccionado a la disminución de los tiempos de respuesta ante las fluctuaciones de la producción. Para esto, diferentes arquitecturas de RNA fueron entrenadas y validadas en la predicción de la producción en los pozos, según los valores históricos de operación, definiendo los desempeños con el estadístico error cuadrático medio (MSE, mean squared error). Posteriormente, los requerimientos tanto de CAPEX como de OPEX fueron definidos para la implementación del SV, con lo cual diferentes índices económicos fueron calculados.
Metodología
Conjunto de datos de producción
El conjunto de datos históricos de producción fue conformado con 980 muestras y 20 variables, referidas a una ventana de operación de dos años, para más de 100 pozos con sistema PCP. Los históricos de operación consideraron, entre otras, las variables, x1: flujo neto (bopd), x2: flujo bruto (bfpd), x3: BSW (%), x 4 : sedimentos (%), xs: nivel (ft), x 6 : nivel sobre bomba corregido (ft), x7: nivel sobre bomba (ft), x 8 : nivel libre de gas (ft), x 9 : profundidad bomba (ft), x10: altura tope (ft), x11: altura base (ft), x12: THP (pressure of the tubing of production), x 13 : CHP (pressure of the casing), x 14 : RPM y x15: torque (lbs/ft). Este conjunto de datos fue depurado, omitiendo muestras con valores faltantes; con esto, el número de muestras Anales fue reducido a 548. Por su parte, el número de variables fue reducido a 15, omitiendo variables cuyos coeficientes de correlación reportaron valores superiores a 0,80. Los datos fueron normalizados entre 0 y 1 para su uso en las RNA.
Arquitecturas y entrenamiento de RNA
La arquitectura de RNA asumida fue la de tipo feedforward, con una capa de entrada, una capa intermedia y una capa de salida; una sola capa intermedia por lo general es suficiente para las predicciones [19]. La capa de entrada consideró 14 neuronas (variables de entrada). Por su parte, el número de neuronas de la capa intermedia fue determinada, según el menor valor de MSE. Las arquitecturas de RNA entrenadas fueron definidas como 14:x:1, en donde 14 se refiere a las neuronas de la capa de entrada, x las neuronas de la capa oculta o intermedia y 1 a la neurona de salida. El número de neuronas ocultas fue variado desde 1 hasta 30 (un poco más del doble de las entradas, según lo recomendado por Berry y Linoff [20]). Las funciones de activación utilizadas en la capa intermedia fueron la tangente hiperbólica (tanh) y la logística (logsig). Para las capas de entrada y salida, la función de activación utilizada fue la lineal (purelin). El conjunto de datos fue dividido en dos subconjuntos, el 70 % de los datos para entrenamiento, mientras el restante fue utilizado en la validación. Los desempeños para cada RNA fueron definidos en términos de los estadísticos MSE y R2, promediados en 15 etapas de entrenamiento-validación, según lo recomendado por Swingler [21].
La función neuralnet (paquete Neuralnet) del programa de uso libre R fue aplicada para el entrenamiento y la validación de las RNA. En la ejecución de esta función, las opciones: algoritmo de entrenamiento con prevención del sobreajuste, función de error MSE, funciones de activación (logsig o tanh) y número de neuronas, fueron especificadas para cada estructura de RNA. Una explicación más detallada de las opciones y el algoritmo de la función neuralnet puede ser encontrada en el trabajo de Zhang [22].
Análisis Económico
El CAPEX fue calculado como el costo del profesional encargado de la codificación del SV en el sistema de gestión de datos. El perfil profesional seleccionado fue el de Maestría, con un tiempo de contratación de un mes. El costo respectivo al profesional fue tomado de la Guía de Aspectos Laborales de ECOPETROL S.A. Por su parte, el costo OPEX consideró el mantenimiento del SV. Este mantenimiento corresponde al análisis de un nuevo conjunto de datos y al reentrenamiento de la RNA; la calibración de la RNA del SV es requerida como cualquier sensor físico [6,15,23]. El tiempo estimado para el mantenimiento fue de un mes, aplicado dos veces al año. De otro lado, para los ingresos, según la literatura consultada, los sistemas de medición inteligentes conducen a una disminución en los tiempos de respuesta de hasta 70 %, ante situaciones de falla en pozos del petróleo. Con la disminución en los tiempos de respuesta, los pozos pueden incrementar su producción en hasta 12 % [12,24,26]. Por consiguiente, un aumento de 10 % en la producción, derivados de la aplicación del SV, fue asumido para la evaluación económica. Por su parte, la producción fue reducida considerando una tasa de declive anual del 14 % (esto en ausencia de nuevos pozos) para un flujo de caja de 10 años. Un valor promedio de $ 60,9 usd/barril fue tomado para la referencia Brent. Además, el flujo de caja incluyó los costos incrementales directos de producción del campo (FLC: field lifting costs), por un valor de $ 17,48 usd/ barril. Asimismo, el EBITDA (earnings before interest, taxes, depreciation and amortization) fue calculado con la resta entre la ganancia neta incremental y los OPEX. El flujo neto de caja fue determinado con la resta entre el EBITDA y el impuesto de renta (33 %). Por su parte, el TRM promedio correspondió a $ 3910,6 pesos m.c. La inflación asumida para todo el proyecto fue del 5,6 % (promedio últimos 5 años). Los indicadores económicos calculados correspondieron al valor presente neto (VPN), la tasa interna de retorno (TIR) y el retorno de la inversión (ROI). El VPN fue calculado con la resta entre los flujos de egresos y los flujos de ingreso, en valor presente, resultantes de la aplicación del proyecto, según [27,28],
Donde VPN i , FFC 1 r y t corresponden, en su orden, al valor presente neto del flujo futuro de caja i, al valor futuro del flujo futuro de caja i, a la tasa de interés y al tiempo del flujo de caja. El VPN i se determina con la suma de todos los VPN. . La TIR fue determinada como la tasa para la cual el VPN reportó el valor de cero [28]. Por su parte, el R0I fue calculado con el VPN, según [29],
Con la Ecuación 2, los valores positivos de ROI representan retornos superiores del doble de la inversión.
Resultados
Estadísticas del conjunto de datos
La Tabla 1 presenta la matriz de los coeficientes de correlación entre pares de variables del conjunto de datos. Según esta tabla, las variables muestran baja correlación entre ellas. Con esto, el flujo neto de crudo producido (x 1 ) debe ser predicho utilizando una combinación entre las demás variables (i.e. ninguna de las variables, por sí sola, predice x 1 con significancia estadística). Los signos positivos y negativos de los coeficientes refieren una relación directa o inversa, respectivamente. Según los datos, un mayor valor de BSW (x 3 ) tiende a generar un menor valor de x1 Asimismo, algunos pares de variables presentan coeficientes, que reflejan una dependencia leve; es el caso del nivel (x 5 ) con el nivel sobre perforación (x 6 ) y con la profundidad de la bomba (x9), el flujo bruto (x 2 ) y el torque (x 15 ), así como el tope (x) y la profundidad de la bomba (x10), parejas de variables que exhiben valores de coeficientes absolutos superiores a 0,7. Los valores de los coeficientes de correlación entre pares de variables, expuestos en la Tabla 1, justifican la aplicación de las RNA [30]. La falta de una correlación sugiere un aporte de las 14 variables en la predicción de la varianza de x1.
Tabla 1 Matriz de correlación de las variables utilizadas en las RNA.
| X 1 | X 2 | X 3 | X 4 | X 5 | X 6 | X 7 | X 8 | X 9 | X 10 | X 11 | X 12 | X 13 | X 14 | X 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X 1 | 1,00 | ||||||||||||||
| X 2 | 0,46 | 1,00 | |||||||||||||
| X 3 | -0,33 | 0,45 | 1,00 | ||||||||||||
| X 4 | -0,11 | -0,04 | 0,09 | 1,00 | |||||||||||
| X 5 | 0,24 | 0,05 | -0,29 | -0,12 | 1,00 | ||||||||||
| X 6 | -0,20 | -0,02 | 0,18 | 0,09 | -0,72 | 1,00 | |||||||||
| X 7 | -0,09 | -0,07 | 0,05 | 0,06 | -0,55 | 0,69 | 1,00 | ||||||||
| X 8 | 0,32 | 0,03 | -0,25 | -0,08 | 0,19 | -0,24 | -0,03 | 1,00 | |||||||
| X 9 | 0,21 | 0,01 | -0,30 | -0,10 | 0,75 | -0,31 | 0,13 | 0,20 | 1,00 | ||||||
| X 10 | 0,12 | 0,05 | -0,21 | -0,07 | 0,63 | 0,08 | -0,02 | 0,01 | 0,73 | 1,00 | |||||
| X 11 | 0,32 | 0,17 | -0,22 | -0,06 | 0,34 | -0,20 | -0,05 | 0,23 | 0,37 | 0,26 | 1,00 | ||||
| X 12 | 0,14 | 0,10 | 0,04 | -0,03 | 0,11 | -0,09 | -0,03 | 0,18 | 0,10 | 0,06 | -0,03 | 1,00 | |||
| X 13 | -0,09 | -0,08 | 0,02 | 0,06 | -0,06 | 0,07 | 0,03 | -0,04 | -0,05 | -0,01 | 0,03 | 0,00 | 1,00 | ||
| X 14 | 0,28 | 0,51 | 0,18 | -0,03 | 0,11 | -0,04 | 0,05 | 0,08 | 0,17 | 0,12 | 0,10 | 0,10 | 0,00 | 1,00 | |
| X 15 | 0,33 | 0,70 | 0,30 | -0,05 | 0,28 | -0,21 | -0,24 | 0,08 | 0,15 | 0,17 | 0,24 | 0,16 | -0,13 | 0,21 | 1,00 |
Entrenamiento y validación de estructuras de RNA
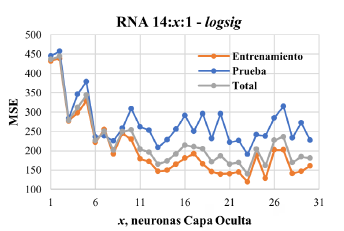
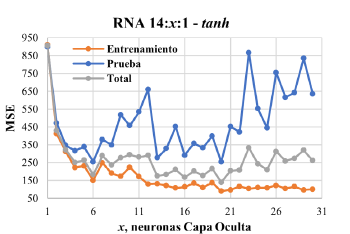
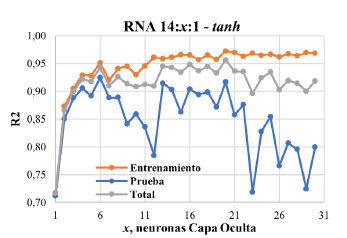
Las Figuras 1 y 2 presentan los resultados de los entrenamientos y las validaciones de las RNA 14:x:1 - tanh, en términos de los estadísticos MSE y R2, respectivamente. De igual manera, las Figuras 3 y 4 muestran los resultados para las RNA 14;x:1 - logsig. De las Figuras 1 y 3 es posible inferir una mejora en el estadístico MSE con el aumento en el número de neuronas intermedias (x), para las dos funciones de activación (logsig y tanh). Por el contrario, el MSE de las etapas de validación exhibe una desmejora paras las RNA con función tanh. La función logsig conduce a una mayor concordancia entre los MSE de validación y de entrenamiento, comparada con los valores resultantes de la función tanh. Esta cercanía en desempeños entre las etapas de entrenamiento y validación manifiesta una mayor confianza en la RNA con logsig para su aplicación en predicciones con diferentes conjuntos de datos [10,31]. Según las Figura 2 y 4, el estadístico R2 de entrenamiento y total (promedio) presenta una tendencia creciente con x para las dos funciones de activación. Sin embargo, para el caso de la función logsig, el R2 reporta un comportamiento errático que afecta el desempeño reportado para 2, 4, 5 y 10 neuronas (valores por debajo de 0,9). Para la función tanh, el comportamiento errático reporta desempeños por debajo de 0,9 para la mayoría de los valores de x, reportando incluso R2 menores de 0,8 en la etapa de validación.
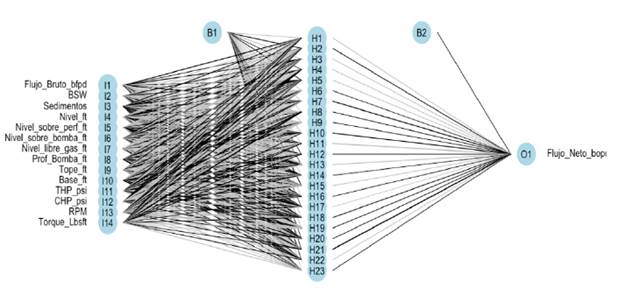
Los desempeños en la etapa de validación son importantes debido a que las RNA entrenadas (con los valores de peso definidos) son probadas con un conjunto de datos diferentes al de entrenamiento (i.e. ya en aplicación). En este sentido, el uso de la función de activación logsig conlleva a un mejor desempeño en las predicciones de las RNA. El mejor desempeño de predicción con logsig lo reporta la red con 23 neuronas (es decir 14:23:1 - logsig), obteniendo R2 total= 0,956 y MSEtotal = 140,6. Por su parte, con la función tanh, el mejor desempeño es alcanzado con 20 neuronas (14:20:1 - tanh), reportando R2 total =0,956 y MSEtotal =139,8. A pesar, del mejor valor de MSEtotal de la red 14:20:1 - tanh, el comportamiento errático de las RNA con tanh en validación, desfavorece su selección para un SV; en recalibraciones posteriores, este comportamiento puede conducir a una pérdida en el desempeño de predicción. Con lo anterior, la red 14:23:1 - logsig corresponde a la red más recomendada para el SV. La Figura 5 muestra la arquitectura para esta RNA.
Sensor virtual
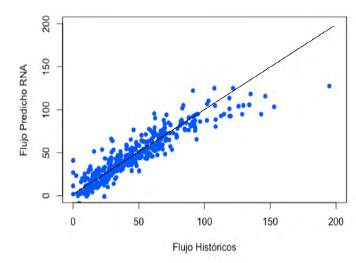
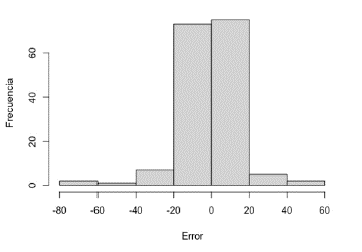
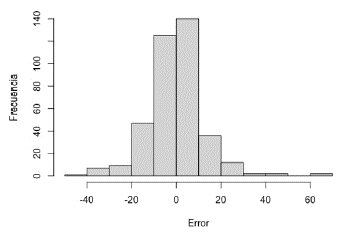
Las Figuras 6 y 7 presentan los gráficos de paridad de flujo neto de crudo predicho con la RNA 14:23:1- logsig versus los históricos, para las etapas de entrenamiento y validación, respectivamente. Según estos gráficos, la predicción con la RNA 14:23:1 - logsig exhibe una distribución alrededor de la línea de 45°; lo anterior manifiesta el seguimiento de la tendencia contenida en los históricos. Esta distribución es confirmada por los histogramas de distribución de errores (histórico- predicho) presentados en las Figuras 8 y 9. Según estas figuras, los histogramas para las etapas de entrenamiento y validación muestran una distribución gaussiana alrededor del valor de 0 bopd. Según Sadri et al. una distribución gaussiana de errores conduce a predicciones aceptables de flujos de producción en pozos de petróleo [32], lo cual valida la predicción con la 14:23:1 - logsig.
Desde luego, tanto las gráficas de paridad como los histogramas de errores presentan predicciones alejadas de los valores históricos (colas izquierda y derecha en los histogramas, Figuras 8 y 9). Sin embargo, más del 90 % de las predicciones presentan errores alrededor de 0 bopd (entre ± 20 bopd); las predicciones de la RNA con mayores errores pueden deberse a situaciones operativas de los pozos (estados inestables por mantenimientos correctivos). Es importante mencionar que los errores reportados por la RNA 14:23:1 - logsig presentan ordenes de magnitud cercanos a varios equipos de medición [32]. Los sensores comerciales de flujo de producción exhiben una exactitud entre el 5 y el 10 %, requiriendo de mantenimiento y calibración constantes [11,23,32,33]; la exactitud puede ser disminuida con sensores comerciales de mayor tecnología, elevando apreciablemente el costo de la inversión y los costos de mantenimiento [11]. Con lo anterior, en términos generales, un SV puede ser programado utilizando la red 14:23:1 -logsig, con lo cual los errores se encontrarán entre ± 23,7 bopd del valor predicho (95 % de confianza). Esta incertidumbre de ± 23,7 bopd corresponde a un error de ± 9,6 % (95 % de confianza) del valor del flujo predicho. La exactitud puede ser incrementada con la aplicación de un algoritmo de reconciliación de datos, disminuyendo los errores sistemáticos (calibración de sensores físicos y estados dinámicos) en el conjunto de datos [34] y/o por una selección de variables para la RNA por aplicación de técnicas de análisis de influencia [35,36].
El SV con la RNA 14:23:1 - logsig puede ser utilizado en la predicción de los flujos de los pozos del campo del VMM. Por comparación con el valor predicho puede ser posible la predicción de pozos con fallas o disminución de flujo. Esta identificación proporciona una ventaja en la operación, debido a que puede reducir los tiempos de respuesta en la aplicación de las respectivas correcciones o mantenimientos para la normalización de la producción, con la respectiva disminución en las diferidas [12,25,26].
Flujo de caja
La Figura 10 presenta los costos de mantenimiento por barril incremental producido diario, resultante de la aplicación del SV con la RNA 14:23:1 - logsig. Según esta figura, los costos de mantenimiento por barril incremental día presentan un aumento durante la vida de evaluación del proyecto; los costos de mantenimiento incrementales inician en $ 5 usd y Analizan en $ 71 usd, un aumento de 12 veces. Lo anterior es una consecuencia de la tasa de declive y del bajo flujo neto de producción diario reportado para el campo del VMM. Considerando la producción anual, los costos de mantenimiento del SV por barril resultan insignificantes, entre $ 0,04 y 0,17 usd/barril, característicos de proyectos de aplicación de SV [7,9]. Por comparación, Zuluaga-Álvarez en 2020 [37] estimó una inversión total de ca. $ 6,6 MMusd y unos costos de mantenimiento de $ 66 Musd anuales para la implementación de 86 sensores de flujo tipo magnéticos de reluctancia variable (frecuencia variable entre 0-15 kHz, amplitud entre 8-190 VP-P y convertidor de frecuencia a corriente directa FDC) en pozos del campo Casabe ubicado en el VMM. La aplicación de los datos de Zuluaga-Álvarez al presente documento, cambiando el SV por sensores reales, conduciría a unos costos de mantenimiento incrementales diarios entre $ 107 usd y $ 646 usd, equivalentes a $ 0,3 y 1 usd/barril por mantenimiento anual; estos valores se encuentran por encima de lo estimado para el SV.
La Tabla 2 exhibe el flujo de caja correspondiente al proyecto de aplicación del SV, para la predicción de los pozos con fallas en producción (pozos con sistema de levantamiento PCP), en el campo del VMM. Con este flujo de caja, los valores determinados para los indicadores económicos corresponden a: VPN = $ 25,6 MMusd, TIR >> 100 % y ROI >> 100 °%. Estos indicadores económicos favorables son consecuencia de la baja inversión (CAPEX) y de los costos bajos de mantenimiento (OPEX). Lo anterior conlleva a una factibilidad económica para la aplicación del SV, basado en la RNA 14:23:1 - logsig. Por su parte, tomando como base lo reportado por Zuluaga-Álvarez [37] y los supuestos de la sección "Análisis Económico", los indicadores resultantes de la implementación de sensores reales reportan valores de VPN = $ 2,4 MMusd, TIR= 39 °% y ROI = 9 %. Comparando los indicadores económicos, la implementación del SV presenta mayores beneficios que la implementación de los sensores reales (ca. 20 veces considerando el VPN).
De otro lado, la inclusión del riesgo en la predicción con el SV puede ser determinado con [28],
Donde p es la probabilidad de éxito en la predicción del SV, la cual puede ser definida con el estadístico R2 de la red 14:23:1 - logsig (R2 total=0,956). Con este valor, el riesgo corresponde a 0,044. Este valor de riesgo fue considerado en el flujo de caja, modificando lo referente a los ingresos por el aumento en la producción. Con el nuevo flujo de caja, los indicadores económicos fueron recalculados, reportando los valores de VPN $ 23,3 MMusd, TIR >> 100 °% y ROI >> 100 °%. Lo anterior conlleva a que el riesgo considerado, disminuya el indicador VPN en un valor de $ 2,2 MMusd (8,6 °%), comparado con el flujo de caja sin riesgo de predicción (Tabla 2). No obstante, con el riesgo incluido, la inversión presenta factibilidad económica para la aplicación del SV en la predicción de los flujos netos de pozos con PCP en el campo del VMM.
Tabla 2 Flujo de caja ($ Musd/año) derivado de la implementación del SV RNA 14:23:1 - logsig.
| Año 1 | Año 2 | Año 3 | Año 4 | Año 5 | Año 6 | Año 7 | Año 8 | Año 9 | Año 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Ingreso Incremental | $ 7935 | $ 13649 | $ 11738 | $ 10095 | $ 8682 | $ 7466 | $ 6421 | $ 5522 | $ 4749 | $ 4084 |
| Manteni. | $ - | $ 7,6 | $ 8,0 | $ 8,4 | $ 8,9 | $ 9,4 | $ 9,9 | $ 10,5 | $ 11,1 | $ 11,7 |
| FLC | $ 2278 | $ 3918 | $ 3369 | $ 2897 | $ 2492 | $ 2143 | $ 1843 | $ 1585 | $ 1363 | $ 1172 |
| Total | $ 2278 | $ 3925 | $ 3377 | $ 2906 | $ 2501 | $ 2152 | $ 1853 | $ 1595 | $ 1374 | $ 1184 |
| EBITDA | $ 5658 | $ 9724 | $ 8361 | $ 7189 | $ 6181 | $ 5314 | $ 4568 | $ 3926 | $ 3375 | $ 2900 |
| EBIT | $ 5658 | $ 9724 | $ 8361 | $ 7189 | $ 6181 | $ 5314 | $ 4568 | $ 3926 | $ 3375 | $ 2900 |
| Impuesto, 33 % | $ 1867 | $ 3209 | $ 2759 | $ 2372 | $ 2040 | $ 1754 | $ 1507 | $ 1296 | $ 1114 | $ 957 |
| Flujo operacional | $ 3791 | $ 6515 | $ 5602 | $ 4817 | $ 4141 | $ 3560 | $ 3061 | $ 2631 | $ 2261 | $ 1943 |
| Inversiones | -$ 3,6 | $ - | $ - | $ - | $ - | $ - | $ - | $ - | $ - | $ - |
| Flujo neto | $ 3787 | $ 6515 | $ 5602 | $ 4817 | $ 4141 | $ 3560 | $ 3061 | $ 2631 | $ 2261 | $ 1943 |
Conclusiones
Los pozos con posibles fallas operacionales en el campo del Valle Medio del Magdalena pueden ser identificados por medio de las predicciones de un sensor virtual de flujo de producción, basado en redes neuronales artificiales y en históricos de operación. La arquitectura de red neuronal con los mejores desempeños correspondió a la definida con una capa de entrada de 14 neuronas (función de activación lineal), una capa intermedia con 23 neuronas (función de activación logística sigmoidal) y una neurona en la capa de salida (función de activación lineal). Los desempeños de esta red reportaron valores de MSEtotal = 140,6 y R2 total = 0,956. Asimismo, la red presentó errores de predicción de ± 23,7 bopd al 95 °% de confianza. La aplicación de un sensor virtual de flujo, basado en esta red, conllevaría a costos incrementales diarios por mantenimiento entre $ 5 y $ 71 usd, con un beneficio económico favorable, dado por los indicadores VPN = $ 25,6 MMusd, TIR >> 100 °% y ROI >> 100 °%, para un flujo de caja de 10 años. Estos valores muestran una superioridad económica comparados con los resultantes de la implementación de sensores reales, con costos incrementales diarios por mantenimiento entre $ 107 y $ 646 usd e indicadores VPN = $ 2,4 MMusd, TIR = 39 °% y ROI = 9 °%. La consideración del riesgo en la predicción del sensor virtual conlleva a una disminución del VPN en cerca del 8,6 °%. Con lo anterior, la implementación de un sensor virtual de producción en pozos PCP del campo del Valle Medio del Magdalena muestra una viabilidad tanto técnica como económica.