Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Lecturas de Economía
Print version ISSN 0120-2596
Lect. Econ. no.65 Medellín July/Dec. 2006
Análisis de los factores asociados a la deserción y graduación estudiantil universitaria
Analysis of the Associated Factors to Drop-Out and College Graduation
Une analyse des facteurs associés a la désertion et à la réussite scolaire dans les universités
Elkin Castaño, Santiago Gallón, Karoll Gómez y Johanna Vásquez *
* Elkin Castaño Vélez: docente, investigador y coordinador del Grupo de Econometría Aplicada " GEA" , Centro de Investigaciones Económicas " CIE" , Universidad de Antioquia. Dirección electrónica: elkincv@gmail.com. Ciudad Universitaria, bloque 13, apartado aéreo 1226, Medellín,
Introducción. I. Modelos de duración para datos agrupados. II. Datos. III. Resultados. IV. Pruebas de diagnóstico. V. Conclusiones y recomendaciones. Anexo. Bibliografía.
Resumen: Las altas tasas de deserción y bajas tasas de graduación se han convertido en un asunto de creciente interés para las instituciones de educación superior y las autoridades educativas. A partir de 2003, la Universidad de Antioquia inició un proceso de identificación de los principales factores asociados a dicho fenómeno. En este artículo se presenta el análisis sobre los determinantes de la deserción y graduación en dos de sus facultades, realizado a partir de la aplicación de los modelos de riesgo proporcional de Prentice y Gloeckler (1978) y Meyer (1990), en tiempo discreto. Los resultados confirman el impacto conjunto que tienen los factores individuales, socioeconómicos, académicos e institucionales sobre la deserción y la graduación.
Palabras clave: riesgo proporcional, modelo de duración en tiempo discreto, heterogeneidad no observada, censuramiento, deserción y graduación estudiantil. Clasificación JEL: C41, C24, I2.
Abstract: High drop-out rates and low graduation rates have become an issue of growing interest for higher education institutions and academic authorities. Since 2003, the University of Antioquia started a process of identification of the main factors associated with this phenomenon. This article presents an analysis of the determinants of drop-out and graduation in two of its schools, carried out by an application of the proportional hazards models of R. Prentice, L. Gloeckler, and B. Meyer set in discrete time. The results confirm the joint impact of individual, socioeconomic, academic, and institutional factors over the risk of dropping out and graduating.
Keywords: proportional risk, discrete time duration model, non-observed heterogeneity, censorship, student desertion and graduation.
Résumé: Un sujet de préoccupation croissante dans les institutions d' éducation supérieure porte sur le taux élevé de désertion scolaire ainsi que sur le faible taux d' obtention des diplômes. L' Université d' Antioquia a entamé depuis l' année 2003 une étude qui cherche à identifier les principaux éléments associés à ce phénomène. Dans cet article, nous présentons les facteurs qui sont à l' origine de ces deux problèmes au sein des deux unités de formation académiques de cette université. Pour ce faire, nous utilisons deux modèles à risque proportionnel en temps discret, celui de R. Prentice et L. Gloeckler et celui de B. Meyer. Les résultats de cette étude signalent l' impact simultané des facteurs socio-économiques, académiques et institutionnels sur la désertion et sur l' échec scolaire.
Mots clés: risque proportionnel, modèles à temps discret, hétérogénéité non observée, désertion scolaire, échec scolaire.
Introducción
Pese al reconocimiento general de los efectos positivos sobre los retornos privados y sociales de la educación, en particular de la educación superior, las tasas cada vez más altas de deserción y bajas de graduación se han convertido en un problema de creciente interés no sólo para las instituciones de educación superior, sino también para las autoridades educativas debido a sus consecuencias socio-económicas.1 De una parte, la larga duración de los estudios de pregrado, además de generar mayores costos privados a los estudiantes, y gastos extras en el caso de las instituciones de educación superior públicas, implica un retraso en la entrada al mercado laboral generando costos sociales y económicos. Así mismo, la pérdida de estudiantes causa a las universidades serios problemas financieros al producir inestabilidad en la fuente de sus ingresos (Tinto, 1989)2; sin embargo, la deserción estudiantil se torna aún más preocupante ya que ésta puede comprometer el futuro de un país en el mediano y largo plazo, al ser la acumulación de conocimiento científico y tecnológico uno de los factores determinantes del desarrollo socioeconómico de una nación.3
Aunque muchas teorías han sido desarrolladas para explicar las decisiones del estudiante a lo largo de su ciclo académico, solo los modelos teóricos de Tinto (1975) (Modelo de Integración Estudiantil " Student Integration Model" ) y de Bean (1980) (Modelo de Desgaste Estudiantil " Student Attrition Model" ) han ofrecido una estructura consistente para entender los factores que afectan tales decisiones (Cabrera, et al., 1993). Tinto, basado sobre el trabajo de Spady (1970), argumenta que la integración y la adaptación social y académica del estudiante en la institución determinan la decisión de permanecer o no en sus estudios. Bean (1980), con una visión más general, considera que la decisión de mantenerse en los estudios depende, adicionalmente, de factores ajenos a la universidad (académicos, personales, sicosociales). Cada uno de estos enfoques parece ofrecer explicaciones complementarias de los motivos por los cuales un estudiante decide abandonar o no una institución universitaria.
Sobre esta base teórica, algunos de los autores que han reconocido la importancia de analizar empíricamente estos problemas han sido Porto et al. (2001), Cornwell (2002), Cameron y Taber (2001), Cameron y Heckman (1998), Booth y Satchell (1995), Häkkinen y Uusitalo (2003). Sin embargo, estos estudios han abordado el problema desde un marco estático, por lo que no se captura la evolución de estos fenómenos a través del tiempo. Por el contrario, estudios como los de Alemany (1990), Willett y Singer (1991), DesJardins et al. (2001, 2002), Giovagnoli (2002), entre otros, superan la limitación anterior pero han tratado de explicar la deserción y graduación a partir sólo de algunos de los factores que teóricamente han sido propuestos.
La aplicación de la metodología de modelos de duración al problema de los tiempos de deserción y graduación permite hacer un seguimiento de los estudiantes desde el inicio de sus estudios hasta que se presente alguno de los posibles eventos (deserción o graduación) y relacionarlo con el conjunto completo de factores que posiblemente pueden influenciar los tiempos de permanencia en la universidad. Una de las principales ventajas de esta metodología es que ofrece al investigador un conocimiento detallado sobre la dinámica del fenómeno en estudio, además captura el efecto de variables que cambian en el tiempo y permite la posibilidad de tener en cuenta la existencia de observaciones censuradas y empatadas.
En este sentido, se aplican los modelos de regresión de riesgo proporcional de Prentice y Gloeckler (1978) y Meyer (1990), a los tiempos de deserción y graduación de la cohorte del segundo semestre de 1996 en 11 programas de pregrado, pertenecientes a las facultades de Ingeniería (ocho programas) y Ciencias Económicas (tres programas) de la Universidad de Antioquia. Con esta metodología se busca determinar el impacto que pueden tener los factores individuales, socioeconómicos, académicos e institucionales sobre el riesgo condicional de ambos eventos en el tiempo y, además, que estos resultados contribuyan al continuo proceso de evaluación del sistema de educación superior y a la formulación de reformas educativas efectivas y eficientes en la disminución de las tasas de deserción y aumento en las de graduación.
De acuerdo con lo anterior, el texto contiene cuatro secciones. En la primera, se presentan brevemente los modelos de duración para datos agrupados o de tiempo discreto; en la segunda, se describe la información utilizada; en la tercera, se presentan los resultados obtenidos en las estimaciones y, por último, se ofrecen algunas conclusiones y recomendaciones.
I. Modelos de duración para datos agrupados
En general, los modelos de duración, también conocidos como modelos de supervivencia, se han constituido en la herramienta más popular para estudiar la relación entre los tiempos de ocurrencia de un evento y sus variables predictoras. En particular, estos modelos no sólo responden a la ocurrencia o no de un evento, sino que también permiten determinar la influencia de las variables predictoras sobre el riesgo del mismo (Singer y Willett, 1993).4
La popularidad de estos modelos, en especial el de riesgo proporcional de Cox (1972), radica en que además de responder a los interrogantes antes descritos, incorpora características que a menudo se presentan en los datos de duración, tales como la presencia de variables explicativas tiempo variantes, el censuramiento en las observaciones5 y la posibilidad de empates de los tiempos de duración.
La consecuencia de no tratar adecuadamente la presencia de observaciones censuradas genera dificultades en la estimación y en la inferencia sobre los parámetros estimados, debido a que estas proveen información incompleta sobre la ocurrencia del evento, alterando la función de verosimilitud y las propiedades de los estimadores. Igualmente, la consecuencia del desconocimiento de la naturaleza agrupada (discreta) de los tiempos de duración rinde estimadores inconsistentes con sesgo asintótico creciente a medida que el número de empates aumenta (Prentice y Gloeckler, 1978). No obstante, si existen relativamente pocos empates, es apropiado emplear un modelo en tiempo continuo haciendo algunas modificaciones a la función de verosimilitud (Cox, 1972). Si, por el contrario, existen muchos empates, entonces se debe proceder con un modelo en tiempo discreto o agrupado (Cox, 1972 y Prentice y Gloeckler, 1978). Para los fenómenos que aquí se analizan, la frecuencia de empates en los tiempos de deserción y graduación es alta debido a que su registro se lleva acabo en intervalos de tiempo semestral.
A. Modelo de heterogeneidad
Prentice y Gloeckler (1978), basados en el modelo de regresión semiparamétrico de riesgo proporcional en tiempo continuo de Cox (1972, 1975), derivan una versión para tiempos de duración discretos, con el objetivo de obtener estimadores computacionalmente factibles, tanto de la función de riesgo como de la función de supervivencia asociada.6 La función de riesgo en el momento t propuesta por Cox es
h(t|xi(t))= limΔ→0 Prob(t≤T + Δt,| T≥ t, xi(t)) ÷ Δt =h0(t) exp(xi(t)´β) (1)
donde t∈T, siendo T una variable aleatoria no negativa, la cual representa el tiempo de vida de las observaciones de una población, xi(t) es un vector de regresión asociado con la i-ésima observación que resume la heterogeneidad observada en el instante t, β es el correspondiente vector de parámetros desconocidos y h0(t) 0 es la función (arbitraria) de riesgo base en el momento t, la cual representa el riesgo común a todos las observaciones cuando xi(t) = 0. Una de las características más importantes del modelo de Cox es que la estimación del vector de parámetros, β, no requiere de una especificación sobre la función de riesgo base. Sin embargo, cuando el supuesto de riesgo proporcional es violado los estimadores son sesgados e ineficientes (Box-Steffensmeier y Zorn, 2001).
Suponiendo que existen i = 1,...,n observaciones en t = 0 y cada una es seguida hasta que se presente el evento de interés o sea censurada, que el registro de los tiempos de duración continuos de cada observación solo se lleva acabo en intervalos de tiempo discretos y disjuntos, ti∈ Aj = [aj-1, aj], j = 1,...,k con a0 = 0, ak = ∞, y permitiendo que las covariables sean tiempo dependientes entre intervalos, pero fijas dentro de los mismos (es decir, x = xi(t) dentro del intervalo Aj), entonces la función de supervivencia bajo estos supuestos está dada por
S(t|xi(t))= exp(-  h(u|xi(t))du) = exp(-exp(xi(t)´β)
h(u|xi(t))du) = exp(-exp(xi(t)´β)  h0(u)du) = exp(-exp(xi(t)´β + γj)) (2)
h0(u)du) = exp(-exp(xi(t)´β + γj)) (2)
donde γj = log(  h0(u)du) para j = 1,..., k representa el logaritmo de la función de riesgo base acumulada (o función de riesgo base integrada) entre aj-1 y aj.
h0(u)du) para j = 1,..., k representa el logaritmo de la función de riesgo base acumulada (o función de riesgo base integrada) entre aj-1 y aj.
Expresando la probabilidad de observar el tiempo de duración en tj como
Pr[Ti=t]=[1-S(j|x(tj))] S(r|x(tj)) (3)
S(r|x(tj)) (3)
y dado que la función de verosimilitud es la productoria de (3) para toda la muestra de observaciones, además definiendo un indicador de censuramiento, δi, tal que δi = 0 si la i-ésima observación es censurada y δi = 1 en otro caso, entonces se tiene que
L(β,γ)= {[1-exp(-exp(xi(ti)´β + γti))]δi
{[1-exp(-exp(xi(ti)´β + γti))]δi  exp(-exp(xi(j)´β + γj)]}
exp(-exp(xi(j)´β + γj)]}
donde la correspondiente logL(ß,γ) es
logL(β,γ)=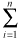 {δi log[1-exp(-exp(xi(ti)´β + γti))] -
{δi log[1-exp(-exp(xi(ti)´β + γti))] -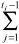 exp(xi(j)´β + γj)} (4)
exp(xi(j)´β + γj)} (4)
donde γ = [γ0,...,γk-1]´.
B. Modelo con heterogeneidad no observable
En algunas aplicaciones es razonable asumir que no se pueden observar todos los determinantes del riesgo de ocurrencia de un evento. Una de las principales ventajas del enfoque anterior es que, a parte de evitar la inconsistencia causada por la mala especificación de la función de riesgo base, la heterogeneidad de las observaciones no capturada en xi(t) (o debida a errores de medición en los datos) es fácil de incorporar (Meyer, 1990 y 1995).
Con el fin de capturar dicha heterogeneidad, Meyer (1990) asume que los atributos no observables de un individuo se pueden incorporar de manera multiplicativa en la función de riesgo a partir de una variable aleatoria εi, de forma tal que
h(t|xi(t),εi)= εi h0(t)´β) (5)
donde µ"i es una variable aleatoria con función de distribución Gamma con media uno y varianza σ2 e independiente de xi(t). Meyer (1990) adopta esta función de distribución debido a que ofrece una forma analítica cerrada de la función de verosimilitud, evitando de este modo problemas de integración numérica; sin embargo, otro tipo de funciones apropiadas pueden emplearse, por ejemplo la distribución Gaussiana Inversa7. La correspondiente función de riesgo en tiempo discreto está dada por
h(t|xi(t),εi)= {1-exp[-exp(xi(t)´β + γj + log(εi)]} (6)
y su función log-verosímil es8
logL(β,γ,σ2)= 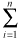 log{[1+ σ2
log{[1+ σ2  exp(xi(t)´β + γj)]-σ-2 -εi[1+ σ2
exp(xi(t)´β + γj)]-σ-2 -εi[1+ σ2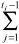 exp(xi(t)´β + γj)]-σ-2}=
exp(xi(t)´β + γj)]-σ-2}= 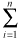 log{[1+ σ2
log{[1+ σ2 hi(t)]-σ-2 -δi[1+ σ2
hi(t)]-σ-2 -δi[1+ σ2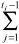 hi(t)]-σ-2} (7)
hi(t)]-σ-2} (7)
donde hi(t) = exp[xi(t)´β + γt].
Es importante mencionar que cuando σ2→0el modelo de Prentice y Gloeckler resulta como un caso límite (Jenkins, 1995b) y, además, cuando la función de riesgo base es estimada no paramétricamente, la escogencia de la distribución de la heterogeneidad no es de importancia (Meyer, 1990).
II. Datos
Para este estudio se utilizó información correspondiente a la segunda cohorte de 1996 de las Facultades de Ingeniería y Ciencias Económicas de la Universidad de Antioquia, seguida a través de 14 semestres, es decir, entre 1996" II y 2003" I.9 La fuentes de la información empleadas fueron el Sistema de Información se Matrícula y Registro " MARES" , el Módulo de Inscripción y Selección Sistemática " MOISÉS" . Además, realizó una encuesta para obtener información no incluida en los sistemas de información de la Universidad.
La cohorte está conformada por 624 alumnos, donde 454 (72,76%) pertenecen a la Facultad de Ingeniería y 170 (27,24%) a la Facultad de Ciencias Económicas, de los cuales el 24,04% continúan activos en algún programa dentro de la universidad, el 21,79% son graduados, el 51,12% son desertores y el 3,04% restante está fuera de la Universidad por bajo rendimiento académico. En el análisis no se incluyeron los desertores precoces ni las personas que salieron por bajo rendimiento,10 por lo que el número de estudiantes considerados en la muestra, aquellos para los cuales se logró conseguir información completa, es de 348, de los cuales 248 pertenecen a la Facultad de Ingeniería y 100 a la Facultad de Ciencias Económicas distribuidos finalmente así: 43% son desertores, el 34% son graduados.
De otra parte, las variables consideradas en el estudio están clasificadas de acuerdo con los diferentes enfoques teóricos que se han desarrollado en torno al problema de la deserción y graduación estudiantil y responden a los cuatro conjuntos de factores que pueden determinar la decisión de desertar o graduarse: institucionales, socioeconómicos, académicos e individuales.11 Como ejercicio previo a la estimación de los modelos y con el fin de comparar los tiempos de supervivencia de los estudiantes en cada una de las facultades, sin tener en cuenta aún el impacto de las covariables, se estimaron las funciones de supervivencia a partir del estimador no paramétrico de Kaplan-Meier tomando la información completa para la cohorte (encuestados y no encuestados).12 El estimador de Kaplan-Meier está definido como 
donde nj = nj-1- dj-1- cj- 1 para j=1,...,k; con nj definido como el número de individuos que no presentan el evento y no son censurados en tj, dj- 1 es el número de individuos que presentan el evento en tj- 1 y cj- 1 representa el número de individuos censurados en tj- 1. Los resultados de las estimaciones se reportan en el Anexo en la tabla A2.
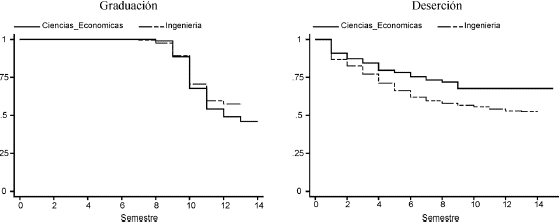
El gráfico 1 indica que las tasas de supervivencia para el evento de graduación son más altas en la facultad de Ingeniería y menores para el caso de deserción, es decir, los estudiantes de ingeniería se demoran más en graduarse y la deserción es mayor. Lo contrario ocurre en la facultad de Ciencias Económicas. Este resultado también es hallado por Häkkinen y Uusitalo (2003). El tiempo medio de graduación para las facultades de Ingeniería y Ciencias Económicas es de 12,50 y 12,31 semestres, respectivamente, por lo tanto los estudiantes se tardan aproximadamente 6,5 años; año y medio más que el tiempo teórico de graduación (cinco años).
Fuente: Cálculos propios.
Gráfico 1. Estimación no paramétrica de Kaplan" Meier de la función de supervivencia para las facultades de Ingeniería y Ciencias Económicas
III. Resultados
En las tablas 1 y 2 se presentan los resultados de la estimación de los modelos de duración de riesgo proporcional en tiempo discreto de Prentice-Gloeckler (1978) y Meyer (1990) para cada una de las facultades y cada uno de los eventos, deserción y graduación; en cada caso se consideraron como censurados los estudiantes activos y los graduados, y activos y desertores, respectivamente. Cuando el signo del coeficiente es positivo (negativo) significa que la variable asociada a éste, controlando para las demás variables, influye positivamente (negativamente) sobre el riesgo de desertar o de graduarse, según sea el caso, mientras que los coeficientes expresados en la forma de riesgo relativo, exp(β), indican cuántas veces crece (decrece) el riesgo ante un aumento en una unidad de la variable regresora. Para el caso de variables categóricas (variables en las cuales diferentes valores representan la afiliación a diferentes grupos, por ejemplo, el estrato), la interpretación será qué tan riesgoso es el grupo de estudiantes con respecto a la categoría base, controlando, igualmente, para las demás variables. De otra parte, los criterios de selección de variables significativas en los modelos fueron: un estadístico z en valor absoluto mayor que uno y que el signo esperado del coeficiente asociado fuera correcto.
La estimación de la varianza de la distribución Gamma sugiere, en ambos casos, que la heterogeneidad no observable del modelo de Meyer (1990) no es estadísticamente significativa, lo cual indica que el modelo de Prentice-Gloeckler (1978) parece ajustar mejor los datos. La prueba de razón de verosimilitud para contrastar el modelo 1 contra el modelo 2 también sugiere la misma conclusión; por tanto, el conjunto de variables incluidas en el modelo de Prentice-Gloeckler (1978) parece captar adecuadamente las diferencias entre los estudiantes. Este resultado arroja evidencia a favor de la inclusión de los cuatro conjuntos de factores: individuales, académicos, socioeconómicos e institucionales como determinantes tanto de la deserción como de la graduación estudiantil, ya que las variables incluidas en cada uno de éstos parecen explicar fundamentalmente las diferencias entre los estudiantes.
A. Deserción
Los resultados para el primer grupo de variables, las cuales tienen que ver con las características personales de los estudiantes, muestran que la edad de inicio de los alumnos parece incidir positivamente en el riesgo de desertar, aunque éste decrece marginalmente con el aumento de la misma. Así mismo, las personas casadas parecen tener un mayor riesgo de desertar, posiblemente debido a la menor disponibilidad de tiempo para dedicarse al estudio. Igualmente, las personas de género masculino parecen tener un mayor riesgo de desertar, estimándose que el riesgo de abandono para los hombres es 5,77 y 4,30 veces mayor que el de las mujeres en cada una de las facultades, Ingeniería y Ciencias Económicas, respectivamente. En el caso particular de la facultad de Ingeniería, residir en el área metropolitana del Valle de Aburrá, en comparación con las personas provenientes de otras regiones, parece disminuir el riesgo de desertar, posiblemente debido a que las personas que llegan de otras localidades incurren en costos que pueden considerarse como hundidos y que en muchos casos son difíciles de sostener por el tiempo de duración del programa. En consecuencia, esta variable puede considerarse como clave a la hora de diseñar políticas de retención estudiantil.
Dentro del conjunto de variables académicas, en las dos facultades, las que parecen ser importantes en la explicación del riesgo de deserción son: el desempeño académico en la universidad, la cual se capturó a través del número de créditos cursados y reprobados por el estudiante cada semestre. Los resultados muestran que a mayor número de créditos cursados, menor es el riesgo de desertar, mientras a mayor número de créditos reprobados, es decir a mayor repitencia, mayor es el riesgo. Así mismo, el grado de satisfacción del estudiante con el programa parece ser una variable que incide directamente en el riesgo de desertar, al encontrarse que aquellos estudiantes con un nivel de satisfacción alto o medio tienen menor riesgo de desertar en comparación con quienes tienen un bajo grado de satisfacción.13 Los resultados para la Facultad de Ciencias Económicas muestran que haber ingresado por segunda opción y no haber hecho cambio de programa aumenta en 12,23 y 46,01 veces el riesgo de deserción, respectivamente. Sin embargo, en el caso de la facultad de Ingeniería el efecto para la variable de cambio de programa es el opuesto, lo cual puede ser reflejo de la afinidad en el ciclo básico de materias entre los programas ofrecidos por esta facultad.
Específicamente, en la Facultad de Ingeniería variables como el tipo de colegio y la experiencia académica anterior, al parecer, también explican el riesgo de deserción. En el primer caso, aquellos alumnos egresados de colegios privados presentan 2,7 veces más riesgo de desertar que los provenientes de colegios públicos. En cuanto a la experiencia académica, se halló que los estudiantes que desertaron anteriormente de otra universidad tienen mayor riesgo de desertar en comparación con aquellos alumnos que ingresan por primera vez a la universidad. Por el contrario, los estudiantes que cursan simultáneamente otra carrera en otra universidad tienen 2,55 veces más riesgo de desertar en comparación con aquellos que no contaban con ningún tipo de experiencia académica. En el caso de la facultad de Ciencias Económicas los estudiantes que no tuvieron ningún tipo de orientación profesional, previo ingreso a la universidad, parecen tener 4,86 veces mayor riesgo de desertar con respecto a quienes sí la tuvieron. Como era de esperarse, una menor demora en el ingreso a la Universidad parece influir negativamente en el riesgo de desertar y éste aumenta marginalmente con el aumento del tiempo de retraso.14
En términos socioeconómicos, las personas de estrato alto y medio tienen menor riesgo de desertar en comparación con las de estrato bajo.15 Las exenciones económicas aparecen como un instrumento de política muy importante en este contexto, ya que aquellos estudiantes que tuvieron algún tipo de exención económica presentan, al parecer, menor riesgo de desertar. Los periodos de crisis económica afectan negativamente la permanencia de los estudiantes en la universidad, al ser el riesgo de deserción 1,56 veces mayor que en períodos de no crisis. Al parecer los estudiantes que dependen económicamente de sí mismos tienen un mayor riesgo de desertar. Ahora, haber trabajado en el último año de permanencia en la universidad no parece aumentar el riesgo, por lo que una combinación de las responsabilidades académicas con las laborales puede no ser desfavorable para dichos estudiantes. Igualmente, las personas que tienen algún tipo de responsabilidad económica con al menos una persona, diferente de sí mismo, tienen menor riesgo de desertar, posiblemente porque valoran más poseer un título profesional dado que éste significaría una oportunidad de mejores condiciones económicas futuras.16
Tabla 1. Estimación del modelo de riesgo proporcional para la deserción estudiantil

Fuente: cálculos propios.
En cuanto a las características educativas de los padres, para el caso de la Facultad de Ciencias Económicas, se encontró que aquellos alumnos cuyos padres tiene un nivel de educación alto (bachillerato completo, técnicos y universidad completa), al parecer, poseen un riesgo menor de desertar con respecto a los que tienen padres con niveles educativos bajos.17 Este resultado está de acuerdo con la literatura y con hallazgos de trabajo anteriores (Giovagnoli, 2002; Castaño et al., 2004). Sin embargo, al parecer, las características del programa y de la universidad, unidas a la capacidad económica de padres educados, pueden influir de manera más directa en la decisión de abandono del estudiante.
Por último, la adaptación del estudiante al ambiente universitario surge como determinante importante en la decisión de desertar. Así, mantener una buena relación con los profesores parece disminuir el riesgo de deserción mientras, por el contrario, una muy buena relación social con los compañeros, al parecer, lo aumenta. Este resultado puede estar reflejando lo que se conoce como efecto de pares, el cual tiene que ver con el hecho de que el comportamiento de los jóvenes se encuentra influenciado por el comportamiento de aquellos con quienes socializa, el cual puede determinar por ejemplo situaciones de bajo rendimiento académico y deserción.18 Por tanto, la ausencia de objetivos claros por parte de los estudiantes puede llevar a situaciones académicas que propicien el abandono de los estudios. La inestabilidad en el ritmo académico y el nivel de exigencia de la universidad no parecen incidir en el riesgo de desertar, lo cual indica que las personas perciben claramente las señales de calidad enviadas por la institución en cuanto al nivel de exigencia al que son expuestos los estudiantes y las características institucionales propias de una universidad de carácter público.
B. Graduación
A diferencia del caso de deserción, los resultados encontrados para las dos facultades muestran que la única característica personal que parece incidir en la finalización de un programa académico, dado el tiempo que lleva el alumno estudiando, es el estado civil, en tanto que los estudiantes casados tienen, al parecer, 0,36 veces menor riesgo de obtener el título profesional. Como era de esperarse, dentro del conjunto de variables académicas, el desempeño académico del estudiante juega un papel muy importante en la probabilidad de graduarse; así, un mayor número de créditos cursados y reprobados (repitencia) influye negativamente en la posibilidad de graduación. Este resultado parece indicar que tomar un número de créditos superior al preestablecido para cada semestre no siempre favorece la probabilidad de graduación. Así mismo, una mayor demora en el ingreso a la universidad parece influir negativamente en el riesgo de graduación, evidenciándose que la falta de continuidad en el proceso educativo afecta de manera determinante los objetivos de los estudiantes.
La experiencia académica anterior al parecer explica el chance condicional de graduación del estudiante. Las personas que ya contaban con un título universitario o que habían abandonado previamente sus estudios superiores tienen 1,8 veces más riesgo de graduarse en comparación con aquellas que ingresaron a la universidad por primera vez. En contraste, las personas que adicionalmente cursan otra carrera en otra universidad tienen 0,45 veces menor chance de graduarse en comparación con aquellos que no cuentan con ningún tipo de experiencia previa. En el caso de la Facultad de Ciencias Económicas, el grado de satisfacción del estudiante con el programa parece ser una variable que incide directamente en el chance de graduación; al encontrarse que aquellos estudiantes con un nivel de satisfacción bajo o medio tienen menor chance de graduación, en comparación con quienes tienen un alto grado de satisfacción. Adicionalmente, en el caso de la Facultad de Ingeniería, los programas de semillero parecen favorecer la finalización exitosa de un programa académico; así, una persona que no haya hecho parte de un programa de semillero tiene 0,58 veces menor chance de finalizar el programa con respecto a quien sí hizo parte de éstos.19
En cuanto a las variables socioeconómicas, se encontró que las personas de estrato bajo y medio tienen menor chance de graduación, en comparación con las de estrato alto. Las exenciones económicas aparecen nuevamente como importantes, influyendo positivamente en la probabilidad de graduación. Las personas que tienen algún tipo de responsabilidad económica con al menos una persona, diferente de sí mismo, parecen tener un menor riesgo de culminar exitosamente los estudios, ya que pese a que un título profesional significaría una oportunidad de mejores condiciones económicas, las responsabilidades laborales pueden afectar negativamente el desempeño del estudiante y, por tanto, retrasar su culminación. Sin embargo, trabajar en el último año de permanencia en la universidad parece influir positivamente en el riesgo de graduación.
Nuevamente, se encuentran resultados opuestos entre las dos facultades en cuanto al nivel educativo alcanzado por los padres. Para el caso de la Facultad de Ciencias Económicas, un estudiante para el cual el máximo nivel educativo entre sus padres sea bajo o medio tiene una probabilidad de graduación 0,40 y 0,37 veces menor con respecto a un estudiante con alguno de sus padres con nivel alto. En la Facultad de Ingeniería, ocurre lo contrario, teniendo un estudiante para el cual el máximo nivel educativo entre sus padres sea alto o medio, menor probabilidad de graduarse. Este resultado parece confirmar los hallazgos para deserción y, por tanto, corroborar la hipótesis de que las características del programa y de la universidad, unido a la capacidad económica de padres educados, pueden influir de manera decisiva en la permanencia del estudiante en la institución.
Las condiciones académicas de la institución parecen tener una influencia significativa sobre la probabilidad de éxito del estudiante. Así, tanto una buena carga como un buen ritmo académico parecen favorecer la probabilidad de graduación del estudiante. En el caso particular de la Facultad de Ingeniería, una buena relación con los profesores también parece favorecer la probabilidad de graduación. En consecuencia, la formación de expectativas claras sobre las condiciones de vida académica y estudiantil en el medio universitario, la rápida adaptación por parte del estudiante al ambiente institucional, la compatibilidad entre los intereses o preferencias del estudiante y las exigencias de la vida académica favorecen la culminación exitosa del estudiante.
Por último, nótese que las variables socioeconómicas no parecen influir en la probabilidad de graduación en el caso de la Facultad de Ciencias Económicas, con excepción del trabajo del estudiante en el último año, el cual influye, al parecer, negativamente en el riesgo de graduación. Además, los períodos de crisis económica no parecen afectar la probabilidad de graduación de los estudiantes, tampoco la mayoría de variables personales, tales como ingresar a la universidad con mayor edad, residir en el área metropolitana o residir con la familia.
Tabla 2. Estimación del modelo de riesgo proporcional para la graduación estudiantil
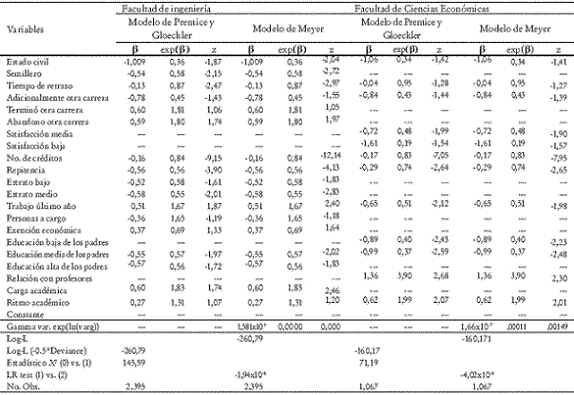
Fuente: cálculos propios.
IV. Pruebas de diagnóstico
Para la validación de los modelos se realizaron pruebas de diagnóstico referentes al ajuste del modelo, los cuales incluyen la presencia de observaciones influenciales que pudieran distorsionar los efectos de las variables explicativas, la significancia de las variables, la presencia de multicolinealidad y la confirmación del supuesto de proporcionalidad.20
En primer lugar, con el fin de evaluar la robustez del ajuste del modelo y para evitar errores de mala especificación, se usó el método leverage para determinar si existen observaciones que tienen una influencia desproporcionada sobre la estimación de los parámetros. Este análisis consiste en comparar el vector de parámetros estimados obtenido con la muestra completa, , con el vector de parámetros estimados eliminando la influencia de la i-ésima observación,
, con el vector de parámetros estimados eliminando la influencia de la i-ésima observación,  i. Si
i. Si  -
- i, la i-ésima observación tiene poca influencia sobre el ajuste del modelo. ΔV(
i, la i-ésima observación tiene poca influencia sobre el ajuste del modelo. ΔV( ), donde es la matriz de residuales score eficientes y V(
), donde es la matriz de residuales score eficientes y V( ) es la matriz de varianza y covarianza de . Los resultados indican tanto para el caso de graduación como de deserción la existencia de dos datos influenciales correspondientes a los estudiantes 96 y 186 en los modelos de ingeniería y uno correspondiente al estudiante 235 en los modelos de ciencias económicas.
) es la matriz de varianza y covarianza de . Los resultados indican tanto para el caso de graduación como de deserción la existencia de dos datos influenciales correspondientes a los estudiantes 96 y 186 en los modelos de ingeniería y uno correspondiente al estudiante 235 en los modelos de ciencias económicas.
Los resultados para la prueba conjunta del supuesto de riesgo proporcional se presentan en la tabla 3. El contraste para cada uno de los modelos descritos anteriormente muestra que no es posible rechazar la hipótesis nula de riesgo proporcional.
Tabla 3. Prueba conjunta del supuesto de proporcionalidad

Fuente: cálculos propios.
V. Conclusiones y recomendaciones
El rechazo del modelo de Meyer (1990), el cual considera el supuesto de heterogeneidad no observada, confirma la evidencia encontrada en trabajos anteriores a favor de la inclusión de los cuatro conjuntos de factores: individuales, académicos, socioeconómicos e institucionales como determinantes tanto de la deserción como de la graduación estudiantil. Esto indica que considerar factores aislados o la combinación de algunos de ellos no permite obtener conclusiones robustas sobre los determinantes de estos eventos. En consecuencia, es claro que para lograr un mejor entendimiento de las decisiones que toman los estudiantes durante su ciclo académico es necesario combinar más que enfrentar los modelos teóricos que buscan explicar los motivos por los cuales los estudiantes deciden abandonar o mantenerse en una institución de educación superior.
Los resultados del modelo permiten diseñar políticas orientadas a la retención estudiantil, sin embargo, las estrategias de intervención deben centrarse en aquellas variables que pueden ser manipuladas y que aparecen como fuertes determinantes de las decisiones que el estudiante puede tomar durante su permanencia en la universidad. De acuerdo con lo anterior, y según los resultados para el conjunto de variables incluidas en el modelo algunas estrategias orientadas a atacar el problema de la deserción pueden ser: permitir la libre migración de los estudiantes entre programas académicos, regulando de una manera más eficaz el ingreso de estudiantes que cursan simultáneamente carreras en otras universidades; brindar mejor y mayor información acerca de los programas ofrecidos por la universidad, haciendo especial énfasis en las diferencias de enfoques de estos con respecto a los existentes en otras universidades; crear acciones de ayuda para los estudiantes de estrato bajo en periodos de crisis económica y también para aquellos que provienen de localidades diferentes del área metropolitana de Medellín.
Así mismo, con el fin de motivar la graduación de los estudiantes en el tiempo teórico de los programas académicos, es importante que las instituciones de educación superior, en particular las públicas, emprendan campañas pedagógicas sobre la importancia de terminar los estudios en el tiempo teórico haciendo énfasis en los costos que representa tanto para los estudiantes y sus familias como para las instituciones y la sociedad el retrazo en la obtención de un título profesional. Adicionalmente, otra política orientada al favorecimiento de la finalización exitosa de los estudios podría ser la mayor promoción de los programas de semillero, los cuales unidos a una apropiada orientación profesional pueden promover tanto la graduación como la retención estudiantil. Por último, es importante aclarar que aunque la generalización de estos resultados a otros programas e instituciones es posible; ésta debe hacerse teniendo en cuenta tanto las particularidades de cada programa académico como las características propias de cada institución.
Anexo
Tabla A1. Descripción detallada de las variables consideradas en el modelo


Tabla A2. Universidad de Antioquia: estimación no paramétrica de Kaplan" Meier de la función de supervivencia para las facultades de Ingeniería y Ciencias Económicas
Notas

1 Al respecto véase Psacharopoulos (1985), Psacharopoulos y Patrinos (2002).
2 Esto es particularmente evidente en el sector privado, donde las matrículas son parte sustancial de los ingresos institucionales, pero no lo es menos en el sector público debido a sus limitaciones presupuestales.
3 Véase al respecto Schultz, (1961), Nelson y Phelps (1966), Romer (1990), Benhabib y Spiegel (1994), Temple (1999), y Krueger y Lindahl (2000).
4 Kiefer (1988) ofrece una completa lista sobre las áreas de aplicación de los modelos de duración.
5 Una observación está censurada cuando ésta no experimenta el evento de interés antes de que el periodo de recolección de la información finalice. Esta definición obedece al censuramiento a derecha, el cual es muy común en muchas aplicaciones. Para la descripción de otros tipos de censuramiento (por ejemplo, el censuramiento a izquierda y el censuramiento por intervalos), véase por ejemplo Lawless (1982), Kiefer (1988), Lancaster (1992), y Hosmer y Lemeshow (1999).
6 Cox (1972) generaliza su propuesta de la función de riesgo para un número pequeño de empates.
7 Campolieti (2003) propone un enfoque alternativo asumiendo que la distribución de la heterogeneidad no observable es no paramétrica y fijando una especificación flexible de la función de riesgo base con el fin de superar los problemas numéricos que se han encontrado en algunas aplicaciones.
8 Véase Meyer (1990 y 1995) para su derivación.
9 Estas facultades están compuestas por los siguientes programas académicos: Ingeniería de Sistemas, Ingeniería Eléctrica, Ingeniería Electrónica, Ingeniería Industrial, Ingeniería Mecánica, Ingeniería Química, Ingeniería Sanitaria en la Facultad de Ingeniería ; y en el caso de la Facultad de Ciencias Económicas: Contaduría, Economía y Administración de Empresas.
10 Un desertor precoz es aquel estudiante que habiendo sido aceptado por la universidad no se matricula para el primer semestre académico. Para una descripción detallada de los diferentes tipos de deserción véase Castaño, et al. (2004).
11 Véase al respecto Castaño et al. (2004); para una descripción detallada de cada una de las variables incluidas en el modelo véase en el Anexo, tabla A1.
12 Los estimadores no paramétricos de la función de supervivencia como el de Kaplan-Meier tienen en cuenta las características propias de los datos de duración debido a que éstos no hacen supuestos sobre la distribución de los tiempos de duración.
13 En el caso de la facultad de ingeniería se redujeron las categorías de satisfacción alta, media y baja a alta y baja al encontrarse, en estimaciones preliminares, que estos coeficientes no eran significativamente diferentes con un nivel de confianza del 5%.
14 El coeficiente asociado a la variable tiempo de espera fue igual a -0,35, con exp(β) igual a 0,28 y un valor t de 0,70 en la estimación del modelo de Prentice y Gloeckler.
15 Para la cohorte 1996-II en la Facultad de Ciencias Económicas no inició ninguna persona de estrato alto por lo que en este caso la comparación se realizó entre personas de estrato 3 y 4, considerándose este como alto, y personas de estrato 1 y 2.
16 Esta situación es claramente diferente a la de una persona casada ya que está no tiene responsabilidades familiares. En estimaciones preliminares se realizaron pruebas discriminando las personas a cargo entre hijos y otras personas. Sin embargo, la variable no resultó estadísticamente significativa aunque presentaba el signo esperado. Es importante mencionar que aunque estas últimas variables solo aparecen como significativas para el caso de la facultad de Ingeniería o Economía los signos de las mismas se mantienen en ambas facultades, lo cual confirma la dirección del efecto sobre el riesgo de deserción.
17 Debido a la similitud en los coeficientes estimados para la educación del padre y de la madre se definió una nueva variable que responde al máximo nivel educativo entre estos, definiéndose similarmente tres categorías: alta, media y baja. Sin embargo, resultados preliminares mostraron que los coeficientes asociadas a la educación media y alta no eran significativamente diferentes por lo que finalmente se dejaron dos categorías: alta y baja.
18 Al respecto véase: Sacerdote, B., (2001), Gaviria, A and Steven R. (2001), y McEwan, Patrick J., (2003).
19 Los programas de semillero buscan introducir a los estudiantes de educación secundaria en el ambiente universitario y despertar el interés por el estudio de una determinada ciencia. Así mismo, buscan desarrollar habilidades de pensamiento y por consiguiente de procesos de análisis, síntesis, evaluación y solución de problemas.
20 Veáse Cleves, Gould y Gutiérrez (2002).
Bibliografía
1. Ahlburg, D., McCall, B. y Na, I. (2002). " Time to Drop out from College: A Hazard Model with Endogenous Waiting", Working Paper 01, Industrial Relations Center, University of Minnesota. [ Links ]
2. Alemany, R. (1990). " Modelación de la duración de estudios universitarios: una aplicación a la Universidad de Barcelona,
3. Arulampalam, W., Naylor, R., y Smith, J. (2003). " A Hazard Model of the Probability of Medical School Dropout in the United Kingdom , University of Warwick. [ Links ]
4. Bean, J. P. (1980). "Student Attrition, Intensions and Confidence , Research in Higher Educationation, Vol. 17, 291-320. [ Links ]
5. Benhaabib, J. y Spiegel, M. (1994). " The Role of Human Capital in Economic Development Evidence from Aggregate Cross-country Data , Journal of Monetary Economics, 34, 143-173. [ Links ]
6. Booth, A. y Satchell, S. (1995)." The Hazards of Doing a PhD: An Analysis of Completion and Withdrawal Rates of British PhD Students in the 1980s" , Journal of the Royal Statistical Society, A158, 297-318. [ Links ]
7. Box-Steffensmeier, J. y Zorn, C. (2001). "Duration Models and Proportional Hazards in Political Science , American Journal of Political Science, 45, 972-988. [ Links ]
8. cabrera, A., Nora, A. y Castañeda, M. (1993). " Collage Persistence: Structural Equations Modeling Tests of an Integrated Models Student Retention , The Journal of Human Resources, 64, 123-139. [ Links ]
9. Cameron, S. y Taber, C. (2001). "Estimation of Education Borrowing Constraint using Returns Schooling",
10. Cameron, S. y Hheckman, J. (1998). " Life Cycle Schooling and Dynamic Selection Bias: Models and Evidence for Five Cohorts of American Males , The Journal of Political Economy, 106, 262-333. [ Links ]
11. Campolieti, M. (2003). "On the Estimation of Hazard Models with Flexible Baseline Hazards and Nonparametric Unobserved Heterogeneity , Economics Bulletin, 3, 1-10. [ Links ]
12. Card, D. (2001). " Estimating the Return to Schooling: Progress on Some Persistent Econometric Problems , Econometrica, 69, 1127-1160. [ Links ]
13. Castaño, E., Gallón, S., Ggómez, K. y Vásquez, J. (2004). "Deserción estudiantil universitaria: una aplicación de modelos de duración , Lecturas de Economía, 60, 41-65. [ Links ]
14. Cleves, M., Ggould, W. y Ggutiérrez, R. (2002). An Introduction to Survival Analysis Using Stata, Stata Press, Texas. [ Links ]
15. Cornwell, C. (2002). " The Enrollment Effects of Merit-Based Financial Aid: Evidence from Georgia" s HOPE Scholarship , University of Georgia, Department of Economics. [ Links ]
16. Cox, D. R. (1972). " Regression Models and Life Tables , Journal of the Royal Statistical Society, B34, 187-220. [ Links ]
17. Dagenais, M., Montmarquette, C. y Viennot-Briot, N. (2001). "Dropout, School Performance and Working while in School: An Econometric Model with Heterogeneous Groups" ,
18. DesJardins, S., Ahlburg, D. y McCall, B. (2001). "Simulating the Longitudinal Effects of Ghanges in Financial Aid on Student Departure from College", Journal of Human Resources, 37, 653-679. [ Links ]
19. Ensminger, M. y Slusarcick, A. (1992). " Paths to High School Graduation or Dropout: A Longitudinal Study of A First" Grade Cohort , Sociology of Education, 65, 95-113. [ Links ]
20. Fobih, D. K. (1987). "Social-Psychology Factors Associated with Dropout School in the Eastern Region of Ghana , The Journal of Negro Education, 56, 229-239. [ Links ]
21. Gaviria, A y Steven, R. (2001). School-Based Peer Effects and Juvenile Behavior , Review of Economics and Statistics, 83, 257-268. [ Links ]
22. Giovagnoli, P. (2002). " Determinantes de la deserción y graduación universitaria: una aplicación utilizando modelos de duración, Documento de Trabajo, 37, Universidad Nacional de la Plata. [ Links ]
23. Griliches, Z. (1977). "Estimating Returns to Schooling: Some Econometric Problems, Econometrica, 45, 1-22. [ Links ]
24. Häkkinen, L. y Uusitalo, R. (2003). "The Effect of a Student Aid Reformon Graduation: A Duration Analysis, Working Paper Series, No. 8, Department of Economics, Uppsala University. [ Links ]
25. Han, A. y Hausman, J. (1990). " Flexible Parametric Estimation of Duration and Competing Risk Models, Journal of Applied Econometrics, 5, 1-28. [ Links ]
26. Heckman, J. y Singer, B. (1984). "Econometric Duration Analysis", Journal of Econometrics, 24, 63-132. [ Links ]
27. Hosmer, D. y Llemeshow, S. (1999). Applied Survival Analysis: Regression Modeling of Time to Event Data, John Wiley & Sons. [ Links ]
28. Jenkins, S. P. (1995). " Easy Estimation Methods for Discrete-Time Duration Models , Oxford Bulletin of Economics and Statistics, 57, 129-138. [ Links ]
29. Kalbfleisch, J. D. y Prentice, R. L. (1973). "Marginal Likelihoods Based on Cox" s Regression and Life Model , Biometrika, 60, 267-278. [ Links ]
30. Kaplan, E. L. y Meier, P. (1958). " Nonparametric Estimation from Incomplete Observations , Journal of the American Statistical Association, 53, 457-481. [ Links ]
31. Kiefer, N. (1988). "Economic Duration Data and Hazard Functions , Journal of Economic Literature, 26, 646-679. [ Links ]
32. Krueger, A. B. y Llindahl, M. (2000). " Education for Growth: Why and for Whom?", NBER Working Paper, 7591. [ Links ]
33. Lancaster, T. (1992). The Econometric Analysis of Transition Data, Cambridge University Press. [ Links ]
34. Lawless, J. F. (1982). Statistical Models and Methods for Lifetime Data, John Wiley Sons. [ Links ]
35. McEewan, P. J. (2003). " Peer Effects on Student Achievement: Evidence from Chile , Economics of Education Review, 22, 131-41. [ Links ]
36. Meyer, B. (1990). " Unemployment Insurance and Unemployment Spells , Econometrica, 58, 757-782. [ Links ]
37. Nelson, R. y Phelps, E. (1966). " Investments in Humans, Technological Diffusion and Economic Growth , American Economic Review, 56, 69-75. [ Links ]
38. Neuman, G. (1997). " Search Models and Duration Data , in: M. H. Pesaran and P. Schmidt, eds., Handbook of Applied Econometrics, Vol. II, Blackwell, 300-351. [ Links ]
39. Porto, A. y Di Ggresia, A. (2001). "Rendimiento de estudiantes universitarios y sus determinantes , Asociación Argentina de Economía Política. [ Links ]
40. Prentice, R. y Ggloeckler, L. (1978). "Regression Analysis of Grouped Survival Data with Application to Breast Cancer Data", Biometrics, 34, 57-67. [ Links ]
41. Psacharopoulos, G. (1985). "Returns to education: A Further Update and Implications , The Journal of Human Resources, 20, 583-604. [ Links ]
42. Psacharopoulos, G. y Patrinos, H. (2002). " Returns to Investment in Education: A Further Update , Policy Research Working Paper, 2881, World Bank. [ Links ]
43. Romer, P. (1990). "Endogenous Technological Change , Journal of Political Economy, 98, S71-S102. [ Links ]
44. Sacerdote, B. (2001). Peer Effects with Random Assignment: Results for Dartmouth Roommates , Quarterly Journal of Economics, 116, 681-704. [ Links ]
45. Schultz, T. W. (1961). " Investment in Human Capital , American Economic Review, 51, 1-17. [ Links ]
46. Singer, J. D. y Willett, J. B. (1991). "Modelling the Days of Our Lives: Using Survival Analysis When Designing and Analyzing Longitudinal Studies of Duration and the Timing of Events", Psychological Bulletin, 110, 268-290. [ Links ]
47. Spady, W. (1970). " Dropout from Higher Education: An Interdisciplinary Review and Synthesis , Interchange, Vol. 1, 64-85. [ Links ]
48. Temple, J. (1999). "A Positive Effect of Human Capital on Growth , Economics Letters, 65, 131-134. [ Links ]
49. Tinto, V. (1975). " Dropout from Higher Education: A Theoretical Synthesis of Recent Research , Review of Education Research, Vol. 45, 89-125. [ Links ]
50. van den Berg, G. J. (2001). "Duration Models: Specification, Identification and Multiple Durations", in: J. J. Heckman and E. Leamer, eds., Handbook of Econometrics, Vol. 5, Amsterdam: North-Holland. [ Links ]
51. Willett, J. B. y SinNger, J. D. (1991). " From Whether to When: New Methods for Studying Student Dropout and Teacher Attrition , Review of Educational Research, 61, 407-450. [ Links ]