Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Lecturas de Economía
Print version ISSN 0120-2596
Lect. Econ. no.81 Medellín July/Dec. 2014
ARTÍCULOS
Burbujas financieras y comportamiento reciente de los mercados de acciones en América Latina
Financial bubbles and recent behaviour of the Latin American stock markets
Les bulles financières et le comportement récent des marchés boursiers en Amérique latine
Jorge Uribe*; Julián Fernández**
* Profesor del Departamento de Economía de la Universidad del Valle. Integrante del Grupo de Macroeconomía Aplicada y Economía Financiera de esa misma universidad. Jorge Mario Uribe agradece el apoyo de la Universidad del Valle y del Centro de Investigaciones y Documentación Socioeconómica (CIDSE). Las opiniones expresadas en este documento son responsabilidad de los autores y no comprometen a la Universidad del Valle. Dirección postal: Calle 13 No 100-00 Ciudad Universitaria Meléndez, Edificio 387, Departamento de Economía. Dirección electrónica: jorge.uribe@correounivalle.edu.co.
** Estudiante de la maestría en Economía Aplicada de la Universidad del Valle. Integrante del Grupo de Macroeconomía Aplicada y Economía Financiera de esa misma universidad. Dirección postal: Calle 13 No 100-00 Ciudad Universitaria Meléndez, Edificio 387, Departamento de Economía. Dirección electrónica: julian.fernandez.mejia@correounivalle.edu.co.
–Introducción. –I. Una historia de Burbujas Sincronizadas. –II. Burbujas: en el centro del debate. –III. Prueba de Signo para detectar burbujas. –IV. Resultados. –Conclusiones, recomendaciones y limitaciones del análisis. –Bibliografía. –Apéndice
Primera versión recibida el 19 de octubre de 2013; versión final aceptada el 1 de abril de 2014
RESUMEN
Con el fin de poner a prueba hipótesis recientes en la literatura económica, según las cuales la formación de burbujas periódicas y sincronizadas en los mercados globales es consecuencia de la migración recurrente de capitales de portafolio, en este trabajo se estiman los periodos de burbujas financieras en los mercados de acciones latinoamericanos de mayor tamaño relativo; asimismo, la cronología de tales burbujas se compara con la estimada para el caso estadounidense. Estas burbujas se estiman haciendo uso de un estadístico de signo, con ajuste recursivo de mediana, el cual sirve para contrastar la hipótesis de caminata aleatoria versus alternativas explosivas. Se encuentra evidencia favorable para la hipótesis de partida y se exploran posibles ampliaciones de ésta.
Palabras Clave: burbujas especulativas, caminatas aleatorias, prueba de signo, mercados accionarios de América Latina y Estados Unidos.
Clasificación JEL: G01, G14, C22, C15, C18, C58.
ABSTRACT
To contrast recent hypotheses in the economic literature stating that the formation of periodic and synchronized bubbles in global markets is a consequence of portfolio asset migrations, the financial bubbles of the Latin American stock markets with the biggest relative market size are estimated in this paper. Also, the chronology of the bubbles is compared to the one estimated for the United States. The bubbles are estimated using a sign test based on recursive median adjustment, which is used to test the null hypothesis of a random walk against the alternative of explosive processes. Empirical evidence is found that confirms the original hypothesis and allows exploring possible expansions thereof.
Keywords: Speculative bubbles, random walk, sign test, Latin American and US stock markets.
JEL Classification: G01, G14, C22, C15, C18, C58.
RÉSUMÉ
Afin de tester les hypothèses récentes dans la littérature à savoir : la formation de bulles périodiques et synchronisés dans les marchés mondiaux est due à la migration persistante des investissements de portefeuille. Nous identifions les périodes dans lesquelles l'on peut constater l'existence des bulles financières pour les plus grands pays d'Amérique latine. Nous établissons ensuite une comparaison avec l'existence des bulles financières pour le cas des États-Unis. Ces bulles sont estimées en utilisant le test de signe statistique avec ajustement récursif par la médiane, lequel sert à tester l'hypothèse de promenade aléatoire versus alternatives explosives. Les tests sont favorables à cette hypothèse et des études complémentaires sont explorées.
Mots-clés: bulles spéculatives, marchés aléatoires, test du signe, marchés boursiers en Amérique latine et aux États-Unis.
Classification JEL: G01, G14, C22, C15, C18, C58.
Introducción
Caballero, Farhi y Gourinchas (2008a) proponen una cronología intuitiva para explicar las fluctuaciones de los precios de los activos en los mercados financieros globales que se han presentado en épocas recientes. Argumentan que en esta dinámica hay burbujas especulativas presentes, las cuales surgen como producto de una demanda excesiva de títulos valores e instrumentos financieros en un mundo de oferta limitada y asimétrica de tales títulos. La idea general es que en un mundo con excesos de liquidez, originados por la prevalencia de tasas de interés bajas en Estados Unidos, los capitales de portafolio fluyen de un mercado a otro, causando la aparición de burbujas financieras de forma relativamente sincronizada alrededor del mundo.
De esta manera, las crisis registradas en los países emergentes durante la década de los noventa habrían de provocar una salida de capitales financieros, los cuales buscarían refugiarse en distintos mercados de la economía norteamericana: de acciones, hipotecario, de bonos, etc. Posteriormente, el comienzo de la crisis subprime implicaría una reversión de estos capitales, que esta vez buscarían refugio en la inversión en commodities, tales como el petróleo, la plata o el oro. El incremento relativo de los precios de los commodities habría de generar nuevos recursos para los países emergentes, en su mayoría productores de dichos bienes; estos recursos serían invertidos nuevamente en las economías desarrolladas, en particular la estadounidense, precisamente porque esos mercados (emergentes) ofrecen pocas oportunidades de inversión financiera. Lo anterior debería actuar como combustible para la generación de nuevas burbujas en la economía de Estados Unidos y, en general, en los mercados mundiales.
La hipótesis de partida del presente documento es que existen burbujas especulativas registradas en los precios de las acciones en distintas economías de Latinoamérica, y que tales burbujas presentan periodos de origen y colapso sincronizados con respecto a los de otras burbujas detectables en los mercados de acciones globales (como el de los Estados Unidos) o en los mercados de commodities (como los de petróleo u oro). Esta sincronización quiere decir que en cuanto se comienzan a ''desinflar'' unas burbujas, se comienzan a ''inflar'' las otras, y este patrón se mantiene en el tiempo recurrentemente. Para este trabajo se tomaron como muestra de estudio las últimas dos décadas de los mercados de México, Colombia, Argentina, Brasil, Perú y Chile.
La forma empírica de contrastación de la hipótesis de partida se valdrá de un test de signo con ajuste recursivo de mediana propuesto por Uribe (2013) para detectar burbujas. La prueba no es otra cosa que el estadístico de signo de So y Shin (2001), aplicado a submuestras traslapadas del periodo de estudio mediante ventanas móviles de ancho fijo. Esta prueba se considera conveniente puesto que a nivel estadístico tiene mayor potencia (asintótica local) que otras pruebas de caminatas aleatorias, como la ADF, la PP, o la KPSS, tal y como lo muestran So y Shin (2001), sobre todo cuando los datos bajo análisis presentan una fuerte heteroscedasticidad condicional y colas pesadas (exceso de curtosis); este es el caso de las series financieras con las que se trabajó. Adicionalmente, este estadístico permite el cambio de la hipótesis alternativa por el de explosividad, en lugar de estacionaridad o raíz unitaria, lo cual, como se verá más adelante, resulta conveniente para detectar burbujas positivas en el precio de los activos financieros, ya que estas burbujas se reflejan en comportamientos explosivos de los precios por periodos de tiempo acotados.
Por otra parte, como lo señala Uribe (2013), la aplicación del estadístico de forma iterativa, en submuestras de longitud fija, hace posible capturar la dinámica temporal del proceso de origen y colapso de las burbujas; esto, a su vez, permite sortear la crítica de Evans (1991) al algoritmo de Diba y Grossman (1987), al ser éste incapaz de detectar burbujas que colapsan periódicamente. De la misma forma, utilizar ventanas móviles para la selección de la muestra, en lugar de Mínimos Cuadrados Recursivos, permite crear un estadístico más sensible a la aparición y desaparición de los procesos explosivos.
Se encuentra evidencia que respalda la hipótesis de Caballero et al. (2008a) y se alzan nuevos interrogantes que pueden servir para enriquecer el debate sobre el papel de los bancos centrales de la región en términos de la prevención de este tipo de fenómenos.
El remanente de este documento explica las implicaciones teóricas del modelo de Caballero et al. (2008a) con algún grado de detalle, y se establecen así las hipótesis a contrastar. A continuación se hace un resumen de la literatura teórica y empírica sobre las burbujas especulativas. Una cuarta sección expone al detalle la metodología seguida para llevar a cabo las estimaciones aquí presentadas, y la última sección concluye.
I. Una historia de Burbujas Sincronizadas
Caballero et al. (2008a) parten de la premisa de que en la economía mundial actual, particularmente en las economías emergentes, la oferta de instrumentos financieros sólidos y líquidos es escasa. Esta escasez lleva a que se presenten flujos importantes de capital hacia los Estados Unidos y a la consecuente creación de burbujas en el precio de los activos de ese mercado, las cuales, eventualmente, colapsan.
La historia empieza en la década de los noventa cuando las crisis de los mercados emergentes, el rápido crecimiento de China y de algunas economías del este de Asia, y el incremento simultáneo del precio de algunos commodities, reorientaron los flujos de capital desde los países emergentes hacia los Estados Unidos; esto con el fin de buscar instrumentos financieros sólidos y líquidos que permitieran preservar el valor de la nueva riqueza (Caballero, Farhi y Gourinchas, 2008b).
Una consecuencia colateral de la entrada masiva de estos capitales sería la reducción de las tasas de interés de mercado en Estados Unidos y la generación de burbujas en sus mercados de valores (tanto de acciones como hipotecario).
La crisis financiera que tuvo lugar entre 2007 y 2009 exacerbó la escasez de activos financieros para la inversión, lo cual llevó a los capitales a refugiarse en la inversión en commodities como el petróleo; esto generó un flujo de petro-dólares de vuelta a Estados Unidos en busca de activos financieros sólidos. El regreso de los capitales a la economía norteamericana ayudó a mantener bajas las tasas de interés de mercado en dicha economía y aportó el combustible para la generación de nuevas burbujas.
Si bien la historia de Caballero et al. (2008a) llega hasta el año 2008, se provee una continuación de la misma basada en las hipótesis de estos autores. Los capitales de portafolio deberían haber empezado a inflar burbujas– no solo en Estados Unidos, sino posiblemente en otros mercados alrededor del mundo– después del colapso de las burbujas en los mercados de commodities, más aún en medio de la crisis europea, la cual tendría el efecto de haber resentido, todavía más, las posibilidades de inversión financiera a gran escala, disminuyendo así la oferta de papeles financieros líquidos, e induciendo una mayor escasez en la oferta de instrumentos en los cuales invertir. Estas burbujas deberían estar inflándose en el propio mercado norteamericano, o incluso en los mercados latinoamericanos en la actualidad (o en su defecto en los mercados asiáticos).
La hipótesis de Caballero et al. (2008a) tiene, en principio, manifestaciones empíricas precisas:
i. Se debería presentar un periodo de reducción en las tasas de interés de mercado de la economía estadounidense (por ejemplo las tasas de los títulos del Tesoro a 10 años) después del colapso de las burbujas generadas fuera de ese país (ya que esto conlleva una entrada de flujos de capital a la economía norteamericana), en particular durante la década de los noventa.
ii. De ser posible medir las burbujas en los mercados, éstas deberían responder a las características prescritas por el modelo, es decir, las fechas de origen de algunas de ellas deberían coincidir con las fechas de fin de las otras. Particularmente, las burbujas de los mercados emergentes, como el latinoamericano de los años noventa, deberían haber migrado a los mercados financieros estadounidenses (de acciones industriales, de acciones de empresas tecnológicas, mercado inmobiliario, etc.).
iii. Sería de esperar que las burbujas en los precios de los commodities tuvieran menor duración que aquellas en los precios de otros activos financieros en Estados Unidos puesto que se trata solo de una salvaguarda temporal que sirve como vehículo financiero, en tanto la inversión se encauza nuevamente hacia los mercados norteamericanos. De la misma forma, estas burbujas deberían aparecer aproximadamente después del estallido de la crisis subprime.
Algunas de estas implicaciones son estudiadas por Caballero et al. (2008a). Para el primer hecho descrito, el análisis gráfico de correlaciones que ellos realizan puede brindar alguna luz. No obstante, hechos como el segundo y el tercero requieren de la estimación puntual de periodos de burbuja. No basta con un análisis de la evolución de las series de precios bajo estudio en niveles. Se trata de hechos (propiedades estocásticas de las series), más que de hechos estilizados (tendencias y gráficas) según lo planteado por Hoover, Johansen y Juselius (2008).
Como se verá, el problema de la detección y medición de burbujas financieras no es fácil de resolver; por el contrario, tiene raíces profundas en la teoría económica y en la econometría teórica. Dos preguntas centrales en este campo son: ¿los precios de los activos financieros incorporan alguna vez componentes no fundamentales en su dinámica?, y si es así, ¿cómo detectar, empíricamente, periodos de sobre o subvaloración de estos activos, dado que se trata de una situación que por definición es no observable?
II. Burbujas: en el centro del debate
Hace ya más de tres décadas Tirole (1982) escribió sobre la imposibilidad de incorporar burbujas en los modelos de equilibrio general con agentes que forman sus expectativas racionalmente. Su argumento se basa en que a menos que los participantes en el mercado tengan creencias ex ante distintas sobre el valor de un activo dado, o sean capaces de utilizar el mercado correspondiente como uno de seguros, éste no permitirá la aparición de ganancias especulativas por transacciones. Por lo tanto, la especulación se apoya en el diseño de planes inconsistentes que son descartados por las Expectativas Racionales (ER).
El anterior resultado, o bien obligó a las burbujas a habitar en los terrenos del equilibrio general en los modelos de generaciones traslapadas (Tirole, 1985), en donde han estado presentes desde Samuelson (1958) y Shell (1971) resolviendo ineficiencias dinámicas en la economía encarnadas en el dinero fiduciario; o bien las obligó a buscar su camino por fuera de la hipótesis de las ER.
En este último campo no han sido pocos los avances logrados por autores como Abreu y Brunnermeier (2003), quienes demuestran que bastan unos pocos noisetraders (agentes irracionales) para que una burbuja comience y posea cierta desincronización en las estrategias de transacción de los arbitrajistas racionales para que ésta persista indefinidamente. Otros autores como Farmer (2012) incorporan en los modelos típicos nociones de sentimiento de mercado o crisis de confianza, al estilo de Shiller (2000), para explicar la aparición y la no dilución inmediata de las burbujas. Aunque estos choques de confianza son tratados como aleatorios y exógenos de los choques tecnológicos en los modelos de Equilibrio General habituales, su naturaleza es distinta a la de los segundos, ya que imponen cierta ''no racionalidad'' en los agentes de mercado.
Otros avances de la literatura han tratado de modelar explícitamente la forma en que los agentes generan sus expectativas con base en la información disponible, a través de mecanismos de aprendizaje recursivos o bayesianos, los cuales pueden dar paso a la aparición de burbujas endógenamente (Branch y Evans, 2011).
Finalmente, las burbujas también han sido abordadas como problemas de agencia en modelos de equilibrio parcial, como lo hacen Allen y Gale (2000). En estos modelos los inversionistas (agentes) en la economía tienen incentivos a decidirse por proyectos excesivamente riesgosos, dado que no prevén las consecuencias totales de sus acciones o no deben enfrentar los costos completos de las mismas. Los bancos (principal), por su parte, no tienen control sobre las decisiones de los inversionistas. Por lo tanto, el resultado de la transacción en el mercado es que los inversionistas toman riesgos excesivos, y en caso de pérdida se declaran insolventes, dejando al banco enfrentar la realización de la pérdida. Este comportamiento no es óptimo para la economía como un todo, y es el que lleva a la generación de burbujas (positivas o negativas).
A. Medición empírica
La identificación de burbujas financieras ha sido abordada por la econometría desde décadas atrás. Gurkaynak (2008) presenta una tipología de cinco categorías, útil para clasificar los distintos avances: i) pruebas de acotamiento en la varianza, ii) pruebas en dos etapas de West, iii) pruebas de cointegración, iv) pruebas de burbujas intrínsecas y v) pruebas de burbujas como variable no observable. Esta sección incluye un resumen del estudio antes citado, así como algunas extensiones a la literatura aparecidas en épocas más recientes.
i) Las pruebas de acotamiento en la varianza (Shiller, 1981; LeRoy y Porter, 1981) se basan en que, bajo el supuesto de expectativas racionales, la diferencia entre los dividendos esperados y las expectativas de los mismos es una variable aleatoria imposible de pronosticar con valor esperado cero. Lo que es lo mismo:

donde Pt* es el precio expost racional y Pt es el precio observado, r es el factor de descuento y εt es la diferencia entre los dividendos esperados y los observados. En este caso se tiene que debido a la ortogonalidad entre εt y Pt impuesta por la ER:

φ > 0, y por tanto, la varianza de los precios ex post debe ser más grande que la de los precios observados en los datos bajo la hipótesis nula de burbujas inexistentes. Encontrar indicios de que esta relación entre las varianzas se viola, equivale entonces a encontrar la firma de una o varias burbujas.
ii) La segunda categoría, la prueba en dos etapas de West (1987), se realiza en dos pasos y considera explícitamente en la hipótesis alternativa la posibilidad de la existencia de una burbuja. En la primera etapa se lleva a cabo una prueba de especificación del modelo, y una vez descartada una incorrecta especificación, en la segunda etapa se construye una prueba para detectar burbujas.
La idea del algoritmo plantea que es posible estimar una ecuación de Euler (base de la valoración de activos mediante la ley del precio único) en ausencia de burbujas, de la cual se obtiene una tasa de descuento factible. Entonces, si los dividendos pueden ser representados por un proceso autoregresivo (AR) y se tiene la identificación previa de la tasa de descuento, existe suficiente información para construir la relación entre los dividendos y los precios de mercado basados en los fundamentales. Por otra parte, la relación entre los precios de las acciones y los dividendos también puede ser directamente estimada mediante una regresión lineal. Bajo la hipótesis nula de la inexistencia de burbujas, la relación estimada directamente no debería diferir de la construida.
En otras palabras, la estimación de la Ecuación de Euler mediante el método de variables instrumentales provee estimativos del factor de descuento r. Esto, junto con el supuesto de que los dividendos siguen un proceso autoregresivo, provee una forma de recobrar el parámetro de autoregresión (φ), a través de una estimación lineal. West (1987) y Gurkaynak (2008) muestran que es posible representar el precio fundamental de mercado (de no arbitraje) mediante la siguiente relación:

donde  . Por su parte, el precio observado bien puede contener una burbuja. Bajo la hipótesis nula de que no la contiene, la estimación de β,
. Por su parte, el precio observado bien puede contener una burbuja. Bajo la hipótesis nula de que no la contiene, la estimación de β,  será insesgada:
será insesgada:

Por lo tanto, bajo una correcta hipótesis nula de no-burbujas, será igual  a
a  . Cualquier discrepancia podrá ser interpretada como un indicio de la presencia de burbujas en los datos.
. Cualquier discrepancia podrá ser interpretada como un indicio de la presencia de burbujas en los datos.
iii) El tercer grupo corresponde a las pruebas de integración y cointegración de las series de precios, desarrolladas principalmente por Diba y Grossman (1987; 1988). La idea central es imponer una estructura teórica a la forma de la burbuja. Los autores argumentan que si una burbuja existe, debe haberlo hecho desde el inicio de las transacciones, si los agentes son racionales y, por ende, se mantienen las condiciones de arbitraje. La ausencia de burbujas implicaría, entonces, grados específicos de estacionaridad en los dividendos y en los precios de las acciones y relaciones explícitas de cointegración entre ellos. La presencia de burbujas quebranta esta relación y, de esta forma, se genera información relevante para su detección empírica. Esto es:

ot denota los fundamentales no observables para el econometrista. Siempre que ot tenga un grado de integración menor que el de los dividendos y los precios, se cumple que la presencia de una burbuja en los datos rompe la relación de equilibrio (cointegración) entre estas dos variables.
Por tanto, una prueba de que Pt y dt tienen el mismo grado de integración y de que están cointegradas será suficiente para descartar la presencia de burbujas en los datos1.
Se podría considerar dentro de esta misma categoría el trabajo de Phillips, Shi y Yu (2012), quienes han desarrollado recientemente una prueba para identificar burbujas especulativas a través de regresiones recursivas, la cual involucra la construcción de estadísticos para poner a prueba una hipótesis de raíz unitaria versus alternativas explosivas, basándose en operadores supremos aplicados a pruebas tradicionales de raíz unitaria. Este procedimiento permite fechar las burbujas y sus colapsos periódicos y simultáneos en diferentes mercados. También cabe dentro de esta categoría el presente estudio, el cual está basado en una propuesta de uso de los test de signo, explorada en Uribe (2013), y que se discutirá en detalle en una sección posterior del documento.
iv) La categoría de burbujas intrínsecas explora un tipo diferente de burbujas, las cuales pueden o no estar correlacionadas con los fundamentales2.
Froot y Obstfeld (1991) muestran que si las burbujas dependen explícitamente de los fundamentales (los dividendos), por ejemplo mediante la

donde λes la raíz positiva de λ2σ2/2 + λμ - ln (1 + r) = 0 y c > 0. Si una burbuja de este tipo está presente en los datos, los precios de los activos serán más sensibles a las variaciones de los dividendos de lo que está justificado por la ecuación de valoración lineal tradicional, dada por:
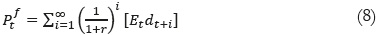
En consecuencia, se tendrá que la naturaleza de las burbujas intrínsecas impone algunas no linealidades en la razón precio/dividendo, que de otra forma no existirían (ésta sería constante). La presencia de tales no linealidades en los datos se interpreta como un indicio de la sobrerreacción de los precios ante las variaciones de los dividendos, debido a la presencia de burbujas.
Por último, Wu (1997) modela las burbujas como un vector de estado no observable en una representación estado-espacio, mediante un filtro de Kalman. Esta técnica le permite realizar una estimación óptima (de forma recursiva) del componente no observable (la burbuja) a través del tiempo, basándose en el modelo estructural especificado en la representación de estado-espacio y los datos disponibles para la estimación.
El componente de burbuja en este estudio es modelado como en:

donde ηt es ruido blanco y ψ es la razón promedio entre el precio y el precio más el dividendo, 0 < ψ < 1. La actualización de la burbuja se realiza de forma recursiva a medida que más datos entran en el sistema de estado-espacio, con ayuda del Filtro de Kalman.
Existen abundantes críticas a la literatura empírica para detectar burbujas. La mayoría de ellas se refieren a la dificultad que surge para decidirse en favor de la hipótesis de burbujas o de una incorrecta especificación de los modelos teórico y econométrico utilizados en la estimación. Por ejemplo, frecuentemente es difícil decidir si patrones no lineales en el comportamiento de las series se deben a la presencia de burbujas o a cambios estructurales en las series de los dividendos. Otra crítica muy relevante, en particular a las pruebas basadas en integración y cointegración, es la de Evans (1991). Este autor señala que los modelos basados en el algoritmo de Diba y Grossman (1987) tienen un pobre desempeño para detectar burbujas que colapsan periódicamente a un valor pequeño, pero ligeramente mayor que cero (con lo cual se seguiría cumpliendo la ley de arbitraje). Por ser de especial relevancia para la aplicación presentada en este documento, la crítica de Evans se describe a continuación.
B. El modelo de Evans
Como se mencionó antes, Evans (1991) ha subrayado una serie de críticas a las aproximaciones tradicionales para medir burbujas, tales como las propuestas por Diba y Grossman (1988) y Hamilton y Whiteman (1985). En líneas generales, el autor postula que estas pruebas tradicionales, basadas en el orden de integración y en la posible estimación de la cointegración de las series de precios y de sus fundamentales, pueden llevar a conclusiones erróneas. En particular pueden llevar a rechazar la hipótesis de burbujas cuando éstas están presentes en los datos. Evans muestra que las pruebas tradicionales de raíz unitaria versus alternativas explosivas a una cola tienen un desempeño muy pobre cuando se trata de detectar burbujas que colapsan periódicamente dentro de la muestra, con una probabilidad de colapso relativamente alta (mayor del 10%).
Evans simula un caso en el que las burbujas no son detectables por las pruebas tradicionales de raíz unitaria a una cola. Sea Ptf el componente fundamental de los precios y Bt uno de burbujas, de forma tal que:

donde k > 0 controla la magnitud relativa de los componentes fundamental y de burbuja.
Si supone que los dividendos siguen una caminata aleatoria del tipo:
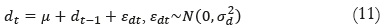
y por tanto, utilizando la Ecuación 8, en ausencia de burbujas se tiene que:

donde ρ-1 = 1 + r > 1 . También se supone que el componente de burbuja está descrito por el siguiente proceso aleatorio por tramos:

el cual tiene la propiedad de la submartingala, Et(Bt) = ρ-1Bt . εB,t+1 = exp(yt - τ2/2) con  son parámetros positivos con 0 < δ < ρ-1α, δ puede ser interpretado como el valor de reinicialización de la burbuja. θt+1 es un proceso Bernoulli (independiente de εB,t+1) que toma el valor de 1 con probabilidad π, y 0 con probabilidad 1 - π. Las ecuaciones 13 y 14 establecen que, mientras Bt < α, la burbuja crecerá a una tasa media de ρ-1. Cuando eventualmente Bt > α, la burbuja derivará en una fase en la cual su crecimiento será más rápido, igual a (πρ)-1. Esta aceleración en el crecimiento continuará hasta que la burbuja colapse, lo cual sucederá con una probabilidad de 1 - π.
son parámetros positivos con 0 < δ < ρ-1α, δ puede ser interpretado como el valor de reinicialización de la burbuja. θt+1 es un proceso Bernoulli (independiente de εB,t+1) que toma el valor de 1 con probabilidad π, y 0 con probabilidad 1 - π. Las ecuaciones 13 y 14 establecen que, mientras Bt < α, la burbuja crecerá a una tasa media de ρ-1. Cuando eventualmente Bt > α, la burbuja derivará en una fase en la cual su crecimiento será más rápido, igual a (πρ)-1. Esta aceleración en el crecimiento continuará hasta que la burbuja colapse, lo cual sucederá con una probabilidad de 1 - π.
En este caso se tendrá que la potencia de las pruebas tradicionales (su capacidad para rechazar las hipótesis nulas falsas de no burbujas) es muy pobre.
A la crítica de Evans es posible sumar un par de argumentos técnicos más, relacionados con el pobre desempeño de las pruebas tradicionales de raíz unitaria cuando son aplicadas a datos de frecuencia relativamente alta (diarios). En este tipo de datos la heteroscedasticidad condicional y la presencia de observaciones atípicas empobrecen el desempeño de las pruebas.
Con el fin de superar la crítica de Evans, una alternativa ha sido el desarrollo de algunos modelos con cambio de régimen (Hall, Psaradakis y Sola, 1999; Hall y Sola, 1993; Van Norden, 1996; Van Norden y Vigfusson, 1998), que buscan tener en cuenta la característica de colapso periódico de las burbujas y el comportamiento semi-estacionario que ésta induce sobre los datos. Estos modelos enfatizan en la dificultad empírica al tratar de diferenciar los comportamientos de burbuja de aquellos ocasionados por un cambio de régimen en los fundamentales de los precios.
Otra alternativa es realizar estimaciones reiteradas sobre muestras distintas para detectar la presencia de una raíz unitaria, versus alternativas explosivas. Phillips et al. (2012) exploran un procedimiento de mínimos cuadrados recursivos, en el cual, partiendo de una fracción de la muestra original r0,3 aplican una prueba de SupADF, definida en el texto de estos autores. La prueba se lleva a cabo sobre muestras que se incrementan de a una unidad (r1, r2, ..., rn donde ri = k+i/n).
Otra forma de proceder, la cual es preferida en este estudio por restarle inercia a la detección de las fechas de aparición de las burbujas con relación al procedimiento de Phillips et al. (2012), consiste en estimar las pruebas de raíz unitaria usando muestras seleccionadas con ventanas móviles de tamaño fijo, las cuales se mueven un periodo en cada paso de la estimación. En este procedimiento la selección del tamaño de la ventana es clave. En este estudio se sigue la recomendación de Uribe (2013) de trabajar con una ventana de 1000 datos, ventana que dentro de un conjunto discreto de alternativas ofrece mejor desempeño en términos de significancia empírica y potencia, al ser contrastada con el modelo de Evans, expuesto antes.4
III. Prueba de Signo para detectar burbujas
So y Shin (2001) proponen un test de signo para detectar caminatas aleatorias versus procesos alternativos generales y no estacionarios. El test es consistente ante una amplia gama de procesos no lineales, estacionarios o explosivos y tiene mejores propiedades en términos de poder asintótico local que alternativas tradicionales como las pruebas de Dickey-Fuller. También es invariante ante transformaciones monotónicas de los datos, heteroscedasticidad condicional de los errores y colas pesadas.
Si se tiene que:

donde {yt}, t = 0, ..., n, es un conjunto de observaciones, h(Pt) es una transformación monotónica desconocida de {Pt}ρ(Pt-1, ..., Pt-k), es un regresión desconocida de interés, k es un entero positivo, y {ut} es una secuencia de errores con mediana condicional igual a cero.
El interés se centra en probar la hipótesis nula H0:

es decir, en probar la hipótesis nula de caminata aleatoria versus la alternativa de un proceso explosivo lineal o no lineal bajo los supuestos 1 y 2.
Supuesto 1. {signo(ut)} es una secuencia de diferencias martingalas con respecto a una secuencia creciente de σ-anillos {Ft} tal que E[sing(ut)|Ft-1] = 0, t = 1,...,n.
Supuesto 2. P[ut| Ft-1] = 0
De esta forma, el estadístico de signo es definido por So y Shin (2001), es tal que si:

entonces se rechaza la hipótesis nula de caminata aleatoria expuesta en [16]. Aquí, signo(.) es el signo de ut, y está definido como signo(ut) = 1 si ut > 0, signo(0) = 0 y  es la mediana de {yt}nt=0; Bn(α) denota el α-ésimo cuantil de la distribución binomial con parámetros (n, 1/2); ρ = 1 y se trata de un proceso autoregresivo de orden 1. Las pruebas de este teorema y de algunas generalizaciones del mismo, así como las condiciones teóricas que deben ser satisfechas por las series bajo estudio para su correcta aplicación, son descritas de forma extensiva por So y Shin (2001).
es la mediana de {yt}nt=0; Bn(α) denota el α-ésimo cuantil de la distribución binomial con parámetros (n, 1/2); ρ = 1 y se trata de un proceso autoregresivo de orden 1. Las pruebas de este teorema y de algunas generalizaciones del mismo, así como las condiciones teóricas que deben ser satisfechas por las series bajo estudio para su correcta aplicación, son descritas de forma extensiva por So y Shin (2001).
En este estudio el test de signo con ajuste recursivo de mediana es aplicado a submuestras sucesivas, traslapadas, con el fin de evitar la crítica de Evans (1991) sobre los resultados. El tamaño de tales submuestras (l) es definido siguiendo las recomendaciones de Uribe (2013), quien realiza simulaciones para determinar la potencia y la significancia empíricas de la prueba ante diferentes longitudes de las ventanas. Los resultados de este autor se replican en el Apéndice 1 de este documento para el lector interesado.
A. Datos
En este estudio se utilizaron las series de índices de las bolsas de valores de seis mercados latinoamericanos: IPC de México, MERVAL de Argentina, BOVESPA de Brasil, IGPA de Chile, el Índice Morgan Stanley (MSCI) para Colombia5 y el IGBVL de Perú. Para el mercado estadounidense se utilizaron los índices NASDAQ y S&P500. El comportamiento de las tasas de interés de mercado en Estados Unidos se analizó siguiendo el comportamiento de la tasa de interés nominal de los títulos del Tesoro de Estados Unidos con vencimiento a 10 años y la tasa efectiva de los fondos de la Reserva Federal de los Estados Unidos (FED). Finalmente, dentro de las series de precios de los commodities se utilizaron el precio del oro y del petróleo West Texas Intermediate (WTI). Las series fueron consultadas en Datastream Internacional y en la página de Datos Económicos de la Reserva Federal (FRED por sus siglas en ingles), con la frecuencia con la que estaban disponibles. En un formato aaaa:mm:dd, todas las muestras llegan hasta 2013:03:29, con los periodos de inicio dados por: IPC(1988:01:04), MERVAL (1989:10:19), BOVESPA(1989:12:21), MSCI Colombia (1993:01:01), IGPA(1987:09:02), IGBVL(1991:02:01), NASDAQ(1971:02:05), SP500(1963:12:31), WTI(1986:01:02), ORO(1968:04:01), tasa de interés nominal 10 años (1962:01:02), y la tasa de los fondos federales (1954:07:01)
IV. Resultados
En el Gráfico 1 se presentan los índices analizados en niveles y se subrayan los periodos de burbujas detectados siguiendo la estimación del estadístico de signo y calculando el valor crítico con una significancia del 1% para la ventana de 1000 datos.
El Gráfico 1 permite dilucidar el crecimiento de las bolsas latinoamericanas en la época posterior a la crisis punto-com en Estados Unidos. Este crecimiento general marcó también una fuerte caída en los índices en la época posterior a las crisis subprime en el periodo 2007-2009. Colombia presenta una burbuja de mayor tamaño relativo a los demás países latinoamericanos desde el 2002, un año después de que se creara la Bolsa de Valores de Colombia (BVC) en julio de 2001. Brasil y Chile muestran rasgos prolongados de burbujas, para el primer mercado en el periodo 1993-1999, y para el segundo en el periodo entre 2004 y 2010.
Los commodities, el oro y el petróleo no muestran mayores signos de burbujas según las estimaciones. Existe un crecimiento de los precios cerca de 2001, año a partir del cual éstos mantuvieron un crecimiento continuo. Parte de la explicación de porqué no se detectan burbujas en la muestra podría estar relacionada con un fenómeno de flight-to-quality señalado por Caballero et al. (2008a). Cuando los inversionistas buscan activos menos riesgosos que los mercados accionarios para invertir, su paso por el mercado de commodities es relativamente corto. La estabilización del mercado podría producirse en un intervalo de tiempo menor al requerido para que el estadístico detecte la aparición de una burbuja; aun así, algunas burbujas de corta duración se detectan en los precios del petróleo y el oro, las cuales serán mencionadas más adelante.
En el Gráfico 2 se construye un índice de burbujas para cada serie, en el cual se pueden apreciar las magnitudes relativas de las mismas en el tiempo. El índice de burbujas se definió así:

donde BIt es el índice de burbujas en el periodo t, N es el tamaño de la ventana y l es el tamaño de la ventana móvil, en este caso 1000. El número cv:= [n - 2Bn(α)] es el α-iésimo percentil de la distribución binomial con parámetros (l, 1/2)Snt. es el estadístico definido en la Ecuación 18 en el periodo t, con ρ = 1. Entonces, la fecha de comienzo de la burbuja está dada por:

Análogamente la fecha de colapso está dada por

donde tiB es el periodo tj que marca el comienzo de la burbuja, tiE es el periodo tk que marca el final de la burbuja, tk y tj son números naturales tales que tj, tk ∈ t; e i es un número natural que se usa para identificar la burbuja. Este procedimiento sirve para fechar múltiples burbujas en la serie, si existe evidencia de alguna.
Del análisis de los Gráficos 1-7, así como de la Tabla 1, se tiene que el modelo de Caballero et al. (2008a) parece proveer una historia coherente para explicar la dinámica de los índices de precios de los mercados latinoamericanos más grandes, en periodos recientes. Se presenta un claro colapso de las burbujas en los mercados latinoamericanos a mediados y fi nales de la década de los noventa. Estos periodos de colapso corresponden con las épocas de inicio de las burbujas en varios mercados estadounidenses, medidos por el SP500 y el NASDAQ. La época de aparición de las burbujas corresponde de forma cercana, a su vez, con un periodo de tasas de interés de mercado bajas, y el descenso de estas tasas corresponde, a su vez, con la aparición de burbujas de corta duración en algunos mercados de commodities, principalmente el oro.
Por otra parte, algunos hechos parecen salirse de la historia predicha. Por ejemplo, el periodo de inflación de las burbujas cerca del año 2004 en el mercado estadounidense, después del colapso de las burbujas punto-com en el mercado de empresas de información y tecnologías (medidas por el NASDAQ), también se empareja con un periodo de nuevas burbujas en los mercados accionarios de Latinoamérica, rompiéndose la sincronía entre las fechas de colapso y origen que caracterizó la década de los noventa. No obstante, hay que llamar la atención sobre el hecho de que este patrón también es consistente con una oferta relativamente escasa de instrumentos financieros sólidos y líquidos alrededor del mundo. Podría haber ocurrido que parte de los capitales se hayan invertido en EEUU y otra parte en los mercados emergentes más grandes de la región.
También es notable el hecho de que para los años 2010-2011 las burbujas en los mercados estadounidenses parecían llegar a su fin, en tanto que las de Latinoamérica comenzaban a cobrar nueva tracción. A fines de la muestra no es posible descartar la presencia de burbujas en los mercados del continente americano. Lo anterior podría ser consecuencia del desplazamiento de capitales desde la inversión en commodities, en bonos de empresas y deudas soberanas en países de Europa Mediterránea hacia estos mercados.
Conclusiones, recomendaciones y limitaciones del análisis
El principal aporte de este estudio a la literatura consiste en identificar periodos de burbujas en los mercados de acciones más grandes de Latinoamérica con una técnica de reciente desarrollo. Estos periodos coinciden con una historia de flujos de capitales de portafolio, que escapan sistemáticamente de crisis y depresiones bursátiles alrededor del mundo, los cuales conllevan en su dinámica la creación y desaparición de burbujas en la región de forma más o menos sincronizada.
El patrón identificado da respaldo a la tesis de Caballero et al. (2008a) sobre la generación de burbujas en Estados Unidos, a causa de una oferta mundial inelástica y bastante escasa de instrumentos financieros líquidos y sólidos, que se ve fácilmente superada por una demanda creciente de instrumentos sofisticados de ahorro. La historia puede ser complementada con una hipótesis sobre un posible spillover de este fenómeno en épocas recientes, desde el mercado norteamericano hacia los mercados de acciones latinoamericanos. Lo anterior podría explicar la conformación de burbujas simultáneas en la década más reciente del estudio (a partir de 2004), tanto en el hemisferio norte como en el sur del continente.
Para Caballero et al. (2008a) el fenómeno es consecuencia de varios factores conjugados: como se dijo antes, una oferta limitada y asimétrica de activos financieros líquidos y sólidos alrededor del mundo. En segundo lugar, una política de tasas de interés bajas durante un periodo de tiempo prolongado (factor que también ha sido señalado por otras fuentes como Schwartz, 2009), la cual, sumada con el ingreso creciente de capitales externos a la economía americana, influyó fuertemente en la mantención de tasas de interés de mercado excesivamente bajas, que potenciaron la formación de burbujas en ese mercado. Estas burbujas serían las mismas que posteriormente migrarían a los demás mercados (commodities, y según una interpretación propia, también los mercados accionarios de países emergentes de América Latina). Finalmente, Caballero et al. (2008b) identifican un desbalance global comercial (que es el espejo del desbalance en la cuenta de capitales) de la economía norteamericana con respecto al resto del mundo, en particular con Asia y los países productores de petróleo, el cual también contribuye a la generación de estas burbujas.
Vistos así, la aparición y el colapso de las burbujas en Latinoamérica lucen más como fenómenos determinados desde afuera, que no están a merced de alguna variable de control de la política interna de los países de la región. No obstante, el solo hecho de pensar en la posibilidad de identificar una burbuja y en la construcción de técnicas de pronóstico con base en los indicadores presentados u otros disponibles en la literatura, como las razones de varianza dinámicas (exploradas en Uribe y Ulloa, 2011) y las técnicas de mínimos cuadrados recursivos para la detección de raíces unitarias a través de pruebas SupADF al estilo planteado por Phillips et al. (2012), permite levantar algunos cuestionamientos sobre la optimalidad de los esquemas de inflación objetivo tradicionales, que operan en gran parte de la región. Estos esquemas dejan los precios de los activos financieros (con una excepción parcial de los precios de las viviendas) por fuera del alcance de la política monetaria.
También es posible señalar la necesidad de coordinar las políticas macroeconómicas de la región con el fin de tratar de disminuir los impactos negativos de la entrada de capitales a los países del bloque, y sobre todo los efectos negativos de las salidas abruptas de los mismos.
NOTAS
1 El componente de burbujas es no invertible y no estacionario, sin importar el número de diferencias que se tomen a los datos tal y como es anotado por Diba y Grossman (1987).
2 De la Ecuación 4, nótese que el tipo de burbujas que puede ser detectado usando las pruebas en dos etapas de West es solo el de aquellas que están correlacionadas con los fundamentales.
3 es el tamaño de la muestra
es el tamaño de la muestra
4 En el Apéndice del documento se replican los resultados de Uribe (2013) al respecto.
5 No se utilizó ninguno de los índices de este mercado, IGBC, Colcap y Col20, puesto que están disponibles solo desde 2001 y 2008 respectivamente, lo cual dificultó las comparaciones con los demás mercados.
REFERENCIAS
Abreu, Dilip y Brunnermeier, Marcus (2003). ''Bubbles and Crashes'', Econometrica, Vol. 71, Issue 1, pp. 173-204. [ Links ]
Allen, Franklin y Gale, Douglas (2000). ''Bubbles and crises'', The Economic Journal, Vol. 110, Issue 460, pp. 236–255. [ Links ]
Branchs, William y Evans, George (2011). ''Learning about Risk and Return: A Simple Model of Bubbles and Crashes'', American Economic Journal: Macroeconomics, Vol. 3, Issue 3, pp. 159-191. [ Links ]
Caballero, Ricardo; Farhi, Emmanuel y Gourinchas, Pierre-Olivier (2008a). ''Financial Crash, Commodity Prices and Global Imbalances'', Brookings Papers on Economic Activity, Fall, pp. 1-55. [ Links ]
Caballero, Ricardo; Farhi, Emmanuel y Gourinchas, Pierre-Olivier (2008b). ''An Equilibrium Model Of Global Imbalances and Low Interest Rate'', American Economic Review, Vol. 98, Issue 1, pp. 358-393. [ Links ]
Diba, Behzad y Grossman, Herschel (1987). ''On the inception of rational bubble'', Quarterly Journal of Economics, Vol. 87, Issue 3, pp. 697–700. [ Links ]
Diba, Behzad y Grossman, Herschel (1988). ''The theory of rational bubbles in stock prices'', The Economic Journal, 98, Issue 392, pp. 746–754. [ Links ]
Evans, George (1991). ''Pitfalls in testing for explosive bubbles in asset prices'', American Economic Review, Vol. 81, Issue 4, pp. 922–930. [ Links ]
Farmer, Roger E. A. (2012). ''Confidence, crashes and animal spirits'', Economic Journal, Vol. 122, Issue 559, pp. 155–172. [ Links ]
Froot, Kenneth y Obstfeld, Maurice (1991). ''Intrinsic bubbles: the case of stock prices'', American Economic Review, Vol. 81, Issue 5, pp. 1189–1214. [ Links ]
Gurkaynak, Refet (2008). ''Econometrics Test of Asset Price Bubbles: Taking Stock'', Journal of Economic Surveys, Vol. 22, Issue 1, pp. 166-186. [ Links ]
Hall, Stephen y Sola, Martin(1993). ''Testing for Collapsing Bubbles: an Endogenous Switching ADF test'', Discussion Paper, pp. 15-93. London Business School. [ Links ]
Hall, Stephen; Psaradakis, Zacharias y Sola, Martin (1999). ''Detecting Periodically Collapsing Bubbles: a Markov-Switching Unit Root Test'', Journal of Applied Econometrics, Vol.14, Issue 2, pp. 143–154. [ Links ]
Hamilton, James y Whiteman, Charles(1985). ''The observable implications of self-fulfilling expectations'', Journal of Monetary Economics, Vol.16, Issue 3, pp. 353–373. [ Links ]
Hoover, Kevin; Johansen, Søren y Juselius, Katarina (2008). ''Allowing the Data to Speak Freely: The Macroeconometrics of the Cointegrated Vector Autoregression'', American Economic Review, Vol. 98, Issue 2, pp. 251-255. [ Links ]
LeRoy, Stephen y Porter, Richard (1981). ''The present-value relation: tests based on implied variance Bounds'', Econometrica, Vol. 49, pp. 555–574. [ Links ]
Phillips, Peter C.B.; Shi, Shu-Ping y Yu, Jun (2012). ''Testing for multiple bubbles''. Cowles Foundation Discussion Paper, 1843. Yale University. Recuperado de: http://cowles.econ.yale.edu/P/cd/d18a/d1843.pdf (15 de Enero de 2014). [ Links ]
Samuelson, Paul (1958). ''An exact consumption-loan model of interest with or without the social contrivance of money'', Journal of Political Economy, Vol. 66, Issue 6, pp. 467–482. [ Links ]
Schwartz, Anna (2009). ''Origins of Financial Markets Crisis of 2008''. En: Booth, Philip (Ed.), Verdict on the Crash: Causes and Policy Implications (45-50). London: The Institute of Economic Affairs. [ Links ]
Shell, Karl (1971). ''Notes on the Economics of Infinity'', Journal of Political Economy, Vol. 79, Issue 5, pp. 1002-1011. [ Links ]
Shiller, Robert (1981). ''Do stock prices move too much to be justified by subsequent changes in dividends?'', American Economic Review, Vol.71, pp. 421–436. [ Links ]
Shiller, Robert (2000). Irrational Exuberance. Princeton: Princeton University Press. [ Links ]
So, Beong Soo y Shin, Dong Wan (2001). ''An Invariant Sign Test for Radom Walks Base On Recursive Median Adjustment'', Journal of Econometrics, Vol. 102, Issue 2, pp. 197-229. [ Links ]
Tirole, Jean (1982). ''On the Impossibility of Speculation Under Rational Expectations'', Econometrica, Vol. 50, Issue 5, pp. 1163–1181. [ Links ]
Tirole, Jean (1985). ''Asset bubbles and overlapping generations'', Econometrica, Vol. 53, Issue 6, pp. 1499–1528. [ Links ]
Uribe, Jorge Mario(2013). ''Testing for Multiple Bubbles with Daily Data''. Documento de trabajo. Banco de la República de Colombia. Recuperado de: http://banrep.gov.co/en/node/32390 (15 de Enero de 2014). [ Links ]
Uribe, Jorge Mario y Ulloa, Inés María (2011). ''Revisando la hipótesis de los mercados eficientes: nuevos datos, nuevas crisis y nuevas estimaciones'', Revista Cuadernos de Economía, Vol. 30, No. 55, pp. 127-154. [ Links ]
van Norden, Simon (1996). ''Regime Switching as a Test for Exchange Rate Bubbles'', Journal of Applied Econometrics, Vol. 11, Issue 3, pp. 219-51. [ Links ]
van Norden, Simon y Vigfusson, Robert (1998). ''Avoiding the pitfalls: can regime-switching tests reliably detect bubbles?'', Studies in Nonlinear Dynamics and Econometrics, Vol. 3, pp. 1–22. [ Links ]
West, Kenneth (1987). ''A specification test for speculative bubbles'', Quarterly Journal of Economics, Vol. 102, Issue 3, pp. 553–580. [ Links ]
Wu, Yangru (1997). ''Rational bubbles in the stock market: accounting for the U.S. stock-price volatility'', Economic Inquiry, Vol. 35, Issue 2, pp. 309–319. [ Links ]
La longitud de la ventana móvil es un aspecto fundamental en la estimación dinámica de las burbujas. En este apéndice se replican los resultados encontrados por Uribe (2013) al respecto, para el lector interesado.
En la Tabla 2 se presentan las significancias empíricas en diferentes percentiles α-ésimos de la distribución binomial.
Con el fin de determinar la longitud óptima de las ventanas móviles, se exploran las Tablas 2 y 3. En términos de potencia (Tabla 3) luce óptimo trabajar con ventanas de mayor longitud, sin embargo, existe un trade-off de ese criterio, tanto con las pérdidas en términos de ajuste de la significancia empírica (Tabla 2) como con la necesidad teórica de identificar periodos de origen y de colapso de las burbujas dinámicamente. Por lo anterior se prefiere utilizar un criterio alternativo: trabajar con las ventanas de menor longitud posible, pero aprovechando de la mejor forma los incrementos marginales en la longitud de las ventanas, en términos de potencia. En la Tabla 4 se reportan estas ''ganancias'' en términos de potencia, cada vez que la ventana se incrementa en 500 datos.
Después de realizar un análisis conjunto de los resultados en las Tablas de la 2 a la 4, Uribe (2013) sugiere trabajar con ventanas entre 500 y 1500 datos. Con una estimación puntual de 1000 datos, que fue la seguida aquí.























