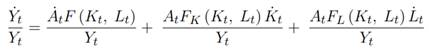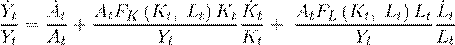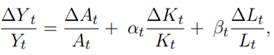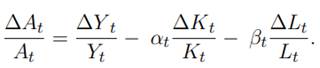Introducción
El problema principal que se enfrenta al intentar comprender el crecimiento y desarrollo económico no es entender el proceso por el cual una economía incrementa su tasa de ahorro y la acumulación de capital físico. Lo cierto es que, aunque la acumulación de factores productivos se considera la principal fuente de empuje para el crecimiento económico, existe “algo más” que nos ayuda determinar las diferencias de crecimiento del PIB e ingresos per cápita entre países, incluso cuando se toma en cuenta el capital físico y humano. A ese factor se le conoce como productividad total de los factores (PTF) (Easterly y Levine, 2001; Koutun y Karabona, 2013).
La PTF es la fracción de la producción agregada que no se explica por los cambios en los factores productivos dentro de la función de producción (Comin, 2006; Van Ark, 2014; Bejarano et al., 2018; Huggett, 2018). Desde su incorporación a la literatura del crecimiento por parte de Robert Solow (1957), el cálculo en forma de residual de la PTF y la medición de esta se han mantenido vigentes como objeto de estudio e investigación cuya finalidad es determinar el desempeño económico de las naciones. Es por ello que la PTF se ha convertido sin duda en el residuo más famoso y celebrado en la ciencia económica, así como lo demuestran los innumerables artículos académicos, reseñas y libros dedicados al tema, sin mencionar los millones de horas invertidas en la conceptualización, medición e interpretación de la PTF por parte de la comunidad científico-académica mundial (Canarella y Pollard, 2003; Van Ark, 2014).
A partir de lo anterior, puede que surja la pregunta ¿por qué está la ciencia económica tan interesada en la productividad?, la respuesta yace en que la productividad es una de las razones fundamentales por la cual existen grandes diferencias en los niveles de vida a nivel mundial, ya que sin productividad las economías desacelerarían lentamente hasta estancarse y, además, es la única fuente de crecimiento a largo plazo que no sufre de retornos decrecientes como lo hacen los factores productivos homogéneos (Van Ark, 2014). Por ello, la finalidad del presente artículo fue analizar la productividad total de los factores en la región de América del Sur, subregión de mucha importancia en el crecimiento del continente americano en su totalidad, en el período 1950-2014 aplicando el modelo Solow-Swan ampliado, según la propuesta de Mankiw et al. (1992), aportando conocimientos para Suramérica que pueden ser comparados con otras investigaciones en el área neurálgica del crecimiento económico. El artículo se divide en cuatro partes comenzando por la revisión de la literatura, continuando con el modelo econométrico a ser utilizado para especificar, posteriormente, la estimación de las elasticidades del producto respecto a los factores productivos capital y trabajo en la región, lo cual es un insumo para el propósito de analizar la productividad total de los factores de esta bajo el enfoque del modelo de Solow-Swan ampliado, finalizando con las conclusiones propuestas.
No obstante, debemos destacar que este estudio no intenta argumentar que la acumulación de factores no es importante en términos generales o negar que sea posiblemente importante para diversos países en distintas coyunturas. La PTF no tiene la capacidad de explicarlo todo, en todas partes o en todo momento. En su lugar, esta investigación argumenta que existen factores fuera de la acumulación que juegan un rol importante a la hora de explicar las diferencias de desempeño económico entre países (Easterly y Levine 2001; Canarella y Pollard, 2003; Koutun y Karabona 2013).
I. Revisión de la literatura
A. Función de producción Cobb-Douglas
Desarrollada por el matemático Charles Cobb y el economista Paul Douglas (Briones et al., 2018), es la función de producción más utilizada en economía para describir la cantidad de producto que genera la utilización de los factores capital (K) y trabajo (L) en el proceso de producción. Es por ello por lo que esta función es muy útil, debido a que arroja una descripción muy precisa de la economía y es fácil trabajarla algebraicamente (Acemoglu, 2009). La función entonces tiene la siguiente forma:
donde:
Y t = Producción agregada
A t = Progreso tecnológico o Productividad Total de los Factores (PTF)
K t = Stock de capital
L t = Número de trabajadores ocupados
α = Elasticidad de la producción agregada con respecto al factor capital β = Elasticidad de la producción agregada con respecto al factor trabajo
Adicionalmente, esta función posee tres características que facilitan la explicación de fenómenos y teorías macroeconómicas:
Exhibe rendimientos constantes a escala: los rendimientos a escala miden la variación de la producción ante un cambio proporcional en todos los factores, es decir, si α+β = 1, se obtienen retornos constantes a escala. Si α + β > 1, se obtienen retornos crecientes a escala y, por último, si α + β < 1, se obtienen retornos decrecientes a escala.
Exhibe productividad marginal positiva y decreciente. Esta propiedad refleja la ley de rendimientos decrecientes de los factores, la cual indica que a medida que uno de los factores de producción aumenta, mientras que el resto se mantiene constante, entonces su productividad marginal va decayendo.
Exhibe elasticidad de producción constante. La elasticidad de producción mide la variación porcentual de la producción ante un cambio en los insumos utilizados. En este caso es constante e igual a α para el capital y β para el trabajo. Dentro de este contexto, la función de producción Cobb-Douglas a su vez mantiene las mismas características que la función de producción neoclásica básica. Es decir que presenta rendimientos a escala constantes, los productos marginales del capital y del trabajo son positivos, los productos marginales son decrecientes y se satisfacen las condiciones de Inada (Sala-i-Martin, 2000).
B. Modelo Solow-Swan ampliado
El modelo Solow-Swan clásico propone que se estudie el crecimiento económico asumiendo una función de producción estándar con rendimientos decrecientes en el factor capital (K), tomando las tasas de ahorro y de crecimiento de la población como exógenas. Solow demostró que estas dos variables determinarían el ingreso per cápita durante el estado estacionario, debido a que las tasas de crecimiento del ahorro y la población varían entre países, y por ello llegan a diferentes estados estacionarios. La conclusión básica sería entonces que mientras más altas sean las tasas de ahorro más ricos serán los países (mayor nivel de ingreso per cápita), y mientras más altas sean las tasas de crecimiento de la población más pobres serán los países (menor nivel de ingreso per cápita) (Solow, 1956; Mankiw et al., 1992).
Basándose en ello, los autores Mankiw, Romer y Weil (Mankiw et al., 1992), describen que las predicciones del modelo de Solow-Swan (1956) no son más que una primera aproximación consistente con la evidencia empírica. Al examinar datos para 1992 sobre un gran número de países, Mankiw et al. (1992) encontraron que el crecimiento del ahorro y de la población, afecta directamente el ingreso per cápita en la dirección que Solow predijo. Inclusive, más de la mitad de las diferencias del ingreso per cápita entre países puede ser explicada por esas variables solamente.
Sin embargo, no todo va bien en el Modelo Solow-Swan porque, aunque predice correctamente la dirección de los efectos del crecimiento del ahorro y de la población, no predice correctamente las magnitudes en las que lo hace, ya que en la data usada los efectos de ambas variables sobre el ingreso son demasiado grandes. Es por ello que, para entender la relación entre ahorro, población y crecimiento, se debe ir más allá del modelo Solow-Swan clásico, lo cual proveería una excelente herramienta para la descripción y el análisis de la data concerniente a las diferencias de ingreso per cápita entre países (Mankiw et al., 1992).
A partir de ello, Mankiw et al. (1992), basándose en el modelo de 1956, desarrollaron lo que se denominaría modelo Solow-Swan ampliado o MRW (en referencia a los nombres de los autores), por medio de la inclusión de la acumulación de capital humano (H) y de capital físico (K). En este contexto, por capital humano se entiende el conjunto de conocimientos, habilidades, cualidades y destrezas que poseen y utilizan los trabajadores (L) de la economía en sus actividades profesionales, dando a espacio a que aumenten su productividad y sus remuneraciones por encima del promedio poblacional (Blanchard et al., 2012). Argumentando la exclusión del capital humano (H) en el modelo Solow-Swan clásico, potencialmente, explica las razones por las cuales la influencia estimada de las tasas de crecimiento del ahorro y la población resulta demasiado grande:
Primero, a cualquier tasa dada de acumulación de capital humano (H), mayor tasa de ahorro o menor tasa de crecimiento de la población conlleva a niveles más altos de ingreso y por ello a niveles más altos de capital humano (H). Entonces, la acumulación de capital físico (K) y crecimiento de la población tienen un mayor impacto sobre el ingreso, cuando la acumulación de capital humano (H) se toma en cuenta (Mankiw et al., 1992).
Segundo, la acumulación de capital humano (H), puede estar correlacionada con las tasas de ahorro y las tasas de crecimiento de la población, lo que implicaría que omitir la acumulación de capital humano (H) influye sobre los coeficientes estimados sobre el ahorro y el crecimiento de la población (Mankiw et al., 1992).
En el mismo orden de ideas, una vez se incluye el capital humano en la ecuación, partiendo de una función de producción Cobb-Douglas, el modelo toma la forma de:
donde:
Y t = Producción agregada
K t = Stock de capital
H t = Stock de capital humano
A t = Cambio tecnológico, o Productividad total de los factores (PTF) L t = Número de trabajadores α = Elasticidad de la producción agregada con respecto al factor capital β = Elasticidad de la producción agregada con respecto al factor trabajo
Este modelo asume que, por medio de la función de producción, cualquier unidad de consumo puede ser transformada sin esfuerzo a una de capital físico (K) o capital humano (H), mientras que ambos factores de capital (K y H) se depreciaren a tasas iguales. Adicionalmente, se asume que α + β < 1, lo cual implicaría que existen rendimientos decrecientes en ambos factores de capital. Si α+β = 1, entonces existirán rendimientos constantes a escala en los factores reproducibles, lo cual significa que no existe un estado estacionario para el modelo (Mankiw et al., 1992). Así, este modelo de crecimiento tiene diversas implicaciones:
En primer lugar, la elasticidad del ingreso con respecto al stock de capital físico (K) no es sustancialmente diferente de la participación de los capitales en el ingreso. En otras palabras, no existen externalidades sustanciales para la acumulación de capital físico (K) (Mankiw et al., 1992).
En segundo lugar, a pesar de la ausencia de externalidades, la acumulación de capital físico (K) tiene un mayor impacto sobre el ingreso per cápita de lo que implica el modelo estándar de Solow-Swan. Mayores tasas de ahorro llevan a un mayor nivel de ingresos en el estado estacionario, lo que a su vez resulta en un nivel más alto de capital humano (H), incluso si el nivel de acumulación de capital humano (H) permanece constante. Mayores niveles de ahorro, entonces, aumentarán la PTF como suele medirse (Solow, 1956; Mankiw et al., 1992).
En tercer lugar, el crecimiento de la población también presenta un mayor impacto sobre el ingreso per cápita de lo que indica el modelo estándar, debido a que en estos altos niveles de crecimiento de la población, tiene como resultado que se reduzca el ingreso per cápita, ya que las cantidades del capital físico (K) y humano (H) disponibles deberán repartirse de forma cada vez menor sobre el total de la población (Mankiw et al., 1992).
En el modelo ampliado el capital humano (H) también debe distribuirse de manera más escasa, lo que implica que mayores tasas de crecimiento de la población reducirá la PTF medida (Mankiw et al., 1992; Solow, 1956).
Por último, el modelo tiene implicaciones para la dinámica de la economía cuando esta no se encuentra en el estado estacionario, prediciendo que los países con niveles de tecnología (A), tasas de acumulación y de crecimiento de la población similares deberían converger en sus ingresos per cápita, sin embargo, esta convergencia ocurre más lentamente de lo que el modelo Solow-Swan de 1956 sugiere, ya que este implica que una economía alcanzara la mitad de su estado estacionario dentro del modelo en alrededor de 17 años. Mientras que el modelo ampliado implica ese punto se alcanzara en alrededor de 35 años (Solow, 1956; Mankiw et al., 1992).
C. Contabilidad del crecimiento en el marco del modelo de Solow-Swan ampliado
A través de otro de sus trabajos pioneros Solow (1957) proporcionó una metodología con la cual es posible medir la contribución de los distintos factores de producción y del crecimiento del avance tecnológico o PTF sobre la tasa de crecimiento de la producción agregada de la economía, la cual se le denomina contabilidad del crecimiento (Sala-i-Martin, 2000; Barro y Sala-iMartin, 2009; Romer, 2012).
La contabilidad del crecimiento divide el crecimiento de la producción de una firma o un país en dos partes. La primera corresponde al de la producción, que puede atribuirse al crecimiento de los distintos factores productivos, manteniendo a la tecnología como constante, mientras que la segunda parte es el crecimiento que puede atribuirse solo al incremento o disminución en la tecnología (Huggett, 2018). En este contexto, el análisis de la contabilidad del crecimiento inicia a partir de la función de producción neoclásica (3) que se reproduce aquí (Huggett, 2018):
Aplicando diferenciación total y parcial con respecto al tiempo en la ecuación (3) se tiene:
Ahora, derivando Y con respecto a las variables A, K y L se obtiene:
Denotando la expresión
 con el símbolo α
t
, y la expresión
con el símbolo α
t
, y la expresión
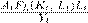 con el símbolo β
t
, se obtiene:
con el símbolo β
t
, se obtiene:
Donde, α t representa la participación del factor capital dentro de la producción total y β t representa la participación del factor trabajo dentro de la producción total. Posteriormente se hace la aproximación de las tasas de crecimiento graduales sujetas a estudio, con respecto a otras tasas de crecimiento de períodos de tiempo inmediatos a estas aplicando primeras diferencias. Es decir:
Obteniendo así la ecuación fundamental de la contabilidad del crecimiento de Solow:
donde:
 = Tasa de crecimiento de la producción agregada
= Tasa de crecimiento de la producción agregada
 = Cambio tecnológico, o productividad total de los factores (PTF)
= Cambio tecnológico, o productividad total de los factores (PTF)
 = Tasa de crecimiento del stock de capital físico
= Tasa de crecimiento del stock de capital físico
 = Tasa de crecimiento del factor trabajo
= Tasa de crecimiento del factor trabajo
En este sentido, la ecuación 12 indica que el crecimiento de la producción agregada de la economía es igual a la suma de la tasa de crecimiento tecnológico
 (o PTF), la tasa de crecimiento del capital multiplicado por α
t
, y la tasa de crecimiento del factor trabajo multiplicado por β
t
(Huggett, 2018).
(o PTF), la tasa de crecimiento del capital multiplicado por α
t
, y la tasa de crecimiento del factor trabajo multiplicado por β
t
(Huggett, 2018).
Conforme a ello, la contabilidad del crecimiento considera que la tecnología se puede representar con una función de producción agregada. Sin embargo, algunos autores alegan que la misma no tiene la capacidad de explicar cómo o por qué crece el nivel de tecnología en las economías (Huggett, 2018; Jiménez, 2011; Acemoglu, 2009). No obstante, Solow (1957) sostuvo que existe la necesidad de medir la tasa de crecimiento de la tecnología
 , entre períodos de forma residual, resultado de la diferencia entre la producción agregada y el crecimiento de los factores productivos observados. Es decir:
, entre períodos de forma residual, resultado de la diferencia entre la producción agregada y el crecimiento de los factores productivos observados. Es decir:
Esta ecuación, que posteriormente se denominaría como “Residuo de Solow”, implica que el crecimiento observado de
 , es una medida efectiva del avance tecnológico debido a que por medio de esta se recopila cualquier error ocurrido en las estimaciones de todas las demás variables que entran en la ecuación de la contabilidad del crecimiento (Solow, 1957), es decir que la PTF es la fracción de la producción agregada que no está explicada por los cambios en los factores productivos dentro de la función de producción (Comin, 2006; Huggett, 2018).
, es una medida efectiva del avance tecnológico debido a que por medio de esta se recopila cualquier error ocurrido en las estimaciones de todas las demás variables que entran en la ecuación de la contabilidad del crecimiento (Solow, 1957), es decir que la PTF es la fracción de la producción agregada que no está explicada por los cambios en los factores productivos dentro de la función de producción (Comin, 2006; Huggett, 2018).
Ahora bien, en el marco del modelo Solow-Swan ampliado, una manera alternativa de estimar la contabilidad del crecimiento se puede lograr a través de una función de producción en forma intensiva, es decir en términos por trabajador. Sea la función Cobb-Douglas:
donde:
Y t = Producción agregada
K t = Stock de capital
HL t = Factor trabajo (ajustado por una medida de capital humano) A t = Cambio tecnológico, o PTF α = Elasticidad de la producción agregada con respecto al factor capital β = Elasticidad de la producción agregada con respecto al factor trabajo
De igual manera, existe otro modo de realizar el ejercicio de la contabilidad del crecimiento, el cual consiste en llevar la función de producción Cobb-Douglas a términos por trabajador, es decir dividiendo la función entre el factor trabajo (HL):
obteniendo así la función de producción Cobb-Douglas en su forma intensiva, conforme a lo establecido por Mora (2006):
donde:
y t = Producto por trabajador (medido con un ajuste por capital humano) A t = Cambio tecnológico o PTF k t = Stock de capital físico por trabajador (medido con un ajuste por capital humano).
Tomando logaritmos de ambos lados de la ecuación 16, y diferenciando con respecto al tiempo, se obtiene la ecuación fundamental de la contabilidad del crecimiento, pero en términos intensivos bajo el enfoque del modelo Solow-Swan ampliado, debido a la inclusión del capital humano como medida de ajuste al factor trabajo:
donde:
 = Tasa de crecimiento del producto por trabajador (medido con un ajuste por capital humano)
= Tasa de crecimiento del producto por trabajador (medido con un ajuste por capital humano)
 = Tasa de crecimiento del stock de capital físico por trabajador
= Tasa de crecimiento del stock de capital físico por trabajador
(medido con un ajuste por capital humano) α = Elasticidad de la producción agregada con respecto al factor capital Por último, a la hora de estimar el residuo de Solow, o el crecimiento de
 , la ecuación resultante es:
, la ecuación resultante es:
II. Modelo econométrico
Los datos empleados se tomaron de la Penn World Table (PWT, por sus siglas en inglés) versión 9.0 la cual es una base de datos con información sobre niveles relativos de ingresos, producción, insumos y productividad, que cubre 182 países entre 1950 y 2014 (Feenstra, Inklaar y Timmer, 2015), empleando para su análisis el paquete econométrico Eviews.
El modelo para aplicar la contabilidad del crecimiento será de regresión lineal bajo el método de mínimos cuadrados ordinarios (MCO), con datos en series de tiempo a partir de la función de producción Cobb-Douglas en términos intensivos con la adición del capital humano según la propuesta de Mankiw et al. (1992).
Sin embargo, existe una restricción impuesta por el primer supuesto para la estimación de modelos de regresión lineal, el cual establece que se requiere partir de una función lineal en los parámetros (Gujarati y Porter 2010). Dado que la ecuación base de esta investigación es la función Cobb-Douglas, esta condición no se cumple por lo que es necesaria linealizarla. Dado esto, sea la función (19):
donde:
y t = Producto por trabajador (medido con un ajuste por capital humano sobre la base de años de escolaridad) A t = Cambio tecnológico o PTF.
k t = Stock de capital físico por trabajador (medido con un ajuste por capital humano sobre la base de años de escolaridad) α = Elasticidad del producto con respecto al capital físico.
En orden de obtener una función lineal, se recurrirá a transformarla en una función Cobb-Douglas log-linealizada, a través de la implementación de logaritmos naturales, aprovechando las propiedades de suavización y las propiedades que presenta este método matemático como, lo establecen Chiang y Wainwright (2007):
donde:
Ln y t = Logaritmo natural del producto por trabajador (medido con un ajuste por capital humano sobre la base de años de escolaridad).
Ln k t = Logaritmo natural del stock de capital por trabajador (medido con un ajuste por capital humano sobre la base de años de escolaridad). Ln A t = Productividad total de los factores.
Por otra parte, se procede a aplicar primeras diferencias a la serie de datos en el período abarcado por el estudio (1950-2014), para calcular las tasas de crecimiento de las variables en dicho período para cada país, obteniendo:
Ahora especificamos el modelo econométrico como:
Sin embargo, persiste el problema de poder observar directamente el crecimiento de la tecnología o PTF. Es por ello que se recurre a medirla a través de la metodología suministrada por Solow (1957) discutida en secciones anteriores, teniendo como resultado la ecuación se transforme en:
donde:
∆Ln A t = Productividad total de los factores.
∆Ln y t = Tasa de crecimiento del producto por trabajador (medido con un ajuste por capital humano sobre la base de años de escolaridad).
∆Ln k t = Tasa de crecimiento del capital por trabajador (medido con un ajuste por capital humano sobre la base de años de escolaridad) β 0 = Elasticidad del producto con respecto al capital físico µ t = Término de error o perturbación.
III. Estimación de las elasticidades del producto respecto a los factores productivos capital y trabajo
Se especificó un modelo sobre la base de la función de producción CobbDouglas en términos intensivos con la adición del capital humano (Mankiw et al., 1992):
Por otra parte, la investigación fue dependiente de la disponibilidad de datos sobre las variables sujetas a estudio, los cuales ahora provienen de la PWT 9.0 (Feenstra et al., 2015). A partir de ello se realizaron diversos cálculos y transformaciones desde las series originales para construir las variables y series: Producto Interno Bruto real agregado por trabajador ocupado (ypt), y el stock de capital físico por trabajador ocupado (kpt), con un ajuste previo por capital humano sobre la base de años de escolaridad. A su vez, se realizaron transformaciones en las series obtenidas previamente, expresando logaritmos naturales y las primeras diferencias en los logaritmos con la finalidad de contar con una aproximación a las tasas de crecimiento de las variables sujetas a estudio.
Sin embargo, al tratarse de variables en series de tiempo, se procedió a determinar el orden de integración de las variables según las pruebas DickeyFuller aumentadas (ADF) y Phillips-Perron (PP) (Gujarati y Porter, 2010) mediante las rutinas de Eviews 10. En este sentido, los resultados obtenidos a través de las pruebas ADF y PP están recogidos en las Tablas 1 y 2.
Tabla 1 Pruebas de raíces unitarias Dickey-Fuller aumentad

a: Dickey-Fuller aumentado, utilizando el criterio de información de Schwarz para la selección de longitud de los rezagos, incluyendo términos:
CCST: Con constante, sin tendencia
CCCT: Con constante, con tendencia
SCST: Sin constante, sin tendencia
b: P-valores de una cola según MacKinnon (1996)
El término “Ln” que antecede a algunas de las variables hace referencia al logaritmo natural de la misma.
Las variables en minusculas “ypt” y “kpt” denotan al producto por trabajador y capital por trabajador respectivamente
Fuente: PWT versión 9.0, elaboración y cálculos propios sobre la base de Eviews 10.
Fuente: PWT versión 9.0, elaboración y cálculos propios sobre la base de Eviews 10.
Tabla 2 Pruebas de raíces unitarias Phillips-Perron
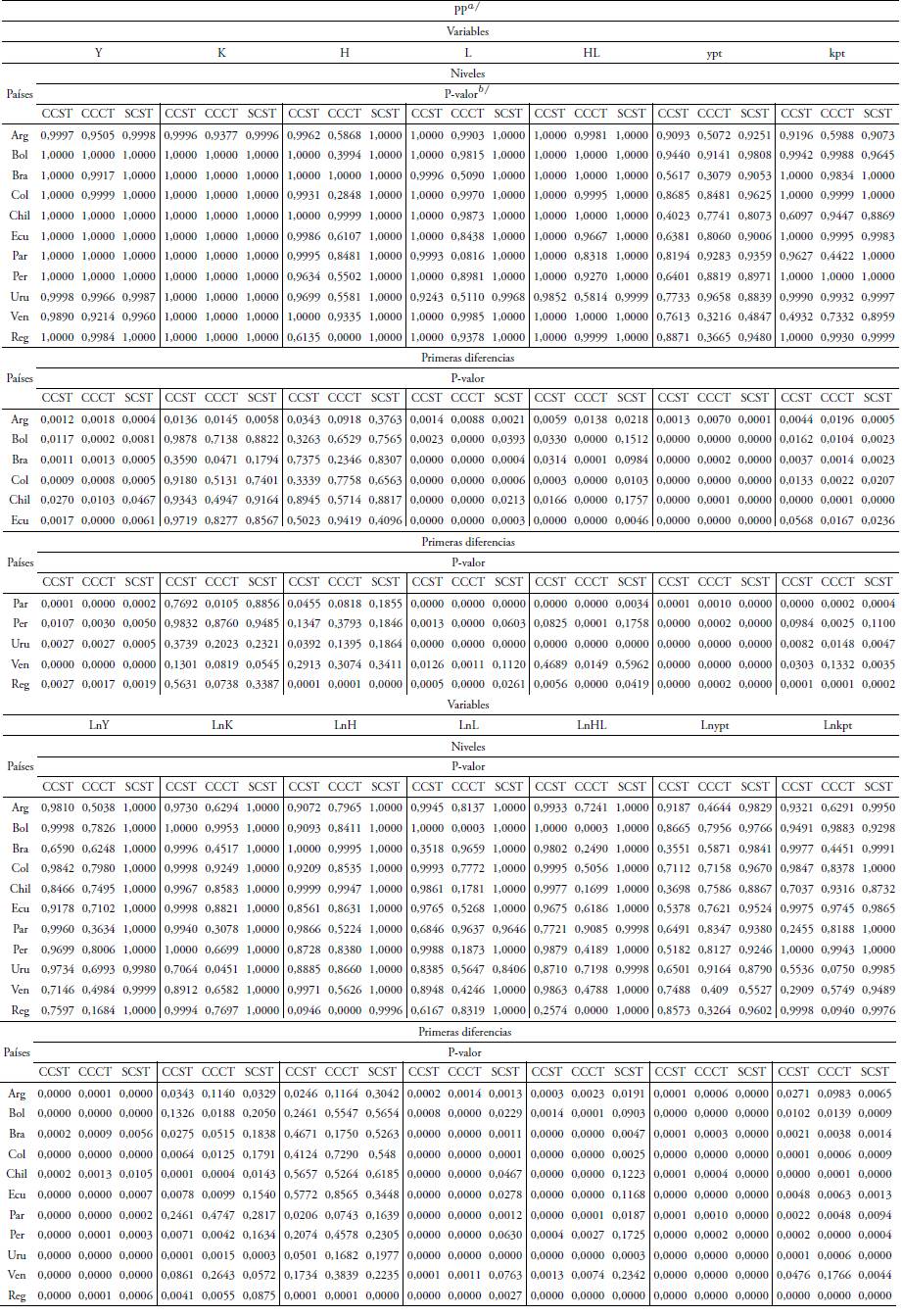
a: Phillips-Perron, utilizando el método de estimación espectral Bartlett Kernel y anchos de bandas Newey-West, incluyendo términos:
CCST: Con constante, sin tendencia
CCCT: Con constante, con tendencia
SCST: Sin constante, sin tendencia
b: P-valores de una cola según MacKinnon (1996)
El termino “Ln” que antecede a algunas de las variables hace referencia al logaritmo natural de la misma.
Las variables en minúsculas “ypt” y “kpt” denotan al producto por trabajador y capital por trabajador respectivamente
Fuente: PWT versión 9.0, elaboración y cálculos propios sobre la base de Eviews 10.
Los resultados demuestran que las variables observadas en niveles no rechazan la hipótesis nula de raíz unitaria dado los niveles de significancia estadística obtenidos, por lo cual es posible estimar el modelo con las variables en niveles si se cumple la condición de que los residuos estimados en la regresión sean estacionarios (Bejarano et al., 2018) de acuerdo con el enfoque de cointegración propuesto por Engle y Granger (Gujarati y Porter, 2010). Mientras que, en términos generales, las series observadas en primeras diferencias del logaritmo natural son estacionarias en su mayor parte con diversos niveles de significancia estadística que así lo demuestran.
Así mismo, las Tablas 3 y 4 presentan los resultados obtenidos mediante las estimaciones de la función de producción Cobb-Douglas intensiva con la inclusión de una medida de capital humano en los casos individuales de Argentina, Bolivia, Brasil, Chile, Colombia, Ecuador, Paraguay, Perú, Uruguay y Venezuela, así como también el total absoluto de la región de América del Sur en el período 1950-2014.
Cabe destacar que, desde el punto de vista estadístico, todos los residuos de las regresiones presentan una distribución normal acorde con los resultados de la prueba Jarque-Bera (Gujarati y Porter, 2010). Por otra parte, las series fueron previamente corregidas por posibles problemas de heterocedasticidad con el método de corrección de Newey-West (HAC) y, en algunos casos, se introdujo el esquema autorregresivo de primer orden AR(1) y las variables en diferencias para corregir posibles problemas de autocorrelación en los términos de error o residuos (Gujarati y Porter, 2010), situación que se ve reflejada en los resultados del estadístico Durbin-Watson de cada una de las regresiones.
Adicionalmente, se incluyeron en los casos de Bolivia, Colombia, Ecuador, Perú y Venezuela un término constante que registra el parámetro de la tecnología y una variable de tendencia para registrar el crecimiento de la función de producción que no está explicado por los factores productivos, lo cual se refleja en la Tabla 6. En el mismo orden de ideas, se incluyeron variables tipo dummy de impacto a causa de la posible presencia de quiebres estructurales en esos años particulares, originados por diversos factores de índole político, económico y social que pudieron haber generado cambios estructurales en las economías de la región. Las variables dummy demostraron ser estadísticamente significativas dentro de las regresiones en varios niveles de significancia (1 %, 5 % y 10 %).
Tabla 3 Resultados de las estimaciones de la función de producción intensiva con capital humano en el período (1950-2014a)
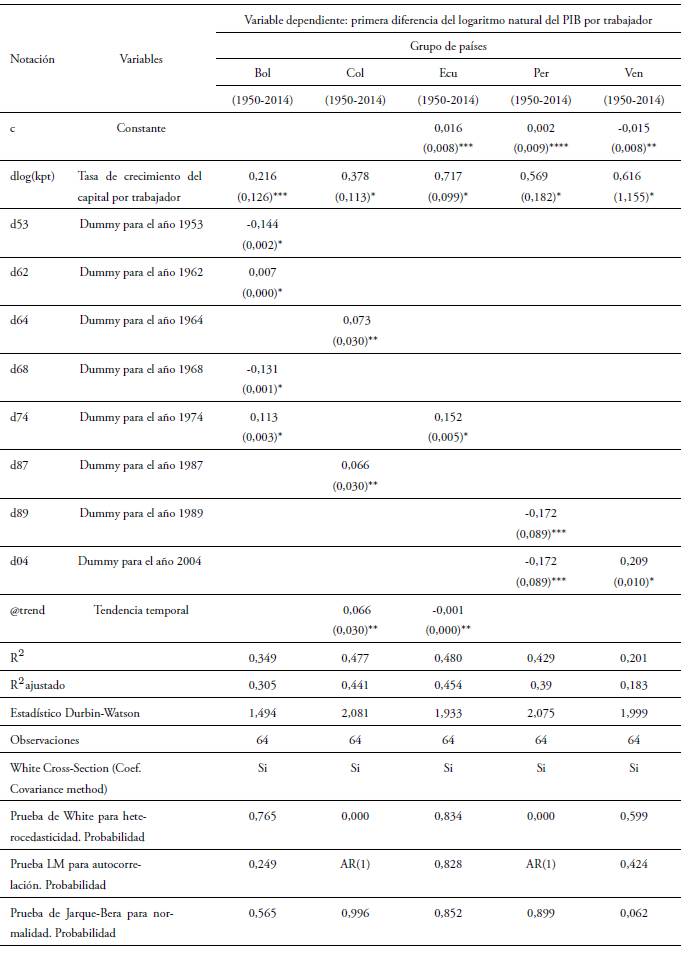
El log que antecede a la variable significa el logaritmo natural de dicha variable; una d delante de la variable significa la primera diferencia de dicha variable, mientras que cuando dlog antecede a una variable significa la primera diferencia del logaritmo natural de dicha variable (como aproximación de su tasa de crecimiento).
* Coeficientes significativos al 1 %, ** coeficientes significativos al 5 %, *** coeficientes significativos al 11 %, **** coeficientes nosignificativos. Errores estándar entre parentesis ().
Fuente: PWT versión 9.0, elaboración y cálculos propios sobre la base de Eviews 10.
Tabla 4 Resultados de las estimaciones de la función de producción intensiva con capital humano en el período (1950-2014b)

El log que antecede a la variable significa el logaritmo natural de dicha variable; una d delante de la variable significa la primera iferencia de dicha variable, mientras que cuando dlog antecede a una variable significa la primera diferencia del logaritmo natural de dicha variable (como aproximación de su tasa de crecimiento).
Coeficientes significativos al 1 %, ** coeficientes significativos al 5 %, *** coeficientes significativos al 11 %, **** coeficientes nosignificativos. Errores estándar entre parentesis ().
Fuente: PWT versión 9.0, elaboración y cálculos propios sobre la base de Eviews 10.
Dado los resultados en las regresiones efectuadas, se observa que las elasticidades del producto con respecto al capital por trabajador son en su mayoría consistentes con los supuestos de Mankiw et al. (1992), quienes argumentan que incluir el capital humano dentro del modelo de Solow (1956) tendría como resultado que la participación del capital físico y el crecimiento de la población tendrían un mayor impacto en los niveles del producto agregado o ingresos de la población.
En este sentido, al observar las elasticidades en los casos individuales de los países que conforman la región, estas sugieren que un aumento del 1 % en el stock de capital tiene como resultado un aumento del producto por trabajador, resultados que en su mayoría representan participaciones altas en el ingreso total de las economías por parte del factor capital por encima de la participación del factor trabajo, con excepción de los casos particulares de Bolivia y Colombia donde las elasticidades representan valores bajos para sostener dicha hipótesis.
Por otra parte, cuando se observa la elasticidad calculada para el agregado de la región (0,638), sugiere que un aumento del 1 % en el stock de capital tiene como resultado un aumento del 0,64 % en el producto por trabajador. Esto representa una participación alta en el ingreso total de la economía regional por parte del factor capital, que supera a la participación del factor trabajo.
Ahora bien, una de las limitaciones de las estimaciones realizadas es la moderada e incluso muy baja medida de bondad de ajuste de la regresión. Esto plantea la posibilidad de que pueden existir factores no incorporados dentro del modelo en forma de elementos o variables exógenas no especificadas dentro de la forma funcional del mismo.
IV. Análisis de la productividad total de los factores en la región de América del Sur
Una vez obtenidas las elasticidades en la función de producción CobbDouglas intensiva, se procedió a estimar la tasa de crecimiento de la PTF para la región de América del Sur y sus países integrantes a través de la metodología de la contabilidad del crecimiento establecida por Solow (1957).
En este sentido, la Tabla 5 recopila los resultados hallados en conjunto a la descomposición de la experiencia del crecimiento económico en la región y cada uno de los países que la conforman.
Tabla 5 Descomposición del crecimiento económico en América del Sur. Período (1950-2014)

Fuente: PWT versión 9.0, elaboración y cálculos propios sobre la base de Eviews 10.
Estos resultados demuestran que en el período 1951-2014, el PIB real creció a una tasa promedio en el rango de entre 2,55 % en el punto más bajo correspondiente a Uruguay y 5,52 % en su punto más alto correspondiente a Brasil, mientras los demás países muestran valores similares en el rango de entre 4,05 y 5,01 %. El stock de capital tuvo un rendimiento similar con una tasa de crecimiento promedio en el rango de 4,01 % en su punto más bajo correspondiente a Bolivia y 6,27 % en su punto más alto de nuevo correspondiente a Brasil, mientras que los demás países muestran valores similares en el rango de 4,10 % y 6,20 %.
El factor trabajo (ajustado por un índice de capital humano sobre la base de años de escolaridad) muestra una tasa de crecimiento promedio menor al factor capital en el rango de 1,84 % en su punto más bajo correspondiente a Uruguay y 4,42 % en su punto más alto correspondiente a Venezuela, mientras los demás países presentan un rango de valores similares en el rango de 2,34 % a 3,80 %.
Mientras tanto, la PTF demostró resultados poco favorables en un espectro negativo en cuanto a su tasa de crecimiento promedio se refiere, situándose en un rango de -1,16 % en su punto más alto correspondiente a Venezuela y -0,04 % en su punto más bajo correspondiente a Argentina, con la excepción de países como Bolivia, Brasil, Chile y Ecuador con un promedio de 0,79 %, 0,10 %, 0,43 % y 0,06 %, respectivamente. Por otra parte, al analizar los resultados del total absoluto de la región se puede observar que el PIB real creció a un promedio de 4,98 %, el stock de capital en 5,82 %, el factor trabajo en 2,60 % y la PTF en un -0,16 %. En este contexto los resultados revelan que, en cuanto a la experiencia del crecimiento de América del Sur, la principal fuente del crecimiento del producto ha sido la acumulación de factores productivos más que la productividad total, lo cual puede comprobarse más a fondo observando la Figura 1 y la Tabla 6.
En la Figura 1 se puede observar que el crecimiento de la PTF en la región a lo largo del período fue altamente inestable, mientras que la acumulación de factores demostró ser más estable, lo cual en conjunto a las estimaciones de la participación de la productividad en el crecimiento promedio del producto (Tabla 6) y la descomposición previa del crecimiento (Tabla 5), revela que existen factores adicionales a tomar en cuenta para explicar las variaciones en el crecimiento regional (Easterly y Levine 2001) debido a que, la productividad no ha sido determinante en cuanto al crecimiento económico de Suramérica en el período 1950-2014, demostrando que la región es altamente ineficiente a la hora de combinar y emplear sus factores productivos, lo que en alguna medida determinó el desempeño económico de la misma especialmente durante los episodios de decrecimiento e inestabilidad económica del siglo XX (Solimano y Soto, 2005), y los que le proseguirían en la primera parte del siglo XXI.
Tabla 6 Porcentaje del crecimiento promedio del PIB correspondiente al crecimiento de la PTF. Período (1950-2014)
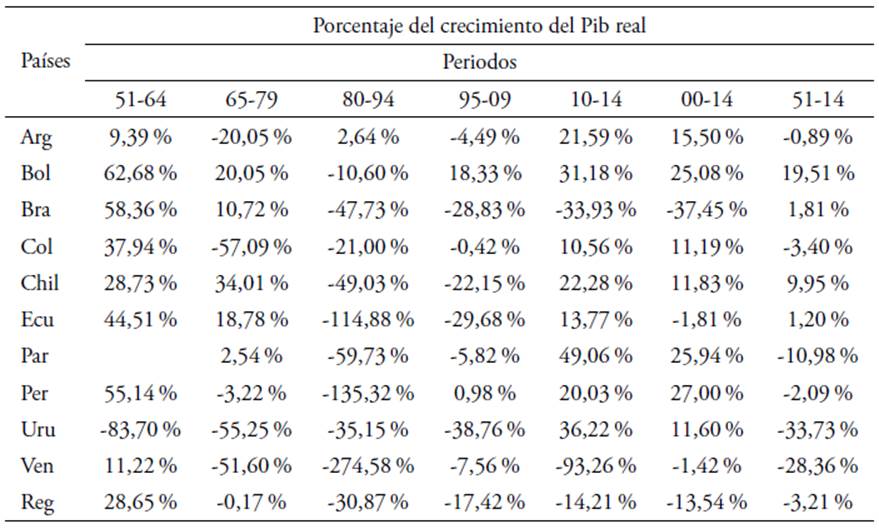
Fuente: elaboración y cálculos propios a partir de los resultados de la Tabla 5.
Dentro de este contexto, cabe descartar que estas conclusiones son consistentes con los hallazgos de trabajos a menor escala dentro de economías específicas de la región como los de Mora (2006), Puente et al. (2010), Bejarano et al. (2018), Briones et al. (2018), y aquellos a escala de mayor que toman en cuenta toda América Latina como los de Solimano y Soto (2005), Méndez-Sayago et al. (2013) y Araujo y et al. (2014). Al igual que trabajos con muestras a nivel internacional como los de Easterly y Levine (2001), Canarella y Pollard (2003) y Koutun y Karabona (2013), cuyos objetivos fueron comprobar la validez empírica del modelo MRW (1992), obteniendo resultados positivos en el proceso.

Fuente: PWT versión 9.0, elaboración y cálculos propios sobre la base de Eviews 10
Figura 1 Comportamiento de la Productividad total de los factores en América del Sur. Período (1950-2014)
Una interesante área de estudio ampliamente documentada y con referentes empíricos es sobre los determinantes a corto y largo plazo de la PTF, cuestión que se sugiere investigar para el caso de los países estudiados, en cuanto permitiría tener referencias más exactas sobre las causas por las cuales esta región tiene dificultades respecto a la expansión de su productividad total.
Conclusiones
La teoría del crecimiento económico exógeno predice que los países pobres deberían crecer a un ritmo más rápido que los países ricos lo cual permitiría que haya convergencia a nivel de sus ingresos per cápita. La evidencia empírica disponible revela que, en la última mitad del siglo XX, muchas economías de diferentes regiones como Europa del Sur, Europa Occidental y Asia del Este, efectivamente disfrutaron de importantes experiencias de crecimiento económico logrando reducir significativamente sus brechas de ingresos y niveles de desarrollo en comparación a otras naciones (Acemoglu, 2009).
Según los resultados obtenidos por medio de las regresiones formalizadas en la función de producción Cobb-Douglas en términos intensivos, se puede concluir que las elasticidades del producto con respecto al factor capital son, mayoritariamente, consistentes con los supuestos del modelo Solow-Swan ampliado de Mankiw et al. (1992). Estos autores señalan que incluir el capital humano dentro del modelo de Solow (1956) tendría como resultado evidencia más acorde a la pauta de distribución del ingreso, donde el capital en un sentido amplio tiene mayor participación en el producto total de la economía.
No obstante, si bien el modelo econométrico fue bien especificado y se obtuvieron estimaciones consistentes, los estadísticos que representan la bondad de ajuste de la ecuación de regresión demostraron ser valores mediobajos, por lo que se concluye que pueden existir factores que participan a la hora de determinar el rendimiento económico de América del Sur y sus países miembros, que no están siendo registrados dentro del modelo, como por ejemplo la estructura institucional de la región y el funcionamiento de la misma en ella, que como lo demuestra la evidencia empírica disponible las instituciones pueden ser determinantes en el desempeño económico de largo plazo de las naciones (Acemoglu, 2009; Acemoglu y Robinson, 2012). Por lo que se recomienda expandir el modelo para remediar dicha situación y encontrar resultados más concluyentes al respecto.
Por su parte, los resultados del objetivo general de la investigación evidencian que la principal fuente del crecimiento en el producto total en la región fue la acumulación de factores productivos más que la productividad total de la misma, que no ha sido un factor determinante del crecimiento en el período de estudio 1950-2014, por lo cual la región es ineficiente a la hora de emplear y combinar sus factores productivos en comparación con otras regiones del mundo. Algo que ha jugado un factor determinante en el desempeño económico de largo plazo de Suramérica, especialmente cuando se toma en cuenta los posibles efectos adversos de esta ineficiencia durante los episodios de inestabilidad macroeconómica como consecuencia de choques exógenos y desequilibrios internos.
Por último, se destaca que los resultados invitan, como siempre es el caso en las investigaciones empíricas, a atender la calidad de la data, dada la importancia de tomar en cuenta los cambios que tienen lugar a lo largo del tiempo en la recolección y medición de las cuentas nacionales de los distintos países estudiados, al igual que una gran parte de la investigación sobre el capital humano y crecimiento económico debe ser reexaminada debido a la disponibilidad de nuevas o actualizadas fuentes de datos macroeconómicos (Canarella y Pollar, 2003).