Introducción
Los instrumentos derivados clásicos -como futuros y opciones- han sido utilizados para valorar y resolver problemas de cobertura sobre numerosos activos subyacentes. Sin embargo, frente a algunas situaciones complejas y controvertidas de determinados activos, tales herramientas muestran limitaciones por su rigidez. En este contexto, adquieren relevancia los instrumentos exóticos, que superan los límites de las operaciones estándar al admitir mayor flexibilidad sobre algunas reglas del contrato para ajustarse a determinadas circunstancias, abaratar el costo de las primas respecto de las opciones tradicionales y cambiar la estructura de pagos (Crespo, 1998; García et al., 2000).
Las opciones exóticas, también conocidas como de segunda y tercera generación, difieren de las clásicas o vainilla, ya sea por la determinación del precio de ejercicio, el precio del activo subyacente, la prima, las condiciones de pago, el número de subyacentes, entre otros (Crespo, 1998). Este tipo de instrumentos se diseña a partir de la modificación de ciertas condiciones del contrato de una opción vainilla y su origen ha sido incentivado por la búsqueda de mejoras en los procesos de administración de riesgos en un contexto de volatilidad creciente en los mercados, los avances tecnológicos y el fuerte desarrollo de la teoría de valoración de opciones (García et al., 2000).
Si bien el uso de derivados exóticos en los mercados se ha acrecentado en las últimas décadas, su volumen de negociación todavía es escaso en términos relativos en comparación a los contratos tradicionales, excepto en el mercado energético donde su desarrollo ha sido más vasto (CME Group, 2020). Entre los motivos que explican la aun baja utilización de estos instrumentos se destacan: el desconocimiento de este tipo de contratos, la reducida oferta en el mercado por parte de instituciones financieras, la dificultad de establecer el valor de las primas y la baja contribución que se ha realizado desde el ámbito académico para comprender sus ventajas (Crespo, 2001).
Dos décadas despues de las ideas expresadadas en el párrafo precedente, cabe debatir qué contribuciones se realizaron para revertir esta debilidad en la adopción de este tipo de instrumentos. Si bien se reconocen textos académicos que conceptualizan algunos tipos de opciones exóticas (Cortés, 2019; Crespo, 2001; García et al., 2000; Mascareñas, 2013; Ripio & Carranza, 2009; Zhang, 1995), no se identifican revisiones sistemáticas sobre el tema que indaguen la importancia y el enfoque brindado a tales instrumentos exóticos en la literatura.
En este orden de ideas, el presente artículo aborda la brecha detectada al desarrollar un análisis conceptual de la literatura académica sobre opciones exóticas. En particular, se plantean los siguientes objetivos específicos (OE):
i. describir los principales conceptos sobre opciones exóticas, su tipificación y características principales (OE1); y ii. analizar la evolución de las publicaciones en la temática mediante una revisión sistemática de la literatura en las principales bases de datos académicas (OE2).
Para abordar los objetivos propuestos, metodológicamente, se desarrolla un estudio de alcance exploratorio-descriptivo a partir de un análisis documental de publicaciones de autores clásicos para atender el OE1 y de una revisión sistemática para alcanzar el OE2. Las revisiones sistemáticas de literatura se identifican como un procedimiento riguroso de relevamiento conceptual que permiten identificar publicaciones notables y detectar brechas de conocimiento, tensiones entre la teoría y la práctica o controversias de resultados empíricos dentro de la academia (Manterola et al., 2013). En este artículo, la búsqueda bajo protocolo se efectúa en las bases de datos Scopus y Web of Science, y las publicaciones resultantes se someten a dos análisis: bibliométrico y de contenido.
La relevancia del artículo está dada tanto por sus contribuciones académicas como por sus implicancias prácticas. A nivel teórico, el trabajo desarrolla un compendio conceptual sobre estos instrumentos exóticos, que resulta de utilidad para realizar una inmersión en la temática. Además, presenta un análisis de la evolución de la literatura de las principales bases académicas mundiales, mediante la caracterización de un extenso conjunto de publicaciones referidas a opciones exóticas, que permite detectar tipologías más y menos estudiadas, así como temas candentes de los últimos años. Asimismo, representa un cimiento sustancial para futuros estudios empíricos pues permite individualizar las publicaciones de mayor relevancia sobre derivados exóticos.
Como implicancias prácticas, es esperable que la difusión y el aporte para esclarecer la comprensión del tema deriven en una mayor utilización de los instrumentos exóticos en los mercados, a fin de aprovechar sus menores primas -en algunos casos- y las condiciones más ajustadas a situaciones reales provocando coberturas eficientes, así como adoptar su uso para otro tipo de activos o situaciones complejas y controvertidas donde se requiere flexibilidad sobre ciertas reglas del contrato.
Luego del presente apartado introductorio, el artículo se estructura de la siguiente manera. El acápite I presenta la conceptualización y clasificación de las principales opciones exóticas. El apartado II detalla el protocolo de revisión sistemática y otros aspectos metodológicos. La sección III exhibe los resultados de la revisión de literatura, organizados en dos subsecciones: bibliométrica y de contenido. Finalmente, en las conclusiones se sintetizan y discuten los hallazgos.
I. Conceptualización y clasificación
A partir de un análisis documental de textos de autores clásicos sobre instrumentos derivados (Crespo, 2001; Fernández & Ariño, 1996; García et al., 2000; Hull, 2002; Kolb, 2003, 2011; Mascareñas, 2013), se realiza en esta sección una conceptualización y tipificación de opciones exóticas, que abarca un conjunto amplio de contratos al reorganizar y sistematizar información proveniente de diversas fuentes. El apartado presenta inicialmente conceptos generales, para ubicar las opciones exóticas dentro de las familias de derivados y luego se profundiza sobre cada tipología.
Existen diferentes familias de opciones según el criterio analizado (Figura 1). De acuerdo con el comportamiento de los pagos -y, por lo tanto, el valor del contrato derivado- las opciones pueden ser tradicionales -o vainilla- o bien, exóticas. Según el tiempo para su ejercicio, pueden ser americanas, si el derecho que otorgan se puede ejercer hasta su vencimiento, o europeas, cuando solo puede ejercerse al vencimiento. Finalmente, considerando el activo subyacente, se puede tratar de opciones financieras si tienen mercado de cotización y activos con negociación, o reales cuando el subyacente está vinculado a proyectos de inversión y, por ende, no tienen mercado.
Las opciones exóticas son un tipo de instrumento derivado que presenta modificaciones en la estructura de resultados y, por lo tanto, en la matriz de pagos, producto de cambios sobre las reglas del contrato respecto a los derivados tradicionales (Fernández & Ariño, 1996; García et al., 2000; Hull, 2002; Kolb, 2003). Estas características les otorgan mayor flexibilidad a dichos contratos, tornándolos atractivos y permitiéndoles adaptarse a situaciones diversas, pero su valoración se ha convertido en un problema complejo con amplio desarrollo analítico.
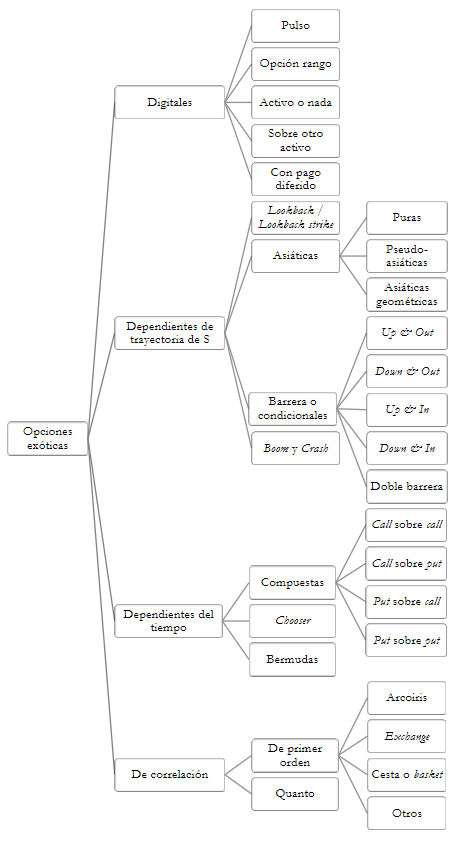
Dentro del diverso conjunto de derivados exóticos1, se puede mencionar, a modo de ejemplo, opciones compuestas, digitales, chooser, barrera, lookback, asiáticas, arcoíris, entre otras. La mayoría de estos instrumentos exóticos se negocian en el mercado over-the-counter. La Figura 2 exhibe los principales tipos de opciones exóticas2 agrupados por familias. La descripción de tales opciones se presenta en las secciones siguientes y se resume esquemáticamente en la Tabla 1.
A. Familia de opciones digitales
Las opciones digitales o binarias tienen pagos y rendimientos discontinuos, determinados por el hecho de que el precio del subyacente (S) termine por debajo o por encima del precio de ejercicio (X), recibiendo nada o la totalidad de un monto fijo establecido en cada caso. Dentro de esta familia se distinguen:
Las opciones digitales puras o pulso, también conocidas como cash or nothing. Son binarias con un pago total o nulo de acuerdo si sucede el evento. Esto es, por ejemplo, para el tenedor de una opción call, en la fecha de vencimiento recibe un monto fijo P si S ≥ X o 0 si S < X, pero X nunca es pagado. Este tipo de opciones digitales son utilizadas de manera experimental para mercado de eventos, como atentados terroristas, resultados deportivos, éxito de una película, elecciones políticas, opiniones de mercado, entre otros.
Las opciones rango activan el pago fijo si el precio del subyacente pertenece a un intervalo determinado por dos precios de ejercicio: X1 < S < X2. En caso contrario el pago es nulo.
En las opciones binarias conocidas como activo o nada (asset-or-nothing). El tenedor recibe el activo en caso de estar dentro del dinero, independientemente de si se trata de un call o un put. Por supuesto, cambia la zona de precios para los cuales la opción estará in-the-money (S > X para call y S < X para put ).
Las opciones sobre otro activo permiten obtener o vender un activo A a determinado precio, si el precio de otro activo B es superior/inferior a X. Suelen utilizarse para ofertas de intercambio de acciones en una adquisición de firmas, arreglo de honorarios, ofertas de intercambio, entre otras.
En las opciones con pago diferido el tenedor no abona nada hoy y solo debe abonar la prima en caso de ejercicio. Por ejemplo, para el comprador de una opción call con pago diferido, al momento del ejercicio obtendrá S − X − c si S ≥ X ó 0 en caso contrario. Fernández & Ariño (1996) indican que el ejercicio es obligado para el comprador en situaciones en las que naturalmente no ejercería, por ejemplo, en un call cuando el precio del subyacente no es superior a X − c.
B. Familia de opciones dependientes de la trayectoria de S (path-dependent)
En las opciones dependientes de la trayectoria del precio del activo subyacente, el ejercicio del derecho que otorga la opción y su matriz de pago dependen, no solo del valor de S al final de la vida del contrato o en algún momento de la misma, sino de su evolución durante ese plazo temporal. Dentro de esta amplia familia de opciones, se identifican los tipos lookback o loockback strike, asiáticas o de precio medio, barrera o condicionales, boom y crash, entre otras.
Los pagos de las opciones lookback dependen del precio máximo o mínimo alcanzado por el subyacente durante la vida de la opción y no meramente del valor final del mismo al momento de expiración del derecho a ejercicio. También existen lookback strike, que son opciones en las que el precio de ejercicio es determinado por el valor máximo o mínimo que alcanza el precio del subyacente. Estas opciones siempre se ejercen por la definición de X. En términos generales, las opciones lookback presentan primas superiores a las tradicionales.
Las opciones asiáticas son aquellas cuyos pagos dependen del precio medio del subyacente, tanto en el rol del subyacente propiamente dicho, como en el rol del precio de ejercicio. A partir de esta cuestión se distinguen: 1) opciones asiáticas puras, en las que el valor del subyacente se sustituye por el valor medio del subyacente durante la vida del contrato (o una parte de ella); 2) opciones pseudo asiáticas, en las que X se sustituye por el valor medio del subyacente; y 3) opciones asiáticas geométricas, en donde se trabaja con medias geométricas para sustituir S o X. Este tipo de opciones reduce la posibilidad de manipular los precios de los activos subyacentes para obtener mayores pagos al momento del ejercicio de la opción.
Las opciones barrera o condicionales son aquellas en las cuales el ejercicio depende de si el precio del subyacente alcanza cierto nivel durante un período de tiempo determinado. La barrera puede ser inferior o superior al precio de ejercicio. Si el nivel fijado como barrera es superior, se trata de opciones up y de ser inferior, down. Las opciones que entran en ejercicio al alcanzar la barrera se denominan knock in, mientras que aquellas que desvanecen el derecho de ejercicio al llegar a la barrera son las knock out. Las opciones in se convierten en vainilla una vez tocada la barrera, mientras que las out son tradicionales hasta alcanzarse la barrera, en donde el derecho se desvanece.
De la descripción anterior surgen cuatro combinaciones posibles: up & in, down & in, up & out, down & out, presentadas en la Figura 3. Existe una quinta clase dentro de esta familia de opciones que se presenta cuando el derecho desaparece en caso de que el activo subyacente no permanezca dentro de un rango determinado fijado por una doble barrera.
Dado que las barreras son opciones tradicionales sujetas a una condición valen menos que las opciones vainilla, sin condiciones. Ciertas opciones barrera tienen un “premio consuelo” que se paga en una opción out cuando se alcanza la barrera, y en una in cuando la opción expira y no se alcanzó la barrera.
Las opciones boom y crash tienen como precio de ejercicio y del activo subyacente una rentabilidad, por lo que luego se lo transforma en unidades monetarias mediante un valor nocional (VN) (Fernández & Ariño, 1996). El método de valoración utilizado suele ser el de martingalas. En particular:
C. Opciones exóticas con reglas dependientes del tiempo
En este apartado se describen algunas opciones con reglas de ejercicio y pagos dependientes del tiempo durante la vida del contrato, en las que, en cierto momento futuro, la rentabilidad se vincula al valor de una opción vainilla. Dentro de este subconjunto, se destacan las opciones compuestas, chooser y Bermuda.
Las opciones compuestas o anidadas son opciones en las que el activo subyacente es otra opción, por lo que tienen dos precios de ejercicio y dos fechas de vencimiento. Existen cuatro combinaciones posibles: call sobre call, call sobre put, put sobre call y put sobre put. Según García et al. (2000), este tipo de opciones se suele utilizar para la cobertura de riesgos con baja probabilidad de ocurrencia, por lo que suponen coberturas condicionales. Por ejemplo, una opción call sobre una put da a su comprador el derecho de comprar un put. Si en la primera fecha de vencimiento se ejerce el derecho, se paga el primer X y se recibe una put, que le dará el derecho a vender el activo subyacente a un segundo X en la segunda fecha de vencimiento.
Las opciones chooser tienen la particularidad de que luego de un período de tiempo determinado, el comprador puede decidir si se trata de una opción de compra o de venta, con igual o diferente precio de ejercicio y vencimiento, condiciones establecidas al momento de emitir la opción. A posteriori de la fecha en la que caduca la elección, la opción resultante es un call o put vainilla o tradicional, pero la dificultad se presenta para valorar la opción antes de la fecha de elección, por tener un derecho adicional. Suele utilizarse cuando existe incertidumbre sobre un cambio de política que puede afectar la dirección de la tendencia de S.
Las opciones bermuda plantean una novedad en cuanto al momento del ejercicio, pudiendo ser ejercidas de forma anticipada en determinadas fechas antes del vencimiento. De este modo constituyen un híbrido entre las opciones europeas y las americanas.
D. Opciones exóticas de correlación
En las opciones dependientes de la correlación, su estructura de pago deriva de más de un activo subyacente y su correlación es determinante tanto de su valor, así como de la estrategia de cobertura. Existen distintas modalidades para este tipo de opciones, las que se agrupan en: 1) opciones con correlación de primer orden: su valor depende directamente de la correlación entre los distintos activos subyacentes; y 2) opciones con correlación de segundo orden: se trata de opciones denominadas sobre una moneda que generan rendimientos en otra moneda. Dentro de la familia de opciones con correlación de primer orden, se destacan las conocidas como arcoíris, de intercambio, cesta, entre otras.
Las opciones arcoíris permiten combinar pagos entre un conjunto de activos, al generar su resultado de acuerdo con los rendimientos obtenidos por los activos subyacentes de la opción. Se suelen llamar arcoíris de n colores, siendo n el número de activos riesgosos que se pueden intercambiar. Dentro de este tipo, se despliega el siguiente abanico de alternativas:
El máximo entre un set de activos riesgosos: en caso de ejercicio, por ejemplo, en un call, el comprador paga X y recibe el activo con mayor valor. Por lo que el valor intrínseco se presenta como máx(máx(S1, S2, . . . ,Sn) − X <;0) para un call y máx(X − máx(S1,S2, . . . ,Sn); 0) para un put.
El mejor entre un set de activos riesgosos: es un caso particular del anterior. Otorgan al comprador el mejor de los activos, pero a diferencia del caso anterior X es cero en este caso.
El mejor entre un set de activos y un monto de fijo de dinero: dado que existen n + 1 payoffs posibles, no hay X en este tipo de opciones.
El mínimo de un set de activos riesgosos: en caso de ejercicio, por ejemplo, en un call, el comprador paga X y recibe el activo con menor valor. Por lo que el valor intrínseco se presenta como máx(mín(S1,S2, . . . , Sn) − X; 0) para un call y máx(X − mín(S1,S2, . . . ,Sn); 0) para un put. Claramente presentan una prima mucho menor.
El peor de un set de activos riesgosos: otorgan al comprador el peor de los activos, pero a diferencia del caso anterior X es cero en este caso.
Entre las opciones con correlación de primer orden también se encuentran:
Exchange o de intercambio: el propietario puede decidir cambiar un activo por otro.
Opciones cestas (basket): dan el derecho a comprar o vender una cesta o cartera de activos, contra una divisa base.
Sobre diferenciales: S se sustituye por el diferencial entre dos parámetros. El valor intrínseco al vencimiento es el máx((Sn1 − Sn2) − X; 0) para un call y máx(X − (Sn1 − Sn2); 0) para un put.
Dual strike: opciones sobre el mejor de dos valores intrínsecos al vencimiento de dos activos con precios de ejercicio diferentes.
Entre las opciones exóticas con correlación de segundo orden, se destacan las quanto, que son opciones que generan un pago en una moneda diferente a la denominada de acuerdo con el activo subyacente del contrato. Este tipo de opciones permite aislar riesgos asociados al tipo de cambio.
II. Protocolo de revisión y metodología
Una revisión sistemática es una síntesis de la evidencia disponible, en la cual se realiza un examen de aspectos cuantitativos y cualitativos de estudios primarios, con el objetivo de resumir la información existente respecto de un tema en particular (Manterola et al., 2013). Se trata de un tipo de investigación científica que reúne varios estudios originales, resumiendo los resultados a través de estrategias que limitan los sesgos y los errores aleatorios. Las revisiones sistemáticas de calidad pueden establecer los límites entre lo conocido y desconocido sobre una temática determinada (Cook et al., 1997) y limitar tanto sesgos personales como errores aleatorios (American Psychological Association [APA], 2010).
El procedimiento consiste en definir los criterios de búsqueda apropiados para la revisión, recolectar los artículos vinculados y proceder a un análisis de los metadatos. Este tipo de estudios tiene la positiva particularidad de contar con un protocolo explícito que permite replicar la búsqueda realizada en otros momentos de tiempo o por otros investigadores. En ese sentido, una revisión sistemática implica un proceso transparente, explícito, reproducible y con mínimo sesgo por parte del autor, respetando el rigor científico (Janissek et al., 2015).
Con relación a los criterios de búsqueda, considerando el objetivo propuesto en este artículo, se realizó durante el mes de marzo de 2020 una revisión sistemática de la literatura sobre opciones exóticas en las bases de datos Scopus y Web of Science (WOS) con los términos exhibidos en la Figura 4 dentro del campo “título”. Las mencionadas bases se seleccionaron por tratarse de repositorios de fuentes internacionales de alto impacto académico, con herramientas de búsqueda avanzada y posibilidad de exportación de registros.
El primer conjunto de resultados fue depurado excluyendo aquellos trabajos que no estuvieran en español, inglés o portugués. Luego, los hallazgos filtrados se exportaron y tabularon en una planilla de cálculo. Después de comparar los ítems entre las bases de datos, se totalizaron 99 artículos, 59 de los cuales se encuentran tanto en WOS como en Scopus (Figura 4).
Posteriormente, se procedió a la lectura de los títulos y resúmenes de las 99 publicaciones a fin de identificar sus principales características, las cuales se exponen en la Tabla A1 del anexo: autor(es); fecha; tipo de fuente; número de citas total y por año; propuesta y objetivo del estudio, resultados y contribución del trabajo, abordaje (teórico, empírico, teórico-empírico), y tipo de opción(es) exótica(s) usada(s). Durante el proceso de tabulación de los resultados se eliminaron tres registros3, por lo que la Tabla A1 del anexo quedó integrada por 96 publicaciones.
Las publicaciones obtenidas como resultado del proceso descripto se sometieron a dos tipos de análisis: bibliométrico y de contenido, los cuales se exponen en las subsecciones A y B del apartado III. El análisis bibliométrico busca determinar la cantidad de trabajos publicados sobre determinado tema y sus características como autores, número de citas, fuente, tipo de publicación (APA, 2010). El propósito del análisis bibliométrico es catalogar, clasificar y cuantificar los conocimientos de una disciplina (Ferreira, Storopoli et al., 2014). Si bien la bibliometría es una técnica antigua (Ferreira, Cardoso et al., 2013), la actual existencia de distintas bases de datos dedicadas a la catalogación de producción científica le otorga mayor relevancia al análisis estadístico de las publicaciones (Santos, 2012).
En segunda instancia, se aplicó un análisis de contenido que, según Bardin (2011), comprende tres fases principales: preanálisis; exploración; y tratamiento e interpretación de resultados. El preanálisis de los datos mediante la examinación de las publicaciones permite identificar ideas generales, temas emergentes y puntos clave, y definir tópicos que se repiten con mayor frecuencia. En la fase de exploración se procede a codificar los datos y surgen categorías temáticas para su clasificación. En la última etapa se procede a su tratamiento e interpretación mediante una inmersión profunda, a fin de dar validez y significatividad a la información (Bardin, 2011). Para la generación de nubes de palabras del análisis de contenido se empleó como herramienta auxiliar el software Voyant Tools4.
III. Estado del arte
A. Análisis bibliométrico
El Anexo A.1 sintetiza las principales características de los 96 estudios considerados y, en los párrafos siguientes, se comentan los aspectos bibliométricos generales del conjunto analizado. Respecto al tipo de fuente (Tabla 2), los resultados provienen mayoritariamente de revistas y en menor medida de congresos y libros. Asimismo, las publicaciones no se encuentran atomizadas, sino que se observa una diversidad de revistas. Solo seis revistas tienen más de una publicación sobre el tema, entre las que se destaca la participación del Journal of Mathematical Finance. Dicha variedad también se observa en las publicaciones provenientes de eventos científicos, donde el único que aporta más de un trabajo es el International Conference on Computational Science.
La tendencia temporal de los resultados (Tabla 3, Figura 5) se extiende de 1995 a 2019 con forma de parábola (solo en 1996 no existe ninguna publicación): la primera década muestra un número incipiente de publicaciones; la mayoría de los resultados (63,54 %) se ubica entre 2006 y 2015 y, finalmente, se observa una caída del número de artículos para el lapso 2015-2019. Este decrecimiento puede deberse -además del menor rango temporal considerado- a la demora inherente a la accesibilidad de las publicaciones de los últimos años. El 2013 se destaca por presentar mayor cantidad de trabajos en el tema.
Tabla 3 Publicaciones por quinquenio y por año
| Rango | N° resultados | Año | Nº resultados | Año | Nº resultados |
|---|---|---|---|---|---|
| 1995-2000 | 8 | 2006 | 6 | 2011 | 5 |
| 2001-2005 | 12 | 2007 | 8 | 2012 | 6 |
| 2006-2010 | 32 | 2008 | 3 | 2013 | 10 |
| 2011-2015 | 29 | 2009 | 8 | 2014 | 2 |
| 2016-2019 | 15 | 2010 | 7 | 2015 | 6 |
| 96 | 32 | 29 | |||
Fuente: elaboración propia.
Según la cantidad de citas totales (Tabla 4), existen tres publicaciones seminales y nueve trabajos que presentan entre 16 y 30 citas, los que representan un 12,50 % del total de publicaciones analizadas. Luego hay 52 trabajos con el rango de 1 a 15 citas (54,17 %) y 32 con ninguna referencia externa (33,33 %).
Tabla 4 Publicaciones más citadas (términos absolutos)
| Nº citas (valor o rango) | Nº resultados | Frecuencia relativa | Frecuencia acumulada | Referencias |
|---|---|---|---|---|
| 116 | 1 | 1,04 % | 1,04 % | Carr et al. (1998) |
| 75 | 1 | 1,04 % | 2,08 % | Boyle & Draviam (2007) |
| 47 | 1 | 1,04 % | 3,13 % | Kamat & Oren (2002) |
| 26-30 | 3 | 3,13 % | 6,25 % | Beaglehole et al. (1997); Chen, Deelstra et al. (2008); Guo & Shepp (2001) |
| 21-25 | 3 | 3,13 % | 9,38 % | Detlefsen & Härdle (2007); Lasserre et al. (2006); Lin (1998) |
| 16-20 | 3 | 3,13 % | 12,50 % | Ching et al. (2007); Khaliq et al. (2007); Schoutens (2006) |
| 11-15 | 10 | 10,42 % | 22,92 % | |
| 6-10 | 11 | 11,46 % | 34,38 % | |
| 1-5 | 31 | 32,29 % | 66,67 % | |
| 0 | 32 | 33,33 % | 100,00 % | |
| Total | 96 | 100,00 % | 100,00 % |
Fuente: elaboración propia.
Por su parte, cuando se considera la cantidad de citas por año, los artículos más relevantes resultan ser los expuestos en la Tabla 5. Si bien varios trabajos coinciden con los más citados en términos absolutos, también surge una serie de investigaciones recientes que ha logrado un buen impacto en la academia (filas sombreadas Tabla 5).
Tabla 5 Publicaciones más citadas (términos relativos)
| N° citas por años | Resultados |
|---|---|
| 6,25 | Boyle & Draviam (2007) |
| 6,00 | Bormetti, Callegaro et al. (2018) |
| 5,52 | Carr et al. (1998) |
| 5,00 | Fusai et al. (2016) |
| 3,00 | Hieber (2018) |
| 2,76 | Kamat & Oren (2002) |
| 2,27 | Chen, Deelstra et al. (2008) |
| 1,75 | Detlefsen & Härdle (2007) |
| 1,63 | Basak et al. (2011) |
| 1,62 | Lasserre et al. (2006) |
| 1,60 | Lipton et al. (2014) |
| 1,58 | Khaliq, Voss & Yousuf (2007) |
Fuente: Elaboración propia
Al analizar la autoría de las publicaciones (Tabla 6), también se observa diversidad. Schoutens es el autor más frecuente, participando en cuatro trabajos; seguido por Bornetti, Li, Zhang y Zhou, quienes participan en tres publicaciones cada uno. Los restantes autores de la Tabla 6 cuentan con dos artículos per cápita.
B. Análisis de contenido
Para el análisis de contenido, la discusión de resultados se presenta según los siguientes criterios de análisis: i. frecuencias de palabras en títulos, ii. organización de trabajos según tipo de opción exótica, iii. desagregación de trabajos por abordaje metodológico; iv. temas por períodos de publicación, v. temáticas de trabajos con mayor relevancia según cantidad de citas, y vi. descripción de distribuciones estocásticas del activo subyacente y métodos para la valoración de los contratos.
La Figura 6 5 ilustra el análisis de frecuencia sobre los títulos de las 96 publicaciones relevadas. Entre las palabras más frecuentes se destacan: pricing (39); approach (8); hedging (8); market (8); methods (8); risk (8); Monte Carlo (7); models (7). La elevada frecuencia del término pricing permite inferir que gran parte de los artículos abordan cuestiones de fijación de precios de opciones exóticas. Por su parte, las restantes palabras más frecuentes brindan mayores detalles del trabajo tales como: técnicas empleadas en la valoración (enfoque numérico, método, modelo, simulación Monte Carlo, estático), modelización de la incertidumbre (proceso estocástico, volatilidad, riesgo, proceso de Levy, cambio de régimen, Markov), tipo de opción (barrera, americana, europea) o contribución y resultados (nuevo, eficiente, aplicaciones).
En el Anexo A2 se clasifican las 96 publicaciones obtenidas de la revisión siguiendo dos criterios: tipo de opciones exóticas analizadas, y abordaje metodológico. Para la clasificación por tipología de instrumentos exóticos se emplea el agrupamiento descripto en la sección I. Por su parte, en la desagregación por enfoque metodológico se consideran teóricos a los artículos que presentan definiciones, teoremas o revisiones conceptuales sobre opciones exóticas; teóricos-empíricos a los trabajos que -además de lo anterior- desarrollan aplicaciones numéricas con datos reales o simulados para validar las formulaciones conceptuales planteadas; y empíricos a los documentos que únicamente contienen aplicaciones prácticas.
Dentro de la tipología exótica, el ranking de las opciones con mayor presencia se conforma como muestra la Figura 7, donde las familias de opciones se visualizan agrupadas por colores. Acentuadamente, las opciones barrera son las que se abordan de manera más frecuente dentro de la literatura académica. Las familias de opciones exóticas con mayor presencia son las dependientes de la trayectoria del subyacente (barrera, lookback y asiáticas) seguidas por las dependientes del tiempo (compuestas, chooser y bermudas); las digitales o binarias (puras, activo o nada y dinero o nada); y, en último lugar, las de correlación (arcoíris, basket, entre otras). No se releva ninguna publicación que estudie las opciones boom y crash en particular.

Fuente: elaboración propia.
Figura 7 Gradiente de presencia de diferentes tipos de opciones exóticas
Continuando el análisis por categorías exóticas, se identifican en las publicaciones derivados no tipificados anteriormente, incluidos en el grupo “otros” como: cliquet y reverse cliquet, con cuatro apariciones entre los trabajos analizados (Detlefsen & Härdle, 2007; Guillaume & Schoutens, 2015; Schoutens & Symens, 2003; Veiga et al., 2012), start forward options en dos artículos (Agliardi, 2012; Dziawgo, 2017), y variance swap en tres publicaciones (Abe & Giles, 2008; Abe, 2011; Kirkby & Deng, 2019). Con menor frecuencia aparecen las opciones pasaporte, en forma de escalera, rusa, collar, gap, swing, opciones de montaña, automatic callable, quantile, dual expiry, australian, onion, bi- direction, cap, deductible, power, entre otras. Si se pretende tipificar estas opciones exóticas, puede considerarse que las cliquet y las diferidas o start forward pertenecen a la familia de opciones dependientes del tiempo, mientras que las opciones en forma de escalera, collar, cap, quantile y rusa pertenecen al subgrupo de dependientes de la evolución de S. Finalmente, las opciones de montaña son de tipo correlacionadas.
Si bien no corresponden a tipos de opciones exóticas, también se reconocen en los trabajos recuperados estrategias complejas o combinatorias como strip (Abe, 2011) y diferencial mariposa o butterfly spread (Kadalbajoo et al., 2013; Khaliq et al., 2007; Pindza et al., 2013).
En cuanto a la cantidad de opciones analizadas por trabajo, el 74 % de las publicaciones aborda el estudio de más de un tipo de opción, mientras que solo 25 trabajos analizan un único contrato exótico. En particular, dos de los textos recuperados (Chen, 2009; Zhang, 1995) presentan un análisis teórico de varias familias de opciones. Por otra parte, entre las publicaciones que estudian más de un tipo de opción exótica, las combinaciones más frecuentes son barrera y asiática, y barrera y lookback.
Respecto al momento de ejercicio de las opciones exóticas, las publicaciones se enfocan tanto en opciones europeas como americanas, sin prevalencia alguna. Considerando la naturaleza del activo subyacente, se identifican publicaciones que estudian la valoración de opciones exóticas sobre activos no financieros, como contratos de suministro (Kamat & Oren, 2002; Zhang, Wang et al., 2005); situaciones de riesgo climático (Cortina & Sánchez, 2013); agricultura (Tirupattur et al., 1997); proyectos ecológicos (Dziawgo, 2017); derechos de uso de la tierra (Lu, 2010). También se resaltan los trabajos de Chen et al. (2011) por estudiar mercados emergentes y de García & Sánchez (2015) por analizar las coberturas contra pérdidas en la industria automotriz de Argentina.
Considerando el abordaje metodológico (Anexo A2), más de dos tercios de las publicaciones analizadas se clasifican como teórico-empíricas (67,71 %). Más de la mitad de los trabajos de abordaje teórico y teórico-empírico presentan un desarrollo de modelos mediante formulaciones matemáticas avanzadas para analizar la valoración de los instrumentos exóticos, lo cual es consistente con las revistas de origen. En particular, en los artículos de abordaje teórico-empírico predomina la exposición de modelos formales que luego son meramente ilustrados mediante cálculos o aplicaciones, sin ser el fin último del artículo su aplicación empírica. Solo un trabajo es totalmente empírico (Topper, 2000) donde se demuestra la utilidad del método de elementos finitos para la resolución de modelos financieros formulados como ecuaciones parciales diferenciales con su aplicación a varias opciones exóticas.
Para conocer la evolución temática, se analizan las publicaciones más antiguas y las más recientes. Los trabajos con mayor antigüedad (1995-2005) abordan temas como descripción de los tipos de opciones exóticas, desarrollo de modelos de valoración y estrategias de cobertura, y aplicaciones empíricas sobre subyacentes como el maíz y contratos de electricidad interrumpible. Los métodos Monte Carlo y Black-Scholes también son implementados y comparados en gran parte de tales trabajos. Las opciones más empleadas son las barrera, lookback y asiáticas. Dentro de las publicaciones recientes (2015- 2019), la mitad de ellas se concentra en los primeros dos años y sus temáticas son variadas: distintos métodos de valoración de opciones exóticas, valoración de proyectos de inversión pro-ecológicos, evaluación y cobertura de riesgos del sector automotriz y de activos financieros. Respecto a los métodos, se proponen modificaciones y comparaciones con el modelo de Black-Scholes y se observan diversas aplicaciones del método de simulación Monte Carlo. Las opciones más analizadas son las barrera y lookback.
Considerando la relevancia de las publicaciones, dentro de los trabajos más citados en términos absolutos -citas totales-, Carr et al. (1998) desarrollan, con un enfoque teórico, coberturas estáticas para valorar opciones exóticas dependientes de la trayectoria de activo subyacente (barrera y lookback). Boyle & Draviam (2007) estudian el precio de las opciones cuando la volatilidad del subyacente depende de un proceso de Markov que toma valores discretos, encontrando que la diferencia en los precios de las opciones con y sin cambio de régimen en la volatilidad es sustancial para las opciones lookback y más moderada para las opciones europeas y asiáticas. Kamat & Oren (2002) presentan el diseño y la valoración de contratos financieros para el suministro y la adquisición de servicios de electricidad interrumpibles, proponiendo una nueva modalidad que agrupa contratos de futuros simples con opciones de compra exóticas, con dos precios de ejercicio diferentes.
Por su parte, las siguientes nueve publicaciones más citadas -en términos absolutos- se corresponden mayoritariamente a trabajos de valoración de opciones exóticas con diferentes procesos estocásticos definidos para el precio del subyacente (Beaglehole et al., 1997; Guo & Shepp, 2001; Lin, 1998), mostrando variaciones entre mercados con cantidad de activos finita e infinita (Chen et al., 2008), proponiendo valoraciones a partir de movimientos brownianos geométricos (Lasserre et al., 2006), de esquemas de Pade y descomposición de fracciones parciales (Khaliq et al., 2007), y mediante la herramienta transformación de Esscher para determinar una medida de martingala equivalente (Ching et al., 2007). También incluye trabajos teóricos como el de Schoutens (2006), que describe los métodos de valoración de las opciones exóticas, en el marco de los modelos exponenciales de Levy y otros referidos al riesgo de calibración (Detlefsen & Härdle, 2007). Asimismo, al examinar los trabajos más citados en términos relativos -cantidad de citas por año- se encuentra que también abordan cuestiones de fijación de precios de opciones, proponiendo métodos mejorados, sencillos de implementar, con reducciones en el tiempo computacional, y presentan comparaciones con los mecanismos de valoración tradicional.
Analizando los supuestos sobre las distribuciones estocásticas y los métodos para la valoración de los contratos, la Tabla 7 exhibe los conceptos con mayor presencia en la literatura revisada. En general, la fórmula de Black-Scholes-Merton6 y el método Monte Carlo7 son las herramientas utilizadas con más frecuencia en los estudios considerados.
Tabla 7 Distribuciones estocásticas y métodos de valoración
| Características de distribuciones estocásticas | Métodos y herramientas para valoración |
|---|---|
| Procesos de difusión con saltos | |
| Gaussiana normal inversa (NIG) | |
| Proceso de varianza gamma (VG) | Modelo de Black-Scholes-Merton |
| Movimiento Browniano | (con argumentos de martingala) |
| Movimiento de Laplace | Ecuaciones diferenciales parciales (PDE) |
| Proceso de Levy con cambios temporales aleatorios | Modelos numéricos |
| Varianza conregime switching | Monte Carlo y cuasi Monte Carlo |
| Volatilidad con forma de sonrisa | Otros |
| Modelos de serie de tiempo GARCH | |
| Otros |
Fuente: elaboración propia.
Conclusiones
El presente artículo expone un análisis conceptual sobre opciones exóticas, cubriendo los dos objetivos específicos planteados: presentar los conceptos descriptivos referidos a instrumentos exóticos y realizar una revisión sistemática de la literatura en las principales bases de datos internacionales para conocer la importancia y enfoque brindado a tales instrumentos exóticos en la academia.
Aunque existen abundantes estudios sobre opciones exóticas, resultan escasos los textos académicos que hacen una conceptualización abarcativa del vasto número de instrumentos exóticos existentes en su conjunto, los describen en forma textual -sin adentrarse en cuestiones matemáticas o analíticas complejas referidas a su valoración- y los organizan con distintos criterios de clasificación (Buchen 2012; Mascareñas, 2013; Zhang, 1995). En ese sentido, la conceptualización, descripción y clasificación de 25 tipos de opciones exóticas efectuadas en respuesta al primer objetivo específico, procuran contribuir a incrementar la escasez de los mencionados estudios. De este modo, la sección I brinda a los lectores un marco conceptual para la inmersión en el tema y puede constituirse como material educativo para cursos de finanzas de instituciones de educación superior. En añadidura, los hallazgos de la sección III, literal B -donde se identifican 30 trabajos teóricos sobre el tema- resultan un complemento para quienes deseen profundizar su estudio desde una perspectiva conceptual.
Por otra parte, tampoco se han identificado investigaciones que reporten cuál es el estado del arte sobre opciones exóticas, indaguen la evolución de la temática, reconozcan áreas poco estudiadas y detecten inconsistencias entre teoría y práctica o hallazgos empíricos contradictorios. Por lo tanto, la revisión sistemática de la literatura aquí realizada por el presente estudio en bases de datos de nivel internacional se considera de relevancia y de interés para la comunidad científica. En particular, los resultados provenientes del proceso de revisión bajo protocolo expuestos en la sección III, junto con el examen conceptual del apartado I, permiten extraer implicancias desde diferentes dimensiones de análisis.
Con base en las 96 publicaciones encontradas, los hallazgos de la revisión sistemática muestran que las opciones exóticas representan un tema vigente, en auge durante la última década: temporalmente, la mayoría de los estudios recuperados (63,54 %) se ubica entre 2006 y 2015, siendo 2013 el año con mayor cantidad de trabajos en el tema. Asimismo, se identifican las 12 publicaciones de mayor impacto: tres ellas con más de 47 citas (Carr et al., 1998; Boyle & Draviam, 2007; Kamat & Oren, 2002) y las nueve restantes con un número de citas entre 16 y 30. Estas publicaciones representan un conjunto de estudios recomendables de analizar para todo investigador que aborde el tema.
Considerando el objetivo de las publicaciones examinadas, la mayoría se refiere a la fijación de precios de opciones exóticas o sus problemas de valoración, siendo escasos aquellos trabajos que efectúan una aplicación de tales instrumentos para resolver problemáticas reales (Cortina & Sánchez, 2013; Dziawgo, 2017; García & Sánchez, 2015; Kamat & Oren, 2002; Lu, 2010; Tirupattur et al., 1997; Zhang, Wang et al., 2005). De esta forma, se observa que predomina la búsqueda de precisión y mejoras en cuestiones de valoración (mejor calibración del riesgo, reducción del tiempo computacional de procesamiento), por sobre la explotación de la ventaja de este tipo de instrumentos: su flexibilidad y versatilidad para adaptarse a innumerables problemas de la vida real. La preponderancia de la valoración por sobre la flexibilidad, también se deriva de la estructura de los trabajos con abordaje teórico-empírico cuyo contenido mayoritario corresponde a desarrollos matemáticos y, en una breve sección empírica, se efectúa una aplicación numérica -en general con datos simulados- simplemente para validar la formulación teórica. En ese orden de ideas, a partir de la revisión sistemática de literatura, se detecta una brecha de interés para la investigación, al hacer explícita la escasez de estudios que exploten la flexibilidad de los instrumentos exóticos y los apliquen a problemas de valoración y coberturas sobre situaciones reales, complejas y controvertidas, con subyacentes no financieros.
Además, en línea con la escasez de estudios empíricos stricto sensu (aplicación para resolver problemática con datos reales), de la revisión sistemática efectuada no se obtienen trabajos empíricos generales de opciones exóticas negociadas en los mercados financieros, más vinculados a la perspectiva del inversor, un tema que ya ha sido advertido años atrás por Crespo (2001) para el contexto español.
Respecto a las opciones exóticas utilizadas en los trabajos analizados, se destacan con preeminencia las dependientes de la trayectoria del precio del subyacente, en especial, las opciones barrera, lookback y asiáticas, en ese orden. Así, se identifica otra brecha en el campo del conocimiento que invita al desarrollo de investigaciones sobre los instrumentos exóticos menos examinados: opciones boom y crash, de correlación o categorizadas como “otros”. Asimismo, es dable destacar en este punto, que el Anexo A2 representa un aporte sustancial para investigadores interesados en alguna tipología particular de opciones exóticas porque identifica los trabajos específicos sobre la temática, segregados por tipo de abordaje.
Como complemento de la investigación documental de autores clásicos, los hallazgos del presente artículo provienen de un proceso de relevamiento sistemático donde los términos de búsqueda se rastrean solo en el campo título de los metadatos y no se incluyen términos referidos a tipos específicos de opciones. Si bien esto otorga especificidad al trabajo, también puede considerarse una limitación que podría sortearse en futuros estudios con búsquedas en campos diferentes de los metadatos (resumen, palabras clave) o incluyendo vocablos referidos a ciertas opciones exóticas de interés para el investigador.
Como implicancias prácticas del artículo, es esperable que la difusión y el aporte para esclarecer la comprensión del tema deriven en una mayor utilización de los instrumentos exóticos en los mercados, a fin de aprovechar sus menores primas en algunos casos y las condiciones más ajustadas a situaciones reales provocando coberturas eficientes, así como adoptar su uso para otro tipo de activos o situaciones espinosas y controversiales, donde se requiere flexibilidad sobre ciertas reglas del contrato.