INTRODUCCIÓN
La relación entre crecimiento económico y distribución del ingreso se ha discutido ampliamente en la literatura económica y entre los hacedores de política. Tal vez uno de los trabajos más influyentes en la literatura es el de Kuznets (1955). La hipótesis de Kuznets (1955) plantea que la desigualdad económica deberá incrementarse a corto plazo ante una economía en crecimiento para alcanzar un menor nivel de desigualdad a largo plazo. Es decir, la desigualdad de ingresos deberá sacrificarse a corto plazo para alcanzar el crecimiento que llevará a la reducción de la desigualdad a largo plazo.
Desde el trabajo seminal de Kuznets, muchos autores han tratado de comprobar su hipótesis. Los primeros trabajos se dedicaron a hacer modificaciones a las variables propuestas por él. Modificaban los supuestos iniciales sobre las causas de los cambios en la desigualdad, proponían adicionar dimensiones como la población y la política económica como factores influyentes en la desigualdad a corto y largo plazo para economías en crecimiento.
Debido a la falta de datos de series de tiempo, la mayoría de los trabajos empíricos se dedicó a analizar la desigualdad en un período determinado para varios países, empleando datos de corte transversal. El contraste se daba entre los países desarrollados y los países emergentes. Se suponía que la economía de los países emergentes representaba los efectos a corto plazo, mientras que el estado de la economía en los países desarrollados mostraba el cambio a largo plazo. Cada estudio se diferenciaba de sus predecesores por los países incluidos en su análisis y las variables seleccionadas como relevantes para la medición de los efectos en la desigualdad.
Por ejemplo, Bourguignon y Morrison (1998) incluyeron productividad laboral por sectores económicos; Williamson (1997) agregó variables demográficas, como la distribución de la edad. Otros autores incluyeron dentro del modelo de Kuznets variables como corrupción (Gupta, Davoodi & Alonso-Terme, 1998), distribución inicial de los activos (Deininger & Squire, 1998) y tasa de cambio (Bahmani-Oskooe, Goswami & Mebratu, 2006) entre otros. Ángel (2010) reemplaza la variable principal de la hipótesis de Kuznets (el producto interno bruto (PIB) per cápita) por el empleo como indicador del desarrollo económico.
Otras aproximaciones han buscado variar la especificación del modelo; por ejemplo, Lin, Suen, Yeh y Huang (2007) comprobaron la hipótesis empleando inferencia bayesiana y regresiones semipa-ramétricas para datos de corte transversal siguiendo a Huang, Lin y Weng (2006). Algunos autores prueban la hipótesis para países emergentes, por ejemplo Ikemoto y Uehara (2000) en Tailandia, añadiendo variables como la inversión extranjera.
Siguiendo esta línea de investigación, el objetivo de este estudio se centra en evaluar la hipótesis de Kuznets para Colombia durante el período 1977-2005. Para lograr nuestro objetivo seguiremos la propuesta de Bahmani-Oskooee y Gelan (2008). Esta aproximación emplea el PIB per cápita, la población y la tasa de cambio nominal como factores que afectan la desigualdad económica. A diferencia de trabajos anteriores emplearemos, por un lado, datos de series de tiempo aplicando un modelo de corrección de errores para observar los efectos a corto plazo, y por otro lado, pruebas de cointegración y modelos de vectores autorregresivos (VAR) para estudiar los efectos a largo plazo.
El presente documento se destaca por tres características que le dan su valor agregado frente a la literatura preexistente. En primer lugar, por la recopilación de información para cuatro series de datos, de importancia macroeconómica, para un largo período de tiempo: 1977-2005, información que pocos países disponen de forma continua. Un segundo aspecto es el análisis empírico de la hipótesis de Kuznets en un país latinoamericano, estudio que no se ha presentado antes. Finalmente, nuestro trabajo resalta, entre otros, por la aproximación utilizada para la comprobación de la hipótesis de Kuznets, pues, en lugar de hacerlo como la literatura lo ha hecho antes, analizando contrastes entre países con diferentes etapas de desarrollo, nuestro estudio, aprovechando el uso de técnicas de series de tiempo, prueba la hipótesis observando para un mismo país, durante un periodo de tiempo, los efectos a corto y largo plazo de las variables macroeconómicas de interés.
Este documento se encuentra organizado de la siguiente manera: la primera parte corresponde a esta introducción. En la siguiente sección se discute la metodología y los datos que se emplean en el ejercicio. La tercera sección aborda algunas características de las series de tiempo empleadas. La cuarta sección presenta los resultados de las estimaciones, y la última sección, los comentarios finales.
METODOLOGÍA, DATOS
Bahmani-Oskooee y Gelan (2008) asumen la siguiente relación a largo plazo entre la desigualdad de ingresos, medida por el coeficiente de Gini (GINI) y el PIB real per cápita (PIB), la población (POB) y la tasa de cambio nominal (TASA). Formalmente, esto implica la existencia de un vector de constantes *P1x4 que generan una combinación lineal del vector de variables aleatorias integradas de orden uno, yt = [GINIt PIBt POBt TASA t ]T ~I(1), que será estacionario o integrado de orden cero (|(0)). Es decir,
El vector de constantes Ψ1x4 se puede normalizar de la siguiente manera:
La hipótesis de Kuznets a largo plazo implica que a1 sería negativo. Es decir, si es cierto que el crecimiento económico reduce la desigualdad, se esperaría que a1 fuera negativo. Por otro lado, la literatura empírica sugiere que el aumento en la población empeora la desigualdad; por lo tanto α2 debería ser positivo. Finalmente, si la depreciación de la moneda incrementa la desigualdad, el coeficiente asociado a ella, α3 debería ser positivo.
La ecuación [1] refleja el comportamiento de las variables a largo plazo, mientras que el comportamiento a corto plazo estará dado por el modelo de corrección de errores. Es decir,
donde zt corresponde a los desequilibrios respecto a la relación a largo plazo en el periodo t. En otras palabras, zt = Ψyt . El vector y corresponde al vector de coeficientes de ajuste a desequilibrios a largo plazo. En especial, el primer elemento de y muestra cómo es el ajuste a corto plazo de la distribución del ingreso frente a desequilibrios.
Por otro lado, dada la relación a largo plazo, el sistema conformado por las variables en el vector y t también se puede expresar por medio de un modelo VAR (vector autorregresivo) como el siguiente:
El VAR permite encontrar la respuesta de cada variable a choques inesperados de las demás variables. Esto es, posibilita encontrar las funciones de impulso respuesta.
Para estimar los modelos descritos anteriormente emplearemos datos trimestrales desde el primer trimestre de 1977 hasta el cuarto trimestre de 2005 para las siguientes variables: coeficiente de Gini para las trece ciudades principales de Colombia (medido como una proporción de 1 a 100), producto interno bruto per cápita (medido en millones de pesos constantes por habitante), tasa de cambio nominal (medida en pesos por dólar) y población total (medida en número de personas). La población y el coeficiente de Gini proceden de las estadísticas históricas del Departamento Nacional de Planeación. La serie del PIB sin desestacionalizar y a precios constantes fue extraída del Departamento Nacional de Estadística. La tasa de cambio nominal se obtuvo del Fondo Monetario Internacional.
El período de estudio se escoge siguiendo dos criterios. Primero se busca cubrir el rango de tiempo más extenso posible para tener una perspectiva a largo plazo en el estudio. Después se desea emplear la frecuencia más alta posible de los datos para permitir evaluar el comportamiento a corto plazo de la relación entre crecimiento y desigualdad del ingreso. Siguiendo estos dos criterios se eligió trabajar con datos trimestrales para el periodo 1977-2005.
Las series de datos por analizar son las más actualizadas que pudieron conseguirse en las bases de datos oficiales, tanto nacionales como internacionales, con periodicidad trimestral. No fue posible hacer el estudio sobre las series más allá de 2005 debido a los cambios en las metodologías de cómputo de las series. La serie del coeficiente de Gini tuvo un cambio para los años de 2006 y 2007. La Misión para el Empalme de las Series de Empleo, Pobreza y Desigualdad logró empalmar las dos metodologías solo para los años de 2002 a 2010, sin embargo, los datos de los años de 2006 y 2007 se perdieron quedando una brecha que impide darle continuidad a la serie y trabajar con ella para este tipo de análisis.
Características de las series
Para establecer el orden de integración se emplearon las pruebas de raíces unitarias de Dicky-Fuller aumentada (ADF), la prueba de Phillips-Perron (PP), la prueba de Kwiatkowski, Phillips, Smichdt y Shin (KPSS), la prueba Breitung y la prueba Hegy para series estacionales, los resultados de las pruebas se presentan en la Tabla 1. En las pruebas que no tienen en cuenta la estacionalidad, como la KPSS, PP y la Breitung para todas las variables, al menos dos de ellas concluyeron que las series eran integradas de orden uno I(1).
Para las pruebas ADF y HEGY, que tienen en cuenta la inclusión de variables dicotómicas de estacionalidad, la conclusión fue consistente con las pruebas anteriores. En todos los casos se encontró que las series no presentaban raíces unitarias en sus diferencias. Con la prueba de HEGY (Tabla 2) se observa que las series no presentan raíces estacionarias no estacionales, tampoco se encuentran raíces anuales o bianuales en sus niveles ni en sus diferencias. En general, todas las pruebas permitieron concluir que las series eran integradas de orden uno I(1).
RESULTADOS
Con las pruebas de cointegración se pudo comprobar la existencia de una relación a largo plazo entre las variables analizadas, esto es, entre el coeficiente de Gini, la población, el PIB per cápita y la tasa de cambio (representada en la ecuación [1]). Dada esta relación, fue posible estimar el modelo de corrección de errores (ecuaciones [2] y [3]) para establecer el comportamiento de las variables a corto plazo ante choques exógenos inesperados y observar la velocidad con la que se ajustan para restablecer el equilibrio a largo plazo.
Verificar la existencia de la relación a largo plazo entre las variables requiere, en primer lugar, comprobar si las series son integradas de orden uno, es decir, determinar si yt~I(1) lo cual se constató con las pruebas de raíces unitarias, y en segundo lugar verificar la cointegración de las mismas.
Para comprobar la existencia del vector de cointegración (Ψ1x4) del modelo teórico se usaron las pruebas de Johansen y de Phillips y Oullaris(1). En la Tabla 1 se presentan los resultados para las dos versiones de la prueba de Johansen: valor propio máximo (λMAX) y traza (λTraza). Los resultados de estas dos pruebas permiten concluir que existe una relación a largo plazo entre las variables consideradas. De la misma forma, los resultados de la prueba de Phillips y Oullaris (ver Tabla 2) confirman dicha relación.
Tabla 3 Prueba Johansen de cointegración
| λMAX | λTraza | ||||||||
| Estadístico | 10% | 5% | 1% | Estadístico | 10% | 5% | 1% | ||
| r < = 3 | 507 | 7.5 | 9.2 | 13.0 | 5.7 | 7.5 | 9.2 | 13.0 | |
| r < = 2 | 9.2 | 13.8 | 15.7 | 20.2 | 15.0 | 17.9 | 20.0 | 24.6 | |
| r < = 1 | 12.5 | 19.8 | 22.0 | 26.8 | 27.4 | 32.0 | 34.9 | 41.1 | |
| r = 0 | 26.3 | 25.6 | 28.1 | 33.2 | 53.8 | 49.7 | 53.1 | 60.2 | |
Comprobada la condición de cointegración de las series (expresada en el vector de cointegración, Ψ, de la ecuación [1]) se estima el modelo de corrección de errores y el modelo VAR expuestos en las ecuaciones [2] y [3] respectivamente.
En la Tabla 3 se muestra la estimación del vector de cointegración (Ψ), obteniendo los signos esperados para los comportamientos de las diferentes variables. En especial resalta la relación negativa entre el PIB per cápita y el coeficiente de Gini, resultado que confirma la hipótesis de Kuznets.
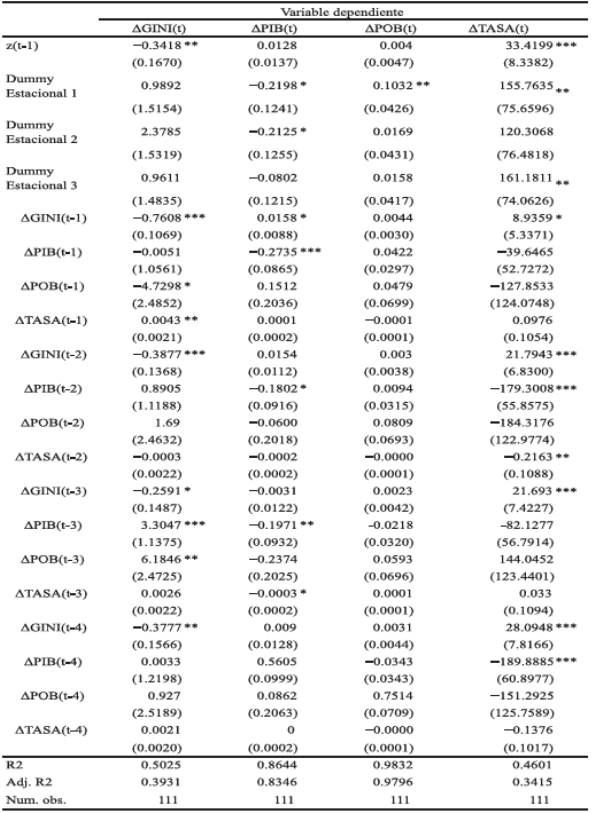
En la Tabla 4 se indica la estimación del modelo de corrección de errores(2). Los resultados muestran que ni el PIB per cápita ni la población se ajusta a desequilibrios a corto plazo. Las variables que se ajustan ante desequilibrios a corto plazo son el coeficiente de Gini y la tasa de cambio. Se observa que un desequilibrio positivo implicará una disminución a corto plazo del coeficiente de Gini en 0.3418 puntos porcentuales. Es decir, tanto los efectos a corto y largo plazo corresponden a la dirección esperada en la hipótesis de Kuznets. El PIB per cápita tiene un efecto positivo sobre la distribución del ingreso a largo plazo (una caída en el coeficiente de Gini). Por otro lado, un desequilibrio negativo a corto plazo (asociado con un crecimiento del PIB por encima del equilibrio a largo plazo) implicaría a corto plazo un incremento en la desigualdad.
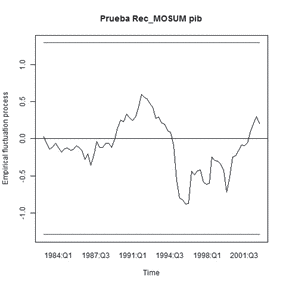
En la Tabla 5 se presenta la estimación del modelo VAR con 5 rezagos. Este modelo no muestra autocorrelación ni heterocedasticidad(3). Con este se pretende evaluar las funciones impulso-respuesta para cada una de las series, una vez verificada la estabilidad de algunas de ellas. Dado que el periodo de estudio es relativamente grande, se podría esperar que cambios estructurales en la economía colombiana generaran un cambio en los coeficientes. Los resultados de estas pruebas se exponen en el Anexo 2. En todos los casos se puede concluir que no existe cambio estructural durante el periodo de estudio y por tanto se puede proceder al análisis de las estimaciones derivadas del modelo VAR.
En la Figura 1 se expresa el efecto de un cambio inesperado en el PIB per cápita sobre el coeficiente de Gini. En este caso, solo se observa un aumento en el coeficiente de Gini cuatro trimestres después del choque positivo inesperado. Es decir, solo cuatro periodos después, la distribución del ingreso empeora tras un aumento del PIB per cápita. Para los otros períodos el efecto desaparece.
En la Figura 2 y la Figura 3 se presenta la respuesta del coeficiente de Gini ante cambios inesperados en la población y la tasa de cambio, respectivamente. El coeficiente de Gini disminuye ante el cambio en la población después de cinco períodos y nuevamente se vuelven a ver sus efectos cinco períodos más tarde (en el décimo trimestre).
El efecto del cambio inesperado de la tasa de cambio sobre el coeficiente de Gini se observa después de siete períodos y perdura durante un trimestre completo. Después del octavo período, el coeficiente de Gini no responde a cambios inesperados de esta variable.

Figura 1 Función impulso respuesta del coeficiente de Gini ante cambio inesperado en el PIB per cápita.
COMENTARIOS FINALES
La hipótesis de Kuznets (1955) implica que un aumento en el PIB per cápita incrementa la desigualdad del ingreso a corto plazo, pero a largo plazo dicho crecimiento debería generar una mejora en la distribución del ingreso. Nuestro estudio explota la base de datos histórica disponible en el Departamento de Planeación Nacional. Típicamente, el contraste de la hipótesis de Kuznets implica emplear bases de datos de corte transversal. En este sentido, este documento es un aporte, pues emplea series de tiempo para constatar esta hipótesis para el caso colombiano.
Por otro lado, se encontró que en efecto la desigualdad de ingresos se ve empeorada a corto plazo ante crecimientos de la economía. En oposición a lo que ocurre a largo plazo, en que el desarrollo económico disminuye la desigualdad. Nuestros resultados sugieren que la hipótesis de Kuznets puede explicar la relación entre crecimiento económico y distribución del ingreso en Colombia durante el periodo 1977-2005. Adicionalmente, no se encuentra efecto a corto plazo sobre la distribución del ingreso generado por el crecimiento poblacional ni por la tasa de cambio. A largo plazo se halla que el aumento en la población empeora la desigualdad y que la depreciación del peso incrementa la desigualdad.
Los resultados permiten extrapolar las conclusiones al periodo 2006 a 2015, en el que la distribución del ingreso mejoró, al mismo tiempo que el PIB presentó un crecimiento relativamente alto y una tasa de cambio apreciada. No obstante, serán necesarias futuras investigaciones con bases de datos más actualizadas para constatar estos resultados.