INTRODUCCIÓN
Ampliamente definido a nivel mundial, el tipo de cambio es el precio de una moneda en términos de otra. Expresa la cantidad de moneda doméstica que hay que pagar para adquirir una moneda extranjera (divisa), según el Banco Central de Venezuela (BCV, 2016), permitiendo el desarrollo de relaciones comerciales entre individuos, empresas o países. Es importante distinguir entre el tipo de cambio nominal (TCN), que para Samuelson y Nordhaus (2010) es el monto de moneda extranjera que se puede comprar con una unidad de moneda doméstica, y el tipo de cambio real (TCR) que, según Bernanke y Frank (2007), indica el precio medio de un bien o servicio en el interior del país, expresado en el precio medio de dicho bien o servicio en el mercado extranjero, lo que hace referencia a un precio relativo1.
En todas las economías abiertas del mundo, esta es una de las variables ma croeconómicas más importantes y, desde el punto de vista econométrico, es una de las series de tiempo más interesantes. El sistema mediante el cual se determina el tipo de cambio que rige en la economía de un país puede ser de dos tipos: i) sistema de tipo de cambio flexible y 11) sistema de tipo de cambio fijo.
En el sistema de tipo de cambio flexible, se fija la paridad mediante las fuerzas de la oferta y la demanda de divisas en el mercado, donde participan todos los agentes económicos2. Los países que cuentan con un sistema cambiario de tipo flexible tienen como consecuencias sobre sus economías: políticas monetarias independientes, necesidad de menos activos de reserva por parte de la autoridad monetaria, alta disciplina fiscal por parte del gobierno, además de ser un estabilizador automático de los choques de demanda; sin embargo, los tipos de cambio flexibles son más volátiles, esto afecta al comercio, demanda el desarrollo de mecanismos de cobertura y retrasa los ajustes en la asignación de recursos, lo que aumenta la variabilidad de la moneda local frente a la divisa de referencia.
En el sistema de tipo de cambio fijo, el Estado toma total control del mercado de divisas, dejando de lado las fuerzas de la oferta y la demanda; crea un mecanismo que permite vigilar el mercado, instau rando lo que se conoce como un control de cambio. Este no es más que la inter vención oficial del mercado de divisas a través del diseño de un régimen adminis trativo, que siempre está acompañado por un conjunto de restricciones cuantitativas y cualitativas sobre la compra y venta de moneda extranjera. La fijación del tipo de cambio también es un instrumento de política cambiaria, con el fin único de controlar las entradas o salidas de capital, y su efectividad depende de las causas que han llevado a su implementación, de los objetivos planteados por los hacedo res de política económica y la forma en que se implementa y opera en la práctica (Dornbusch, Fischer & Startz, 2009). Las consecuencias del control de cambio son básicamente: un estímulo para la disci plina monetaria3, reducir la especulación sobre la moneda nacional, proteger las reservas internacionales, la balanza de pago y el tipo de cambio nominal, la implementación de controles de precios sobre bienes, con la finalidad de prevenir la formación de un proceso inflaciona rio y regular automáticamente choques monetarios, permitiendo a los agentes económicos equilibrar sus tenencias de divisas porque transan moneda extranjera con la principal autoridad monetaria, esto busca que la volatilidad de la moneda local sea menor.
La era de la libre convertibilidad de las monedas permitió dejar atrás una serie de problemas asociados al control de la paridad cambiaria; el más conocido, la creación de un mercado paralelo de divisas. En este mercado se realizan operaciones de compra y venta de monedas extranjeras, la cotización en moneda nacional es fijada por el libre juego de la oferta y la demanda, pero al margen de la ley. A pesar de que el sistema cambiario fijo tiene como norte reducir la volatilidad de la moneda local respecto a la extranjera, el mercado paralelo que, por naturaleza, se crea, causa el efecto contrario, porque eleva la volatilidad del tipo de cambio nominal paralelo, distorsionando todo el entorno económico.
La economía venezolana ha estado sometida a las rigurosidades de un excesivo control cambiario desde el año 2003, que maneja el mercado de divisas, tanto en términos de cantidad como de precio. Instaurado con la finalidad de evitar la fuga de capitales y la disminución de las reservas internacionales del país, las consecuencias que ha tenido la medida sobre el sistema económico han sido múltiples. La más conocida, el surgimiento de un mercado paralelo al mercado oficial, que deforma todo el aparato productivo de la economía, repercutiendo en la calidad de vida de los venezolanos. Esto ha hecho que una de las variables económicas de referencia para fijar precios de algunos bienes y servicios sea el tipo de cambio paralelo, porque el mercado no oficial cubre parte de la demanda de divisas. Durante el periodo que se estudia, la variación que ha sufrido el precio de la moneda extranjera en términos de la moneda nacional supera el 30500 %. Esta gran variabilidad despierta el interés de propios y extraños. Y es, precisamente, la característica en donde se enfoca este trabajo: la volatilidad del tipo de cambio paralelo.
El estudio de la volatilidad de las series de tiempo es un tema que durante años ha atraído el interés de muchos investigadores en esa área. Los últimos 35 años han marcado un antes y un después en la forma de abordar todo lo referente a este campo. Los desarrollos de Engle (1982), Bollerslev (1986) y Taylor (1986) fueron el punto de partida para estructurar un gigantesco y creciente marco teórico de referencia: la familia de los modelos autorregresivos de heterocedasticidad condicional (ARCH). Estos modelos se enfocan en analizar el comportamiento de la varianza condicional de la variable de interés, empleando métodos de estimación ampliamente conocidos; es allí donde radica su riqueza. Además, las series temporales de alta frecuencia que se observan en los mercados financieros y cambiarios vienen caracterizadas por ser asimétricas, leptocúrticas y con una elevada persistencia en volatilidad (Sánchez & Reyes, 2006).
Es justamente la combinación de estos dos elementos: i) la volatilidad del tipo de cambio paralelo y 11) los modelos estocásticos de volatilidad disponibles para su análisis, lo que marca la hoja de ruta de la presente investigación. Con el objetivo de evaluar la conjunción de estos dos aspectos, se lleva a cabo la estimación de modelos estocásticos de volatilidad para 2869 observaciones de la variable de interés, y resalta, particularmente, la asimetría de las perturbaciones sobre la volatilidad del tipo de cambio paralelo y su persistencia sobre los valores futuros. Teniendo en mente la gama de modelos estadísticos existentes para estudiar las series de tiempo, desde el contexto uniecuacional, y la disponibilidad de herramientas computacionales, este estudio busca revelar el comportamiento de la variable tipo de cambio paralelo de Venezuela (TCP), mediante el uso de modelos estocásticos que tienen como principal componente la volatilidad de la serie.
El artículo está organizado en cinco secciones, además de la introducción. La primera hace referencia a la evolución del tipo de cambio paralelo en Venezuela; la segunda muestra el marco teórico sobre los principales modelos estocásticos de volatilidad; la tercera sección describe la metodología utilizada; la cuarta sección ubica los resultados y las discusiones asociadas; y la quinta sección presenta las principales conclusiones encontradas.
EVOLUCIÓN DE LOS TIPOS DE CAMBIO EN VENEZUELA 2003 2015
En los años 2001 y 2002 se registró una caída en las reservas internacionales venezolanas de 19,77 %, producto de la inseguridad política que vivía el país. En febrero del 2002, Venezuela mantuvo sus bandas cambiarias y el dólar se cotizó en 0,793 Bs/USD para la venta, hasta la entrada en vigencia de un esquema de flotación, que llevó el tipo de cambio a 0,981 Bs/USD para la venta, según cifras del BCV. El 5 de febrero de 2003 se instaura un control cambiario en el país y se crea la Comisión de Administración de Divisas (CADIVI). Durante este largo periodo se han establecido distintas instituciones con la finalidad de paliar los efectos del mercado paralelo. En junio de 2010 entró en vigencia el Sistema de Transacciones con Títulos en Moneda Extranjera (SITME), dirigido a importaciones no prioritarias, utilizado de forma muy limitada por la población para ciertas operaciones, y se mantuvo hasta febrero de 2013. En marzo del año 2013 se creó el Sistema Complementario de Administración de Divisas (SICAD), su valor se fijaba por subastas pero los resultados no fueron los esperados. Para enero de 2014 CADIVI pasó a formar parte del Centro Nacional de Comercio Exterior (CENCOEX) y el país mantuvo un sistema de cambio dual. En febrero de 2014 el ente rector decidió modificar la Ley de Régimen Cambiario y sus ilícitos y crear el SICAD 11, que funcionaba igual que el SICAD I, pero permitía el acceso a un mayor número de sectores económicos, incluyendo personas naturales. Para febrero de 2015 las autoridades venezolanas anunciaron el funcionamiento de un sistema cambiario de tres mercados: 1) CENCOEX; 2) SICAD (unificación del SICAD I y 11) y, 3) Sistema Marginal de Divisas (SIMADI), donde el precio de dólar estadounidense fluctúa en función del libre juego de la oferta y la demanda.
En la Tabla 1 se puede apreciar la evolución de la moneda nacional después del establecimiento del control cambiario de 2003 y los sectores a quienes estaba dirigido; mecanismo de control que sigue vigente.
Tabla 1 Evolución del control de cambio en Venezuela, 2003-2015

* Precio del dólar al cierre del mes de noviembre.
El control de cambio vigente en Vene zuela desde el año 2003 ha distorsionado toda la economía del país, por el aumento constante del tamaño del mercado pa ralelo, debido a las limitaciones en la asignación de divisas; reflejo claro es el comportamiento de los principales agre gados macroeconómicos: la disminución de la tasa de crecimiento del producto interno bruto (PIB), el aumento de la tasa de inflación y la disminución de las reservas internacionales, por mencionar algunos, como se constata en la Tabla 2, que confirman la ineficiencia de la medida de política cambiaria. Desde entonces, el restringido mercado oficial coexiste con un mercado paralelo ilegal creciente.
Durante los primeros años existió una cotización paralela del dólar, denominada informalmente como el "dólar CANTV"4, vigente hasta mayo del año 2008, cuando el Gobierno nacionalizó la Compañía Anónima Nacional Teléfonos de Venezuela (CANTV), eliminando toda posible operación cambiaria. Le siguió el "mercado permuta"5, al que se accedía a través de bonos en moneda extranjera emitidos por el BCV, cuyo precio llegó casi a duplicar la tasa oficial vigente para ese momento. En mayo de 2010 el Gobierno suspendió el mercado permuta debido a "irregularidades" en su funcionamiento, a pesar de que este mercado suministraba entre el 15 % y 20 % de las divisas requeridas por el sector privado, pero el diferencial entre el tipo de cambio oficial y el no oficial era cercano al 300 %, administrativamente inviable para las autoridades por las repercusiones sobre los precios.
Después del cierre del mercado permuta, la determinación de la tasa del tipo de cambio paralelo se estableció con el llamado "dólar Cúcuta", que toma en cuenta el tipo de cambio fronterizo en bolívar/peso (TCF) con la ciudad de Cúcuta (Colombia) a través de la oferta y demanda de bolívares en esa ciudad, y la información del BCV referente a la liquidez monetaria (M2) dividida entre las reservas internacionales (RR11) de Venezuela, es decir, el tipo de cambio implícito, para finalmente fijar como precio de referencia del dólar paralelo el promedio de los dos anteriores6.
Las presiones en el mercado paralelo han sido crecientes. La caída del precio del petróleo ha disminuido los ingresos del gobierno en dólares, recortando los cupos de divisas, lo que obliga a muchas personas e instituciones a acudir al mercado paralelo para conseguir los dólares que necesitan. Esto presiona la subida del tipo de cambio paralelo ampliando la brecha con el tipo de cambio oficial, que a su vez, presiona al Gobierno para que, tarde o temprano, devalúe el bolívar. Esta situación se convierte en un espiral negativo para la economía del país. Además, debe añadirse el hecho de que la cotización que se usa como marcadora es de frontera, con todas las limitaciones que ello implica; este tipo de cambio deja de lado las operaciones más refinadas que hace el sector corporativo venezolano; además, la dinámica fronteriza en Venezuela está fuertemente distorsionada por el fenómeno del contrabando; no obstante, el marcador de las operaciones de frontera, con sus imperfecciones, es la única referencia válida que se tiene sobre el tipo de cambio paralelo (Ecoanalítica, 2014).
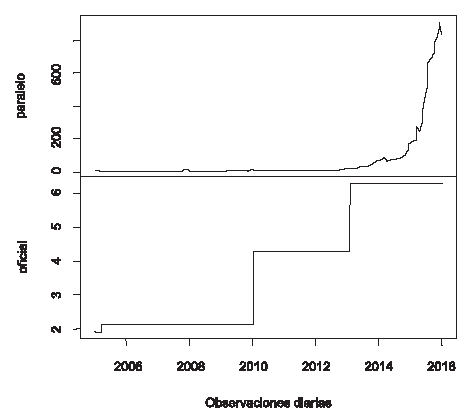
En la Figura1 se puede apreciar la evolución del tipo de cambio del dólar paralelo frente al dólar oficial. La brecha creciente entre ambas cotizaciones estimuló la actividad especulativa y llevó a ajustar varias veces la tasa oficial hacia arriba, con la esperanza de disuadir el diferencial. Pero en la medida que se hacía más difícil adquirir divisas legalmente, mayor era la demanda en el mercado paralelo y, por lo tanto, mayor la diferencia entre el tipo de cambio de este mercado y el tipo de cambio oficial, hecho económico evidente.
Es importante destacar en este punto el crecimiento significativo que ha tenido la liquidez monetaria durante el periodo estudiado, como se observa en la Tabla 2. Esto permite suponer una fuerte relación entre la expansión monetaria y el aumento de la cotización del tipo de cambio paralelo, ambos con comportamiento creciente desbordado. Dicha relación se asume, tomando en consideración el famoso modelo de overshooting7 de Dornbusch (1976); modelo dinámico bajo expectativas racionales que intenta explicar la gran volatilidad de los tipos de cambio como consecuencia de un aumento inesperado en la cantidad de dinero (liquidez monetaria). Concretamente, ante un estímulo monetario el tipo de cambio sobrerreacciona, reflejando la diferencia de velocidades en el ajuste del mercado de activos financieros y el mercado de bienes. El tipo de cambio se ajusta rápidamente en el primer mercado, mientras que en el segundo lo hace lentamente. En consecuencia, toda expansión monetaria aumenta la liquidez, disminuye la tasa de interés y deprecia el tipo de cambio por encima de su nivel de equilibrio a largo plazo8.
MARCO TEÓRICO
Las variables financieras y cambiarias tienen la particularidad de responder a los acontecimientos ocurridos con anterioridad, para determinar, en líneas generales, su comportamiento futuro. La volatilidad puede ser entendida como la relación existente entre el pasado y el presente de una serie de tiempo, medida por la magnitud de esa relación, tomada como una medida de riesgo de los activos financieros.
La volatilidad es una medida de la intensidad de los cambios aleatorios o impredecibles en la rentabilidad o en el precio de un título; en la representación gráfica de una serie histórica de rendimientos se asocia la volatilidad con la amplitud de las fluctuaciones del rendimiento tanto es que se consideren en valor absoluto como en desviaciones alrededor de un valor medio (Márquez, 2002)
No existe una definición concreta y generalizada de volatilidad, lo que sí es aceptado universalmente es que la volatilidad se refiere a un periodo en el cual la serie de tiempo presenta alta variabilidad o una varianza creciente (Baillie, 2006). Las características propias de una serie de tiempo con volatilidad son:
Exceso de curtosis (Mandelbrot, 1963; Fama, 1963).
Persistencia o conglomerado de volatilidad (Mandelbrot, 1963; Engle 1982). Los periodos de alta volatilidad son seguidos de periodos de volatilidad elevada, y los de baja volatilidad operan de forma análoga a corto plazo.
Existencia de discontinuidades en la serie (Figlewski, 1997), es decir, valores elevados de la serie en momentos específicos.
Comportamiento asimétrico de las series temporales, según la noticia que afecte la serie (Campbell, 1987; Hentschel, 1995).
Los períodos de alta o baja volatilidad son seguidos de períodos en los que la volatilidad es moderada a largo plazo (Hsieh, 1995; Figlewski, 1997).
En el estudio de las series de tiempo, la volatilidad se relaciona con la varianza condicional9 de la serie. En general, esta última no es constante y, en consecuencia, los modelos de series de tiempo tradicionales, que suponen varianza homocedástica, no son adecuados para modelar este tipo de series. Es necesario asociar la varianza a una distribución de probabilidad concreta para poder utilizarla como medida del riesgo de activos financieros (Poon & Granger, 2003).
La volatilidad permite estimar y medir el efecto de los cambios que no se pueden predecir; estudios sostienen que la volatilidad puede ser de dos fuentes: i) determinista, que no cambia a lo largo del tiempo y si cambia es de forma conocida; y 11) estocástica, que cambia a lo largo del tiempo de forma desconocida.
Los modelos estocásticos de volatilidad permiten modelar el comportamiento de la serie en estudio y predecir su comportamiento futuro con mayor precisión, se argumenta a favor:
Miden los cambios de volatilidad de la serie en el tiempo.
Proporcionan mejores estimaciones locales de la volatilidad.
Capturan el agrupamiento de la volatilidad en el tiempo.
Permiten estudiar la persistencia de la volatilidad.
Facilitan las realizaciones de la volatilidad a corto plazo.
Existen diferentes modelos estocásticos de volatilidad, que con sus ventajas y desventajas forman una gama impresio nante de herramientas disponibles para el modelado de series de tiempo.
Si bien, no es para nada despreciable el esfuerzo realizado por los investigadores que desarrollaron los modelos de volatilidad histórica y la metodología Box-Jenkins, son ampliamente conocidas las desventajas de dichos métodos. Estos modelos hablan de la estructura de la media condicional de los datos, el supuesto de varianza constante y la linealidad de dichos modelos hacen que se limite el estudio de algunas series temporales o se obtengan conclusiones erradas, viéndose afectada la eficiencia de los parámetros estimados. Es por esta razón que surgen en la década de los 80 una serie de modelos que se enfocan en estudiar los momentos condicionales de segundo orden de las series de tiempo10, conocidos modernamente como la familia de modelos autorregresivos condicionales heterocedásticos. En la Tabla 3 se encuentran los principales modelos de esta familia y en la Tabla 4 sus principales características.
Tabla 4 Características de los principales modelos de la familia ARC
| Modelo | Características |
|---|---|
| Modelo autorregre-sivo condicional heterocedástico [ARCH (q)] | Fue el primer modelo formal que estudió el comportamiento de la varianza de una variable con respecto al tiempo. Las características más sobresalientes de un modelo ARCH(p) son: i) las esperanzas incondicional y condicional del proceso son nulas; 11) la varianza incondicional es constante; 11i) la varianza condicional no es constante, depende de los valores pasados de la variable de estudio al cuadrado, es en sí misma un proceso autorregresivo (AR) que genera errores heterocedásticos, condicionados por la varianza del error de periodos pasados; iv) los errores estocásticos de la serie no presentan autocorrelación a nivel, pero no son independientes porque se relacionan mediante sus varianzas; v) la estructura ARCH del término de error y la estructura AR de la serie interactúan entre sí. Un shock grande en yt se asocia con una varianza persistentemente grande de los errores; a mayor valor del coeficiente at mayor será la persistencia. Mientas más alejada esté la serie yt de su media, mayor es su varianza y vi) la distribución incondicional de un proceso ARCH tiene forma desconocida. Pero, se asegura que tiene colas más gruesas que las de una distribución normal, por ello es leptocúrtica. En lo que respecta a la estimación de los parámetros de un modelo ARCH, tal como lo planteó Engle, se realiza mediante el método de máxima verosimilitud (MV). |
| Modelo generalizado autorre-gresivo condicional heterocedástico [GARCH (p,q)] | Es una ampliación del modelo ARCH de Engle debido a las dificultades de estimación que este presenta cuando se aplica a estructuras dinámicas de los cuadrados de las series, porque se impone una estructura fija de rezagos. Esto implica que para estimar un ARCH se necesita una estructura de rezagos muy larga de la varianza condicional para modelar la memoria de los datos, hecho que genera una gran pérdida de grados de libertad. El aporte de Bollerslev es fundamental en el desarrollo de los métodos de modelado de series de tiempo univariantes, porque fortalece la utilidad del modelo ARCH. El modelo GARCH (p,q) permite capturar la memoria larga de la serie y posee una estructura de rezagos más flexible. Un modelo GARCH se destaca porque: i) rt es un proceso estocástico estacionario idénticamente distribuido con media cero y varianza unitaria, es decir, es un ruido blanco; 11) la función de distribución marginal no es conocida pero se pueden calcular los primero dos momentos del proceso; 11i) el proceso Et es estacionario; iv) en los momentos condicionales, en t, el valor de t-1 es una realización concreta conocida (no aleatoria); v) la varianza condicional de las perturbaciones de la serie original constituyen un proceso ARMA, expresado por ht y vi) los modelos GARCH son más parsimoniosos que los modelos ARCH con q grande, lo que los hace más fáciles de identificar y de estimar. Bollerslev en su artículo definió el término de la varianza condicional introducido en la ecuación [5] como un mecanismo de aprendizaje adaptativo de un ARCH(oo). La estimación de los parámetros de un modelo GARCH(p,q) se realiza por el método de MV. Para encontrar los estimadores MV Bollerslev (1986) sugirió el uso de un algoritmo iterativo como el algoritmo de Berndt, Hall, Hall y Hausman de 1974 (BHHH) y no el propuesto por Engle (1982), por la complejidad y la no seguridad de convergencia. En 1992 Bollerslev y Wooldrige propusieron una estimación cuasi máximo verosímil (CMV). |
| Modelo generalizado autorre-gresivo condicional heterocedástico Integrado (IGARCH) | Puede considerarse una variante entre un ARCH(q) y un GARCH(p,q) cuya característica principal es estimar la varianza partiendo del hecho de que esta es integrada en varianza. En los modelo IGARCH la información existente en el momento t es sumamente importante para realizar predicciones óptimas en cualquier momento t+s de interés. El efecto sobre ht+s de ht+1 a medida que s co es cada vez menor pero nunca nulo, por lo que el efecto de la varianza persiste sobre el modelo. Engle y Bollerslev encontraron que la distribución de la varianza del error estocástico presentaba una cola superior a la de una distribución normal, asumida para explicar los modelos descritos en apartados anteriores. Ellos descubrieron que la verdadera distribución que sigue la varianza es una t-student estandarizada La estimación por MV de los modelos ARCH y la cuasi máximo verosímil de los GARCH son perfectamente aplicables a los modelos IGARCH. |
| Modelo generalizado autorre-gresivo condicional heterocedástico ex ponencial [EGARCH (p,q)] | En 1987 Milhoj propuso un modelo ARCH logarítmico, debido a las dificultades encontradas al estimar el modelo ARCH porque los coeficientes resultaban negativos. El modelo de la ecuación [8] no requiere condiciones para asegurar que la varianza condicional sea positiva, pero una limitación es que la varianza condicional ht es simétrica en los valores pasados, por ende no pondera de forma correcta la volatilidad asociada. Nelson (1991) estudió los modelos ARCH y GARCH, y concluyó: i) las condiciones impuestas sobre los parámetros del modelo para asegurar la positividad de la varianza condicional frecuentemente son incumplidas. Además, parámetros siempre positivos generan estimaciones incorrectas por el efecto creciente que permanece en la estimación, lo que evita la posibilidad de predecir un comportamiento oscilatorio; 11) el modelo GARCH tiene incapacidad para modelar la asimetría de la volatilidad asociada a las altas y bajas asociadas a la serie, porque la función de varianza condicional simétrica es inapropiada puesto que no sería capaz de representar la correlación negativa entre la volatilidad y los datos pasados; 11i) refiriéndose a los modelos ARCH, Nelson (1991) declara que tienen la debilidad de no poder medir la persistencia de un shock pasado sobre los valores de la varianza condicional, por lo que si este impacto es persistente pasaría a formar parte de la estructura temporal de la serie (Poterba & Summers, 1986). No medir adecuadamente su impacto altera las decisiones asociadas. |
| Modelo generalizado autorre-gresivo condicional heterocedástico con umbral [TGARCH (p,q)] | Zakoian, en 1990 llegó a derivar una clase de modelos en donde el interés residía sobre la desviación estándar condicional. Al modelo descrito en [10] lo denominó el "threshold ARCH" (TARCH), debido a que el coeficiente et cambia cuando cruza el umbral del cero. Cuando s-1 > 0, Vht es lineal cuya pendiente es a+ ; por el contrario si e < 0, Vht sigue siendo lineal pero la pendiente es a . Es precisamente esta característica la que permite la asimetría en la varianza condicional, comportamiento similar al del modelo EGARCH. Zakoian realizó una extensión de su modelo añadiendo las desviaciones estándar condicionales pasadas como variables explicativas. |
| GJR-GARCH | Los investigadores Glosten, Jagannathan y Runkle (1993), basados en los modelos descubiertos hasta ese momento, desarrollaron un modelo ARCH para comprobar ciertas características de los mercados bursátiles, específicamente. Suponiendo que el modelo sigue una estructura ARCH, en donde el presente se alimenta de información pasada, genera dos tipos de errores: uno propio del modelo y otro propio del método de estimación. El modelo GJR-ARCH tiene tres características fundamentales: i) asimetría en la respuesta de la variable ante las buenas y malas noticias. Las malas noticias generan con frecuencia mayor volatilidad en la serie; 11) la volatilidad en los mercados bursátiles es inversamente proporcional a la prima de riesgo de estos y 11i) patrones estacionales en el comportamiento de la serie hacen que se pueda modelar la misma incluyendo variables ficticias. |
| AP-ARCH (p,q) | En 1993, Ding, Granger y Engle, basados en características que ellos encontraron comunes en las series de tiempo financieras, propusieron: i) no solo existe autocorrelación entre los valores de la perturbación estocásticas en términos absolutos, sino que esa perturbación elevada a una potencia "d", muestra mayores autocorrelaciones; 11) no existen razones suficientes para admitir, desde un principio, la relación lineal en la especificación de la varianza de los modelos de la familia ARCH, respecto a los errores rezagados al cuadrado o a la desviación estándar rezagada y 11i) como la autocorrelación observada en las series financieras, evidencia ser mayor en los valores cercanos a la unidad, no resulta correcto usar la varianza o la desviación estándar, sino que un valor de esta última elevado a una potencia "8", que será determinada. |
| Nota: existen otros modelos estocásticos de volatilidad como el LGARCH, que es una linealización del GARCH-M, MGARCH consiste en especificar la varianza de forma multiplicativa, FACTOR ARCH que emplea la covarianza entre varias series temporales, modelos ARCH de régimen cambiante, el Q-GARCH que es un modelo GARCH cuadrático, y las diferentes variantes de los modelos ARCH y GARCH multivariante, pero no serán tratados en este estudio. |
METODOLOGÍA
Este estudio es de carácter descriptivo-explicativo. Descriptivo porque busca detallar un fenómeno económico en una circunstancia temporal y geográfica deter minada. Explicativo, ya que su finalidad es exponer el comportamiento de una variable, en este caso el tipo de cambio paralelo mediante el uso de modelos estadísticos; requiere de control tanto metodológico como estadístico. La inves tigación es documental, "aquella que se basa en la obtención y análisis de datos provenientes de materiales impresos u otro tipo de documentos" (Arias, 2006).
Los datos: se toma como fuente de datos la serie correspondiente al dólar paralelo con referencia al "dólar Cúcuta", entre el 3 de enero de 2005 y el i de enero de 2016, con operaciones durante cinco días a la semana, por lo que sábados y domingos no están incluidos. Conformada por 2869 observaciones.
Haciendo referencia a la Figura i, el comportamiento al alza de la serie puede explicarse, en parte, por el exceso de trabas burocráticas para el acceso a dólares oficiales, que por ley natural del mercado, ante escasez de oferta y exceso de demanda, impulsa el aumento del precio. Tal como era de esperarse, por ser una serie financiera, el tipo de cambio paralelo es leptocúrtica. En la Tabla 5 se detallan las estadísticas descriptivas del tipo de cambio paralelo.
Tabla 5 Estadísticas descriptivas del tipo de cambio paralelo de Venezuela 2005-2015
| Min. | 1stQu. | Median | Mean | 3rdQu. | Max. | Var | SD | Asimetría | Curtosis | Obs. |
|---|---|---|---|---|---|---|---|---|---|---|
| 2,51 | 4,10 | 7,92 | 63,81 | 23,20 | 920,60 | 28260,9 | 168,10 | 3.636 | 12.61 | 2869 |
Fuente: elaboración propia con base en datos dólar Cúcuta.
Se concluye para siete de siete pruebas, como se muestra en la Tabla 6, que el tipo de cambio paralelo de Venezuela no se ajusta a una distribución normal. Este problema se trató de corregir a través de transformaciones en logaritmo, la diferencia y los rendimientos, sin mayores resultados, aun cuando este último permite evidenciar la volatilidad de la serie, como se aprecia en la Figura 2 y en la Tabla 7.
Tabla 6 Pruebas de normalidad del tipo de cambio paralelo
| Estadístico | Valor | P-value |
|---|---|---|
| Shapiro-Wilk | W = 0,39755 | < 2,2e-16 |
| Jarque Bera | X-squared = 25389 | < 2,2e-16 |
| Anderson-Darling | A = 699.23 | < 2,2e-16 |
| Cramer-von Mises | W = 141.98 | 7.37E-10 |
| Pearson | P=37361 | < 2.2e-16 |
| Lilliefors (Kolmogorov-Smirnov) | D = 0.35769 | < 2.2e-16 |
| Shapiro-Francia | W = 0.39744 | < 2.2e-16 |
Fuente: elaboración propia con base en datos dólar Cúcuta. a = 5%.
Tabla 7 Pruebas de normalidad de las transformaciones del tipo de cambio paralelo
| Logaritmo TCP | Diferencia TCP | Rendimientos TCP | |||||
|---|---|---|---|---|---|---|---|
| Estadístico | Valor | P-value | Valor | P-value | Valor | P-value | |
| Shapiro-Wilk | W=0,83252 | < 2,2e-16 | W=0,22728 | < 2,2e-16 | W=0,73022 | < 2,2e-16 | |
| Jarque Bera | X=849,07 | < 2,2e-16 | X=3546500 | < 2,2e-16 | X=164280 | < 2,2e-16 | |
| Anderson-Darling | A=170,2 | < 2,2e-16 | A=810,05 | < 2,2e-16 | A=810,05 | < 2,2e-16 | |
| Cramer-von Mises | W=3i,349 | 7,37E-10 | W=173,7 | 7,37E-10 | W=35,538 | 7,37E-10 | |
| Pearson | P=3845,9 | < 2,2e-16 | P=55020 | < 2,2e-16 | P=4942,7 | < 2,2e-16 | |
| Lilliefors (Kolmogorov -Smirnov) | D=0,24852 | < 2,2e-16 | D=0,40234 | < 2,2e-16 | D=0,16559 | < 2,2e-16 | |
| Shapiro-Francia | W=0,83297 | < 2,2e-16 | W=0,22501 | < 2,2e-16 | W=0,72737 | < 2,2e-16 | |
Fuente: elaboración propia con base en datos dólar Cúcuta. a = 5%.
En consecuencia, se decidió trabajar con los rendimientos del tipo de cambio paralelo (RTCP), porque tienen propiedades deseables para su modelado. Dicha serie, construida a partir de la expresión [17], obedece a la literatura consultada:
RCTP = [log(TCPt ) - log(TCPt-i )] * 100 [17]
La serie RTCP no se distribuye normal, presenta un fuerte apuntamiento y resulta estacionaria en media. Adicionalmente, no es independiente y está correlacionada, según los resultados del test de independencia de Brock, Dechert y Scheinkmanes (BDS), es decir, no es ruido blanco, como se confirma en la Tabla 8 y en la Figura 3.
Tabla 8 Estadísticas de los rendimientos del tipo de cambio paralelo de Venezuela, 2005-2015

Fuente: elaboración propia con base en datos dólar Cúcuta. a = 5%.
Así, los rendimientos del tipo de cambio paralelo concuerdan con las características planteadas por Mandelbrot (1963) y Fama (1963) para las series financieras:
Concentración de los datos en torno a la media.
Distribución leptocúrtica (apuntamien to de las observaciones).
Colas gruesas de la distribución, aunque no muy evidente.
En concreto se estiman modelos ARCH, GARCH, EGARCH, GJR-GARCH y AP-ARCH para el tipo de cambio paralelo, siguiendo la metodología de sus autores, descrita anteriormente.
Los modelos: el método de estimación de los parámetros de interés que se usa es el de máximo verosimilitud (MV) para los modelos ARCH y AP-ARCH,
haciendo caso a la afirmación de diversos autores (Engle, Bollerslev, Nelson, entre otros) que es un método asintóticamente superior al método de mínimos cuadrados (MCO), por lo que logra estimadores eficientes, dada la ausencia de linealidad11.
Los modelos GARCH, EGARCH y GJR-GARCH se estiman mediante el método de cuasi máximo verosimilitud (CMV), usado con menos frecuencia que el MV, pero empleado cuando no se cumple el supuesto de normalidad de las variables en estudio12.
El algoritmo utilizado para estimar los modelos es el Berndt, Hall, Hall y Hausman (BHHH, 1974). Este, a diferencia de los métodos de estimación tradicional que asumen linealidad en variables y parámetros, supone la existencia de relación no lineal en ambos, parámetros y variables13, además de garantizar la convergencia de los valores estimados.
En cuanto al software, el procesamiento de los datos y la estimación de los modelos se realiza con The R Project for Statistical Computing, versión 3.3.i, los programas, modificados, se basan en los suministrados por el sitio web y las librerías electrónicas asociadas.
RESULTADOS Y DISCUSIÓN
En concreto, dadas las consideraciones del marco teórico, se procedió a estimar los modelos, se concentró el trabajo en la rama de los modelos no lineales (modelos de la familia ARCH). Después de esto, se observaron los siguientes resultados:
Examinados los cuadros de los rendimientos del tipo de cambio paralelo14, Figura 4, estos concordaron con los hallazgos hechos por Ding et al. (1993) sobre el índice S&P 500:
Tendencia creciente de la serie sin transformar, acentuada al final del periodo, producto de la alta volatilidad.
Los rendimientos del tipo de cambio paralelo eliminan la tendencia, porque se distribuye de manera estable en torno a la media que es 0,1996.
El valor absoluto de los rendimientos refleja el carácter volátil de la serie, confirmando la persistencia de esta o los conglomerados de volatilidad que exponían Mandelbrot (1963) y Engle (1982).
La estructura de autocorrelación de la serie ajustó a través de un proceso de autocorrelación de orden uno, como lo estimaran Ding et al. en 1993. En la Tabla 9, los valores negativos de los coeficientes de autocorrelación reflejaron la recuperación de los rendimientos, que se conoce en la literatura como "recuperación de beneficios o reversión media". En el caso de los rendimientos al cuadrado y sus valores absolutos se cumplió que son todos estadísticamente significativos, este hecho puso de manifiesto dos cosas:
La existencia de una memoria larga en la serie.
La persistencia temporal de la volatilidad asociada, es decir, presencia de conglomerados de volatilidad.
Tabla 9 Autocorrelaciones de los rendimientos del tipo de cambio paralelo

Fuente: elaboración propia con base en datos dólar Cúcuta; srtcp: rendimientos al cuadrado; artcp: rendimientos absolutos.
La presencia de estructuras no lineales en la serie se confirmó con las pruebas linealidad mostradas en la Tabla 10 y con la estimación de un modelo de regresión lineal, que incluyó una estructura promedio móvil de orden uno [MA(1)] de la forma

mediante MCO, se estudiaron los residuos estimados y como se aprecia en la Tabla 11, existían efectos ARCH en los residuos de dicho modelo15.
Tabla 11 Estimación de efectos ARCH

Fuente: elaboración propia con base en datos dólar Cúcuta. a=50%. Prob: probabilidad. Q: estadístico Ljung- Box.
Los modelos de la familia ARCH, mostrados en la Tabla 12, fueron los modelos estimados en este documento; todos ajustaron mediante una distribución t-Student. Los parámetros de cada uno de ellos son estadísticamente significativos y los residuos resultaron ser ruido blanco no gaussiano (ver Apéndice n." 1), por lo que, concretamente, todos ellos modelan correctamente el comportamiento de los rendimientos del tipo de cambio paralelo de Venezuela. De los modelos de esa tabla, el mejor modelo fue el ARMA (2,1) - EGARCH (1,1), afirmación hecha con base en los criterios de información de Akaike (1974), Schwarz (1978), Shibata (2002) y Hannan-Quinn (1979), pues, reportaron los menores valores de todos los modelos. La ecuación de la varianza representada por la ecuación [18], estimada del modelo seleccionado, presentó los signos esperados:
En la ecuación [18], 0,91793 reflejó la persistencia, la volatilidad de la varianza que, según Nelson (1991), forma parte de la varianza heterocedástica. Coeficiente muy cercano a la unidad, en este modelo se expresó por 0,91793 log(ht-i), lo que significa que el valor estimado de la varianza en el tiempo t, arrastra casi por completo la variabilidad del periodo anterior, t-1. El efecto asimétrico propio del método, el apalancamiento, fue 0,13530; así, ante una innovación negativa rezagada un periodo, el resultado sobre el logaritmo de la varianza estimada es positivo, mientras que resulta nulo si la innovación referida es positiva. Un choque negativo aumenta la volatilidad, mientras que un choque positivo disminuye la volatilidad. En el caso específico de los rendimientos del tipo de cambio paralelo, un choque negativo se asocia a una depreciación del bolívar frente al dólar, y por el contrario, un choque positivo refiere a una apreciación del mismo.
Se consideró un buen ajuste de la varianza condicional del modelo, como lo reflejó el gráfico (c), de la Figura 5; la varianza estimada replicó correctamente el comportamiento de la volatilidad del tipo de cambio paralelo, como era de esperar. El correlograma cruzado, gráfico (g), entre las observaciones reales y sus cuadrados, ajustó dentro de las bandas, confirmando su aleatoriedad.
La curva de impacto de innovaciones ratificó el efecto asimétrico del modelo EGARCH estimado, gráfico (1) de la Figura 5. Sin embargo, es inconsistente con lo expresado en la ecuación [18], según la afirmación de Nelson (1991), porque el efecto asimétrico que muestra la curva de impacto de innovaciones es positivo para innovaciones positivas y es levemente negativo para innovaciones negativas. Este hecho se podría justificar en la existencia de un cambio de signo en el modelo estimado, que provoca efectos contrarios según el signo de la innovación, pero empíricamente no tiene sentido, porque de ser cierto, una depreciación del tipo de cambio paralelo traería una menor volatilidad, y una apreciación del tipo de cambio estaría relacionada con una mayor volatilidad, y es ampliamente conocido que de esa forma no opera el mercado paralelo de divisas.
Tabla 12 Síntesis de los modelos de la familia ARCH estimados

Fuente: elaboración propia con base en datos dólar Cúcuta. . AIC: criterio de Akaike. BIC: criterio de Schwarz. S: criterio de Shibata. HQ: criterio de Hannan-Quinn
Fuente: elaboración propia con base en datos dólar Cúcuta. α = 5%
Incluso dentro de la formación contemporánea de economistas a nivel mundial o asimismo en posgrados relacionados, se ha otorgado mayor importancia al segundo en desmedro del primero. Sin embargo, este será un debate que tendremos que dar desde la academia.
Los parámetros estimados del modelo ARMA (2,1) - EGARCH (1,1) resultaron no ser estables en conjunto, según el test de Nyblom. Este test prueba la estabilidad simultánea de todos los parámetros, garantiza un buen ajuste para modelos no lineales, deriva un estadístico basado en el multiplicador de Lagrange. La hipótesis nula que maneja es similar a la planteada por el test de estabilidad paramétrica de Chow (Ho: todos los parámetros son estables en conjunto). Para el caso del modelo estimado, como se observa en la Tabla 13, el valor calculado del estadístico es mayor que su valor tabulado, garantizando que no hay estabilidad paramétrica conjunta, es decir, los parámetros estimados cambian a lo largo del tiempo, hecho esperado dada la elevada volatilidad de la serie modelada.
En lo que respecta a la estabilidad individual de los parámetros, según el test de Hansen, no todos los parámetros estimados son estables individualmente. La hipótesis nula que maneja el test es que βi 16 es constante (Ho: βi es contante; para 1=1,2,... ,k). En la Tabla 13 se puede apreciar que los parámetros asociados al modelo ARMA (2,1) de la media sí son estables, en tanto, los correspondientes al modelo EGARCH (1,1) no lo son: a0 que representa la mínima varianza, ai que representa el efecto apalancamiento y βi que representa la persistencia del modelo no son estables, pero γ1 asociado al término autorregresivo del error (Nelson, 1991), sí es estable. Este último hecho infiere que, además de ser elevada la persistencia del modelo, esta no es constante y cambia en función del signo de la innovación, arrastrando fuertemente la variabilidad del periodo t-1 al periodo t. Confirmándose la existencia de conglomerados en la serie, como expone la teoría.
Es importante destacar que estos dos test, Nyblom y Hansen, tienen características similares: i) son fáciles de calcular y son robustos para heterocedasticidad; 11) al igual que el test de Chow, ninguno suministra información sobre el punto de quiebre del parámetro; 11i) la distribución del estadístico no es estándar y obedece al valor de k (número de parámetros estimados), generalmente bajo la hipótesis nula la distribución utilizada es la de Cramer-Von Mises, pero su elección depende de la variable de interés, si es estacionaria o no, o si tiene tendencia determinística y iv) los valores tabulados, para el contraste de hipótesis, fueron calculados por simulación y están codificados en los artículos seminales de los autores.
Tabla 13 Test de estabilidad y sesgo de signo del modelo EGARCH estimado
| Test de Nyblom | |||||
|---|---|---|---|---|---|
| Valor calculado | Valor tabulado | Conclusión | |||
| Estadístico conjunto | 8,01 | 2,11 | No Estables | ||
| Test de Hansen | |||||
| Valor calculado | Valor tabulado | Conclusión | |||
| AR(I) | 0,1525 | 0,47 | Estable | ||
| AR(2) | 0,3075 | 0,47 | Estable | ||
| MA(I) | 0,1674 | 0,47 | Estable | ||
| «0 | 1,7801 | 0,47 | No estable | ||
| «I | 0,8326 | 0,47 | No estable | ||
| Pl | 1,4276 | 0,47 | No estable | ||
| 0,2122 | 0,47 | Estable | |||
| shape | 2,8515 | 0,47 | No estable | ||
| Test de sesgo de signo | |||||
| Probabilidad | Conclusión | ||||
| Sesgo en el signo | 0,1121 | No significativo | |||
| Sesgo positivo | 0,9103 | No significativo | |||
| Sesgo negativo | 0,2817 | No significativo | |||
Fuente: elaboración propia con base en datos dólar Cúcuta. a=5%.
En la Tabla 13 también se pueden apreciar los resultados correspondientes al test de sesgo de signo y tamaño. Implica que la varianza condicional depende de forma simultánea del signo y del tamaño de la innovación. En el modelo EGARCH(1,1) estimado, no se encontró evidencia signi ficativa sobre este tipo de relación en la varianza condicional del modelo estima do, la probabilidad asociada es mayor al nivel de significancia seleccionado. Por ende, el efecto asimétrico sobre la varianza depende del signo de la innovación pero no de su tamaño.
Fuente: elaboración propia con base en datos dólar Cúcuta.
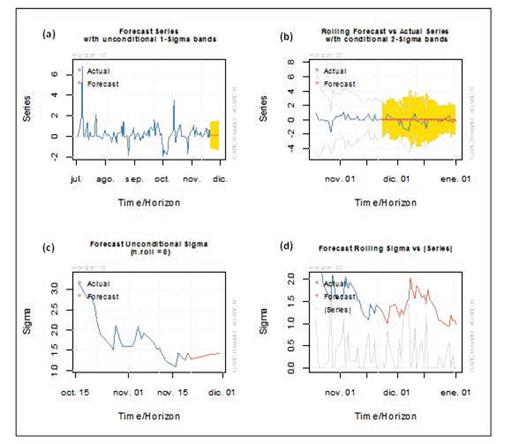
Finalmente, en cuanto a la bondad en la predicción del modelo, se estimó el modelo dejando 30 observaciones por fuera para hacer los pronósticos. En la Figura 4 se observa que si bien el modelo cumplió con todos los supuestos de validación, sus predicciones no resultaron ser las mejores. En el gráfico (b) de la Figura 6 existe marcada diferencia entre los primeros valores predichos de los rendimientos del tipo de cambio paralelo, a pesar de que, a medida que avanzaba el horizonte temporal, el pronóstico se asemejaba al valor observado de la serie. En el gráfico (d) de la figura referida, la varianza pronosticada no se acercó al valor absoluto de la serie, contradiciendo el pronóstico, el carácter volátil de la serie.
CONCLUSIONES
Con el fin de modelar el tipo de cambio paralelo de Venezuela entre 2005 y 2015, desde el enfoque de los modelos estocásticos de volatilidad, se realizó una descripción de la variable de interés, considerada una variable próxima al valor real del tipo de cambio paralelo. Se especificó que esta no puede ser utilizada directamente en el proceso de estimación porque no cumple con las características teóricas establecidas. Se construyó la variable rendimientos del tipo de cambio paralelo que representa, con mayor precisión, el carácter volátil de la serie original.
En concreto, se identifica que la volatilidad de los rendimientos del tipo de cambio paralelo de Venezuela tiene comportamiento asimétrico, indica que las devaluaciones de la moneda venezolana, producto de las decisiones de política cambiaria, generan un fuerte choque negativo sobre el mercado paralelo de divisas, incrementando la volatilidad del precio del dólar en dicho mercado, como era lo esperado.
En lo que respecta a los modelos estimados, y a la serie de tiempo estudiada, puntualmente se puede decir:
Los modelos ARIMA no sirven para estimar el comportamiento de los rendimientos del tipo de cambio paralelo debido a la alta volatilidad de la serie, ya que la estructura presente en la serie es no lineal.
Si bien es cierto que los modelos de la familia ARCH son los adecuados para estimar la variable rendimientos del tipo de cambio paralelo, los modelos utilizados en este estudio no predicen correctamente más de dos observaciones, por lo que no pueden ser empleados como referencia para decisiones relativas a política cambiaria.
Es importante destacar del párrafo anterior que, a pesar de que los modelos de la familia ARCH no logran predecir los valores de la serie, sí logran modelar correctamente la variable estudiada.
Como era de esperar, por lo sugerido en la teoría, el modelo que mejor ajustó fue un modelo EGARCH(1,1). Se confirmó que las series financieras y cambiarias, de alta volatilidad, se modelan mejor cuando se considera la presencia de efectos de apalancamiento.
El tipo de cambio paralelo de Venezuela entre los años 2005 y 2015, desde el enfoque de las series de tiempo, resulta ser una variable compleja para su modelado. Hecho causado por los factores involucrados en su cálculo; el principal de ellos la incertidumbre, que no es medible directamente, pero que está asociada al incremento del precio del dólar estadounidense en términos del bolívar.
En función de lo antes expuesto se recomienda:
Cambiar la forma de cálculo de la variable estudiada, porque la estima ción del precio del bolívar venezolano en términos del peso colombiano en la frontera no se hace con ninguna rigurosidad estadística, a diferencia de sus otros dos componentes, la oferta monetaria (M2) y las reservas internacionales de Venezuela, que es información tomada de un ente oficial. Esto con el fin de capturar el verdadero comportamiento de la variable.
Realizar estimaciones con los modelos de la familiar ARCH no empleados en este estudio, para contrastar su ajuste y determinar si existe superioridad de alguno de ellos.
Formalizar estimaciones de modelos de volatilidad estocástica (SV) mediante métodos bayesianos, que precisen el efecto sobre el precio del dólar de variables no observadas.
Utilizar técnicas multivariantes de análisis de volatilidad para tener mejores opciones en el momento del modelado.
Dado el crecimiento de la liquidez monetaria y la persistente volatilidad del tipo de cambio paralelo, se sugiere probar la hipótesis del overshooting para la economía venezolana.