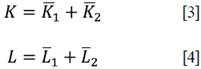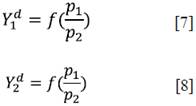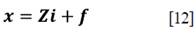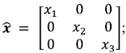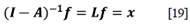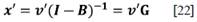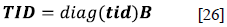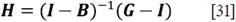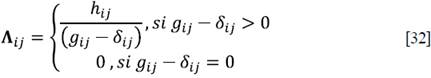INTRODUCCIÓN
Los impuestos son una de las principales herramientas de la política fiscal. Son un instrumento que está sometido a una enorme polémica, ya que, en esencia, una parte de la renta percibida por los agentes económicos (consumidores y firmas) pasa a manos del Gobierno. El papel básico de una estructura tributaria consiste en contribuir al desarrollo económico, lo que puede ser contradictorio, al menos para los países de Latinoamérica (LATAM), debido a las altas tasas de desigualdad y sobre todo a la corrupción que existe en las esferas de la administración pública (Ivanyna et al., 2018).
La evolución de la estructura tributaria en LATAM ha sido particularmente interesante. Al seguir la nomenclatura de la OCDE, se pueden clasificar cinco tipos de impuestos: impuestos sobre la renta, utilidades y ganancias de capital (IMPORRENTA); contribuciones a la seguridad social (CSS); impuesto sobre la nómina (IMPOLABOR); impuestos a la propiedad (IMPOPROP); impuestos a bienes y servicios y otros impuestos1 (OCDE, 2019, p. 2). Para 1990, del recaudo total de los países de la región, el IMPORRENTA era del 20.1 %, mientras que en el 2017 fue de 27.1 %; las CSS pasaron de representar el 13.1 % al 16.9 %; el IMPOLABOR pasó del 0.4 al 0.7 %; el IMPOPROP se ha mantenido relativamente estable a lo largo del tiempo, al pasar del 3.9 % al 3.4 %; el IVA aumentó del 15.6 a casi el 28 %.
El caso de Colombia se caracteriza porque entre el período 1984-2016 se han realizado al menos 16 reformas tributarias2, de las cuales una se llevó a cabo entre 1986 y 1990 (Ley 75); entre 1990-2000 se aprobaron seis proyectos de ley; entre el 2000 y el 2010 se aprobaron cinco, y entre el 2010 y el 2016 se aprobaron otros cinco. En ese mismo período, el IMPORRENTA con respecto al recaudo total aumentó 3 puntos porcentuales (PP), pasó del 29.9 % al 33.1 %, mientras que las CSS, IMPOLABOR e IMPOPROP pasaron de 4.3 % a 1.8 %, de 7.9 % a 7.7 % y de 2.2 % a 10.3 %, respectivamente. El IVA aumentó de 22.6 % a 29.1 %.
Lo anterior indica que a pesar de que el recaudo en LATAM y Colombia ha aumentado, este se encuentra altamente concentrado, ya que la mayor parte del recaudo se da en los impuestos indirectos, mientras que las empresas son las que pagan principalmente los impuestos directos. Como indican Concha et al. (2017, p. 6), "(...) el efecto distributivo del impuesto sobre la renta es reducido en comparación con países de la región: en la tributación a las empresas existen importantes desigualdades sectoriales, verticales y horizontales, y se ha encontrado regresividad en el IVA".
En la literatura económica los impuestos tienen un papel muy bien definido: financiar los niveles de gasto público. No obstante, y la configuración de las cuentas gubernamentales así lo indican, los Estados deben recurrir al endeudamiento debido a la falta de pago de los contribuyentes3. Una estructura impositiva mal definida, regresiva por configuración, permite que el efecto de los impuestos pueda recaer en los agentes que no se desea gravar, como lo indican Concha et al. (2017). Es decir, la propagación de los efectos tributarios está influenciada no solo por el diseño institucional concurrente, sino por las relaciones intersectoriales de la economía.
El efecto de los impuestos ha sido estudiado desde una perspectiva de la descentralización del gasto (Bonet-Morón et al., 2018; Bonet, 2006; Falleti, 2006; Olivera & Zuluaga, 2014; Restrepo, 2004), asuntos ambientales (Velásquez, 1998), disciplina fiscal (Botero & García, 2018; Ciro & De Mendonça, 2017; Rodríguez, 2014) y crecimiento económico (Botero et al., 2013; Chamorro & Urrea, 2016; González et al., 2014; López-Vera et al., 2018; Páez, 2011; Romero, 2017). Son escasos los estudios relacionados con los efectos de los impuestos en los sectores.
Con base en lo anterior, el objetivo del presente escrito es ilustrar los efectos de propagación de los impuestos directos e indirectos sobre los sectores de la economía. El documento está organizado así: la primera parte consta de esta corta introducción, la segunda presenta los aspectos teóricos y la revisión de literatura, la tercera expone el marco teórico, la cuarta, la metodología, la quinta sección describe los principales resultados y la sexta sección presenta las conclusiones.
ASPECTOS TEÓRICOS Y UNA BREVE REVISIÓN DE LA LITERATURA
Como el objetivo del presente escrito consiste en evidenciar el efecto de un sector sobre otros, se parte de un modelo de dos sectores de Harberger (1962). Este modelo permite analizar el traspaso de los impuestos.
Se inicia con una economía con dos sectores (Y1, Y2), con ofertas de mano de obra
 y capital
y capital
 fijas4. Se suponen rendimientos constantes a escala (RCE) en ambos sectores con pleno empleo en ambos factores de producción, sin costos asociados a la movilidad entre factores. Tenemos entonces:
fijas4. Se suponen rendimientos constantes a escala (RCE) en ambos sectores con pleno empleo en ambos factores de producción, sin costos asociados a la movilidad entre factores. Tenemos entonces:
La economía se enfrenta a las siguientes restricciones5:
Como no existen costos entre los sectores, el valor de la productividad de los factores queda definida como:
Luego, las demandas6 para cada sector son:
Con lo anterior se obtiene un sistema de 10 ecuaciones y 10 incógnitas (K¡, Li, Pi, Yi, Wi, r¡). Sea la т la tasa impositiva en el sector 2 sobre el capital
 y dado que L y K son fijos con precios de w y r, respectivamente, se tiene que el cambio en los impuestos afecta los precios de los factores, mientras que
dw/d
т y
dr/d
т y describe como se da el cambio del capital a la mano de obra, mientras que
dp
1
/dт y
dp
2
/dт muestran como el cambio de los impuestos pasa del sector 2 al sector 1.
y dado que L y K son fijos con precios de w y r, respectivamente, se tiene que el cambio en los impuestos afecta los precios de los factores, mientras que
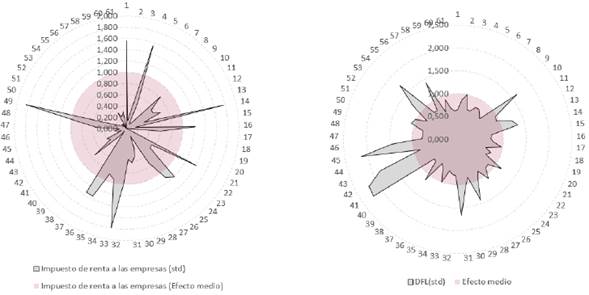
dw/d
т y
dr/d
т y describe como se da el cambio del capital a la mano de obra, mientras que
dp
1
/dт y
dp
2
/dт muestran como el cambio de los impuestos pasa del sector 2 al sector 1.
En este punto, resulta conveniente explicar las ideas intuitivas del modelo de Harberger (1962):
Los impuestos en el capital del sector 2 aumentan el precio del capital para este sector, lo cual hace que la demanda agregada por capital (K) disminuya, ya que las cantidades de los factores de producción de capital (K) y mano de obra (L) son fijas (efecto sustitución).
Lo anterior implica que el capital en el sector 2 será más costoso en términos relativos y la demanda de bienes irá al sector 1.
Si la relación de capital-trabajo del sector 1 es menor que la relación capital-trabajo del sector 2, entonces el sector 1 será menos capital-intensivo y la demanda agregada por capital disminuirá.
Si la relación de capital-trabajo en sector 1 es mayor que la relación de capital-trabajo que el sector 2, entonces el sector 1 será más capital-intensivo y la demanda por capital aumentará.
Modelo insumo-producto, multiplicadores tributarios7
La matriz insumo-producto (en adelante MIP) es una representación de las interrelaciones sectoriales de un sistema económico a partir de la compra/venta de bienes y servicios intermedios y/o finales en un área geográfica determinada, la cual pueden ser países, regiones, ciudades, territorios, entre otros. Independientemente del tipo de área que se esté manejando, es importante tener presente que debe haber una subdivisión en sectores económicos "debidamente" clasificados; se hace énfasis en "debidamente", ya que el marco de clasificación común son las cuentas nacionales; no obstante, si el área es muy pequeña (< 10 000 habitantes8) se debería pensar en una clasificación más pertinente y coherente con las actividades predominantes.
En la MIP, cada sector económico juega un papel doble: un sector puede actuar como vendedor (sector i) o comprador de bienes intermedios de otro sector (sector j), esto es, el sector j compra de otros sectores relacionados a su cadena de producción. Por ejemplo, la industria automovilística demanda insumos de la industria del acero; la industria de pan demanda trigo; la industria de muebles de madera demanda madera, y así sucesivamente. Si se suponen n sectores de la economía y que la producción de un sector (x i ) puede ser distribuida a través de las ventas a otros sectores y para la utilización final de estos productos (f i ), se tiene entonces que:
Donde Z ij representa las ventas intermedias o interindustriales del sector i a los demás sectores j (con i=j que son las ventas así mismo). Una forma más precisa y compacta de lo anterior es:
Generalizando y usando notación matricial se tiene:
A partir del sistema [11] se puede obtener los siguiente:
Siendo i un vector columna de cuyos elementos son unos (1). También es conocido como el vector sumatorio. Esto implica que el producto de Zi, brinda como resultado un vector columna cuyos elementos son la suma de las filas de Z. Es el mismo caso para los vectores fila con i'.
En conjunto, con la sumatoria de la matriz de valor agregado y el total de consumo intermedio se tiene:
Las expresiones [12] y [13] indican que la sumatoria de las filas debe ser igual a la sumatoria del número de columnas, i'x' = xi.
El modelo insumo-producto parte de algunos supuestos:
Supone que cada insumo es suministrado por un solo sector de producción (hipótesis de homogeneidad sectorial). Esto implica que se emplea un solo método de producción, por lo cual la posibilidad de sustitución entre los insumos intermedios no es posible, a la vez que cada sector tiene una sola producción primaria; es decir, que no hay producción conjunta.
Con el objetivo de homogeneizar la medición de los agregados, se introduce la hipótesis de invarianza de precios relativos.
Los insumos comprados por cada sector son solamente una función del nivel de producción de ese sector, por lo tanto, la cantidad de insumos varía en la misma proporción que la producción, es decir, que se asume una hipótesis de proporcionalidad estricta: la composición de los productos dentro de cada sector es fija. Esto significa que la función de producción que el modelo de Leontief considera como lineal y, por lo tanto, los coeficientes técnicos se supondrán constantes durante el período de análisis, dado que se supone que el nivel de producción que el sector i vende al sector j, es una proporción constante del nivel de producción del sector.
Se supone que el efecto total de la producción en varios sectores será igual a la sumatoria de los diferentes efectos (hipótesis de aditividad); con esto se excluye toda interdependencia externa de los sectores, excepto la especificada en el propio modelo.
Cuando se utiliza el modelo para realizar proyecciones de precios, debe tenerse en cuenta que se mantiene la relación de precios relativos presente en el año en que se elabora la matriz.
Otra de las cosas importantes en el MIP es el análisis cuantitativo de la estructura de costos unitarios de todos los sectores productivos dada desde la matriz de coeficientes técnicos9. Dicha matriz se obtiene dividiendo todos los elementos de la matriz de transacciones intermedias (z¡j) entre los totales de las columnas correspondientes (xj). La interpretación de cada uno de estos elementos viene siendo: por cada peso del valor producido del sector 2, dicho sector compra α12 centavos de insumos del sector 1. Los coeficientes técnicos se obtienen así: α11=
 =
=
 y m
1=
y m
1=
 va
2 =
va
2 =
 w3=
w3=
 , La matriz de [a
¡j
] se va a llamar la matriz
A
(n x n) y la matriz de [v
hj
] se va a llamar la matriz v (m x n). Para simplificar algo de notación, suponga que se tiene un modelo para tres sectores:
, La matriz de [a
¡j
] se va a llamar la matriz
A
(n x n) y la matriz de [v
hj
] se va a llamar la matriz v (m x n). Para simplificar algo de notación, suponga que se tiene un modelo para tres sectores:
Sea
 una matriz diagonal conformada por los elementos del vector
x,
tal que
una matriz diagonal conformada por los elementos del vector
x,
tal que
partiendo de la definición y existencia de una matriz inversa, se tiene que
 la matriz de coeficientes técnicos puede ser representada por :
la matriz de coeficientes técnicos puede ser representada por :
Sea I una matriz de identidad de (3 x 3), tal que
Matricialmente se tiene que:
donde:
(I-A): es la matriz de Leontief; la suma de cada fila i de la matriz de Leontief [- a¡1- a¡2 + (1- a¡i) +...- ain] indica cuántos centavos del producto i quedan para la demanda final, después de haber satisfecho las demandas intermedias de todos los sectores. La suma de cada columna j de la matriz de Leontief indica cuántos centavos de cada peso del producto j no son atribuibles a los insumos comprados.
En algunos casos resulta conveniente normalizar las columnas de la matriz de Leontief de tal forma que los elementos de la diagonal principal contengan solos unos. Para esto se debe dividir cada columna por elemento (1 - aij). Este tipo de vectores se utiliza en el análisis de actividades que se estudiarán más adelante.
La ecuación [18] tiene la forma de Ax=b, es decir, es la representación de un sistema de ecuaciones lineales. Para resolver este sistema debe existir la inversa de (I-A); si es así, se tiene:
Donde:
(I-A)-1=L: es denominada la matriz inversa de Leontief o matriz de requerimientos totales (directos e indirectos). La ecuación [19] es denominada la solución general del modelo de insumo producto; (I - A) -1 es la matriz inversa de Leontief o matriz de requerimientos totales (directos e indirectos); permite calcular los niveles de producción de todos los sectores de la economía compatibles con los niveles de datos de la demanda final.
Parte de las decisiones que tienen que enfrentar los hacedores de política (policy-makers) está enfocada en dos aspectos esenciales: el primero de ellos es la administración del gasto de forma eficiente y óptima en términos sociales. La segunda está relacionada con la consecución de recursos, esto último en esencia es política tributaria. De aquí se deriva el concepto de la tributación, que se refiere a la manera como deben ser estructurados los impuestos para generar crecimiento y desarrollo económico.
Una parte importante de la literatura se encuentra centrada en calcular multiplicadores desde el punto de vista eco-nométrico (Auerbach & Gorodnichenko, 2012; Cogan et al., 2010; Favero & Giavazzi, 2012; Havranek et al., 2016; Ilzetzki et al., 2013; Mertens & Ravn, 2010; Mountford & Harald, 2009) y otros trabajos han utilizado modelos DSGE (Coenen et al., 2012; Erceg & Lindé, 2014; Giordano et al., 2007; Mitra et al., 2019; Zubairy, 2014) y enfoques mixtos desde los aspectos de la política económica, esto es política fiscal más política monetaria (Davig & Leeper, 2011; Leeper et al., 2013; Mertens & Olea, 2018) y desde la técnicas de estimación (Gechert, 2015; Horn et al., 2017; Mittnik & Semmler, 2012).
En materia de impuestos corporativos existen diferentes trabajos que se enfocan en cuantificar los efectos de los impuestos sobre las empresas (Annabi et al., 2013; Blesse et al., 2019; Brito-Gaona & Iglesias, 2017; Harju & Matikka, 2016; Koga, 2003; Slemrod & Yitzhaki, 2002; Wallis, 2016).
No obstante, hay pocos trabajos que se enfoquen desde la teoría de la tributación óptima y que al mismo tiempo incluyan efectos intersectoriales a partir de modificaciones en los impuestos de otros sectores y que reconozcan que estos efectos son asimétricos a lo largo de la cadena de valor. Por su parte, la literatura relacionada con el modelo de equilibrio general aplicado ha sido ampliamente explorada por Albanesi (2006), Albanesi y Sleet (2006), Atkinson y Stiglitz (1976), Feldstein (1995) y Gruber y Saenz (2002).
La literatura colombiana se encarga de reconocer multiplicadores directores, indirectos e inducidos. Así mismo, se ilustra la potencialidad de la MIP como herramienta de simulación no solo en el ámbito nacional (Hernández, 2012), sino regional (Bonet, 2006; Flórez, 2012; Morrisey, 2014).
El aporte del presente escrito está en reconocer el traspaso de los efectos impositivos teniendo como punto de partida los encadenamientos de insumo-producto, y en brindar una mejor apreciación sobre la forma como los impuestos tienen diferentes efectos en otros sectores. Esto permitirá contribuir a la línea de impuestos, a fin de ofrecer mejores elementos de planificación de la política tributaria.
METODOLOGÍA
El objetivo del presente trabajo consiste en identificar el efecto de los impuestos (directos e indirectos) sobre los sectores de la economía de Colombia. Para poder calcular dichos efectos se utilizó la matriz insumo producto (MIP-61 sectores, simétrica, producto a producto, precios básicos), de la cual se obtuvieron los impuestos netos de producción y la matriz inversa de Ghosh10.
Adicionalmente, con la información proveniente del sistema de información y reporte empresarial SIREM de la Superintendencia de Sociedades (Supersociedades), la cual tiene un registro de más de 355 000 microdatos. Para el período 1995-2015 se calculó un vector de distribución de impuestos directos que se ajustó con la información de la matriz de contabilidad social (SAM, por su sigla en inglés). Las dos fuentes de información relacionadas con los impuestos directos son complementarias, ya que la SAM solo tiene un dato agregado de los impuestos directos (20 669 billones de pesos corrientes para el 2010), mientras que la información del SIREM tiene la desagregación para los 61 sectores que manejan las cuentas nacionales11. Este vector columna es el que se utilizó para las simulaciones basadas con la inversa de Ghosh.
De la matriz de contabilidad social (SAM derivada de la MIP) se obtuvo el resto de los impuestos indirectos (impuestos, excepto IVA, IVA no deducible, impuestos sobre las importaciones). Los cálculos y la manipulación de matrices se realizaron con E-views; no obstante, a efectos de presentación se trasladaron a Excel.
La inversa de Ghosh y la longitud me -dia de propagación (APL)
Ghosh (1958) sostiene que el modelo insumo-producto, en esencia, está en equilibrio, debido a que existen las dos fuerzas de oferta y demanda en el interior de las relaciones. A partir de este principio, Ghosh plantea una nueva matriz de coeficientes (o de distribución), la cual se obtiene de forma horizontal:
cada coeficiente de la matriz de distribución mostrará la proporción, en términos monetarios, que emplea la rama de la fila i-ésima, y que se destina a cada una de las otras ramas o a la demanda final. Con esta nueva forma de plantear el problema se da paso a que los inputs primarios (trabajo o capital empleado en la producción de esa j-ésima rama) sean las nuevas variables exógenas y no la demanda final, como en el caso de la matriz de coeficientes técnicos. De esta forma, los modelos de demanda y oferta permitirían conocer cómo los cambios en ellos afectan a las distintas funciones de producción, ya que ahora se puede trabajar con dos variables exógenas, lo que (...) daría a los resultados (...), mayor flexibilidad. (Soza, 2007, p. 19)
Partiendo de la ecuación (6), se tiene que el sistema estará dado por:
Y la solución será:
Donde B es la matriz de coeficientes de distribución y v es la matriz de inputs primarios o valor agregado. La ecuación 22 es la solución desde el modelo de Ghosh (1960).
Retomando a Soza,
(...) el valor que se obtiene de la suma en filas de la matriz inversa de coeficientes de distribución mostrará el aporte que realiza cada rama para que aumente en una unidad los inputs primarios, por ello, se le conoce como el multiplicador de oferta o de inputs. La suma en columnas de los coeficientes de distribución indica en cuánto cambia la producción si se produce una modificación de una unidad en la oferta (inputs primarios) de cada una de las ramas (...). (2007, p. 20)
Es decir, este modelo de precios permite evaluar de qué manera los cambios en el valor agregado (o de algunos de sus componentes) conducen a cambios en los costos unitarios sectoriales y por lo tanto en los precios de los productos12.
Una vez planteada la estructura analítica básica, se pasa a obtener el impacto de los impuestos directos e indirectos. Sea td un vector fila de coeficientes tributarios de impuestos directos y tid un vector fila de coeficientes tributario de impuestos indirectos, se tienen:
Como el modelo Gosh tiene sentido desde el cambio en los precios, la matriz de efectos totales de los impuestos estará dada por:
Donde diag(td) y diag(tid) son matrices (m x n) cuya diagonal principal son los de coeficientes tributarios directos e indirectos, respectivamente13. Como los impuestos que se utilizan para el ejercicio son sobre los componentes del valor agregado, la ecuación [22] se transforma en:
A través de los multiplicadores tributarios se cuantifica la relación entre los coeficientes y los cambios por unidad de valor agregado.
Con el objetivo de "rastrear" los sectores afectados después de que uno de estos experimenta un incremento de impuestos, se utiliza el APL, el cual permite identificar qué sectores son afectados después del cambio, teniendo en cuenta las interrelaciones sectoriales desde una perspectiva de configuración de clusters. Por lo cual, desde la ecuación [18] se tiene:
La ecuación [19] muestra los cambios en la producción, dado que cambia alguno de los elementos de la matriz de valor agregado. Si los impuestos aumentan en la industria i, los costos de producción aumentarán, y así aumentará el valor de la producción de la industria i; esto es el efecto directo de un aumento en los impuestos. No obstante, como una parte de la producción, 6y,de la industria i, es vendida a la industria j, y como el valor de la producción de la industria i está aumentando, el aumento adicional en los costos de producción se pasa a través de los compradores:
Los efectos de la primea ronda están dados por ∆v'B, los cuales podrían denominarse efectos directos; mientras que los efectos indirectos están dados por ∆v'(B 2 + B 3 +…):
permite definir la matriz de longitud media de propagación (Λ):
Se utilizan ambas metodologías, pues, como menciona Schuschny,
Es importante destacar, que estar en presencia de multiplicadores de gran magnitud, no es lo mismo que grandes impactos multiplicadores, ya que los impactos dependen tanto del valor de los multiplicadores, como de la magnitud de los estímulos externos, que originan el potencial efecto multiplicador. (Schuschny, 2005, p. 35).
ANÁLISIS DE RESULTADOS
La metodología planteada permite, en primera instancia, identificar los sectores más sensibles frente al cambio de los impuestos y posteriormente permite identificar hacia qué otros sectores se propagan los cambios de estos; dado que se tienen 61 sectores desde la clasificación de cuentas nacionales, el análisis de propagación se presenta para los primeros 10 sectores sin perder generalidad para los demás sectores14.
El efecto directo es la mejor manera de identificar qué sectores son afectados ante un cambio en los impuestos. Se debe recordar que los impuestos por analizar son impuestos netos de producción, impuestos excepto IVA, IVA no deducible, impuestos sobre las importaciones e impuesto de renta para las empresas. Para un mejor entendimiento, los multiplicadores se estandarizaron en 1. Así, aquellos que estén por encima de 1, indicarán los sectores que más se afectarán al cambiar alguno de los impuestos.
Los encadenamientos totales hacia adelante y los impuestos directos (impuesto de renta) se presentan en la Figura 1. Allí se indica que hay 21 sectores que son sensibles a los cambios en la estructura del valor agregado. Estos sectores son los que están por encima de la línea roja. Se destaca una alta dispersión en la cantidad de sectores afectados (14) y en la magnitud de estos. Se evidencia que, aunque todas las empresas de los sectores tienen que pagar este impuesto, son influenciadas de distinta manera. Por ejemplo, sectores como la construcción (41 y 42) y alojamiento (45) presentan una sensibilidad más no una pero su efecto es diferente. Una explicación de esto pueden ser las exenciones tributarias que maneja cada sector.
Las figuras 2 y 3 presentan la sensibilidad de los sectores frente al resto de los impuestos; al igual que con el impuesto de renta, estos también se caracterizan por una alta dispersión. En los impuestos netos de producción son 26 sectores los sensibles frente a este rubro; en los impuestos diferentes al IVA son 12, mientras que para el IVA no deducible y los impuestos a las importaciones son 27 y 22 sectores respectivamente.
Los impuestos netos de producción muestran que sectores como la construcción (42), la producción de tabaco (19) y energía eléctrica (38) tienen una alta sensibilidad. Estos sectores de alguna manera tienen una alta proporción de subsidios y/o tratamientos preferencias para poder ejercer operaciones, en ese sentido son coincidentes. De los otros impuestos, excepto IVA, se destacan sectores como comercio (43), servicio de alojamiento (45), los tres de transporte (47-48-49), servicios de alcantarillado; estos sectores en particular revelaron una alta sensibilidad (> 2) frente a los cambios en este componente tributario.
Los impuestos relacionados con IVA no deducible e impuestos sobre importaciones indican una alta sensibilidad en los sectores de equipo de transporte, muebles, otros bienes manufacturados n.c.p., desperdicios y desechos, energía eléctrica, gas domiciliario, agua, trabajos de construcción (construcción y reparación de edificaciones y obras civiles), servicios de arrendamiento de equipo con operario, comercio, servicios de reparación de automotores, de artículos personales y domésticos y servicios de alojamiento, suministro de comidas y bebidas.

Fuente: cálculos del autor.
Figura 2 Sectores sensibles por tipo de impuesto: impuestos netos a la producción e impuestos excepto IVA.

Fuente: cálculos del autor.
Figura 3 Sectores sensibles por tipo de impuestos: IVA no deducible e impuestos sobre importaciones.
La Tabla 1 pone de manifiesto una particularidad: de 61 sectores que se tienen clasificados en la economía, 49 son sensibles a la tributación, cifra importante, ya que constituyen casi el 80 % del aparato productivo. No obstante, estos 49 sectores son transversales a cada impuesto, lo que indica, como se evidencia en la Tabla 1, que no todos son sensibles a los mismos impuestos.
Por ejemplo, los sectores más sensibles por el impuesto de renta solamente son 5, mientras que el potencial tributario para estos sectores es de 21 sectores, diferencia importante sin considerar excepciones tributarias. Si bien es cierto que todas las empresas deben pagar estos impuestos, las exenciones evidencian la alta asimetría tributaria.
Con lo anterior, se ha logrado identificar cuáles sectores son sensibles frente a cambios en los impuestos, directos e indirectos. Ahora se pasa a "rastrear" hacia qué sectores se va cada variación en los impuestos. El ejercicio se realizó para 61 sectores, por lo cual se tendrían 61 efectos de propagación para analizar. Por razones de espacio, solo se muestra el "top 10" de los sectores a los cuales llega el efecto de un cambio en los impuestos en el sector del azúcar (15). La Figura 4 muestra la propagación hacia los otros sectores de un incremento en los impuestos.
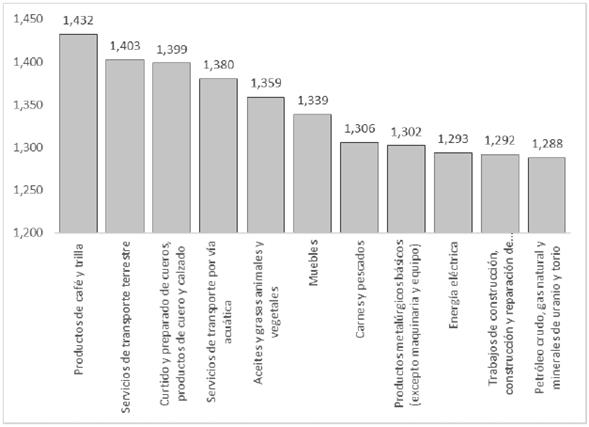
Fuente: cálculos del autor.
Figura 4 Propagación sectorial de un cambio en los impuestos del sector del azúcar (15).
Se puede ver que los cambios se trasladan a productos de café y trilla, seguidos por servicios de transporte terrestre, luego pasan a curtido y preparado de cueros, productos de cuero y calzado, para seguir con servicios de transporte por vía acuática. Sectores como aceites y grasas animales y vegetales, muebles, carnes y pescados, también son afectados, y productos metalúrgicos básicos (excepto maquinaria y equipo), energía eléctrica, trabajos de construcción (construcción y reparación de edificaciones y servicios de arrendamiento de equipo con operario), petróleo crudo, gas natural y minerales de uranio y torio, productos de madera, corcho, paja y materiales trenzables, también son afectados.
Los aspectos asociados a la cadena de valor son un punto de partida para entender este "traspaso"; sin embargo, se debe recordar que estos son sectores, son agrupaciones de empresas, por lo cual un análisis de simulación desde la cadena de valor permitiría validar algunos resultados del presente ejercicio, aunque esto excede el objetivo del escrito.
CONCLUSIONES
El objetivo del presente artículo consistió en identificar la incidencia de los impuestos sobre los sectores de la economía utilizando la MIP como estrategia metodológica. Se encontró que existen sectores altamente sensibles al cambio en los impuestos, pero son sensibles dependiendo del tipo de impuesto.
También se evidencian unos sectores que son comunes a todos los impuestos. Estos tienen fuertes encadenamientos desde la estructura productiva y desde las cadenas de valor que se generan en el interior de cada de uno de ellos. En promedio, más del 35 % de los sectores analizados es afectado, es decir, se evidencia una alta asimetría de la propagación.
Una estructura tributaria óptima implica reconocer dichas asimetrías al momento de gravar un sector. Que existan 49 sectores sensibles a diferentes impuestos es una oportunidad para que haya una reconfiguración en las cargas de los impuestos a favor de otras.
Se destaca que los sectores que tienen mayor propagación en materia tributaria son los de servicios en cuanto a los impuestos netos de producción y los impuestos excepto el IVA; para los impuestos sobre las importaciones la relación se dirige hacia los sectores industriales. Esto se explica por la relación de insumos intermedios importados, así como la alta dependencia importadora que ha presentado el país después de la década del 90.
Para los cuatro tipos de impuestos estudiados se destaca que los efectos directos tienen un mayor alcance en la cantidad de sectores, aunque estos resultados no se reportan. La razón de esto es que el sector con mayor afectación de impuesto es el mismo sector, y no tendría mucho sentido reportar esto; además los MEGC pueden hacer esto, incluso con más precisión. No obstante, esto es lógico desde el punto de vista de los encadenamientos que manejan la estructura de modelación que se utilizó.