INTRODUCCIÓN
La mortalidad infantil (MI) es uno de los indicadores más usados para determinar el nivel de desarrollo de un país (Ordorica & Prud'homme, 2012), debido principalmente a que la mayor proporción de defunciones de menores ocurre en países subdesarrollados. De acuerdo con la Organización Mundial de la Salud (OMS, 2020), en 2019 en el mundo murieron más de 5 millones de niños menores de cinco años, de los cuales, 1.5 millones eran menores de un año. Esta cifra en México alcanzó las 19 336 defunciones de menores de un año en 2020.
En México, desde hace más de treinta años se ha observado un descenso sostenido de la MI, que puede ser explicado a partir de la teoría de la transición epidemiológica y sus implicaciones en relación con los cambios en la sobrevivencia infantil (Aguirre & Vela, 2012), en especial, los asociados a la prevalencia de enfermedades infectocontagiosas, que afectan principalmente a niños menores de un año (CEPAL-CELADE, 2005; Arriagada, 2004). La tasa de mortalidad infantil (TMI), entendida como las defunciones de menores de un año por cada mil nacimientos, contabilizadas a lo largo de un año calendario, se ha reducido significativamente. En el caso de México, se pasó de 120 defunciones de niños menores de un año por cada mil nacimientos, en 1950, a 16.8 por mil en 2005 (Ordorica & Prud'homme, 2012) y a 12.8 defunciones por cada mil nacimientos para 2020 (CONAPO, 2020a). Esta reducción puede ser atribuida tanto a esfuerzos institucionales (Secretaría de Salud-Gobierno de México, 2022) como a importantes mejoras en las condiciones generales de vida de la población, especialmente en materia de acceso a la salud. Sin embargo, se debe enfatizar la presencia de importantes rezagos, derivados de la presencia de un considerable número de defunciones de menores debidas a causas infectocontagiosas.
El objetivo de este trabajo es analizar las diferencias en los niveles de MI entre los municipios de México al año 2020, así como evidenciar la existencia de patrones de asociación espacial generados por la formación de conglomerados de municipios con altos/bajos niveles de mortalidad infantil. El marco teórico utilizado para explicar los niveles observados de mortalidad infantil entre municipios se basa en el esquema propuesto por Mosley y Chen (1984), mientras que el análisis de los patrones de distribución espacial se apoyan en el uso y aplicación de modelos espaciales econométricos.
Los modelos econométricos permiten establecer relaciones entre una variable y su localización espacial, así como identificar interacciones espaciales endógenas, exógenas y entre términos de error. Por lo anterior, la dependencia espacial puede presentarse entre la variable dependiente, las variables independientes y el término de error. Cuando el modelo capta la dependencia espacial en la variable dependiente, se denomina de rezago espacial, mientras que, si es captada por el término de error, se tiene un modelo de error espacial.
La MI puede ser considerada el resultado de un proceso en el que interviene un conjunto muy amplio de determinantes próximos y contextuales (Mosley & Chen, 1984). Los determinantes actúan de forma diferencial en cuanto al contexto socioeconómico y el entorno geográfico, que es influenciado por la presencia de relaciones de interacción establecidas de forma espacial. El marco propuesto por Mosley y Chen introduce variables intermedias indirectas o socioeconómicas, que tienen por objeto mejorar la comprensión de la relación salud-enfermedad. Dada la naturaleza multicausal de la relación salud-enfermedad, esta suele agruparse en tres niveles: individual, familiar y macrosocial (Morelos, 2001).
El uso de modelos econométricos de regresión espacial permite evaluar el efecto de los niveles de escolarización de las mujeres, el acceso a servicio de agua potable, el nivel de acceso a servicios de salud y la marginación sobre la tasa de mortalidad infantil presente en los municipios de México en el año 2020. Es importante señalar que el índice de marginación es utilizado como un indicador que pretende capturar las condiciones de desigualdad social presentes en los municipios, es decir, como un factor que busca explicar las diferencias de la mortalidad infantil derivadas del nivel de aislamiento social y geográfico presente en los diferentes municipios de México. De modo que plantear la hipótesis de que la desigualdad en la distribución espacial del acceso a servicios de salud, agua potable y niveles de escolaridad femenina desempeña un papel fundamental para explicar las diferencias observadas de mortalidad infantil entre municipios en México. Es decir, que mejoras significativas en dichos factores deberían implicar una importante reducción de los niveles de mortalidad infantil.
ANTECEDENTES
Los trabajos de investigación relacionados con la mortalidad infantil se han incrementado debido tanto a la relevancia del indicador -el cual, recordemos, también es utilizado como un indicador de desarrollo- (Longhi, 2013; Hernández & Narro Robles, 2019; Schkolnik & Chachkiel, 1998) como a su uso en contextos como los Objetivos del Desarrollo Sostenible (ODS). El ODS 3.2.1 tiene como fin promover la salud y el bienestar de los niños, y poner fin a las muertes evitables al 2030 (ONU, 2022). Para el logro de dicho objetivo se plantea la equidad en el acceso, la cobertura y calidad de los servicios de salud para todos los niños (OMS, 2020).
La MI es un indicador en el que la relación entre salud, enfermedad y muerte se presenta como resultado de la interacción entre los contextos económico, biológico y social (Longhi, 2013). Según Mosley y Chen (1984), los determinantes sociales y económicos operan a través de un conjunto de mecanismos biológicos que afectan los niveles de mortalidad. Estos se denominan determinantes próximos y estructurales. El primero de los determinantes (próximos) vincula a la MI con aspectos como edad materna, número de hijos, intervalo intergenésico, peso al nacer; mientras que el segundo de los determinantes (estructural o contextual) comprende aspectos relacionados con el medio ambiente, la contaminación, la estructura socioeconómica, entre otros.
Dentro del grupo de determinantes próximos se destacan trabajos de corte espaciotemporal, en los que se vincula la mortalidad infantil y enfermedades (Dipierri et al., 2015) o problemas de desnutrición (Longhi & Del Castillo, 2017) como causantes de las muertes en niños menores de un año. En México y América Latina, Arriaga (1996), Aguirre y Vela (2012) y Yasmin (2002) analizan el efecto de los determinantes próximos sobre el comportamiento de la tasa de mortalidad infantil. Concluyen, en general, que la responsabilidad de las muertes se debe a comportamientos y actitudes personales, muchos de ellos de índole cultural, que retardan u obstaculizan la actuación de los sistemas de salud.
Por otro lado, los estudios del segundo grupo, pertenecientes a las variables estructurales de Mosley y Chen (1984), analizan factores como pobreza, ingreso, nivel de instrucción de la madre, condiciones de la vivienda, acceso a los servicios de salud, procesos migratorios y las crisis y sus relaciones con la salud (Longhi, 2013).
Algunos estudios de este grupo subrayan la prevalencia de la MI en entornos rurales (CEPAL-CELADE, 2005; Duarte-Gómez, et al., 2015) y con niveles bajos de escolaridad de la madre (CEPAL-CELADE, 2005), en los que la tendencia resulta más notoria al triplicar la TMI para madres sin instrucción comparadas con madres que cuentan con niveles superiores a la instrucción secundaria.
En los estudios realizados desde la perspectiva espacial en la última década, se establece la correlación entre mortalidad infantil y el nivel socioeconómico de su población a partir de variables como la escolaridad, el ingreso familiar, las viviendas con hacinamiento o construidas con materiales precarios, acceso a un automóvil y a servicios de salud (Álvarez et al., 2009). En Chamizo y Ammazzini (2014) se establecen correlaciones lineales entre la MI e indicadores como el índice de desarrollo humano y un indicador sintético de calidad ambiental a nivel comunitario, mientras que en Duarte-Gómez et al. (2015) se consideró el acceso a instituciones de salud. También ha recibido especial atención el análisis de la relación entre MI y pobreza. En Longhi (2013) y Duarte-Gómez et al. (2015) se destaca el limitado acceso a redes de agua potable y saneamiento, las condiciones de acceso a servicios de salud debido a falta de carreteras, transporte público y medios de comunicación, las limitaciones económicas para el pago de transporte debido a las distancias que deben recorrer y la falta de autonomía de las mujeres en la toma de decisiones sobre la búsqueda de atención, que también se explican por el contexto de pobreza, como en Salcedo y Ortiz-Rico (2018) y Sánchez et al. (2018), donde se prueba la existencia de dependencia espacial con las desigualdades sociales que hay en el ámbito municipal.
En materia de medición de desigualdades de acceso a servicios de salud general y maternoinfantil es evidente la presencia de importantes limitaciones, entre las que se destacan problemas de calidad y disponibilidad de servicios de salud, en especial para las poblaciones en peor situación económica (Almeida-Filho, 1999); lo que implica que el acceso a los servicios de salud tienen un papel fundamental para reducir los factores de riesgo asociados a la incidencia de defunciones infantiles. Algunos trabajos coinciden en que la mayor limitante para la estimación y el análisis de la MI depende tanto del acceso a la información como de la calidad de los registros de mortalidad infantil (Ruiz-Santacruz & Duran-Gil, 2014), debido a que su baja calidad no permite apreciar con claridad el nivel y la tendencia del fenómeno.
La incidencia del índice de marginación sobre el comportamiento de la mortalidad de menores de un año se relaciona a través de factores asociados al acceso a servicios de salud, características de las viviendas, hacinamiento, estatus socioeconómico del jefe de hogar y alfabetización femenina. La relación entre los niveles de mortalidad infantil y las condiciones de vida, en términos de un conjunto de factores socioeconómicos que imponen fuertes restricciones al acceso y calidad de servicios en materia de salud, están ligados a las condiciones de pobreza estructural que configuran, espacial y temporalmente, los mecanismos a través de los cuales se establecen los determinantes de la mortalidad infantil en países latinoamericanos (Spinelli et al., 2000).
FUENTES DE INFORMACIÓN Y DATOS
La información utilizada para cuantificar los niveles de mortalidad infantil en el ámbito municipal proviene del registro de defunciones elaborado por la Dirección General de Información en Salud, dependiente de la Secretaría de Salud de México, y corresponde a las defunciones registradas durante el año 2020, mientras que la información requerida para evaluar el nivel de acceso a los servicios públicos como agua potable, servicios de salud y educación fue obtenida de los registros del Censo General de Población y Vivienda 2020 (INEGI, 2020a). Finalmente, la información sobre los niveles de marginación municipales se obtuvo de las estimaciones sobre marginación realizadas en el orden municipal por el Consejo Nacional de Población, las que se encuentran disponibles en su página web (CONAPO, 2020b). Es importante señalar que la información proveniente de las tres fuentes citadas se integró a través de registros municipales utilizando la clave geográfica asignada por el INEGI.
A pesar de la importancia relativa de las defunciones de menores de edad, no existe en México un adecuado sistema de recolección de estadísticas vitales que permita cuantificar de forma confiable las defunciones y nacimientos de menores de un año. Las deficiencias en el registro de hechos vitales de menores de edad están sujetas a la presencia de inconsistencias provocadas por la falta de declaración, el subregistro y sesgos provocados por la preferencia de dígitos tanto del registro de nacimientos como de defunciones. Debido a la mala calidad detectada en los datos provenientes del registro de defunciones (problemas asociados al subregistro, mala declaración y preferencia de dígitos). Se utilizó el método de Trussel (1975) para estimar de manera indirecta las tasas de mortalidad infantil. Los determinantes utilizados para construir el modelo que explique el comportamiento espacial de la MI para el desarrollo del presente trabajo, comprenden el acceso a servicios de salud, el acceso a agua potable dentro de las viviendas y la escolaridad femenina, medida a partir de los años promedio de escolaridad, así como el índice de marginación. Los determinantes permitirán evaluar el comportamiento de las tasas de MI municipal con base en la aplicación de una serie de modelos espaciales econométricos.
METODOLOGÍA
Estimación de tasas de mortalidad infantil
La estimación de la tasa de mortalidad infantil (TMI) para las 32 entidades federativas y los 2469 municipios, que conformaron la división política de México para el año 2020, se realizó a través de la aplicación del método de Trussel (1975) con información sobre la proporción de hijos nacidos vivos e hijos fallecidos por edad de la madre. El método permite asignar una fecha a cada estimación, lo que hace posible reconstruir la tendencia temporal de la evolución de las tasas de mortalidad infantil para estados y municipios, de forma que puedan suavizarse las anomalías detectadas en el comportamiento de las tasas a lo largo del tiempo (Feeney, 1980).
Las estimaciones de las tasas de mortalidad infantil para México en el año 2020 arrojaron un total de 12.2 fallecimientos por cada mil nacidos vivos, mientras que la tasa de mortalidad infantil estimada por CONAPO (2020c) fue de 12.8 para México en el mismo año, lo que supone la ocurrencia de alrededor de 21 000 decesos infantiles a lo largo del año, cifra que contrasta con las defunciones de menores de un año reportada de 19 336 defunciones de menores, según lo reportado en las estadísticas vitales al año 2020 (INEGI, 2020b). Si consideramos que nacieron 1 629 211 menores durante el 2020, el subregistro resulta ser del orden del 12 % a nivel nacional, mientras que para las entidades federativas y los municipios se observan importantes variaciones entre el registro de defunciones y las tasas reportadas.
El comportamiento en el ámbito municipal de las tasas de mortalidad infantil se caracterizó por presentar importantes diferencias entre regiones de México, tal y como puede verse en el Mapa 1. La TMI más baja se registró en el municipio de Pueblo Nuevo, Guanajuato, la cual ascendió a 3.5 defunciones por cada mil nacimientos, en tanto que la tasa más alta se presentó en el municipio de Santa Isabel, Chihuahua, con 51.9 muertes infantiles. En términos generales, las entidades donde se registraron las mayores tasas de mortalidad infantil fueron Oaxaca, Puebla, Sonora y Coahuila con tasas superiores a 48 defunciones de menores de un año por cada mil nacidos vivos, en contraste con la Ciudad de México o Monterrey, donde se registró una media de 12.5 y 11.6 defunciones de menores por cada mil nacimientos respectivamente.
ANÁLISIS EXPLORATORIO DE DATOS ESPACIALES
El trabajo estadístico comienza con un análisis exploratorio de datos espaciales (AEDE). El AEDE tiene como propósito fundamental identificar patrones de agrupamiento espacial, descubrir y/o detectar valores espaciales aberrantes y estructuras, a través de la aplicación de una serie de estadísticos, diagramas, gráficas y mapas (Chasco, 2003), lo que permite comenzar a visualizar la distribución espacial de los datos. El acercamiento utilizado para la detección de patrones de asociación espacial se basa en el postulado establecido por Tobler (1970, p. 236) en su primera ley, que dice: "todo está relacionado con todo, pero las cosas cercanas están más relacionadas que las cosas distantes". La ley de Tobler es el principal antecedente para definir la autocorrelación espacial como una medida de asociación entre unidades espaciales o regiones, con base en los valores que toma un atributo "y" presente en cada unidad espacial.
El proceso de análisis exploratorio de datos inicia con la aplicación de pruebas de autocorrelación espacial global (I de Moran) a la variable endógena y a las variables exógenas (explicativas) presentadas en la sección anterior. El objetivo es obtener evidencia de la existencia de correlaciones espaciales, para lo que se utiliza una matriz de pesos espaciales calculada a partir del criterio del vecino más cercano, que considera la distancia entre municipios establecida a partir del criterio de vecindad. Así, el índice de Moran global estima la auto-correlación con base en la ubicación del municipio y los valores del atributo "y" para todos los municipios de forma simultánea; es decir, dado un conjunto de municipios y un atributo, el índice de Moran global evalúa la existencia de patrones de agrupación, de dispersión o la ausencia de patrones (i.e., existe una distribución aleatoria).
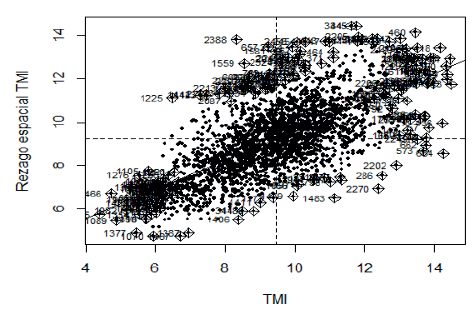
Fuente: elaboración propia con estimaciones realizadas en R.
Figura 1 Diagrama de dispersión de Moran para la tasa de mortalidad infantil
El índice de Moran de autocorrelación espacial global devuelve valores entre -1 y +1 (valores cercanos a +1 indica la presencia de patrones de asociación espacial positiva, mientras que valores cercanos a -1 indican la presencia de patrones de dispersión. Valores cercanos a cero indican la ausencia de correlación). Los valores de índice de
Moran permiten definir conglomerados espaciales, los cuales se clasifican en cinco categorías (Ord & Getis, 1995): (1) low-low: se denomina zona fría, conformada por unidades espaciales con valor inferior al promedio del atributo de interés, rodeadas de unidades vecinas con valores similares; (2) low-high: unidades espaciales con valor debajo del promedio para la variable de interés, rodeadas por unidades con valores por encima del promedio; (3) high-low: unidades espaciales con valores superiores al promedio para la variable de interés, rodeadas por unidades con valores por debajo del promedio; (4) high-high: denominada zona caliente, conformada por agrupamiento de unidades espaciales con valor superior al promedio, rodeadas por unidades con valores por arriba de la media, respecto a la variable de interés; y (5) no significativo: el conjunto de unidades espaciales donde la variable de interés no se correlaciona significativamente con los valores que presentan sus vecinos.
Adicionalmente, el índice de Moran permite comprobar la hipótesis sobre la existencia de patrones de agrupa-miento espaciales (Odland, 1988). En el Cuadro 1 se presentan los resultados de las estimaciones del índice de Moran, que muestran la existencia de autocorre-lación espacial global. Los valores del índice de Moran resultaron positivos en todos los casos, lo que indica que existe una asociación espacial directa entre la variable y el espacio, tal y como puede confirmarse en la Figura 1.
Cuadro 1 Prueba de autocorrelación espacial de Moran global
| Moran I | Expectation | Variance | z.value | P(z) | |
|---|---|---|---|---|---|
| log_tmi | 0.199 | 0.00 | 0.001 | 8.05 | 0 |
| ass | 0.529 | 0.00 | 0.001 | 21.38 | 0 |
| sagua | 0.226 | 0.00 | 0.001 | 9.15 | 0 |
| escfem | 0.551 | 0.00 | 0.001 | 22.26 | 0 |
| log_pob | 0.673 | 0.00 | 0.001 | 27.19 | 0 |
Fuente: elaboración propia a partir de estimaciones realizadas con R
Las variables de carencia de acceso a servicios de salud, años de escolaridad femenina y tamaño de población presentaron un elevado índice de auto-correlación espacial, de acuerdo con el valor registrado en el índice de Moran global (ver Cuadro 1), mientras que las variables de acceso a agua potable y la tasa de mortalidad infantil mostraron niveles de autocorrelación relativamente bajos; sin embargo, los niveles de autocorrelación espacial resultaron ser estadísticamente significativos en todos los casos (i.e., alcanzaron un p-value menor a 0.05, ver Cuadro 1). Lo que permite asumir la presencia de relaciones espaciales que pueden modificar los niveles de mortalidad infantil para el espacio geográfico en el año analizado.
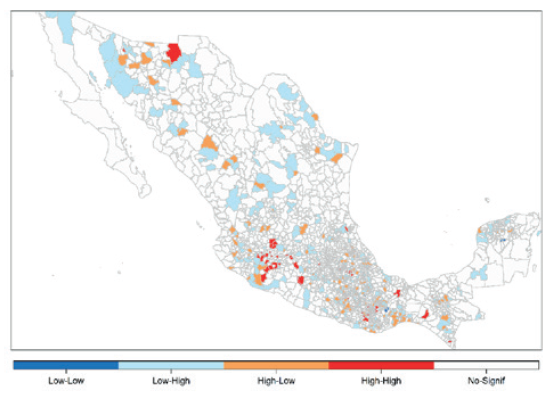
En el Mapa 1 se presenta la distribución espacial de las tasas de mortalidad infantil municipales, lo que permite realizar conjeturas sobre el comportamiento de las tasas. El Mapa 2 presenta los niveles de asociación espacial global en las cinco categorías definidas por Ord y Getis (1995) para la tasa de mortalidad infantil. En términos generales, se observan algunos conglomerados con altos niveles de mortalidad infantil concentrados en el norte de México en los estados de Sonora y Chihuahua, en el sur de Oaxaca, Chiapas y en Yucatán, tal y como puede verse en el Mapa 2. Del mismo modo, pueden observarse algunos conglomerados de media y baja concentración de mortalidad infantil distribuidos a lo largo de México. En cualquier caso, es importante señalar que en la mayor parte de los municipios del país no se observó la presencia de correlación espacial para la mortalidad infantil.
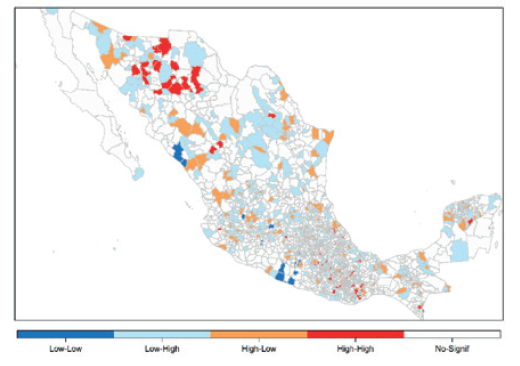
Fuente: elaboración propia a partir de estimaciones realizadas con R.
Mapa 2 Moran de la tasa de mortalidad infantil. Distribución espacial de las tasas de mortalidad infantil municipales mediante el test de Moran.
Acceso a servicios de salud
El Mapa 3 muestra los conglomerados espaciales formados por el índice de Moran global para la variable de carencia de acceso a servicios de salud a nivel municipal. En ella se observan algunos conglomerados con correlaciones espaciales altas-altas, altas-bajas, bajas-altas y bajas-bajas, los cuales se encuentran distribuidos a lo largo y a lo ancho de todo el territorio nacional y presentan un patrón casi aleatorio. Sin embargo, es importante señalar que la variable revela un importante nivel de correlación espacial, a pesar de que en una importante proporción de municipios no se observa (ver Mapa 3). En general, la falta de correlación espacial indica que no existe un patrón de distribución espacial de concentración o dispersión de acceso a servicios de salud, por lo que puede concluirse que la población tiene un nivel de acceso homogéneo a los servicios de salud a nivel nacional, a excepción de los municipios marcados en tonos rojos o azules en el Mapa 3.
Carencia de acceso a agua potable
El concepto de vivienda abarca, además de la disponibilidad de espacios acondicionados para realizar las actividades cotidianas, el acceso a servicios de saneamiento y agua potable, lo que la Organización de Naciones Unidas (ONU, 1996) denomina vivienda adecuada. El acceso a agua (especialmente agua potable) dentro de la vivienda forma parte de los servicios básicos y permite estratificar a la población desde una dimensión social; el hecho de disponer de agua potable mejora significativamente las oportunidades de sobrevivencia de los niños, en particular de los menores de un año. Se ha demostrado la existencia de una asociación inversa entre las condiciones socioeconómicas y las tasas de mortalidad infantil (Morelos, 2001).

Fuente: elaboración propia a partir de estimaciones realizadas con R.
Mapa 4 Índice de Moran local de carencia de acceso a agua en viviendas particulares habitadas en municipios de México 2020
La autocorrelación espacial de la carencia de acceso al agua en las viviendas puede asociarse directamente con mayores tasas de mortalidad infantil, básicamente con una mayor incidencia de diarreas en menores de edad. La Mapa 4 muestra el índice de Moran global de la variable de carencia de acceso a agua; en ella se aprecian cinco conglomerados, sin embargo, en la mayor parte del territorio se observa que la variable no presenta correlación espacial, salvo en los municipios dibujados en color rojo y azul.
Escolaridad femenina (ESCFEM)
El indicador relativo a los años promedio de educación de las mujeres se relaciona con los niveles de mortalidad infantil al demostrar una relación directa entre ambas variables. Durante el primer año de vida sobrevivirán más aquellos menores cuyas madres cuenten al menos con la educación básica sin importar la calidad de la educación recibida. El incremento en el nivel educativo es un factor que favorece de manera directa la sobrevivencia de los menores de un año, principalmente cuando se trata de los modos de transmisión de las enfermedades y la forma y frecuencia de algunas causas de muerte (Morelos, 2001). En otras palabras, la educación permite a las madres tomar mejores decisiones respecto de la importancia de determinados síntomas, lo que eventualmente puede mejorar las probabilidades de sobrevivencia de sus hijos.

Fuente: elaboración propia a partir de estimaciones realizadas con R.
Mapa 5 Moran de escolaridad femenina. Índice de Moran local de escolaridad femenina en municipios de México 2020
En México, en el año 2020 la escolaridad promedio de las mujeres alcanzó los 9.6 años; no obstante, se observan grandes diferencias entre municipios, donde las menores tasas de escolarización se corresponden con municipios de baja densidad poblacional, elevados porcentajes de población indígena o localizados en zonas de difícil acceso, lo que contrasta con los municipios donde existen los mayores niveles de escolarización, los cuales se encuentran generalmente localizados en zonas urbanas, de fácil acceso y con población mayoritariamente mestiza. Empero, la variable indica elevados niveles de autocorrelación espacial solo en un pequeño número de municipios marcados en tonos rojos y azules de la Mapa 6, contrario a lo observado en los municipios restantes que no presentan evidencia de autocorrelación; no obstante, en términos globales la variable presenta autocorrelación espacial positiva (ver Cuadro 1).
Población municipal
El tamaño de la población es un factor fundamental para entender la disponibilidad de infraestructuras, servicios públicos y la calidad de vida de los habitantes de un municipio. El tamaño de la población afecta directamente la relación oferta-demanda de infraestructura básica, como carreteras, transporte público, agua potable y energía eléctrica. Variables fuertemente correlacionadas con la calidad de vida que inciden directamente en los niveles de sobrevivencia de la población. Una mayor población implica una mayor demanda de servicios como escuelas, hospitales, parques, para satisfacer sus necesidades. Por lo que un municipio con más habitantes debe contar con más y mejor infraestructura y servicios que municipios con pocos habitantes.
En términos generales, los municipios con poblaciones pequeñas están rodeados de municipios con poca población y viceversa, por lo que es de esperarse que la variable presente elevados niveles de autocorrelación espacial. La autocorrelación espacial de la variable tamaño de la población por municipio, presentada en función del logaritmo natural del total de habitantes por municipio, puede verse en la Mapa 6.
En la Mapa 6 se observa un conglomerado de municipios con baja-baja autocorrelación espacial. Esto implica que se trata de un conjunto de municipios con poca población rodeados a su vez por municipios con poca población. El conglomerado se encuentra localizado en el norte de México, en el estado de Sonora, sin embargo, en el mapa pueden verse también otros dos conglomerados de las mismas características localizados en los estados de Guerrero y Chiapas, al tiempo que se observan una serie de municipios dispersos por todo el territorio mexicano, que presentan diferentes niveles de autocorrelación. No obstante, como el resto de las variables analizadas, la mayor parte de los municipios no evidencian autocorrela-ción espacial (ver Mapa 6).
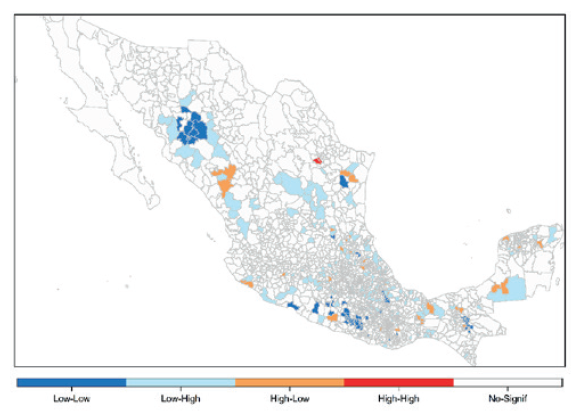
Fuente: elaboración propia a partir de estimaciones realizadas con R.
Mapa 6 Moran del tamaño de municipio. Autocorrelación espacial de la variable tamaño de la población por municipio
Distintos modelos econométricos se ajustaron con la finalidad de modelar el comportamiento de la mortalidad infantil municipal en relación con las covariables analizadas. Las covariables fueron incluidas en los modelos econométricos de mortalidad infantil, debido a su importancia teórica y conceptual para explicar el comportamiento de los niveles de mortalidad infantil, así como su distribución espacial.
MODELOS DE REGRESIÓN ESPACIAL
El modelado espacial de datos busca establecer relaciones entre las observaciones de una variable y cada una de sus localizaciones espaciales. De acuerdo con Elhorst (2014), los modelos de regresión espacial permiten identificar tres tipos de interacción espacial: (1) interacción endógena entre la variable dependiente (Wy) y las unidades espaciales; (2) interacción exógena entre la variable dependiente y las variables independientes (Wx); (3) interacción entre los términos de error (Wu). Además de las interacciones del modelo espacial, se suele incluir una variable adicional u que captura la heterogeneidad espacial y el efecto de las variables omitidas para cada unidad espacial (Ripley, 1981). Los métodos de regresión espacial se fundamentan en la inclusión de criterios basados en la cercanía, como la distancia que se usa para estructurar la dependencia espacial, a través de la matriz W de pesos espaciales que se emplea en la especificación y definición de tales criterios (Getis & Ord, 1992).
El modelo de regresión lineal simple se utiliza como modelo base de comparación respecto de los modelos de regresión espacial, debido a que el modelo de regresión lineal simple permite capturar la relación funcional entre la variable dependiente y las explicativas y estudiar cuáles son las causas de la variación de la primera. Sin embargo, cuando se analizan datos espaciales, el supuesto de independencia entre las observaciones genera inconsistencias derivadas de la dependencia espacial. Esta dependencia espacial puede presentarse tanto en la variable dependiente como en las variables explicativas y en los errores.
Cuando la dependencia espacial capturada por el modelo se encuentra en los residuos, este se denomina modelo de error espacial, mientras que, si la dependencia espacial capturada por el modelo se halla en las variables explicativas, el modelo se llama de regresión cruzada. Por otro lado, cuando la dependencia capturada por el modelo se encuentra en la variable dependiente, el modelo se denomina de rezago espacial. En general, estos modelos permiten que las observaciones de la variable dependiente dependan del comportamiento de observaciones cercanas. El modelo de regresión espacial se refiere al modelo con tantos parámetros como observaciones, lo que permite un buen ajuste de los datos. Su fórmula está dada por:
Wy denota los efectos de interacción endógena de las unidades espaciales, WX denota la matriz de efectos de interacción exógena espacial, Wu captura los efectos de interacción de los términos de error con las unidades espaciales, p representa el coeficiente espacial autorregresivo, que determina el nivel de relación autorregresiva espacial entre yit y Wyit. Θ y ß son los vectores de parámetros por estimar y W es la matriz de pesos espaciales.
Wy indica los efectos de interacción endógena de las unidades espaciales, WX expresa la matriz de efectos de interacción exógena espacial, Wu captura los efectos de interacción de los términos de error con las unidades espaciales, p representa el coeficiente espacial autorregresivo, que determina el nivel de relación autorregresiva espacial entre yit y Wyit. Θ y ß son los vectores de parámetros por estimar y W es la matriz de pesos espaciales.
A partir del modelo saturado de regresión espacial (1), se derivan distintos modelos: el modelo espacial autorregresivo (SAR) cuando Θ =0 y λ=0; el modelo de errores espaciales (SEM) cuando p=0 y 9=0; el modelo espacial Durbin (SDM) cuando ) λ=0, que combina una variable dependiente autorregresiva y covariables dependientes autorregresivas y covariables con retardo espacial (Wy y WX); el modelo de error espacial de Durbin (SDEM), que comprende el término de error espacial combinado con las covariables espacialmente desfasadas (Wu y WX), y el modelo espacial autorregresivoo combinado (SAC) que incluye los términos de autocorrelación de la variable dependiente y de error (Wy y Wu).
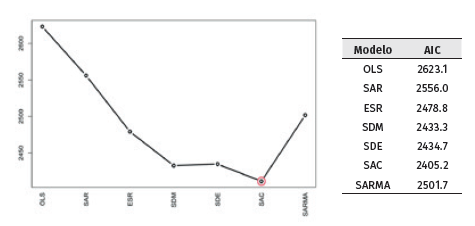
Fuente: elaboración propia a partir de estimaciones realizadas con R.
Gráfico 1 Criterio AIC de selección de modelo
Es recomendable utilizar un modelo de regresión espacial cuando se tiene evidencia de heterogeneidad y/o dependencia espacial, debido a que el modelo de regresión simple no las considera. Cuando los supuestos de independencia entre unidades transversales se violan, se producen estimaciones sesgadas e inconsistentes, lo que implica que las observaciones, tomadas de unidades cercanas, tenderán a mostrar patrones de comportamiento similares.
La retroalimentación simultánea es una característica de los modelos de regresión espacial, cuando se dan intercambios de dependencia entre regiones y dentro de la unidad de análisis. Estas interacciones se generan por la influencia de otra variable y esta, a su vez, provoca cambios en las unidades vecinas, que regresan a la unidad original. La heterogeneidad espacial es recibida por la variable dependiente mediante la influencia de atributos no observados de influencia entre unidades vecinas, como factores económicos, culturales o sociales (Anselin, 1988).
Para construir un modelo espacial para la mortalidad infantil municipal, se consideraron las variables: porcentaje de población sin acceso a servicios de salud, porcentaje de viviendas sin acceso a agua, años promedio de escolaridad femenina y el logaritmo de la población total municipal. Al mismo tiempo, se ajustaron los modelos de regresión lineal simple (OLS), un modelo espacial autorregresivo (SAR), un modelo espacial autorregresivo con error (ESR), un modelo Durbin (SDM), un modelo Durbin con error (SDE), un modelo SAC y un modelo espacial auto-rregresivo de media móvil (SARMA) (ver Gráfico 1).
Una vez estimados los modelos, se aplicó un criterio de selección para elegir el modelo que mejor ajustase los datos de mortalidad infantil. La elección del modelo más adecuado se realiza a partir de la prueba de especificación, lo que representa un paso importante para el desarrollo del modelo econométrico espacial. Para ello se utilizó el criterio de información de Akaike (AIC) que proporciona una medida de calidad de ajuste del modelo. Dada una colección de modelos, el criterio AIC estima la calidad de ajuste de cada modelo y proporciona un medio de selección a partir del valor de la función de máxima verosimilitud evaluada por cada modelo y el número de parámetros estimados, de forma que se selecciona el modelo que alcance el menor valor reportado por el criterio AIC. Los resultados alcanzados al aplicar la prueba AIC a los diferentes modelos se presentan en el Gráfico 1. El modelo que mejor ajusta los datos de mortalidad infantil para los municipios de México en el año 2020, según el criterio AIC, fue el modelo SAC (ver Gráfico 1).
Cuadro 2 Prueba de multiplicadores de Lagrange
| Prueba | parámetro | z-score | p.value |
|---|---|---|---|
| LMerr | 135.51 | 8.12 | 0 |
| LMlag | 71.92 | 6.32 | 0 |
| RLMerr | 95.44 | 9.55 | 0 |
| RLMlag | 31.84 | 5.52 | 0 |
Fuente: elaboración propia a partir de estimaciones realizadas con R.
Otra forma de comparar el ajuste entre modelos de error espacial y modelos de rezago espacial es a través de la prueba de multiplicadores de Lagrange, la cual se basa en un contraste de verosimilitudes. La prueba compara el cambio relativo de la primera derivada de la función de verosimilitud en torno de la verosimilitud máxima, evaluando los parámetros autorregresivos p o λ. La prueba de multiplicadores de Lagrange establece las hipótesis p = 0 o λ = 0 (por lo que el modelo de retardo como el de error se simplifican en un modelo lineal simple), a medida que el valor de los parámetros cambia, también lo hace la función de verosimilitud; de modo que la prueba selecciona, entre un modelo de rezago o un modelo de error, el modelo que alcanza el mayor valor (en particular del estadístico robusto RLM). Los resultados de la aplicación de la prueba de multiplicadores de Lagrange se presentan en el Cuadro 2, donde puede verse la evidencia en favor de los modelos de error espacial.
Cuadro 3 Anova para modelos de regresión espacial SAC-SDM
| € | Model | df | AIC | logLik | Test | L.Ratio | p.value |
|---|---|---|---|---|---|---|---|
| mod.sac | 1 | 8 | 2405.16 | -1194.58 | - | - | |
| mod.sdm | 2 | 11 | 2433.28 | -1205.64 | 1 vs 2 | 22.13 | 0 |
Fuente: elaboración propia a partir de estimaciones realizadas con R.
Adicionalmente, se aplicó una prueba de log-verosimilitud a los modelos de rezago espacial que presentaron los dos valores menores de la prueba AIC, es decir, los modelos SAC y SDM (ver Gráfico 1). Formalmente, la prueba anova de cociente de verosimilitudes (LR) presenta evidencia en favor del modelo alternativo SAC, lo que permite rechazar el modelo SDM (ver Cuadro 3), y demuestra que es consistente con lo aportado por el estadístico AIC.
RESULTADOS
Los efectos de las covariables analizadas permiten mediar el nivel de exposición de los niños al riesgo de contraer enfermedades e influyen sobre la disponibilidad y el acceso a la utilización de recursos preventivos y curativos de atención a la salud, lo que eventualmente mejora los niveles de sobrevivencia de los menores en su municipio y en municipios vecinos. Tomando como base las relaciones teóricas señaladas en los apartados anteriores, se ajustó un primer modelo de regresión lineal simple (OLS). El resultado de las estimaciones se muestra en la Cuadro 2. Es importante resaltar que los coeficientes estimados manifiestan problemas de heterocedasticidad y autocorrelación, por lo que este modelo se presenta únicamente con fines comparativos.
Como se observa en el Gráfico 1, se estimaron siete modelos de regresión, seis modelos de regresión espacial y un modelo de regresión lineal simple. Los resultados de los parámetros evaluados para todos los modelos pueden verse en la Cuadro 2. El Cuadro 3 expone tanto las estimaciones de los parámetros como las pruebas de hipótesis correspondientes al modelo SAC, que resultó ser el modelo seleccionado por el criterio AIC para ajustar los datos de mortalidad infantil de los municipios de México en el año 2020.
Cuadro 4 Modelos de regresión espacial
| OLS | SAR | ESR | SDM | SDE | SAC | SARMA | |
|---|---|---|---|---|---|---|---|
| (Intercept) | 2.534 (45.63) | 2.21 (33.15) | 2.548 (42.06) | 2.046 (29.19) | 2.548 (35.76) | 3.146 (37.86) | 2.547 (42.87) |
| pp_sin_ass | -0.002 (-2.18) | -0.002 (-2.17) | -0.002 (-2.68) | -0.003 (-3.22) | -0.003 (-3.27) | -0.003 (-3.04) | -0.002 (-2.61) |
| vph_sin_ag | 0.011 (14.51) | 0.011 (14.77) | 0.012 (15.33) | 0.011 (14.53) | 0.011 (14.34) | 0.010 (13.80) | 0.011 (15.25) |
| graproes_f | -0.056 (-9.36) | -0.056 (-9.46) | -0.069 (-11.18) | -0.08 (-12.42) | -0.075 (-12.11) | -0.076 (-12.65) | -0.066 (-10.81) |
| log_pob | 0.018 (2.92) | 0.022 (3.54) | 0.028 (4.16) | 0.031 (4.09) | 0.027 (3.85) | 0.028 (4.22) | 0.025 (3.88) |
| lag.pp_sin_ass | 0.001 (1.63) | 0.001 (1.24) | |||||
| lag.vph_sin_ag | -0.003 (-4.27) | -0.001 (-1.14) | |||||
| lag.graproes_f | 0.047 (7.4) | 0.031 (5.27) | |||||
| lag.log_pob | -0.027 (-3.6) | -0.019 (-2.75) | |||||
| P | 0.121 (8.41) | 0.201 (12.91) | -0.228 (-10.46) | ||||
| Lambda | 0.200 (12.44) | 0.201 (12.85) | 0.411 (19.04) | 0.170 (9.43) |
Fuente: elaboración propia a partir de estimaciones realizadas con r-project.
A primera vista, los modelos presentados en el Cuadro 2 son relativamente similares en cuanto a la forma del modelo y los valores de los parámetros evaluados. Sin embargo, difieren significativamente. Los modelos SAR, SAC y SDM contienen un término espacial endógeno, por lo que asumen una dependencia espacial global, mientras que los modelos ESR y SDE contienen un término espacial exógeno y asumen una dependencia espacial local (Anselin, 2003; Halleck Vega & Elhorst, 2015; LeSage & Pace, 2009).
La interpretación de los modelos de regresión, presentados en el Cuadro 4, se basa en las tres propiedades fundamentales de la variable explicativa: (1) ejerce un efecto sobre la variable dependiente, conocido como efecto directo; (2) el cambio sobre la variable dependiente no solo depende de la k-ésima variable explicativa, sino también de las variables explicativas de las unidades vecinas y (3) los efectos indirectos sobre la variable dependiente pueden ser locales o globales.
De manera que la interpretación de coeficientes difiere entre modelos con y sin efectos endógenos. Por ejemplo, en el modelo SAR de (1), la derivada parcial de y respecto a xk produce una matriz N x N que representa el efecto parcial que cada unidad espacial i ejerce sobre sí misma y sobre todas las demás unidades espaciales j, con j # i. Los elementos diagonales de la matriz cuantifican el efecto de cada unidad i sobre sí misma (i.e., el cambio de xi sobre el cambio de yi), y cada elemento fuera de la diagonal representa el efecto de la unidad espacial i sobre las unidades restantes j, con j # i (i.e., cuantifican el cambio de xi respecto del cambio de yj). Así, las entradas de la diagonal de la matriz representan los impactos directos de la variable xk, los que cuantifican el efecto medio de un cambio unitario de xi sobre yi, mientras que los impactos indirectos muestran cómo un cambio en xi influye en promedio sobre las unidades vecinas yj.
Para el caso de los modelos OLS, ESR y SDEM, las estimaciones puntuales obtenidas en los modelos de regresión pueden interpretarse como impactos parciales (directos e indirectos), mientras que en el caso de los modelos SAR, SAC y SDM, las estimaciones puntuales difieren de las derivadas parciales, lo que resulta del hecho de que un término endógeno de la variable dependiente contiene bucles de retroalimentación a través del sistema de vecinos Wy, de manera que un cambio de xi en la unidad espacial i influye sobre sí misma y sobre las unidades vecinas j, y a su vez la unidad i influye en un bucle de retroalimentación. Este bucle de retro-alimentación forma parte del impacto directo. Así, los efectos indirectos de los modelos SAR, SAC y SDM configuran efectos indirectos globales, lo que implica que incluyen efectos sobre vecinos directos, efectos sobre vecinos de vecinos (vecinos de segundo orden) y efectos sobre los vecinos de segundo orden hacia vecinos de orden superior, mientras que los modelos ESR y SDE presentan efectos indirectos locales (LeSage & Pace, 2009).
Los impactos indirectos locales representan el efecto de todos los vecinos definido por W sobre la unidad espacial i (la media de todos los vecinos en el caso de una matriz de pesos normalizada por filas), mientras que los efectos indirectos globales conforman una especie de proceso de difusión, es decir, que un acontecimiento exógeno se difunde globalmente debido a un efecto endógeno.
Cuadro 5 Modelo SAC
| Estimate | Std.Error | z.value | P(z) | |
|---|---|---|---|---|
| (Intercept) | 3.146 | 0.083 | 37.878 | 0 |
| pp_sin_ass | -0.003 | 0.001 | -3.051 | 0.002 |
| vph_sin_ag | 0.01 | 0.001 | 13.777 | 0 |
| graproes_f | -0.076 | 0.006 | -12.614 | 0 |
| log_pob | 0.028 | 0.007 | 4.172 | 0 |
| P | -0.228 | 0.021 | -10.534 | 0 |
| A | 0.411 | 0.021 | 19.117 | 0 |
Fuente: elaboración propia a partir de estimaciones realizadas con R.
Para el caso particular, la variación de la mortalidad infantil intermunicipal se explica a partir del modelo de regresión espacial (SAC) que modela los efectos que las variables explicativas ejercen entre municipios vecinos mediante el vector de rezago espacial Wy, el cual refleja los niveles promedio de las variables estudiadas a nivel municipal, a través de la matriz de pesos espaciales W, mientras que el parámetro p evalúa la intensidad de la dependencia espacial y el parámetro LAMBDA. Intuitivamente, el modelo precisa la forma como los niveles de carencia de acceso a servicios salud, agua, escolaridad femenina y tamaño de población están relacionados con la mortalidad infantil (véase Cuadro 2). Cuando p y X son estadísticamente iguales a cero, el modelo SAC se transforma en un modelo de regresión lineal simple (OLS). En nuestro caso, ambos parámetros resultaron ser estadísticamente distintos de cero.
Es importante señalar que el modelo SAC une un proceso autorregresivo de dependencia espacial y un proceso autorregresivo del error espacial (Tiefelsdorf, 2000). La dependencia espacial del error tiene su origen en variables no observables que se encuentran correlacionadas espacialmente; cuando esto ocurre, se recomienda ajustar un modelo espacial SAC. En el Cuadro 5 se presentan los resultados de la aplicación del modelo SAC a los datos espaciales de mortalidad infantil para los municipios de México en el año 2020. Se observa que tanto el parámetro X de error espacial como el parámetro p de dependencia espacial resultaron estadísticamente significativos, al igual que todas las covariables introducidas al modelo, lo que da sentido a su implementación.
La interpretación de los coeficientes ß permite comprobar la existencia de dependencia espacial, ya que cuantifica el cambio de una variable independiente, ocurrido en los vecinos del municipio i, que incide sobre la variable dependiente del municipio i. Los cambios en las características de los municipios vecinos generarán a su vez alteraciones en la dinámica de los municipios aledaños a i y viceversa.
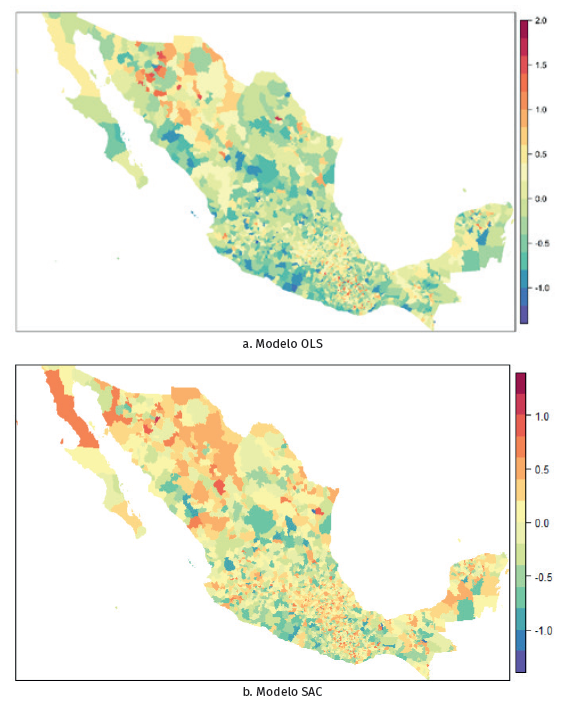
Fuente: elaboración propia a partir de estimaciones realizadas con R.
Mapa 7 Residuos del modelo de regresión lineal (OLS) vs. modelo de regresión espacial (SAC).
Así, el efecto directo proporciona una medida sintética de los efectos de los coeficientes, es decir que, si en el municipio i se incrementan los niveles de escolaridad de las mujeres, el efecto directo cuantifica el impacto promedio sobre la tasa de mortalidad infantil del municipio. Esta medida toma en cuenta los efectos de retroalimentación que surgen a partir de cambios en el nivel de escolaridad de la madre en el municipio i y el impacto de sus vecinos a través del sistema de dependencias espaciales conformado por la matriz W. Esto significa que el efecto directo de la mortalidad infantil municipal indica que un crecimiento de un punto en la carencia por acceso a servicios de salud -en el municipio, como se menciona en Hernández y Narro (2019), y Méndez (2006)- i) provoca una reducción de 0.003 puntos porcentuales de la tasa de mortalidad infantil.
El efecto directo más importante generado por el modelo SAC proviene de los años promedio de escolaridad de las mujeres (Álvarez et al., 2009), donde el incremento promedio de un año de educación implicaría una reducción de 0.076 puntos porcentuales en la tasa de mortalidad infantil municipal (Duarte-Gómez et al., 2015). Es importante señalar que el comportamiento de la mortalidad infantil municipal en todos los modelos es inverso al incremento de la escolaridad de las mujeres, como se observa en Arriaga (1996), por lo que, al incrementar los niveles de escolaridad, se esperaría invariablemente observar una reducción significativa en los niveles de mortalidad infantil municipales (Cuadro 2). En el mismo sentido deben interpretarse los efectos generados por las variables de la carencia de acceso a agua y el porcentaje de población municipal (Duarte-Gómez et al., 2015).
El uso de métodos econométricos espaciales se fundamenta en la violación de supuestos asociados a la validez de los modelos de regresión (Álvarez et al., 2019), en particular, el supuesto de auto-correlación espacial de los residuos, los cuales deben presentar una distribución aleatoria sobre el área de estudio, lo que puede interpretarse como un efecto aleatorio espacial. Una de las formas más comunes de evaluar este supuesto es utilizando mapas.
En términos generales, la distribución de residuos generados por modelos espaciales y por modelos no espaciales difiere considerablemente. Se espera observar patrones espaciales de concentración o dispersión de residuos en los modelos no espaciales (ver Mapa 7a), mientras que se esperaría observar un patrón aleatorio en los residuos generados por modelos espaciales. Así, el mapa de distribución de residuos del modelo OLS muestra, como se suponía, grupos de residuos grandes, especialmente alrededor de las costas de Guerrero y Sinaloa, lo que indica que el modelo presenta problemas de autocorrelación espacial. En contraste, el Mapa 7b presenta un patrón de distribución espacial de residuos mucho más disperso; no obstante, el modelo SAC no fue capaz de eliminar por completo la autocorrelación espacial de los datos, lo que puede deberse en otras cosas a la omisión de alguna variable explicativa.
CONCLUSIONES
El modelo de regresión econométrica espacial SAC permitió cuantificar las diferencias observadas en los niveles de mortalidad infantil municipales, debidas a la carencia de acceso a servicios de salud, a la carencia de agua dentro de la vivienda, años promedio de escolaridad femenina y tamaño de población. En general, las variables hicieron posible cuantificar los diferenciales en mortalidad infantil entre municipios. Es decir, el trabajo posibilitó valorar la importancia de la heterogeneidad espacial en la determinación de los niveles de mortalidad infantil en los municipios de México.
Los resultados mostraron la importancia de las condiciones socioeconómicas para explicar el comportamiento territorial de la mortalidad infantil. El modelo espacial SAC demostró la trascendencia que tiene el nivel de escolaridad de las mujeres y como un efecto espacial para reducir las tasas de mortalidad infantil, seguido por el tamaño de población, la carencia de acceso a servicios de salud y la carencia de acceso al agua dentro de la vivienda; situación que implica que, para entender el comportamiento espacial de la mortalidad infantil municipal, es importante considerar la existencia de patrones de desigualdad en la distribución de la infraestructura educativa, la formación de patrones de acceso a servicios de salud y agua, y el efecto del tamaño de la población.
El estudio destaca la importancia de los niveles de educación femenina, como un elemento fundamental para la reducción de los niveles de mortalidad infantil, y cuestiona seriamente el papel de las instituciones como responsables de materializar los servicios educativos e incrementar el nivel educativo de las mujeres; en particular en los municipios donde se observan los mayores niveles de mortalidad infantil. Los resultados demuestran especialmente asimetrías significativas entre municipios donde se observa una relación inversa entre el incremento de escolaridad femenina y la reducción de la mortalidad infantil, de forma que resulta obvio que, para reducir las tasas de mortalidad infantil en los municipios de México, es necesario mejorar el nivel de educación de las mujeres, elevar los niveles de acceso a servicios de salud, ampliar los programas de dotación de agua en las viviendas, así como desarrollar estrategias de ordenamiento territorial que permitan reducir los niveles de dispersión y concentración poblacional observados en gran parte de los municipios de México.