Luis E. Arango**
Carlos E. Posada*

* Economic Research Unit, Banco de la República. The opinions expressed here are those of the authors and not of the Banco de la República nor of its Board of Directors. We thank Adriana Camacho, John James Mora and two anonymous referees for comments and sug­gestions and Lina Cardona for research assistance and suggestions. Any remaining errors are solely ours.

** Luis E. Arango. E-mail address: larangth@banrep.gov.co, Banco de la República, Carrera 7ª No. 14 – 78, Piso 11. Telephone number ++ 57 1 3430676. Fax ++ 57 1 3421804.

This paper was received June 8, 2007, modified November 30, 2007 and accepted December 10, 2007.

Abstract

A pseudo-panel was built to estimate the determinants of the labor participation decision of married women between 1984 and 2000 in Colombia. Past participation decisions, education level, labor income taxes, children aged between 1 and 2 years old, and the presence of other people unemployed at home are the main explanatory variables of married women's labor participation. The interest rate does not have any effect on that decision.

Key words : married women, labor participation, state-dependence, fertility.

JEL Classification : C21, C23, C25, J22, J13.

Resumen

Se construyó un pseudo-panel para estimar los determinantes de la decisión de participar de las mujeres casadas entre 1984 y 2000 en Colombia. Las decisiones de participación pasadas, el nivel educativo, los impuestos al ingreso laboral, los niños entre 1 y 2 años de edad y la presencia de otros desempleados en el hogar son las principales vari­ables explicativas de la participación laboral de las mujeres casadas. La tasa de interés no tiene ningún efecto en dicha decisión.

Palabras clave : mujeres casadas, participación laboral, dependencia de estado, fertilidad.

Clasificación JEL : C21, C23, C25, J22, J13.

Introduction

The decision of joining to the labor force is a topic that has deserved a sizeable amount of research in economics (see Heckman, 1993; Blundell and Macurdy, 1999; Pencavel, 1986). Noticeably, a signifi­cant fraction of the research in this area has been devoted to the study of the participation of married women (see Mincer, 1962; Gronau, 1973; Killingsworth and Heckman, 1986, among many others). This is because such a decision of married women has represented some im­portant challenges to researchers that have sometimes been adequately captured by both economic models and econometric methods. Related to these challenges we may mention the proxies that have been used for the potential market wage (human capital acquisitions, experience, age, probability of transitory leaves for fertility decisions, etc.) and the reservation wage (non-labor income, including the husband's wage, fertility decisions, in particular, the presence of young children and the cost of child care, etc.).

Labor participation in Colombia has been studied, from a static point of view, using the independent cross-sections data provided by the National Household Survey (NHS) (see Tenjo and Ribero, 1998; López, 2001; Santamaría and Rojas, 2001; and, Arango and Posada, 2005). The results of these studies are convergent in terms of the participa­tion determinants.

Intertemporal models of labor supply have been implemented to capture the behavior of participation within a life-cycle framework (see among others, Heckman and MaCurdy, 1980; MaCurdy, 1981; Goldin, 1982; Altonji, 1986) taking into account aspects related to state dependence, persistence, asset accumulation, interest rates, labor income taxes, and fertility. Unfortunately, for the case of Colombia, there is a lack of research that focuses on the life-cycle behavior of the extensive margin of the labor supply regardless of the advantages of this approach. The explanation of this shortage may be in the fact that, in Colombia, there is no panel data on labor participation and household´s income. In spite of this weakness of Colombian statistics, Sánchez and Núñez (2002) undertook a pseudo-panel approach to study some household behavior characteristics including labor force participation. The empirical work of Sánchez and Núñez addresses a fair amount of aspects of the households such as the structure and size of the family, stock, investment and returns of human capital, and participation rates. The main contribution of this article consists of the number of stylized facts on each of the aforementioned aspects that it shows for the Colombian case.

In this work, following Deaton (1985) a pseudo-panel is conformed in order to observe some life-cycle properties of labor force participa­tion. Independent cross-sections, based on the quarter stages of NHS for the seven biggest cities between 1984 and 2000, are transformed into population cohorts; the sample mean of each cohort is computed and used as a panel. Then different models of participation for married or in common-law unions women are estimated to asses the main deter­minants of the labor participation decision.

The model attempts to capture the behavior of labor participation over time, the main recent findings related to fertility decisions (see Nakamura and Nakamura, 1992; Carrasco, 1998; Chun and Oh, 2002; Attanasio et al. 2004, etc.), the problem of initial conditions (Wooldridge, 2002) and the so called memory of labor participation decisions (true state depend­ence) (Heckman, 1981; Hyslop, 1999; Carro, 2003; etc.).

In this set up, of particular interest is the possibility of considering in the analysis the number of children by age to face any potential endogeneity of the participation decision. Nakamura and Nakamura (1992) surveyed empirical aspects of female labor supply and children. Apart from ex­plaining direct and indirect effects of children status in the participation decision they also present the instrumental variables approaches used to deal with the endogeneity. Among the main conclusions of Nakamura and Nakamura are, in first place, that fertility (having a baby or a child) reduce the probability of a woman being unemployed although this ef­fect is lower than it was believed from previous studies, and, in second place, that the instrumental variables approach has a few shortcomings with respect to a number of child status dimensions.

Also of interest are the concepts of state dependence and persistence. The first, as stated by Heckman (1981), suggests that as a consequence of a previous episode, preferences, prices, or constrains relevant to future choices or outcomes are modified. As a result, the behavior of an indi­vidual that experienced the event will be different from an, otherwise, identical individual that did not experience it. The concept of persistence is identified by Heckman (1981, p. 91-92) with the difference among individuals in a number of unmeasured variables that could be affecting their probability of experience the event but are not influenced by the experience of the event. In the hypothetical case that these variables are autocorrelated, and this property is not controlled, the past experience may appear as a determinant of subsequent experience just because it is a composite of such temporally persistent unobservables.

This article develops as follows: Introduction. Section I establishes the characteristics of the models both theoretical and empirical. Section II shows some key aspects of the cohorts and some stylized facts derived from the pseudo-panel analysis. Section III explains the empirical ap­proach and presents and discusses the results. Finally, Section IV draws some conclusions.

I. A model for labor participation over time

The aim of this paper is to check the power of some potential deter­minants of married women's labor participation when they make this decision during the course of their lives. Among the determinants are interest rates, labor income taxes, education level, age, non-labor income, and the cost of child care, this latter factor being neatly connected to fertility decisions. This section develops a model in which these variables appear as the determinants of the extensive component of the labor supply¹.

Consider a married woman whose problem is to maximize the present value of discounted utility over a finite lifetime:

where O is a monotonically increasing function, u(×) is the periodic utility flow, a is the discount factor, c_t is consumption at age t, total hours available for the woman are normalized to 1 and used to work in the market, n_t, or leisure time, l_t, so l = n_t + l _t, and, x_t is a vector of characteristics of the family in period t, which accounts for observed and unobserved heterogeneity both over time and across families. If the woman decides to work she will undergo a welfare loss but, on the other hand, the labor income will allow her to increase consump­tion. If she decides to work, her after-tax income net of the costs of childcare and some others is:

where w_t is the wage, y_t the non-labor income, t_t the labor income tax rate, d_t the fraction of the wage's present value that she undergoes in the future if she decides not to work in the present. In other words, d_t is the depreciation rate of human capital², f_t the cost of substitut­ing direct child attention for indirect attention, and l_t the job search cost which is associated to the leisure time of the previous period³.

The specification in (2) means that if the married woman decides not to work in period t her income will be: y_t - d_tw_t(1 - t_t) - l_t(1 - n_{t - 1}). The objective is to maximize (1) subject to the constraint:

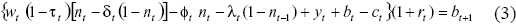
where b_t is the amount of assets at the beginning of period t +1 and r_t is the interest rate. This restriction assumes that the woman can save any surplus and acquire debts⁴.

The solution to the problem implies that she is indifferent between participation or nonparticipation in the labor market at the corner where 1 = l_t if the wage that she would receive in the labor market w_t is equal to the reservation wage, _t, plus the job search costs. In other words, an interior solution will exist if w_t > + l_t(1 - n_{t - 1}).

The period t decision, conditional on current and future realizations of the exogenous variables, can be defined by:

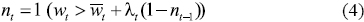
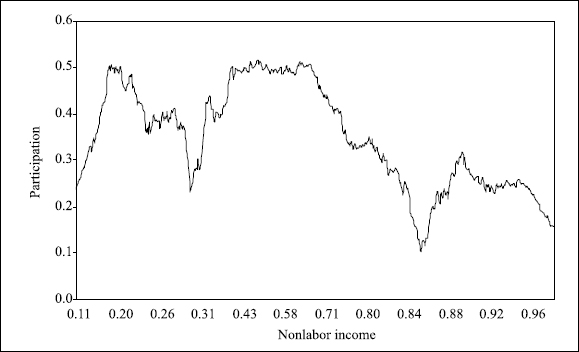
where 1(.) is the indicator function that is equal to 1 if the expression is true and 0 otherwise. Empirically, if we reparameterize by using l* instead of l_t to express search costs in terms of participation (or hours) rather than in terms of leisure, the theoretical model (4) considered for woman i in period t is:

where X_it is a vector of observed variables intended to represent the market wage and the reservation wage of woman i in time t, such as family composition, education level, other dimensions of human capital, and demographic aspects (age, ethnicity, fertility variables, nonlabor income, etc.) while m_it represents the effect of unobserved de­terminants that may affect the participation decision. This unobserved heterogeneity term m_it might be composed by two elements. One which is time invariant that would reflect heterogeneity among individuals possibly originated in human capital and other cohort factors denoted by j_i and one associated to random transitory movements in wages denoted by n_it. This term could be serially correlated but independent of X_it for consistency.

The specific relationship between fertility and labor participation of married women is not that obvious in the sense that these choice vari­ables affect each other. Econometricians have tried to overcome any potential endogeneity among them through the use of instruments like infertile families, or the presence of twins (multiple births), etc. How­ever, the instruments currently used are not satisfactory (Nakamura and Nakamura, 1992) and, consequently, the correct set of instruments remains as an open question⁵.

Another concern that we try to capture is the memory of current labor participation; that is, we try to answer the question whether the contem­poraneous decision on participation depends or not on previous deci­sions about participation in the labor market. This apparent memory may be due to both structural state dependence of female participation and serial persistence of unmeasured variables that may affect the probability of participation. As pointed out in Introduction, Heckman (1981) has made some distinctions between serial correlation and true state dependence being the former associated to persistent individual heterogeneity (see also Hyslop, 1999). The restriction in expression (3), where past participation decisions do have effects, allows our model to introduce the concept of decision memory into play⁶.

II. Data construction and empirical facts

In Colombia there is no panel survey on household labor supply sta­tistics. Thus, to explore the life-cycle implications of the neoclassical model an alternative is to build a pseudo-panel. Such an artificial ar­rangement of household data was built with the information from all stages (quarters) of the National Household Survey (NHS), which are independent cross-sections applied between 1984 and 2000 to compile labor market information⁷. With this pseudo-panel data analysis we expected to track cohort means (supposedly representing a particular married woman) over time a task that would not be possible with independent cross-sections.

To build the pseudo-panel we invoke the approach of Deaton (1985) through which the population is divided into different groups, or co­horts , to depict a representative (average) agent for each group. Thus, instead of observing different true individuals over time we track means derived from the cohort⁸. In our particular case, we focus on six specific groups of women who were born between 1941 and 1970 as presented in Table 1. These cohorts of married women are observed through the period of the NHS ; that is over 68 quarters, between 1984 and 2000. Each cohort consists of women that were born within an interval of years.

To give an idea about the data, let us consider, for example, women that were born in the interval 1941 - 1945 in which we found 1053 people in average. The highest number of observations in a quarter was 2173 while the smallest was 521. We regard the average woman within this interval as born in 1943. For all cohorts the average number of observations was 1617, the highest number of observations found in a quarter was 3272 while the smallest was 166; the latter corresponding to women that were born between 1966 and 1970, or in 1968 on average.

Table 1. Data characteristics per cohort.

Source : Authors' calculation based on the National Household Survey (DANE-ENH).

Summary statistics of each cohort (or representative woman) are pre­sented in Table 2 where the behavior of participation rate and years of education as well as the variability of wealth is noteworthy⁹. It is also important to observe that the number of children increases as long as women are younger; for example, the number of children of age between 0 and 1 has been on average higher and gets bigger for women of cohorts 4 to 6.

Table 2. Some characteristics of cohorts.

A number of other salient features of the Colombian labor market can be accounted for. This is the case of participation over time shown in Figure 1. As predicted by the life-cycle model, the rate of participation over time shows an inverted- U behavior: at an early age women par­ticipate less in the labor force, but as long as age and education levels increase, participation also increases. After that some other forces start to affect the decision; for example, the presence of young children, the level of wealth already acquired, and the non-labor income (income of their husbands) reduce the probability of participation. There are, on the other hand, forces, like experience, that increase the probability of labor participation.

Figure 2 shows the labor participation rate of each group according to age. For example, at age of 35-39 years old the representative woman of cohort 2 (G2) has a rate of participation of 40.7%, G3 of 49%, G4 of 55%, and G6 of 66.6%. Notice that at interval of 35-39 years old there were no women born between 1941 and 1945 or between 1966 and 1970 participating in the labor market. From that picture we can observe that labor participation is lower for older groups than for younger ones. That is, when people in Group 3 (G3), who were born, on average, in 1953, were between 30 and 34 years old they participated less than those of Groups 4, 5, and 6 at the same ages. At the same time younger married women tend to participate more in the labor force. Figure 3 shows the participation rate of each cohort over time where the rapid increase in participation of G6 is remarkable. These facts might be evidence of a cohort effect that we will try to address empirically below¹⁰.

Figure 1. The life-cycle of participation rate.

Source : Authors' calculation based on the National Household Survey (DANE-ENH).

Figure 2. Mean of participation rate per cohort.

Source : Authors' calculation based on the National Household Survey (DANE-ENH).

Figure 3. Participation rate per group.

Source : Authors' calculation based on the National Household Survey (DANE-ENH).

Figure 4 shows the behavior of both the participation rate and the number of years of education. The left vertical axis measures the years of education while the right axis measures the participation rate. Thus, we can observe that, up to a scale, there is a similarity in the move­ments of the two variables; even more, the peak of education is reached about two years before the peak of participation rate; after that, both variables start to decline with age. Figure 5 presents the relationship of the participation rate and education. It seems clear that participation increases along with the years of education; however, it also seems that two types of women co-exist with education between 4.5 and 8.5 years: one type that participates, on average, more than 12 percentage points than the other type. This difference is evident between women with 6.5 and 8.5 years of education. The level of wealth is a plausible candidate to explain such a nonlinear behavior.

Figure 4. Behavior of education and participation rates over time.

Source : Authors' calculation based on the National Household Survey (DANE-ENH).

Figure 5. Education and participation rates.

Source : Authors' calculation based on the National Household Survey (DANE-ENH).

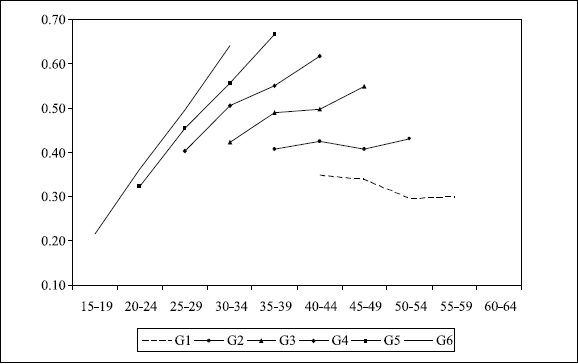
Another typical determinant of labor participation is the wealth or non-labor income usually regarded as one of the main components of the labor opportunity cost or the reservation wage. The wealth of the family is set as a dummy that takes the value of 1 if the family either owned a house (without any outstanding mortgage debt), or the neighborhood is middle class or higher¹¹, or the family earned, in the previous month, $2.500.000 in real terms (Colombian pesos of December 2000); oth­erwise it takes the value of 0. Figure 6 shows the relationship between the participation rate and our definition of wealth. The probability of participation in the labor market starts to decline from about 0.5 when the probability of having wealth is higher than 0.6.

Figure 6. Participation rate and wealth (or nonlabor income).

Source : Authors' calculationbased on the National Household Survey (DANE-ENH).

One of the most interesting aspects of the female participation has to do with costs of childcare and fertility decisions since these variables are also expected to be determinant of women´s reservation wage. Figure 7 shows the participation of married women ordered according to the number of children they have of 6 years old or less. From that picture it seems that participation is low when the number of children is also low, contrary to what the theory postulates. To disentangle this counterintuitive fact we decompose the children under 6 year old into six categories: children between age 0 and 1 years old, between 1 and 2, 2 and 3, 3 and 4, 4 and 5 and, finally between 5 and 6 years old. Figure 8 shows the number of children classified according to age. Thus, 19-year-old mothers have, on average, 0.536 children between ages 0 and 1 years old, 0.182 children between ages 1 and 2 years old, and so on. The implication that emerges from this picture is that younger mothers have younger children.

Figure 7. Number of children aged six years old or less and mother's participation.

Source : Authors' calculation based on the National Household Survey (DANE-ENH).

Figure 8. Number of children per mother and mother´s age.

Source : Authors' calculation based on the National Household Survey (DANE-ENH).

Fertility poses a challenge to the analysis of labor participation since endogeneity might be present (Nakamura and Nakamura, 1992). That is, labor participation might affect current or future fertility decisions and vice versa. Given the evidence obtained from Figures 9, 10 and 11, we observe some potential to this point. Figure 9 presents the labor participation behavior of mothers who have at least one child between ages 0 and 1 and no children at any other age. This figure also shows the labor participation of mothers who have at least one child between 1 and 2 years old, and the labor participation of mothers who have at least one child between 2 and 3 years old at all ages of mothers. It seems evident that the labor participation rate of mothers who have children only between ages 0 and 1 is always lower than that of moth­ers who have children only between ages 1 and 2, and with children only between ages 2 and 3. This result is the same for mothers with children only between ages 5 and 6. At this children's age their moth­ers decide to reduce labor participation in comparison to mothers with children between 3-4 and 4-5 years old (Figure 10).

Figure 9. Participation rate of mothers with at least one child at ages 0-1, 1-2 and 2-3.

Source : Authors' calculation based on the National Housing Survey (DANE-ENH).

Figure 10. Participation rate of mothers with at least one child at ages 3-4, 4-5 and 5-6.

Source: Authors' calculation based on the National Household Survey (DANE-ENH).

Figure 11. Participation rate of mothers with at least one child at ages 0-1 and 5-6 and total participation.

Source : Authors' calculation based on the National Household Survey (DANE-ENH).

In Figure 11 we observe that the participation of mothers with children only between ages 0 and 1 and between ages 5 and 6 is similar up until the mother is about 35 years old; the participation rate of mothers older than that is slightly higher for those who have only children between ages 5 and 6 years old. Both of them are lower than total participation. That is, participation is negatively related to fertility decisions: participation rate of married women with children aged between 0 and 1 is less than any other participation rate. Also noticeable, the participation rate of married women declines over time; this is why participation of mothers with children who are older than 5 but younger than 6 is also lower than other participation rates.

III. Econometric issues, results and discussion

The theoretical model of Section I and the facts showed in the previ­ous section gives rise to some hypothesis that one may verify¹². The econometric exercises carried out in this work can be divided into three parts. First, through a time series analysis, we focus on interest rates and labor income taxes as determinants of participation rates. Second, a pooling probit (static) regression is adjusted in order to analyze the determinants within this set where unobserved heterogeneity becomes more relevant. Third, panel data estimations are carried out. In the latter case we use not only the linear probability model to observe the signs and magnitudes of marginal effects under the fixed effects estimator, but also the random effects probit estimator.

A. Time series analysis

With the linear regressions of each cohort in isolation we verify the power of the interest rate factor and labor income taxes¹³ to explain the labor participation decision over time. Both elements are always present in the Euler equation generated by an optimization process. The empirical counterpart we define is given by:

Hence, we use the model and include the past probability of participation (the latent probability¹⁴) which is denoted in Table A1 in the Appendix, as lagged participation. The rest of the variables in Table A1 are inter­est rates, labor income taxes, years of education, non-labor income (or wealth) defined as a dummy variable that takes the value of 1 if the condi­tions mentioned above for the family hold and 0 otherwise, presence of other people unemployed at home which is a dummy variable that takes the value of 1 if there are people undergoing unemployment episodes and 0 otherwise, squared age (our proxy of human capital depreciation), and the number of children under age 6. The regressions in Table A1 focus on Groups 3 to 6 given the variability of the dependent variable.

The estimates corresponding to past latent participation and presence of others unemployed at home are significant for most of the cohorts. But the lack of significance of the coefficients associated to interest rates, labor income taxes, and the number of children under age 6¹⁵ is noticeable.

To check again the relevance of our intuition, we disaggregate the vari­able children under age 6 to verify the explanatory power of fertility. This is replaced by children of ages between 0 and 1 year old, between ages 1 and 2, 2 and 3, 3 and 4, 4 and 5, and 5 and 6 years old. In this case we have disregarded the variable "age" since the inclusion of chil­dren at different ages could induce some collinearity between mothers age and the number of children. Table A2 presents the results of these regressions which are, again, focused on cohort 3 to 6 given the vari­ability of the dependent variable¹⁶. There are two regressions which differ only because the first includes children between ages 0 and 1 while the second does not.

The results in Table A2 (see the Appendix) show that past latent partici­pation probability is not significant for Groups 3, 4, 5, and 6. This is also the case with interest rates and labor income taxes, but interestingly, and irrespective of the significance, the corresponding coefficients of those variables take different signs showing different dominance of substitu­tion and income effects depending on the group we are looking at. Labor income taxes are significant for cohorts 3 and 6 with signs negative and positive, respectively, giving some evidence of dominance of substitu­tion effect in the first case and income effect in the second.

With respect to children, now disaggregated by age, there is a gain since for each group we can observe which of them affect the labor participa­tion decision. However, no interesting pattern arises from these regres­sions because the coefficients are not significant and sometimes the sign of those coefficients is different from the expected one. In summary, the time series approach to the labor participation decision is not illuminating enough about its determinants during the sample period for the artificial cohorts we have built.

B. Pooled probit regression

A second approach we undertake is a pooling probit regression to analyze the effect of unobserved heterogeneity. Since all observations are put altogether the model cannot show any dynamics such as the memory of the dependent variable as one of the explanatory variables. For this reason, the model is:

The results of this regression are included in the first two columns of Table 3 where we can observe that some of the estimated probit coef­ficients have the expected sign. This is the case of education, labor income taxes, non-labor income, other people unemployed at home, squared age, children of between ages 0-1, 1-2, 4-5, and 5-6 years old. However, the coefficients of children of between ages 2-3 and 3-4 do not correspond to the predictions of the theory. As we mentioned above, both labor income taxes and interest rates can generate substitution and income effects. According to the sign, the former seems dominates in the case of the two variables. As for the interest rate, the sign and sig­nificance of the estimated coefficient suggest that married women will reduce the probability of participation in the labor market when the interest rate increases.

Table 3. Pooled Probit.

Note: standard errors are in parenthesis.

However, not all the above coefficients are significant. This is most noticeable in the cases of labor income taxes, non-labor income, and children between ages 2-3, 3-4 and 5-6. Based on the coefficients and the proxy variables we have used, the probit model seems to be close to the theory and give some importance to unobserved heterogeneity since coefficients linked to fertility are now significant. However, regardless of having the signs predicted by the theory, the marginal effects analysis suggests that no variable is really significant in the model for the whole sample period. However, for a shorter period of time (1990:1-2000:4), education and others unemployed at home, as evidence of the "additional worker effect", are significant on the grounds of marginal effects.

C. Panel analysis

Participation decisions pose a number of problems such as the treatment of unobserved heterogeneity either as fixed or random, the incidental parameters problem, the potential endogeneity of fertility decisions¹⁷ (especially in the case of married women), the serial persistence-state dependence phenomena, and the initial conditions for the dynamic proc­ess given the intrinsic nonlinearity of a probit model. Consider again Equation (5) which is written here for convenience:

where the term m_it, referred to unobserved heterogeneity, is composed by two elements as we stated above: j_i and n_it. The first represents heterogeneity among individuals originated in factors such as human capital and other cohort factors and the second associated to random transitory movements in wages as in Hyslop (1999). The fixed effects probit model regards j_i as parameters to be estimated together with b since this procedure does not require any assumption about the distribution of j_i given X_it. Unfortunately the joint estimation of j_i and b generates the incidental parameters problem. This difficulty arises because of the nonlinear underlying nature of the probit model which leads to inconsistent log-likelihood estimation of b with T fixed and N ® ¥ (see Wooldridge, 2002, chapter 15). In other words, the estimation of b could change as long as new observations are added to the sample.

The dynamics of the labor participation, observed through the high degree of memory, is an important characteristic of this individual´s decision. Associated to the memory of participation are the problems of initial conditions and persistence-state dependence. The former arises since the participation process is not observed at the moment of entrance to the labor age (which takes place in Colombia when people are at least 12 years old) and, as a result, an assumption has to be done about the first decision of labor participation (n_i0) and its relationship to other determinants. A misspecification of the initial conditions will also lead to inconsistent estimates of b. To deal with this issue, given the random effects approach used, we follow the procedure of Wooldridge (2002) which decompose m_it into j_i , n_i0, X_i and z_it.

As for the serial persistence problem, the literature recognizes a dif­ference between state dependence and persistence. The former is explained on the basis of human capital accumulation and job search costs¹⁸; these are reasons to observe that individuals, with some ob­servable characteristics, decide for an option with higher probability when they have made the same decision in the immediate past (true state dependence). The latter might be caused by persistent individual unobserved heterogeneity through which there is a high probability to take a labor participation decision but without regard to the determi­nants of previous choices.

Then, focusing on the estimation, if we assume for the moment that n_it is serially uncorrelated, it could be of some interest to consider the fixed effect linear probability model which has the appeal that, as stated above, it does not make any assumption on the distribution of j_i . This model controls for any arbitrary correlation between j_i and X_it and can help to eliminate the incidental parameters due to the form of controlling for unobserved heterogeneity which consists of differencing the processes. A disadvantage of the linear probability model is that one can account for the fact that its forecasts are not restricted to the [0, 1] interval. For this exercise we restrict ourselves to the shorter sample period and use the variables that (according to previous exercises) have more potential. At the same time, to avoid the problem of potential endogeneity between the labor participation decision and fertility we discard the children between 0 and 1 years old taking into account that past participation probability has been included as an explanatory variable. Results in Table 4 suggest that the performance of this model is rather poor in terms of significance of the estimated coefficients and the sign of the coefficient corresponding to education. For the fixed effects model, the r coefficient is high enough (0.5361), which indicates that the variability explained by the fixed component of the model is important to some extent.

Table 4. Linear Probability Model (1990:1-2000:4).

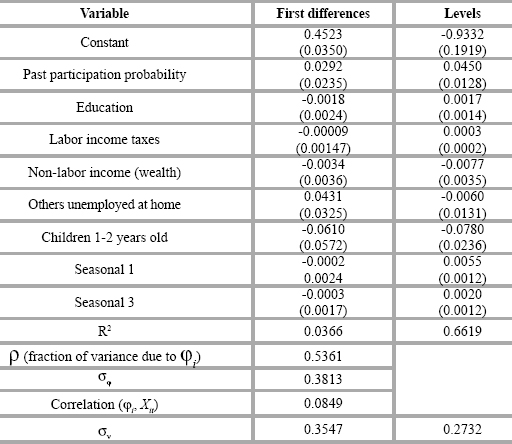
Note: standard errors in parenthesis.

Then we estimate a linear probability model assuming that j_i is not cor­related to X_it, or that m_it is a correlated random effect (model in levels in Table 4). In this case, not only the significance but also the sign and the magnitude of the estimates coefficients change with respect to the fixed effect linear probability model. The random specification suggests that, after controlling for seasonal effects, past participation, non-labor income, and children between ages 1 and 2 years old are the main deter­minants of married women's participation (see Table 4). However, the results must be interpreted with some caution given the length of time (T) versus the size of individuals (N).

Under the assumption that m_it is a correlated random effect we can use probit models. This kind of models parameterize the distributions of j_i . Table 5 shows that, controlling for initial conditions and seasonal effects, there is evidence of true state-dependence. The coefficients of all variables have the sign predicted by the theory and, except for non-labor income, are significant. Nevertheless, according to the r coefficient, the panel effect is not clear, and the specification might be closer to a pooled probit. The marginal effects are significant for all variables and have the expected sign, which suggest that the variables are relevant. In summary, once the set of variables included in the model of Table 5 are had into account the cohort effects vanishes.

Table 5. Panel Probit: Random Effects (1990:1-2000:4)

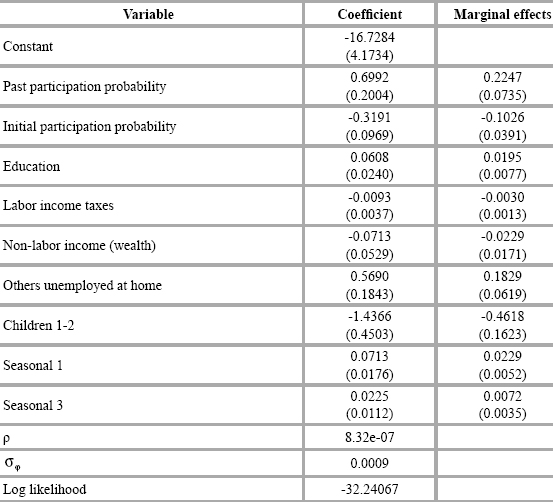
IV. Conclusions

This paper analyzes the labor participation decision of married women in Colombia within a life-cycle framework. By employing the information of the NHS we built a pseudo-panel and end up with 6 groups that we regard as 6 different women. Given the difficulties posed by this topic we undertake an exploratory tour by using different specifications that allow us to arrive at some conclusions.

Some important facts can be sketched directly from the data. This is the case of the behavior of participation curve which takes the form of an inverted- U as age of women increases. Another finding is related to higher participation rates in the labor market of younger women, a fact possibly linked to their higher education level. The data also suggests a negative relationship between participation and wealth and a negative effect of fertility on the participation decision.

Within a neoclassical framework, variables such as interest rates, labor income taxes, education, wealth (non-labor income), presence of others unemployed at home, squared age, and fertility, represented by children of ages from 0 up to 6 are used to model the participation decision of married women.

The effects of the variable Children under age 6 years old, when considered as an entire group (all children of that age or less), are not significant. The same conclusion is obtained with wealth; however, this variable appears most of the time with the expected sign. According to the econometric results intertemporal decisions based on the behavior of interest rates are not relevant for the participation decision.

After controlling for seasonal effects, memory of decisions (structural state dependence) of labor participation is an important variable as well as education, labor income taxes, the presence of other people unemployed at home, and children between ages 1 and 2. When this set of explanatory variables is included into the model, unobserved heterogeneity does not play any role in determining the participation of married or in common-law union women.

Appendix. Time series regressions for participation decision of married women

Table A1. Coefficients of models of cohort participation over time.

Table A2. Coefficients of models of cohort participation over time.

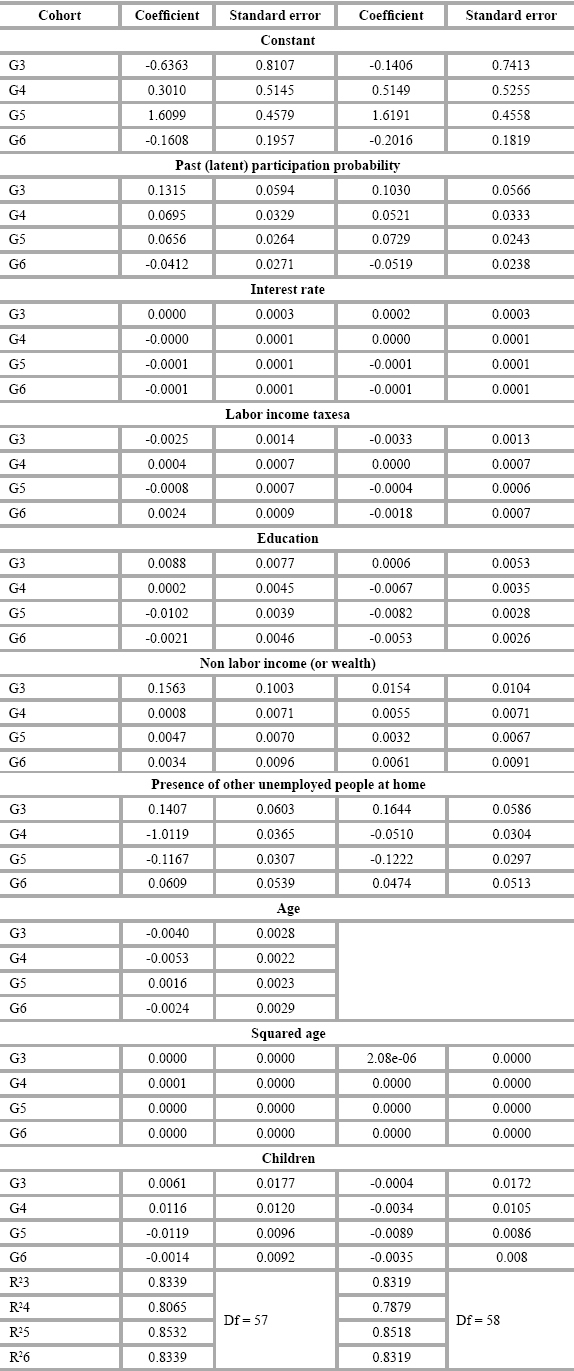
NOTAS AL PIE

1. This model compiles elements of Carrasco (1998), Hyslop (1999), and Attanasio et al. (2004).

2. This term could also be associated to the indirect effects of fertility explained by Nakamura and Nakamura (1992).

3. This set up in the dimensions of depreciation of human capital and search costs allows us to consider true state dependence.

4. The usual terminal conditions that rule out suboptimal decisions are assumed to hold., PP. 93-126.

5. As noted by Carrasco (1998) a number of instruments have been used in the literature many which are correlated with fertility but it is not clear that they are not correlated with the participation decision. She writes: "Religion, number of siblings, ideal family size, and duration of marriage are all probably related to social class, which will affect participation via education and wages".

6. Apart from fixed costs incurred by labor force entrants (search costs), human capital invest­ment acquired through on the job training and depreciation of human capital would give rise to the presence of structural state dependence (see Heckman 1981).100

7. Since the year 2000, the National Agency of Statistics in Colombia (DANE) has been cap­turing information from the labor market through other mechanisms called the Continuous Household Survey, between 2000 and 2006, and Large Integrated Household Survey, since 2006.

8. Collado (1997) argues that when the cohort sample means are used as panels these are subject to measurement errors.

9. The figures correspond to averages along the quarters of NHS.

10. Such a cohort effect was also evidenced by Sánchez and Nuñez (2002).

11. According to the official urban classification system.

12. Following Deaton (1985), given that cohorts are very different in size each observation has been weighted by square root of the cohort size.

13. The series of labor income taxes was kindly provided by L. Fergusson which was first presented in Fergusson (2003).

14. Instead of using the past observed decision (which takes the value 0 or 1) we use the latent or underlying probability of participation.

15. The coefficients corresponding to interest rates and taxes could exhibit any sign depending on the dominance of income and substitution effects that each variable in turn might generate. In the case of interest rate if substitution effect dominates the sign of the coefficient will be positive and people will participate more while in the case of income taxes if the sign of the coefficient is positive the income effect is dominating.

16. The dependent variable of cohorts 1 (G1) and 2 (G2) takes always the value of 0.

17. This problem is not addressed here on the grounds that the set of instruments currently used in the literature is not satisfactory (Nakamura and Nakamura, 1992). However, children between ages 0 and 1 are not included in the regressions when state dependence is explicitly considered.

18. Non-separability of preferences is also a possible source of state dependence.

References

1. ALTONJI, J. G. "Intertemporal substitution in labor supply: Evidence form micro data", Journal of Political Economy, 94(3), (1986), pt 2, s176-S215.        [ Links ]

2. ARANGO, L. E. and POSADA, C. E. "Labour participation in Colombia", Applied Economics, 37, (2005):1829-1838.        [ Links ]

3. ATTANASIO, O. H. Low, and SANCHEZ-MARCOS, V. Ex­plaining changes in female labour supply in a life-cycle model, http://www.homepages.ucl.ac.uk/~uctpjrt/als_fin.pdf, March, (2004).        [ Links ]

4. BLUNDELL, R. and MACURDY, T. "Labor supply: A re­view of alternative approaches", Handbook of labor economics (pp. 1559-1695), vol. 3A, North-Holland, Amsterdam, (1999).        [ Links ]

5. CARRASCO, R. "Binary choice with binary endogenous re­gressors in panel data: Estimating the effect of fertility on female labour participation", Working Paper CEMFI, 9805, (1998).        [ Links ]

6. CARRO, J. M. "Estimating dynamic panel data discrete choice models with fixed effects", CEMFI Working Paper No. 0304, (2003).        [ Links ]

7. COLLADO, M. D. "Estimating dynamic models from time series of independent cross-sections", Journal of Econometrics, 82, (1997):37-62.        [ Links ]

8. CHUN, H. and OH, J. "An Instrumental variable estimate of the effect of fertility on the labour force participation of married women", Applied Economics Letter, 9, (2002):631-634.        [ Links ]

9. DEATON, A. "Panel data from time series of cross-sections", Journal of Econometrics, 30, (1985):109-126.        [ Links ]

10. FERGUSSON, L. "Tributación, crecimiento y bienestar: el caso colombiano", Documento CEDE, No. 2, (2003).        [ Links ]

11. GOLDIN, C. "Life-cycle labor-force participation of married women: Historical evidence and implications", Journal of Labor Economics, 7(1), (1989):20-47.        [ Links ]

12. GRONAU, R. "The effect of children on the housewife´s value of time", Journal of Political Economy, 81, (supplement), (1973).        [ Links ]

13. HECKMAN, J. "What has been learned about labor supply in the past twenty years?", American Economic Review, 83(2), (1993):116-121.        [ Links ]

14. HECKMAND, J. J. and MACURDY, T. E. "A life-cycle model of female labour supply", Review of Economic Studies, 47, (1980):47-74.        [ Links ]

15. HYSLOP, D. R. "State dependence, serial correlation and he­terogeneity in intertemporal labor force participation of married women", Econometrica, 67(6), (1999):1255-1294.        [ Links ]

16. KILLINGSWORTH, M. R. and HECKMAN, J. J. "Female labor supply: A Survey", in O. Ashenfelter and R. Layard (Ed.), Handbook of labor economics (pp. 103-204), vol. 1, North-Ho­lland, Amsterdam, (1986).        [ Links ]

17. LÓPEZ, H. "Características y determinantes de la oferta la­boral colombiana y su relación con la dinámica del desempleo", in M. Urrutia (Ed.), Empleo y economía (pp.155-192) , Bogotá, Banco de la República, (2001).        [ Links ]

18. MACURDY, T. E. "An empirical model of labor supply in a life-cycle setting", Journal of Political Economy, 89(61), (1981):1059-1085.        [ Links ]

19. MINCER, J. "Labor force participation of married women: a study of labor supply", in H. G. Lewis (Ed.), Aspects of labor eco­nomics (pp. 3-35) , Princeton, N. J., Princeton University Press, (1962).        [ Links ]

20. NAKAMURA, H. and NAKAMURA, M. "The econometrics of female labor supply and children", Econometric Reviews, 1 (11), (1992):1-71.        [ Links ]

21. PENCAVEL, J. "Labor supply of men: A survey", in O. As­henfelter and R. Layard, Handbook of labor economics (pp. 3-102), vol. 1, Amsterdam, North-Holland, (1986).        [ Links ]

22. SÁNCHEZ, F. and NÚÑEZ, J. "A dynamic analysis of house­hold decision-making in urban Colombia, 1976-1998: Changes in household structure, human capital and its returns, and female labor force participation, IADB", Research Network Working Paper #R-449, (2002).        [ Links ]

23. SANTAMARÍA, M., and ROJAS, N. "La participación la­boral: ¿qué ha pasado y qué podemos esperar?", Archivos de Macroeconomía, DNP, 146, (2001).        [ Links ]

24. TENJO, J. and RIBERO, R. "Participación, desempleo y mercados laborales en Colombia", Archivos de Macroeconomía, DNP, 81, (1998).        [ Links ]

25. WOOLDRIDGE, J. M. Econometric analysis of cross-section and panel data. Cambridge, The MIT Press, (2002).        [ Links ]