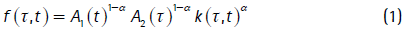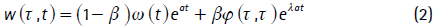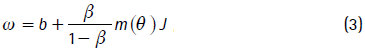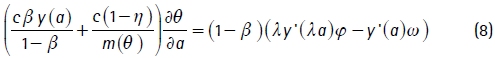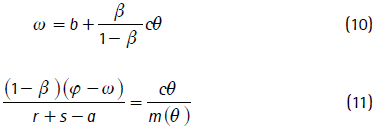Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Desarrollo y Sociedad
Print version ISSN 0120-3584
Desarro. soc. no.73 Bogotá Jan./June 2014
https://doi.org/10.13043/DYS.73.3
DOI: 10.13043/DYS.73.3
Progreso tecnológico y desempleo en Colombia: una aproximación desde los modelos de búsqueda1
Technological Progress and Unemployment in Colombia: An Approximation from the Matching Models
Javier Alfonso Lesmes Patiño2
1 Agradezco los valiosos comentarios y sugerencias de Catalina Gutiérrez, Diana Cárdenas, Ximena Peña, Daniel Poveda y a los evaluadores anónimos de la revista.
2 Magíster en Economía de la Universidad de los Andes. Bogotá, Colombia. Correo electrónico: ja.lesmes21@uniandes.edu.co.
Este artículo fue recibido el 16 de abril de 2013; revisado el 3 de febrero de 2014 y, finalmente, aceptado el 27 de febrero de 2014.
Resumen
En Colombia, la década de los noventa fue un periodo que se caracterizó por incrementos importantes del desempleo, en especial a partir de la segunda mitad de la década. Aunque se han discutido varias razones para tales aumentos, sorprendentemente se le ha prestado poca atención al efecto del progreso tecnológico, el cual, si se mide como el crecimiento de la productividad total de factores (PTF), registró una importante desaceleración para el periodo 1996-2000. Mediante la aplicación cuantitativa del modelo de Pissarides y Vallanti (2007), que es un modelo con crecimiento económico y fricciones en el mercado laboral, este trabajo muestra que la relación negativa entre el progreso tecnológico y el desempleo solo se podría explicar por el dominio del efecto de capitalización, donde menores tasas de crecimiento de la PTF habrían desmotivado la creación de puestos de trabajo y generado un aumento en el desempleo. Sin embargo, se encontró que, aun en el caso extremo en que todo el progreso tecnológico hubiera operado bajo este efecto, la desaceleración de la PTF observada durante el periodo 1996-2000 no logra explicar los incrementos en el desempleo, lo que indica que son otros factores, diferentes al progreso tecnológico, los que explican este fenómeno.
Palabras clave: Desempleo, destrucción creativa, efecto de capitalización, progreso tecnológico.
Clasificación JEL: J64, O33.
Abstract
In Colombia, the nineties was a period characterized by significant increases in unemployment, especially since the second half of the decade. Although several reasons have been discussed in order to explain this increase, it has been given very little attention to the effect of technological progress, which showed a significant measured as the growth of Total Factor Productivity (TFP), it recorded a significant slowdown for the period 1996 - 2000. Through the quantitative application of Pissarides and Vallanti model (2007), that a negative model with economic growth and frictions in the labor market, this paper shows that negative relationship between technological progress and unemployment could only be explained by the dominance of capitalization effect, where lower rates of TFP growth would have discouraged the creation of jobs and generated an unemployment's increase. However, it was found that, even in the extreme case where all technological progress would have operated under this effect, the slowdown in TFP observed during the period 1996-2000 does not explain the increases in unemployment, indicating that other factors different to technological progress are the ones that explain which explain this phenomenon.
Key words: Unemployment, creative destruction, capitalization effect, technological progress.
JEL classification: J64, O33.
Introducción
En Colombia, la década de los noventa fue un periodo que se caracterizó por incrementos importantes del desempleo, en especial a partir de la segunda mitad de la década. La tasa de desempleo colombiana pasó de niveles cercanos al 8% en 1995 al 20% en el año 2000, una de las más altas de América Latina desde la década de los ochenta (Sánchez, Duque y Ruíz, 2009).
Varios factores explicarían el aumento del desempleo en Colombia y quizás los más discutidos han sido los efectos de la legislación laboral, la desaceleración económica de finales de la década, la revaluación de la tasa de cambio y el aumento de la participación laboral (véanse, por ejemplo, Cárdenas y Gutiérrez, 1998; Echavarría, López, Ocampo y Rodríguez, 2011; Núñez y Bernal, 1997; Tamayo, 2008). Los trabajos han encontrado resultados contradictorios con respecto a la tasa de cambio, poca evidencia sobre los efectos del salario mínimo y, si bien hay consenso sobre la contribución de los costos no salariales, la disminución de la demanda y la mayor participación laboral en el incremento del desempleo, aún queda una parte importante de este aumento sin explicar.
Es sorprendente que se le haya prestado poca atención al efecto del progreso tecnológico sobre el desempleo, más aún cuando el progreso tecnológico, medido como el crecimiento de la productividad total de factores (PTF), tuvo desde 1995 una fuerte desaceleración que llevó al país a registrar incluso tasas negativas y perder lo logrado a principios de los noventa.
En contraste con la poca atención prestada al progreso tecnológico en Colombia, en Europa y Estados Unidos se generó una abundante literatura para tratar de explicar el papel de los avances tecnológicos en el aumento o disminución del desempleo, para lo cual se utilizaron los modelos de búsqueda como principal instrumento.
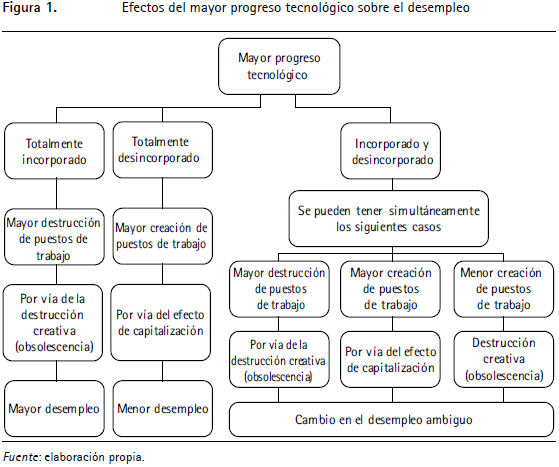
De esta literatura (descrita con mayor detalle en la siguiente sección) se desprende que la incidencia del progreso tecnológico en el desempleo depende de cómo las firmas asumen la llegada de las nuevas tecnologías. En otras palabras, depende de si el progreso tecnológico es incorporado en el puesto de trabajo y este se destruye con un consecuente despido del trabajador, o si el progreso tecnológico es desincorporado y la empresa puede actualizar el puesto de trabajo con las mejoras tecnológicas y mantener al mismo trabajador. Por ejemplo, se entiende como progreso tecnológico incorporado en el puesto de trabajo cuando una firma compra un nuevo software contable pero el trabajador que usaba el programa anterior no puede aprender a usarlo y, por lo tanto, debe ser despedido. Pero si lo aprende a manejar y conserva su puesto de trabajo, el progreso tecnológico es desincorporado, es decir, todas las firmas se pueden beneficiar de los avances tecnológicos sin necesidad de destruir los puestos obsoletos y crear nuevos.
Cuando el progreso tecnológico es incorporado, hay un efecto denominado de destrucción creativa: una aceleración del progreso tecnológico conduce a una mayor obsolescencia y, con ello, a una mayor destrucción de puestos de trabajo, lo que incrementa el desempleo. Pero si el progreso tecnológico es desincorporado, actúa el denominado efecto de capitalización, por el cual disminuye el desempleo. La posibilidad de actualización tecnológica sin necesidad de destruir los puestos de trabajo incrementa los retornos presentes y futuros de tales puestos, lo que incentiva una mayor creación de puestos de trabajo por parte de las firmas y redunda en una disminución del desempleo. No obstante, el efecto sobre el desempleo puede ser ambiguo cuando el progreso tecnológico se incorpora y desincorpora simultáneamente. El resultado depende del efecto que domine.
El propósito de este artículo es determinar cuál pudo haber sido el papel del progreso tecnológico en los resultados del mercado laboral colombiano en cuanto a desempleo, durante la década de los noventa. En particular, se quiere establecer qué tipo de progreso tecnológico y cuál de sus efectos es compatible con la evolución del desempleo, para determinar si la desaceleración del progreso tecnológico en la segunda mitad de la década explica el incremento del desempleo en Colombia en el periodo 1996-2000. Para lograr esto, se utiliza el modelo de Pissarides y Vallanti (2007). Este es un modelo con crecimiento económico y fricciones en el mercado laboral, que permite ver el impacto del progreso tecnológico, medido como el crecimiento de la PTF, sobre el desempleo.
De acuerdo con los resultados obtenidos, para que el menor progreso tecnológico haya resultado en un mayor desempleo durante la segunda mitad de la década de los noventa, el efecto de capitalización tuvo que haber dominado las otras fuerzas que pudieron generarse por una menor obsolescencia, de lo contrario se habría esperado una disminución del desempleo. Este trabajo muestra que aun en el caso extremo en que todo el progreso tecnológico hubiera sido desincorporado y solo hubiera operado el efecto de capitalización, la desaceleración de la PTF observada durante el periodo no logra explicar los incrementos en el desempleo, lo que indica que debieron ser otros factores diferentes al progreso tecnológico los que explicarían este fenómeno, entre ellos, la pérdida de eficiencia del mercado laboral para generar encuentros entre vacantes y desempleados, otras variables de política laboral y el aumento de la población económicamente activa (PEA).
El artículo está estructurado de la siguiente forma: en la primera sección se presenta la revisión de literatura relevante, con la cual se contextualiza el estudio. La segunda sección muestra algunos hechos estilizados de la tasa de desempleo y el progreso tecnológico, medido como el crecimiento de la PTF, para Colombia durante el periodo de estudio. La tercera sección describe las principales características del modelo de Pissarides y Vallanti (2007), el utilizado para realizar el análisis cuantitativo del estudio. En la cuarta sección se realiza la calibración del modelo, los ejercicios de simulación y se presentan los resultados. Las conclusiones del estudio se encuentran en la quinta sección.
I. Revisión de literatura
Determinar cuál es el efecto del progreso tecnológico sobre el desempleo es una pregunta clásica en economía, que ha sido el objeto de una extensa literatura. Como lo afirman Hornstein, Krusell y Violante (2005), esta es una pregunta clave en el análisis macroeconómico del mercado laboral, que varias aproximaciones teóricas han buscado resolver. En general, el modelo de equilibrio parcial de búsqueda3 de Diamond, Mortensen y Pissarides (DMP) y el progreso tecnológico exógeno4 bajo un enfoque de demanda por trabajo se han convertido en el marco teórico estándar para analizar las conexiones entre el progreso tecnológico y el desempleo.
Los resultados teóricos sugieren que un incremento del progreso tecnológico puede aumentar o disminuir el desempleo, dependiendo de si ante la llegada de nuevas tecnologías una firma tiene que destruir el puesto de trabajo y despedir al trabajador o puede actualizar el puesto y mantener al trabajador. En otras palabras, depende de si el progreso tecnológico es incorporado o desincorporado en los puestos de trabajo. El primer caso desarrollado por Aghion y Howitt (1994) formaliza el concepto de destrucción creativa de Schumpeter. Según este mecanismo, ante un mayor progreso tecnológico las firmas deben destruir los viejos puestos de trabajo y abrir nuevos puestos para poder adoptar las nuevas tecnologías. Así, una aceleración del progreso tecnológico genera una mayor obsolescencia (menor duración de los puestos de trabajo), que conduce a mayor desempleo.
En contraste, Pissarides (2000) encuentra que si las empresas pueden actualizar los puestos de trabajo existentes y no deben destruirlos cuando llegan las nuevas tecnologías, entonces los aumentos de productividad disminuyen el desempleo. Esto se conoce como el "efecto de capitalización": un aumento en el progreso tecnológico incrementa la productividad de todos los puestos de trabajo (existentes y nuevos) y con ello sus retornos presentes y futuros, lo cual incentiva a las firmas a una mayor creación de puestos de trabajo, lo que a su vez disminuye el desempleo.
Un caso intermedio entre estos dos mecanismos es el discutido en Mortensen y Pissarides (1998), quienes afirman que el efecto del progreso tecnológico sobre el desempleo es ambiguo y depende del costo de actualizar las viejas tecnologías. Si adoptar una nueva tecnología mediante la actualización es más costoso que crear un nuevo puesto de trabajo, la firma prefiere destruir el puesto de trabajo existente, lo que aumenta los niveles de desempleo. En cambio, si los costos de actualización son lo suficientemente bajos, la firma se inclinará por renovar de forma continua sus puestos de trabajo, con lo cual disminuye el desempleo.
Esto implica que el progreso tecnológico puede ser a la vez incorporado y desincorporado y el cambio en el desempleo dependerá de cuál efecto domine: destrucción creativa o capitalización. En este caso, la destrucción creativa también influye en la creación de trabajo y con ello en el efecto de capitalización. La reducción en la duración de los puestos de trabajo por una mayor obsolescencia disminuye la fuerza del efecto de capitalización, pues es menor el horizonte de tiempo durante el cual las firmas maximizan los beneficios del puesto de trabajo (véase figura 1).
Adicional a estos efectos, en la literatura también se menciona de manera repetida la sustitución de mano de obra por maquinaria, dados los mayores avances tecnológicos que vienen incorporados en las nuevas máquinas (Bassanini y Manfredi, 2012). En estos casos el cambio tecnológico se puede interpretar como una caída en el precio del capital por unidad de eficiencia, lo que abarata el capital en relación con el trabajo. Si el trabajo y el capital son sustitutos, la demanda por trabajo puede reducirse y con ello los salarios sí son perfectamente flexibles. Cuando los salarios no son flexibles, porque son negociados o porque existe salario mínimo, la menor demanda se puede traducir en un mayor desempleo. No obstante, Gutiérrez y Lesmes (2012) encuentran que este efecto parece ser solo de corto plazo, porque en el largo plazo el abaratamiento del capital por unidad de eficiencia, con respecto a los salarios, incrementa la rentabilidad futura de los puestos de trabajo y genera una mayor creación de empleo en el estado estacionario.
Aunque desde el punto de vista teórico parecen estar claros los resultados de estos efectos, a nivel empírico no lo son tanto y dependen mucho de las características de la economía en estudio. Por consiguiente, aún es una pregunta abierta la relación entre progreso tecnológico y desempleo a nivel agregado desde el punto de vista empírico.
Para el caso de los Estados Unidos y Europa, son varios los estudios que se han realizado para responder esta pregunta, cuyo principal instrumento teórico han sido los modelos de búsqueda, y que han establecido cuantitativamente la importancia de los efectos de capitalización y de destrucción creativa (Hornstein, Krusell y Violante, 2005, 2007; Pissarides y Vallanti, 2007; Prat, 2007). Sin embargo, en Colombia son muy pocos los trabajos que han analizado el impacto del progreso tecnológico sobre el desempleo y la mayoría se han concentrado en analizar la relación entre progreso tecnológico y empleo, principalmente a nivel de la industria manufacturera (Eslava, Haltiwanger, Kugler y Kugler, 2005; Rhenals y Bastidas, 2007).
Los modelos de búsqueda, a pesar de su popularidad para estudiar el tema en otras partes del mundo, no han sido utilizados para ello en Colombia. Echavarría et al. (2011) recurren a un modelo de fijación de precios (PS) y salarios (WS), empleando una metodología VAR-X estructural, y el estudio de González, Ocampo, Rodríguez y Rodríguez (2011), uno de los primeros en incorporar un mercado laboral con fricciones (modelo de búsqueda), lo hace en el marco de un modelo de equilibrio general dinámico y estocástico (DSGE) y para entender la relación entre el crecimiento del producto y el empleo.
Entonces, este artículo aporta en varios frentes a la literatura existente. Es uno de los primeros trabajos en utilizar modelos de equilibrio parcial de búsqueda y fricciones para estudiar la relación entre el progreso tecnológico y el desempleo en Colombia. Segundo, los trabajos existentes para el país tampoco ofrecen una explicación teórica clara de por qué el cambio tecnológico puede disminuir o aumentar el desempleo. Este trabajo es explícito en este aspecto y distingue con claridad el efecto dominante (de capitalización, destrucción creativa o los dos) en la relación entre progreso tecnológico y desempleo. Además, establece la importancia cuantitativa de estos efectos para explicar los resultados del mercado laboral colombiano en cuanto al desempleo, durante la segunda mitad de la década de los noventa.
II. Hechos estilizados
A. Tasa de desempleo
El gráfico 1 ilustra la evolución de la tasa de desempleo en las siete grandes ciudades de Colombia5 para el periodo 1991-2000. Como se puede observar, hasta mediados de la década de los noventa la tasa de desempleo estuvo entre 8% y 10%. Sin embargo, una vez pasado este periodo caracterizado por grandes cambios en el comercio internacional, la inversión extranjera directa y el régimen de la tasa de cambio (Gutiérrez, 2012), la tasa de desempleo alcanza el 20% en los años 1999 y 2000, una de las más altas de Latinoamérica durante los años noventa (Sánchez et al., 2009).
B. Progreso tecnológico: crecimiento de la PTF
Aunque en la literatura existen varias formas de medición, por lo general el progreso tecnológico se mide como incrementos en la PTF, que es la variación porcentual del producto una vez descontada la variación porcentual de los factores de producción. Los incrementos en la PTF indican los aumentos en productividad por las mejores aplicaciones de la fuerza laboral y los mayores avances tecnológicos (Clavijo, 1990).
Existen varios ejercicios de contabilidad del crecimiento para Colombia durante la década de los noventa, con resultados contradictorios6. Para Clavijo (2003), durante la década de los noventa se experimentaron mejoras importantes en la productividad, pero estas no fueron suficientes para superar las tasas negativas registradas en la llamada "década perdida" de los ochenta. No obstante, si se hacen ajustes por utilización de los factores de producción (trabajo y capital), el crecimiento de la PTF en los años noventa sí fue positivo. Según Rodríguez, Perilla y Reyes (2004), que estiman el crecimiento de la PTF ajustada por utilización del capital, el crecimiento promedio de la PTF durante los años noventa fue de 0,03%. Para Loayza, Fajnzylber y Calderón (2002), que ajustan por trabajo y capital, el crecimiento de la PTF fue de 0,51%.
En el gráfico 2 se puede observar que este mayor progreso tecnológico de los años noventa se experimentó principalmente en la primera mitad de la década, cuando se registraron incrementos importantes como resultado del proceso de apertura económica (Clavijo, 2003; Echavarría, Arbeláez y Rosales, 2006). Entre los años 1996 y 2000, el país cayó en una profunda crisis económica y se presentó una fuerte desaceleración de la PTF, que mitigó los avances de la primera mitad de la década y generó de nuevo tasas de crecimiento negativas, como en los años ochenta7.
C. Progreso tecnológico y desempleo
Analizando de manera conjunta la evolución del desempleo y el crecimiento de la PTF para la década de los noventa en Colombia, puede observarse que existió una relación inversa en la mayor parte del periodo (gráfico 2). En la primera mitad de la década, cuando la PTF se incrementó, la tasa de desempleo registró disminuciones y a partir de 1995, cuando la PTF mostró una desaceleración, la tasa de desempleo empezó su senda creciente.
Entonces, ¿la desaceleración del crecimiento de la PTF en la segunda mitad de la década de los noventa puede explicar los fuertes incrementos del desempleo que registró Colombia en el periodo 1996-2000? Si esto es así, necesariamente debió existir un cambio tecnológico desincorporado y un dominio del efecto de capitalización sobre los otros posibles efectos por vía de la obsolescencia. Por consiguiente, menores tasas de crecimiento de la PTF debieron desmotivar la creación de puestos de trabajo, por la menor rentabilidad esperada, y aumentó el desempleo.
III. Modelo8
El modelo teórico que se utiliza para analizar la relación entre el progreso tecnológico y el desempleo en Colombia es el modelo de búsqueda de Pissarides y Vallanti. Este es un modelo con crecimiento económico y un mercado laboral con fricciones9, en donde las nuevas tecnologías pueden ser tanto desincorporadas como incorporadas en los puestos de trabajo. Además, es de equilibrio parcial y analiza el impacto del progreso tecnológico sobre el desempleo en estado estacionario.
De forma concreta, en el modelo se asume que hay dos tipos de tecnología. Una, denotada por A1, la cual puede ser aplicada tanto en los trabajos existentes como en los nuevos trabajos, y la otra, denotada por A2, que puede usarse solo en nuevos puestos de trabajo y requiere la destrucción de los puestos de trabajo existentes para poder ser apropiada. Las tasas de crecimiento de ambas tasas son, respectivamente: λa y (1-λ)a, con 0 ≤ λ ≤ 1, donde λ y a son parámetros. El parámetro l mide la proporción del progreso tecnológico total (a) que es desincorporado y no requiere la destrucción de puestos de trabajo. Entonces, si λ = 0, el progreso tecnológico es totalmente incorporado, pero si λ = 1, toda la tecnología es desincorporada. El parámetro a, que es la tasa total de crecimiento de la tecnología, se mide como el crecimiento de la PTF.
En este modelo, a diferencia de otros (como el de Mortensen y Pissarides, 1998), se introduce explícitamente una función de producción, la cual es de tipo Cobb-Douglas, donde los dos tipos de progreso tecnológico introducidos son aumentadores de trabajo10. La producción por trabajador11 se denota por f (.,.), donde el primer argumento de f (.,.) denota el tiempo de creación del puesto de trabajo y el segundo, el tiempo actual. Si el puesto de trabajo fue creado en el momento τ, el producto por trabajador en el tiempo t > τ es:
donde 0 < a ≤ 1 y k (.,.) es el stock de capital por trabajador.
La ecuación (1) muestra que un puesto de trabajo creado en el momento t solo puede beneficiarse de las mejoras tecnológicas desincorporadas A1(t), que son actualizadas con el paso del tiempo (efecto de capitalización), pero no de la tecnología que requiere incorporación A2(τ); para ello, el puesto de trabajo tendría que ser destruido y crearse uno nuevo en su lugar (destrucción creativa). En cambio, los nuevos puestos de trabajos, creados en cada momento t, sí pueden beneficiarse de todo el progreso tecnológico (desincorporado e incorporado), siendo de esta forma más avanzados tecnológicamente que los puestos de trabajo existentes.
Esto implica que mientras los nuevos puestos de trabajo se mantienen creciendo a una tasa a en la frontera tecnológica, los puestos de trabajo existentes crecen a una tasa más baja λa y solo regresan a la frontera tecnológica por un proceso de destrucción creativa12. Esta especificación permite establecer la importancia cuantitativa de los efectos de capitalización y destrucción creativa en la evolución del desempleo.
A. Salario
El salario (w) se determina de forma conjunta por la empresa y el trabajador después de una negociación. Se asume que el salario resultante es una regla de partición del excedente generado por el puesto de trabajo ocupado, que es explicada a través de un juego no cooperativo, cuya solución es de tipo Nash13. La ecuación del salario, para un puesto de trabajo creado en el tiempo t, se puede escribir como un promedio ponderado del salario de reserva14 (ω) que crece a la tasa a y del producto marginal del factor trabajo (φ) que crece a la tasa λa . β  [0,1) refleja el poder de negociación del trabajador en el proceso de negociación y actúa como ponderador.
[0,1) refleja el poder de negociación del trabajador en el proceso de negociación y actúa como ponderador.
donde:
donde b es el ingreso del desempleado que crece a una tasa a y, por lo tanto, el salario de reserva (ω) también crece a una tasa a, un supuesto necesario para garantizar un estado estacionario; θ ≥ 0 es la medida de la estrechez del mercado laboral y se define como el cociente entre vacantes y trabajadores desempleados; m(θ) es la tasa a la cual una nueva oferta de trabajo llega a un trabajador desempleado y J es el valor presente neto del valor (beneficios) de un puesto de trabajo.
Entonces, en los puestos de trabajo existentes aunque la tecnología crece a una tasa λa, los salarios crecen a una mayor tasa, entre λa y a, dada su dependencia del salario de reserva (ω), que crece proporcionalmente a la productividad total (a).
B. Creación y destrucción de los puestos de trabajo
En el modelo, la destrucción de un puesto de trabajo puede darse por dos razones: la llegada de un choque exógeno a los puestos ocupados que ocurre en una tasa s o por motivos de obsolescencia, que toma lugar T periodos después de su creación.
El tiempo de obsolescencia T lo determinan cada una de las firmas y es aquel que maximiza los beneficios generados por un puesto de trabajo (J ). Viene dado por:
Entonces, un puesto de trabajo es destruido cuando el salario de reserva (ω) llega a ser igual al producto marginal del factor trabajo (φ). Esto lleva a que el salario sea igual al salario de reserva (véase ecuación 2) y que el puesto de trabajo no sea viable, pues el salario de reserva sigue creciendo a una tasa más rápida (a) que aquella a la que crece el producto marginal del factor trabajo (λa).
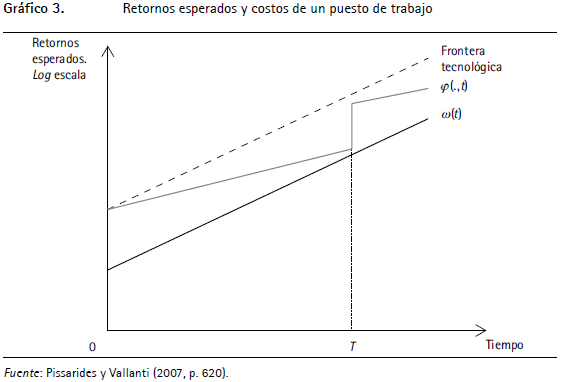
Lo anterior se puede observar de forma más clara en el gráfico 3. El eje horizontal muestra el tiempo y el eje vertical mide el producto marginal del factor trabajo (φ) y el salario de reserva (ω). La línea discontinua muestra la senda del producto marginal si el trabajo permaneciera en la frontera tecnológica, la cual crece a la tasa a . La línea paralela continua que se encuentra debajo muestra el salario de reserva (ω) que también crece a una tasa a . Entonces, un puesto de trabajo es creado en la frontera tecnológica en el momento 0 y con el paso del tiempo el producto marginal del factor trabajo (φ) crece a una tasa más baja (λa), lo cual se muestra por la línea gris. Eventualmente, llega un momento T en el que el producto marginal del puesto de trabajo es menor al salario de reserva (cuando el producto marginal del factor trabajo, φ, golpea la línea del salario de reserva, ω) y el puesto de trabajo es destruido. La firma u otra firma crean otro puesto de trabajo en su lugar con el producto marginal (φ) en la frontera tecnológica.
Siguiendo con la ecuación (4) y el gráfico 3, si todo el progreso tecnológico es desincorporado, (λ = 1), la firma nunca destruirá el puesto de trabajo por obsolescencia, pues el salario de reserva y el producto marginal del factor trabajo crecerían a la misma tasa. En este caso, un puesto de trabajo solo se destruiría por causa del proceso exógeno de separación (s). Pero si λ < 1, el mayor progreso tecnológico conduce a una mayor destrucción del puesto de trabajo ( T /
T /  a < 0), pues el salario de reserva crece a una mayor tasa que el producto marginal del factor trabajo.
a < 0), pues el salario de reserva crece a una mayor tasa que el producto marginal del factor trabajo.
La creación de un puesto de trabajo, que se lleva a cabo cuando una firma y un trabajador se encuentran y acuerdan un salario, viene en parte determinada por los beneficios que percibe la firma tanto por crear una vacante como por participar en un proceso de contratación. Esto define la curva de creación de trabajo, que viene dada por:
donde c es el costo de crear un puesto vacante15 en el periodo t y
Para obtener el efecto del progreso tecnológico en la creación de puestos de trabajo, para un nivel dado de desempleo, se deriva la ecuación (5) con respecto a a y se obtiene:
donde η  (0,1) es la elasticidad de m(θ). El coeficiente que acompaña a
(0,1) es la elasticidad de m(θ). El coeficiente que acompaña a  θ /
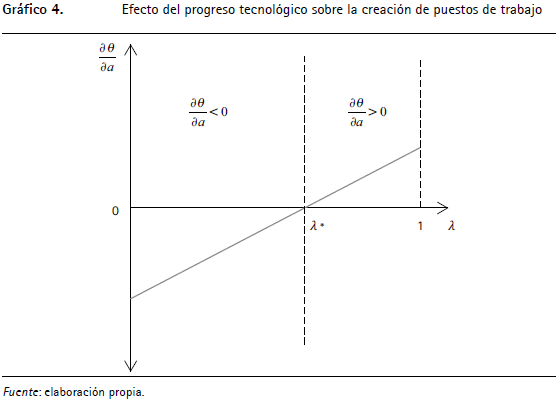
θ /  a es positivo, pero el lado derecho puede ser positivo o negativo y depende del valor que tome l. Si λ = 0, es negativo, y si λ = 1, es positivo. Por lo tanto, hay un único valor de λ, llamado λ*, tal que en valores de λ < λ*, un mayor progreso tecnológico reduce θ y, en valores de λ > λ*, un mayor progreso tecnológico aumenta θ; en otras palabras, dependiendo de si λ es mayor o menor que λ*, el progreso tecnológico aumenta o disminuye la creación de puestos de trabajo. En el caso en que λ = λ*, el progreso tecnológico no tiene ningún efecto sobre θ. Esto se puede observar claramente en el gráfico 4.
a es positivo, pero el lado derecho puede ser positivo o negativo y depende del valor que tome l. Si λ = 0, es negativo, y si λ = 1, es positivo. Por lo tanto, hay un único valor de λ, llamado λ*, tal que en valores de λ < λ*, un mayor progreso tecnológico reduce θ y, en valores de λ > λ*, un mayor progreso tecnológico aumenta θ; en otras palabras, dependiendo de si λ es mayor o menor que λ*, el progreso tecnológico aumenta o disminuye la creación de puestos de trabajo. En el caso en que λ = λ*, el progreso tecnológico no tiene ningún efecto sobre θ. Esto se puede observar claramente en el gráfico 4.
C. Tasa de desempleo de equilibrio
La tasa de desempleo de equilibrio (u) en estado estacionario es aquella donde la tasa de creación de trabajo es igual a la tasa de destrucción de puestos de trabajo. Usando las ecuaciones (6) y (5) que definen, respectivamente, las variables endógenas θ y T, se encuentra que la tasa de desempleo de equilibrio (u) puede expresarse como:
donde n es la tasa de crecimiento de la PEA.
En resumen, el modelo indica que el crecimiento del progreso tecnológico (a) incrementa la destrucción de trabajos por vía de la obsolescencia y puede incrementar o disminuir la creación de puestos de trabajo dependiendo del valor tomado por el parámetro λ (nivel de progreso tecnológico desincorporado), con lo cual se determina el efecto de a sobre el desempleo. En concreto, se tiene que existe un λ* tal que cambios en a no afectan θ, y por ende, la creación de puestos de trabajo. Entonces, para valores λ  [0,λ*]
[0,λ*] 
 < 0, a medida que a aumenta, la destrucción de puestos de trabajo aumenta y la creación de puestos de trabajo se mantiene constante o disminuye, y en este caso el impacto de a sobre el desempleo es positivo. Para valores de λ
< 0, a medida que a aumenta, la destrucción de puestos de trabajo aumenta y la creación de puestos de trabajo se mantiene constante o disminuye, y en este caso el impacto de a sobre el desempleo es positivo. Para valores de λ  (λ*,1)
(λ*,1) 
 > 0, el impacto de a sobre el desempleo puede ser positivo o negativo, dependiendo de la fuerza del efecto de destrucción creativa y el efecto de capitalización. Si λ = 1, no existiría el efecto de destrucción creativa (T = ∞) y el impacto de a sobre el desempleo sería negativo, dado que solo hay efecto de capitalización: todos los puestos de trabajo (nuevos y existentes) se benefician por igual del progreso tecnológico.
> 0, el impacto de a sobre el desempleo puede ser positivo o negativo, dependiendo de la fuerza del efecto de destrucción creativa y el efecto de capitalización. Si λ = 1, no existiría el efecto de destrucción creativa (T = ∞) y el impacto de a sobre el desempleo sería negativo, dado que solo hay efecto de capitalización: todos los puestos de trabajo (nuevos y existentes) se benefician por igual del progreso tecnológico.
IV. Calibración, simulación y resultados
Para que el progreso tecnológico haya redundado en un mayor desempleo durante la segunda mitad de la década de los noventa, el modelo indica que el efecto de capitalización tuvo que haber dominado, pues de lo contrario se habría esperado una disminución del desempleo. En efecto, una tasa de obsolescencia más baja hubiera producido una menor destrucción de puestos de trabajo (efecto de destrucción creativa) y una mayor creación de puestos de trabajo por una menor obsolescencia de estos.
Ahora, si el efecto que dominó la relación entre el progreso tecnológico y el desempleo fue el de capitalización, ¿en cuánto logra explicar este el aumento del desempleo visto en Colombia durante la segundad mitad de la década de los noventa? En otras palabras, dado el efecto sobre la creación de puestos de trabajo, ¿en cuánto fue el aumento del desempleo entre 1996-2000 por causa de la desaceleración del progreso tecnológico?
El análisis cuantitativo que se realiza a continuación busca establecer la magnitud del impacto del progreso tecnológico sobre el desempleo y responder la anterior pregunta. Para ello, se utiliza el modelo de Pissarides y Vallanti (2007) ya explicado, asumiendo que todo el progreso tecnológico fue desincorporado, es decir, λ = 1, y se recurre a un ejercicio de simulación para calcular cuál hubiera sido la tasa de desempleo para la segunda mitad de la década de los noventa si el progreso tecnológico no se hubiera desacelerado sino que hubiera seguido creciendo.
De esta forma se obtiene el máximo impacto posible del progreso tecnológico sobre el desempleo en Colombia, dado que se está asumiendo que todo el progreso tecnológico fue desincorporado y no hubo ninguna fuerza que contrarrestara el efecto de capitalización, efecto que se tradujo en una menor creación de los puestos de trabajo ante la desaceleración de la PTF. Como se verá en lo que sigue, aun en este caso extremo el cambio tecnológico explica muy poco del crecimiento en el desempleo.
A. Estrategia de calibración y resultados
1. Estrategia de calibración
Para obtener los cambios en el desempleo por variaciones en el progreso tecnológico, primero es necesario calibrar las siguientes variables endógenas y el parámetro del modelo no observables en los datos colombianos:
Las dos variables señaladas en el cuadro 1, ω y θ, se calibran a partir de las ecuaciones que definen el salario de reserva (ecuación 3) y la curva de creación de trabajo (ecuación 5), explicadas en las secciones III(A) y III(B), respectivamente. Estas ecuaciones mediante ciertas transformaciones y el supuesto de λ = 1 quedan expresadas como16:
El flujo de encuentros, m(θ), siguiendo lo encontrado en diferentes estudios empíricos (Petrongolo y Pissarides, 2001), se toma como:
de tal forma que (11) se puede expresar como:
Para calibrar el parámetro m0 se hace uso de la ecuación que define el desempleo de equilibrio (u), que con λ = 1 viene definida por:
de tal manera que se tiene un sistema de ecuaciones exactamente identificado de tres ecuaciones (10, 13 y 14) con tres incógnitas (ω, θ y m0). Aunque el producto marginal del factor trabajo (φ) también es una variable no observable, no es importante en este ejercicio de calibración17. Siguiendo a Pissarides y Vallanti (2007) para calibrar los valores no observables especificados, se reexpresan las ecuaciones en función del producto marginal del factor trabajo (φ) (véase anexo 1).
2. Parámetros observables
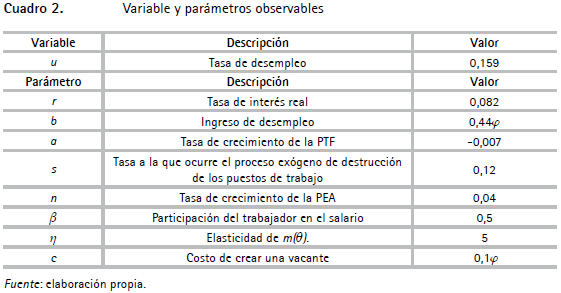
El ejercicio de calibración se realiza para el periodo 1996-2000 usando el valor anual promedio que la variable y los parámetros observables del modelo registraron durante este periodo (cuadro 2)18.
La tasa de desempleo (15,9%) es el promedio anual de la tasa de desempleo para las siete grandes ciudades de Colombia, reportada por el Departamento Administrativo Nacional de Estadística (DANE) a partir de la Encuesta Nacional de Hogares (ENH). El valor de la tasa de interés (8,2%) es el promedio anual de la tasa de captación por depósitos de término fijo (DTF), ajustado por inflación. Esta tasa es reportada por el Banco de la República y se refiere a la tasa promedio ponderada por monto de las captaciones por los certificados de depósito a término (CDT) a 90 días para los bancos, corporaciones y compañías de financiamiento comercial.
El ingreso del desempleo (b) se define en este caso como el ingreso de los trabajadores informales y, siguiendo a Pissarides y Vallanti (2007), se asume proporcional al producto marginal del trabajo (φ); el valor estimado b = 0, 44φ garantiza que en equilibrio la relación entre salario informal y salario formal sea de 52%, promedio anual observado en Colombia durante los años 1996-2000 (Mondragón-Vélez, Peña y Wills, 2010). La tasa de crecimiento de la PTF, a = -0,7%, se toma de Rodríguez et al. (2004), quienes realizan un ejercicio de contabilidad de crecimiento asumiendo una función de producción Cobb-Douglas y ajustan por uso del capital19.
La tasa a la que ocurre el proceso exógeno de destrucción de los puestos de trabajo, s = 12%, es la tasa promedio de destrucción bruta de puestos de trabajo en el sector manufacturero (Wengel, 2006)20. En cuanto a la tasa de crecimiento de la PEA, n = 4,0%, se obtiene a partir de la PEA reportada por el DANE para las siete grandes ciudades de Colombia, usando como fuente la ENH.
Los parámetros restantes se fijan a partir de valores predeterminados. La participación de los trabajadores en el salario, β = 0,5, es el valor estándar establecido en la literatura (Pissarides, 2000). En cuanto a la elasticidad de m(θ), siguiendo los resultados obtenidos por la mayoría de estudios que han estimado la función de encuentros, se establece como η = 0,5 (Petrongolo y Pissarides, 2001). Para los costos de crear una vacante (c), se toma el valor de Pissarides y Vallanti (2007), quienes asumen que son aproximadamente un mes de salario. Cuando este costo se hace proporcional al producto marginal del trabajo (φ), corresponde a c = 0,1φ. Más adelante se realizan ejercicios de robustez sobre estos supuestos.
3. Resultados
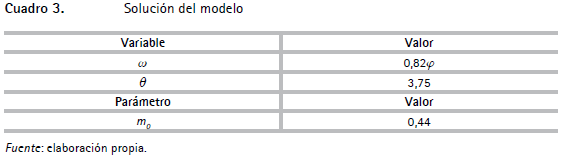
Del respectivo ejercicio de calibración se obtienen las siguientes soluciones para las variables y el parámetro desconocidos del modelo:
El valor del salario de reserva (ω) es levemente menor al de Pissarides y Vallanti (0,94 φ) y es consistente con la teoría económica que sugiere que este debe ser menor a la productividad del trabajo. En cuanto a θ, que indica la estrechez del mercado laboral y se interpreta como el cociente entre vacantes y desempleados, un valor de θ = 3,75 indica que durante este periodo en promedio existieron cuatro vacantes por cada trabajador desempleado, valor que junto a un m0 = 0,44 muestra la ineficiencia del mercado laboral para generar los encuentros entre vacantes y desempleados21.
Estos valores de θ y m0 implican una duración del desempleo22 consistente con lo observado. Con θ = 3,75 y m0 = 0,44 la duración promedio del desempleo para el periodo 1996-2000 fue de 62 semanas, valor que se encuentra entre el rango de tiempo que duraron las personas desempleadas en buscar un nuevo empleo, el cual estuvo entre 28 y 77 semanas (Núñez y Bernal, 1997).
Después de un ejercicio de robustez se encuentra que ω resulta robusto ante variaciones razonables de los parámetros asumidos (β, η y c). En cuanto a θ y m0, el ajuste que estos arrojan para dar un nivel constante de encuentros23 sugiere una gran sensibilidad ante cambios en los parámetros (β, η y c). Esta sensibilidad parece indicar que el modelo no es efectivo en identificar por separado los efectos del cambio tecnológico (y otras variables exógenas) sobre la demanda de trabajo, por un lado, y la eficiencia del mercado, por el otro. Por esta razón se opta por verificar la robustez del modelo mediante un indicador integrado de ambas variables (If ). En efecto, si se realiza el análisis de robustez de θ y m0 de forma conjunta a través del indicador (If ), definido por:
se encuentra que en conjunto el valor calibrado de If también es robusto ante cambios de los parámetros asumidos (β, η y c). La utilización de este indicador muestra las combinaciones posibles de θ y m0 consistentes con un nivel fijo de encuentros (m) y es un indicador resumen de todas las variables de política que afectan la creación de vacantes (por ejemplo, la demanda de trabajo) y la eficiencia del mercado. Los resultados se muestran en el cuadro 4.
B. Simulación
1. Estrategia de simulación
Una vez calibradas las variables y parámetros no observables, mediante la ecuación (14) se realiza un ejercicio de simulación para determinar los cambios en la tasa de desempleo ante cambios en el progreso tecnológico. Se asume que λ = 1, de tal forma que los efectos del progreso tecnológico sobre u son por medio de θ, es decir, solo desde la creación del puesto de trabajo y donde  θ /
θ /  a > 0. En concreto, se establece cuál hubiera sido la tasa de desempleo para la segunda mitad de la década de los noventa si el progreso tecnológico no se hubiera desacelerado sino que hubiera seguido creciendo a una tasa del 0,8%, que fue la tasa promedio de crecimiento de la PTF durante el periodo 1991-1995, en el caso extremo donde todo el progreso fuera desincorporado y solo actuara el efecto de capitalización.
a > 0. En concreto, se establece cuál hubiera sido la tasa de desempleo para la segunda mitad de la década de los noventa si el progreso tecnológico no se hubiera desacelerado sino que hubiera seguido creciendo a una tasa del 0,8%, que fue la tasa promedio de crecimiento de la PTF durante el periodo 1991-1995, en el caso extremo donde todo el progreso fuera desincorporado y solo actuara el efecto de capitalización.
2. Resultados simulación
Como se observa en el cuadro 5, si en el periodo 1996-2000 no se hubiera presentado un crecimiento promedio de la PTF de -0,7% sino de 0,8%, la tasa de desempleo promedio habría sido de 15,7%, solo 0,2 puntos porcentuales menos de la registrada para el periodo de estudio (15,9%), es decir que aunque no se hubiera presentado esta disminución, la tasa de desempleo hubiera sido casi igual de alta. En otras palabras, una disminución del crecimiento de la PTF en 1,5 puntos porcentuales solo aumentaría la tasa de desempleo en 0,2 puntos porcentuales.
Entonces, de los 7,3 puntos porcentuales que aumentó la tasa de desempleo entre la primera y la segunda mitad de la década de los noventa, solo 0,2 (2,7%) de estos incrementos se podrían explicar por la desaceleración de la PTF. Estos resultados indican que, aun en el caso extremo en que ninguna fuerza estuviera contrarrestando el efecto de capitalización (λ = 1), la relación negativa entre progreso tecnológico y desempleo que existió en la segunda mitad de la década no fue lo suficientemente fuerte para explicar los aumentos sostenidos en la tasa de desempleo en el periodo 1996-2000.
3. Consideraciones adicionales
Entre 1998-2000 se registró una de las crisis económicas más profundas en la historia del país y, en consecuencia, variables como el desempleo tuvieron cambios abruptos en su comportamiento. Modelos simplificados como el calibrado en este trabajo con frecuencia se quedan cortos para reproducir los hechos registrados en periodos de fluctuaciones fuertes de la economía. Esto podría explicar por qué el modelo anterior calibrado para el periodo 1996-2000 no logró reproducir los drásticos cambios en el desempleo. Sin embargo, al realizar de nuevo el ejercicio de simulación pero solo para el periodo 1996-1997 -en el que no se presentó una crisis económica-, se encuentra que una vez más los cambios en la tasa de crecimiento de la PTF no generan cambios importantes en la tasa de desempleo. De acuerdo con los resultados del modelo (véase cuadro 6)24, si en el periodo 1996-1997 no se hubiera presentado un crecimiento promedio de la PTF de 1,6% sino de 0,8%, la tasa de desempleo promedio habría sido aproximadamente la misma: 12,2%, solo 0,1 punto porcentual más que la observada para este periodo.
Por otra parte, una de las principales desventajas del modelo de Pissarides y Vallanti (reconocida por los propios autores en su trabajo) es la necesidad de que haya valores pequeños de r + s o grandes cambios en a para que el efecto de capitalización sea fuerte y, por ende, el progreso tecnológico tenga un gran impacto sobre el desempleo. Esto porque la tasa que utilizan las firmas para descontar los beneficios de un puesto de trabajo es r + s - a. Para ver si valores más pequeños de r + s o más grandes de a mejoran los resultados antes analizados para el periodo 1996-2000, se realiza nuevamente el ejercicio de simulación con r + s = 0,1, r + s = 0,05 y a = 0,1. Los resultados se muestran en el cuadro 7.
Cuando se utilizan valores más pequeños de r + s los resultados no son muy distintos de los obtenidos anteriormente. En el caso de tener un r + s = 0,05, el más bajo de los analizados, la tasa de desempleo solo hubiera aumentado en 0,4 puntos porcentuales por una disminución del crecimiento de la PTF, 0,2 puntos porcentuales más de lo que se obtuvo con la tasa de descuento inicial.
Cuando se utiliza un a = 0,1, la tasa de desempleo solo aumentaría en 1,3 puntos porcentuales. Es decir, aun si el progreso tecnológico hubiera sido del 10% promedio anual, un valor alto según estándares internacionales, no se habría logrado explicar la tasa de desempleo en Colombia en este periodo de estudio.
Estos resultados sugieren que o bien el modelo requiere progresos tecnológicos demasiado grandes para tener un efecto sobre el desempleo o bien los parámetros calibrados para el caso colombiano implican un mercado laboral poco sensible al progreso tecnológico.
La calibración del modelo de Pissarides y Vallanti para los Estados Unidos arroja resultados parecidos, lo que sugiere que quizá es conveniente revisar si otros modelos arrojan una mayor sensibilidad del desempleo ante el progreso tecnológico, algo que va más allá de este trabajo. En lo que sigue, en cambio, se explora qué otros factores podrían explicar el incremento del desempleo para el periodo 1996-2000, dado el modelo usado en este trabajo.
4. ¿Fueron otros factores?
Los anteriores resultados muestran que no fue significativo el papel del progreso tecnológico en la explicación de los incrementos en el desempleo durante la segunda década de los noventa, lo que indica que pudieron ser otros los factores que influenciaron los incrementos del desempleo en este periodo.
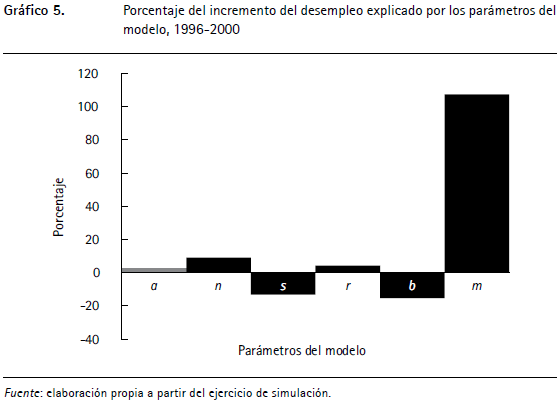
Para identificar las posibles causas de estos incrementos en el desempleo, diferentes al progreso tecnológico, se realiza de nuevo el ejercicio de simulación, pero con las variaciones de los parámetros observables del modelo. En concreto, se calcula cuál hubiera sido la tasa de desempleo si la tasa de crecimiento de la PEA (n), la tasa de interés (r), la tasa a la que ocurre el proceso exógeno de destrucción de los puestos de trabajo (s), el ingreso del desempleo (b) y la constante de la función de encuentros (m0)25 no hubieran cambiado sino que se hubieran mantenido en los niveles de los primeros años de la década de los noventa26. Los resultados aparecen en el cuadro 8.
Los resultados de este ejercicio indican que los cambios en el desempleo pueden ser explicados en su totalidad (107,4%) por los aumentos en la ineficiencia del mercado laboral, los cuales se concretizan en la reducción de la constante de la función de encuentros (m0) de 0,86 a 0,44 entre los dos periodos. Otro factor que parece explicar una parte importante de los incrementos en el desempleo (9,2%) es el aumento de la participación laboral que se presentó a partir de 1996. El aumento de la tasa de interés (r) explica una parte no muy importante de estos incrementos (4,2%). La reducción de la tasa de destrucción de puestos de trabajo (s) y la disminución de los ingresos de los informales con respecto a los formales (b) posiblemente generaron un efecto contrario y llevaron a que los aumentos en la tasa de desempleo no fueran mayores (gráfico 5).
Es importante aclarar que si bien en el modelo, teóricamente, m0 capta la eficiencia del mercado laboral, en la parametrización realizada en este trabajo no se tienen en cuenta otras variables de política, como el salario mínimo y los costos no salariales. Por ende, m0 puede estar captando los cambios no despreciables que se dieron durante la década de los noventa en estas otras variables. Por ejemplo, el salario mínimo real entre 1995 y 1999 creció cerca de 17%, lo que representó en este último año casi el 75% del PIB per cápita del país, el más alto de Latinoamérica en este periodo (véanse Echavarría et al., 2011; Sánchez et al., 2009). En cuanto a los costos no salariales, como resultado de la ley 100 de 1993, los cambios se dieron principalmente en los aportes a salud y pensión. Entre 1994 y 1996, los aportes a salud pasaron del 7% al 12% del salario y los aportes a pensiones del 11,5% al 13,5%. Con estos incrementos los costos no salariales pasaron a representar para los empleadores el 52% del salario a finales de la década de los noventa (Ramírez y Núñez, 2000; Sánchez et al., 2009).
A partir de los resultados de estos ejercicios de simulación, se puede concluir que los incrementos de la tasa de desempleo en la segunda mitad de la década de los noventa se debieron a otros factores diferentes a la desaceleración del progreso tecnológico. El aumento de la ineficiencia del mercado laboral para generar los encuentros entre vacantes y trabajadores desempleados, otras políticas laborales y el incremento de la participación laboral parecen ser los factores más importantes.
V. Conclusiones
El progreso tecnológico, medido como el crecimiento de la PTF, en Colombia durante la década de los noventa estuvo acompañado de un aumento del desempleo. De acuerdo con los resultados teóricos encontrados en la literatura sobre la relación entre el progreso tecnológico y el desempleo, este hecho indicaría que el efecto de capitalización debió dominar las otras fuerzas que pudieron generarse por menor obsolescencia. El presente artículo muestra que aun en el caso extremo en que todo el progreso tecnológico se hubiera desincorporado y solo hubiera operado el efecto de capitalización, la desaceleración de la PTF observada durante el periodo no logra explicar los incrementos en el desempleo. En otras palabras, si se permitiera la existencia del progreso tecnológico incorporado y la de efectos de destrucción creativa, que contrarrestarían la menor creación de empleo, la capacidad del progreso tecnológico para explicar el incremento en el desempleo sería aún menor.
Asimismo, que solo 0,2 puntos porcentuales del incremento de la tasa de desempleo entre la primera y la segunda mitad de la década de los noventa pueda explicarse por la desaceleración de la PTF implica que debieron ser otros los factores que determinaron tal aumento en la tasa de desempleo. Estos factores parecen ser la pérdida de eficiencia del mercado laboral para generar encuentros entre vacantes y desempleados, otras variables de política laboral y el aumento de la PEA.
Ahora bien, como se discutió, el modelo de Pissarides y Vallanti presenta limitaciones en su capacidad para explicar la relación progreso tecnológicodesempleo, en particular el modelo parece poco sensible a cambios en el progreso tecnológico. Además, el modelo no considera otros canales a través de los cuales el progreso tecnológico puede afectar el desempleo. En concreto, un factor importante que queda pendiente por analizar es el progreso tecnológico incorporado en el capital, el cual se ha evidenciado en el mundo a través del abaratamiento del capital por unidades de eficiencia. Por lo tanto, una de las líneas de investigación para Colombia debería encaminarse a la exploración de estas áreas.
En otros trabajos, mediante la aplicación cuantitativa del modelo desarrollado por Hornstein et al. (2005) se explora el impacto de este tipo de progreso tecnológico y los primeros resultados indican que la contribución de este en el incremento del desempleo de este periodo no es superior al 1% (véase Lesmes, 2012).
Además y como se mencionó en la revisión de literatura, hay otros efectos que han sido menos considerados y que pueden llevar a un mayor desempleo, en particular la posible sustitución entre capital y trabajo causada por el menor precio del capital por unidad de eficiencia con respecto al salario. Los resultados encontrados hasta ahora, como los de Gutiérrez y Lesmes (2012), aún preliminares, parecen indicar que estos efectos serían solo de corto plazo.
Así las cosas, puede concluirse que el progreso tecnológico no es suficiente para explicar el aumento del desempleo en Colombia y, por lo tanto, en lugar de limitarlo debería ser impulsado. No obstante, este impulso del avance tecnológico debería estar acompañado de incrementos en los niveles de calificación de los trabajadores, que faciliten la adopción constante de tecnologías sin destruir los puestos de trabajo y, por consiguiente, favorezcan el efecto de capitalización, creador de empleo.
_____________________________
Notas al Pie
3 Los modelos de búsqueda (matching models) permiten la existencia de fricciones en el mercado laboral y con ello la existencia de desempleo involuntario. El propósito de estos modelos es señalar la naturaleza del desempleo en estado estacionario y mostrar cómo los salarios y el desempleo se determinan conjuntamente en un modelo de equilibrio parcial estándar.
4 Se asume exógeno por cuanto la tecnología aumenta sin necesidad de que la economía dedique esfuerzos o recursos para que ello suceda (Sala-i-Martin, 2000).
5 Bogotá, Medellín, Cali, Barranquilla, Bucaramanga, Manizales y Pasto. De acuerdo con Echavarría et al. (2011) aunque la tasa de desempleo para el total nacional fue un poco menor, esta tasa siguió una dinámica muy similar.
6 Estos varían en cuanto a forma funcional, método de estimación, periodo de estudio y ajustes.
7 Algunos de los ejercicios de contabilidad del crecimiento para el país indican que esta desaceleración fue tan fuerte que sobrepasó los avances de la primera mitad de la década, lo que llevó a que el promedio anual de crecimiento de la PTF de los noventa fuera menor que el registrado en los ochenta.
8 Esta sección se toma completamente de Pissarides y Vallanti (2007). El desarrollo que se presenta está enfocado en mostrar las ecuaciones clave para entender la calibración. Para ver en mayor detalle la derivación de las ecuaciones, puede revisar el respectivo documento.
9 Mercado friccional al estilo Pissarides (2000).
10 El progreso tecnológico aumenta la productividad del factor trabajo. Se podría obtener la misma producción con una cantidad menor del factor trabajo.
11 Si F = Ka (AL)1-a, la producción por trabajador (f) es:  .
.
12 Esto también implica que el stock del capital y el producto marginal del factor trabajo de los nuevos puestos de trabajo crezcan más rápido que los puestos de trabajo existentes.
13 Pissarides y Vallanti (2007) también estudian las implicaciones de otro tipo de ecuación de salario, en la cual asumen que el salario es una fracción constante del producto marginal del factor trabajo.
14 El salario de reserva debe entenderse como aquel salario mínimo a partir del cual un individuo estaría dispuesto a aceptar un empleo en vez de permanecer desempleado.
15 Estos costos también crecen a una tasa a, para garantizar la existencia del estado estacionario del modelo.
16 Para ver en mayor detalle la derivación de las ecuaciones (1) y (11), revisar el documento de Pissarides y Vallanti (2007).
17 De acuerdo con Pissarides y Vallanti (2007), el valor de φ no necesita especificarse, dado que no influencia el estado estacionario y, por ende, la calibración de las variables del modelo.
18 Es decir que todos los valores de los parámetros se toman para el periodo 1996-2000.
19 Para más detalles, véase el anexo 2.
20 Wengel (2006) determina esta tasa siguiendo a Davis y Haltiwanger (1992) y utilizando la información de la Encuesta Anual Manufacturera del DANE. Se hicieron ejercicios de robustez para el valor de este parámetro y los valores de las variables calibradas no presentan cambios significativos. Estos resultados no se muestran en el documento, pero están disponibles a solicitud del interesado.
21 De acuerdo con Cahuc y Zylberberg (2004), las mejoras en eficiencia en la función de encuentros, m(θ), vienen dadas por la multiplicación de un coeficiente, m0, positivo mayor que uno.
22 De acuerdo con el modelo, la duración del desempleo está definida por:  .
.
23 m(θ) = m0θη.
24 Los resultados de este ejercicio de calibración y robustez no se presentan en el artículo, pero están disponibles a solicitud del interesado.
25 El valor de m0 para el periodo 1991-1995 fue obtenido a partir de un ejercicio de calibración similar al realizado para el periodo 1996-2000 de la sección IV(A). Véase el anexo 3.
26 Igual que el ejercicio de simulación con progreso tecnológico, a partir de la diferencia entre la tasa de desempleo simulada y la tasa de desempleo observada en el periodo 1996-2000, se determina qué porcentaje del crecimiento de la tasa de desempleo entre la primera y la segunda mitad de la década de los noventa (7,3 puntos porcentuales) se explica por el cambio en el valor del parámetro, manteniendo el resto constante.
Referencias
1. AGHION, P. y HOWITT, P. (1994). "Growth and unemployment", The Review Economic Studies, 61(3):477-494. [ Links ]
2. BARRIOS, A., HENAO, M. L., POSADA, C. E., VALDERRAMA, F. M. y VÁSQUEZ, D. M. (1993). "Empleo y capital en Colombia: nuevas estimaciones (1950-1992) (Archivo de Macroeconomía 15)". Departamento Nacional de Planeación. [ Links ]
3. BASSANINI, A. y MANFREDI, T. (2012). Capital's grabbing hand? A crosscountry/cross-industry analysis of the decline of the labour share (Social, Employment and Migration Working Papers 133, julio). OECD. [ Links ]
4. CAHUC, P. y ZYLBERBERG, A. (2004). Labor economics. Londres: MIT press. [ Links ]
5. CÁRDENAS, M. y GUTIÉRREZ, C. (1998). "Determinantes del desempleo en Colombia", Debates de Coyuntura Social, mayo, Fedesarrollo-Fundación Corona. [ Links ]
6. CLAVIJO, S. (1990). "Productividad laboral, multifactorial y la tasa de cambio real en Colombia", Ensayos sobre Política Económica, 17:73-97. [ Links ]
7. CLAVIJO, S. (2003). Crecimiento, productividad y la "nueva economía": Implicaciones para Colombia (Borradores de Economía 228). Banco de la República. [ Links ]
8. DAVIS, S. J. y HALTIWANGER, J. (1992). "Gross job creation, gross job destruction, and employment reallocation", Quarterly Journal of Economics, 107(3):819-863. [ Links ]
9. ECHAVARRÍA, J., ARBELÁEZ, M. A. y ROSALES, M. F. (2006). "La productividad y sus determinantes: el caso de la industria colombiana". Disponible en http://www.banrep.gov.co/docum/ftp/borra374.pdf. [ Links ]
10. ECHAVARRÍA, J., LÓPEZ, E., OCAMPO, S. y RODRÍGUEZ, N. (2011). Choques, instituciones laborales y desempleo en Colombia (Borradores de Economía 682). Banco de la República. [ Links ]
11. ESLAVA, M., HALTIWANGER, J., KUGLER, A. y KUGLER, M. (2005). "Employment and capital adjustments after factor market deregulation: Panel evidence from Colombian plants". Disponible en http://www.banrep.gov.co/documentos/conferencias/2006/ac_ehkk_060105.pdf. [ Links ]
12. GONZÁLEZ, A., OCAMPO, S., RODRÍGUEZ, D. y RODRÍGUEZ, N. (2011). Asimetrías del empleo y el producto, una aproximación de equilibrio general (Borradores de Economía 663). Banco de la República. [ Links ]
13. GRUPO DE ESTUDIOS DEL CRECIMIENTO ECONÓMICO COLOMBIANO (GRECO) (2002). El crecimiento económico colombiano en el siglo XX. Bogotá: Fondo de Cultura Económica. [ Links ]
14. GUTIÉRREZ, C. (2012). Trade and technology: Descomposing the rise of the skill premium in the Colombian manufacturing sector (Documentos de Trabajo 1, marzo). EGOB. [ Links ]
15. GUTIÉRREZ, C. y LESMES, J. (2012). Progreso tecnológico incorporado en el capital y sus efectos en el desempleo. Manuscrito no publicado. [ Links ]
16. HORNSTEIN, A., KRUSELL, P. y VIOLANTE, G. L. (2005). "The replacement problem in frictional economies: A near-equivalence result", Journal of European Economic Association, 3(6):1007-1057. [ Links ]
17. HORNSTEIN, A., KRUSELL, P. y VIOLANTE, G. L. (2007). "Technology-policy interaction in frictional labour market", The Review of Economic Studies, 74(4):1089-1124. [ Links ]
18. LESMES, J. (2012). Progreso tecnológico incorporado en el capital y desempleo en Colombia. Manuscrito no publicado. [ Links ]
19. LOAYZA, N., FAJNZYLBER, P. y CALDERÓN, C. (2002). Economic growth in Latin America and the Caribbean. Stylized facts, explanations and forecasts. Washington: The World Bank. [ Links ]
20. MONDRAGÓN-VÉLEZ, C., PEÑA, X. y WILLS, D. (2010). Labor market rigidities and informality in Colombia (Documento CEDE 7, febrero). Universidad de los Andes, Facultad de Economía. [ Links ]
21. MORTENSEN, D. y PISSARIDES, C. (1998). "Technological progress, job creation, and job destruction", Review of Economic Dynamics, 1(4):733-753. [ Links ]
22. NÚÑEZ, J. y BERNAL, R. (1997). "El desempleo en Colombia: tasa natural de desempleo cíclico y estructural y la duración del desempleo, (1976-1998)", Ensayos sobre Política Económica, 32:7-74. [ Links ]
23. PETRONGOLO, B. y PISSARIDES, C. (2001). "Looking into the black box: A survey of the matching function", Journal of Economic Literature, 39(2):390-431. [ Links ]
24. PISSARIDES, C. (2000). Equilibrium unemployment theory. Londres: MIT press. [ Links ]
25. PISSARIDES, C. y VALLANTI, G. (2007). "The impact of TFP growth on steady-state unemployment", International Economic Review, 48(2): 607-640. [ Links ]
26. PRAT, J. (2007). "The impact of disembodied technological progress on unemployment", Review of Economic Dynamics, 10(1):106-125. [ Links ]
27. RAMÍREZ, J. y NÚÑEZ, L. (2000). "Reformas, crecimiento, progreso técnico y empleo en Colombia. Parte II", Reformas Económicas, 59, CEPAL. [ Links ]
28. RHENALS, R. y BASTIDAS, A. (2007). "Cambio técnico y empleo: a propósito del menor dinamismo relativo de la ocupación industrial en Colombia, entre 1976 y 2005", Perfil de Coyuntura Económica, 10:91-127, diciembre. [ Links ]
29. RODRÍGUEZ, J., PERILLA, J. y REYES, J. (2004). Cálculo del PIB potencial en Colombia: 1970-2003 (Archivos de Economía, 261). DNP-DEE. [ Links ]
30. SALA-i-MARTIN, X. (2000). Apuntes de crecimiento económico. Barcelona: Antoni Bosch. [ Links ]
31. SÁNCHEZ, F., DUQUE, V. y RUÍZ, M. (2009). Costos laborales y no laborales y su impacto sobre el desempleo, la duración del desempleo y la informalidad en Colombia, 1980-2007 (Documento CEDE 11, abril). Universidad de los Andes, Facultad de Economía. [ Links ]
32. TAMAYO, J. (2008). La tasa natural de desempleo en Colombia y sus determinantes (Borradores de Economía 491). Banco de la República. [ Links ]
33. WENGEL, J. (2006). "Creación y destrucción del empleo en la industria colombiana", Revista de la Información Básica, 1(2), artículo 4. Disponible en https://www.dane.gov.co/revista_ib/html_r2/articulo4_r2.htm. [ Links ]
Anexos
Anexo 1. Sistema de ecuaciones expresado en función del producto marginal del factor trabajo (φ)
De acuerdo con la sección IV(A), para la calibración de las variables y parámetros no observables en los datos (ω, θ y m0), con el supuesto de λ = 1, se utiliza el siguiente sistema de ecuaciones:
De esta manera se tiene un sistema de ecuaciones exactamente identificado de tres ecuaciones (A1.1, A1.2 y A1.3) con tres incógnitas (ω, θ y m0). Siguiendo a Pissarides y Vallanti (2007), para calibrar los valores no observables especificados sin necesidad de calibrar el producto marginal del factor trabajo (φ) las ecuaciones del sistema deben reexpresarse en función de este parámetro. Para esto se asume que b y c son proporcionales a φ. A partir de los datos para Colombia durante el periodo 1996-2000 y lo encontrado por Pissarides y Vallanti (2007):
Entonces, reemplazando (A1.4) y (A1.5) en (A1.1):
Introduciendo (A1.5) y (A1.6) en (A1.2) se tiene que:
Después de algunas operaciones, (A1.7) puede expresarse como:
Como la ecuación (A1.3) no está en función de φ permanece inalterada. Entonces, después de expresar las ecuaciones en función de φ, el sistema de ecuaciones que se utiliza para calibrar los valores desconocidos es:
Anexo 2. Información de la tasa de crecimiento de la PTF
La tasa de crecimiento de la PTF se toma de Rodríguez et al. (2004), quienes la calculan para el periodo 1970-2002. Esta es producto de un ejercicio de contabilidad de crecimiento, donde se asume una función de producción Cobb-Douglas:
donde el nivel de producción de la economía (Yt) es el resultado de una combinación de capital (Kt) y trabajo (Lt) y la productividad multifactorial (At). α y β son positivos e indican la elasticidad del capital y el trabajo en la función de producción. Debido a que el stock de capital presente en la economía no siempre se emplea en su totalidad, se ajusta por la utilización de la capacidad instalada (UCI). Además, Rodríguez et al. (2004) introducen la variable de importación de bienes intermedios (BMI), que busca capturar los efectos del comercio internacional en la tasa de crecimiento de la economía. Entonces, la función estimada es:
El crecimiento de la productividad se encuentra según el residuo de Solow.
Pasando (A2.2) a logaritmos, diferenciando esta nueva ecuación y utilizando los parámetros estimados, se obtiene:
De acuerdo con Rodríguez et al. (2004), la fuente de la serie del PIB real son las estadísticas históricas del Grupo de Estudios del Crecimiento Económico Colombiano (GRECO), del Banco de la República, desde 1970 hasta 1994. Con los crecimientos de esta serie y con los datos que reporta el DANE desde 1994 del PIB real, se encuentra una serie consistente de PIB, en pesos de 1994. La estimación del stock de capital se hace de acuerdo con el método de inventario permanente. Para encontrar la inversión se unen los datos de formación bruta de capital fijo desde 1925 hasta 1990 con los datos de las nuevas cuentas nacionales desde 1990 hasta 2002. La fuente de la serie de la UCI es la Fundación para la Educación Superior y el Desarrollo (Fedesarrollo). Esta variable se encuentra desde 1981 hasta la fecha. Para encontrar los datos hacia atrás se usa una proxy construida a partir del comportamiento del PIB. Rodríguez et al. (2004) aprovechan la serie de empleo nacional estimada por Barrios, Henao, Posada, Valderrama y Vásquez (1993) para el periodo 1951-1992. A partir de 1991 se utilizan los datos del módulo de septiembre de la ENH hasta el año 2000. Para establecer las importaciones de bienes intermedios (BMI) utilizan la serie de importaciones de balanza de pagos, expresadas en dólares.
Anexo 3. Calibración del modelo de progreso tecnológico no incorporado, 1991-1995
Al igual que en la sección IV(A), también se realiza la calibración de los valores del salario de reserva (ω), la estrechez del mercado laboral (θ) y la constante de la función de encuentros (m0) para el periodo 1991-1995, suponiendo que el progreso tecnológico es totalmente desincorporado, λ = 1. Los resultados de este ejercicio, en particular el valor de m0, se usan para los ejercicios de simulación de la sección IV(B.4). El sistema de ecuaciones viene dado por:
La variable y parámetros observables se toman de las mismas fuentes que se describieron en la sección IV(A.2), pero en este caso para el periodo 1991-1995 (véase cuadro A3.1).
Del respectivo ejercicio de calibración se obtienen las siguientes soluciones para las variables y el parámetro desconocidos del modelo (véase cuadro A3.2).
Estos valores se interpretan de forma similar a la encontrada en la sección IV(A.3). Para ver si los parámetros calibrados son robustos ante variaciones razonables de los parámetros asumidos (β, η y c), se realiza el mismo ejercicio de robustez de la sección IV(A.3), y se obtiene que los parámetros ω, θ y m0 sí son robustos ante variaciones en los parámetros asumidos. Los resultados se muestran en cuadro A3.3.