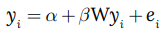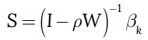Introducción
A finales de 2019 e inicios de 2020, se informó al mundo del surgimiento de un nuevo coronavirus, que estaba causando un tipo de neumonía que no respondía a los tratamientos habituales, y cuya capacidad de contagio advertía del surgimiento de una pandemia (Gross et al., 2020). Al cabo de los meses, el virus se expandió en todos los países y, desde entonces, ha concentrado el interés de académicos y científicos por entender sus patrones y sus particularidades, desde múltiples perspectivas (Franch-Pardo et al., 2020). Los modelos epidemiológicos para dividir la población en grupos, como los del tipo susceptibles- infectados-recuperado (SIR) y del tipo sensible, expuesto, infectado, removido (SEIR), empezaron a ser adaptados y aplicados a múltiples situaciones; además, fueron considerados para orientar las políticas públicas de choque ante el avance del virus en muchos países, como las medidas de cuarentena estricta y las prácticas de bioseguridad dentro del establecimientos público-privados (He et al., 2020).
Luego de casi cuatro años de iniciada la pandemia, el proceso de vacunación ha avanzado de manera importante en todo el mundo y ha permitido reducir los riesgos de hospitalización y de muerte. Pero las nuevas variantes, en especial las variantes denominadas “JN.1” y “BA.2.86”, han enfrentado al mundo a escenarios de contagio mucho mayores, lo que impone la necesidad de establecer políticas de salud pública que le hagan frente a las amenazas que pueden significar para ciertos segmentos poblacionales, y que puedan prevenir el colapso eventual de los sistemas de salud de los países, una preocupación constante desde el surgimiento de la pandemia.
La literatura se ha concentrado en discernir el efecto del surgimiento y el desarrollo de la pandemia sobre la desigualdad y el crecimiento económico entre países y dentro de estos, desde la perspectiva subregional (Furceri et al., 2022). En general, estos efectos se han dividido en aquellos de corto plazo y otros de largo plazo: dentro de los primeros, se ha señalado el cierre de empresas —particularmente en el caso de empresas pequeñas (Belitski et al., 2022)—, el crecimiento de la pobreza y desigualdad, entre otros (Murshed, 2022).
Dentro de los efectos de largo plazo, los académicos advierten importantes efectos en los costos de los insumos, y una aceleración en la adopción de empleos, que implican transformación tecnológica en empresas, sustituyendo empleos de menor cualificación técnica (Petropoulos, 2021), así como efectos importantes en la calidad de la educación. Estos efectos, ciertamente, tienen efecto en la distribución del ingreso y los patrones de desigualdad, especialmente, en países en vías de desarrollo. La direccionalidad y el orden de magnitud de los impactos de corto y de largo plazo dependen, entre otros aspectos, de la velocidad de transmisión del virus, su capacidad de contagio y su mortalidad (Bourdin y Levratto, 2023).
Uno de los aspectos que más ha llamado la atención de los académicos en todo el mundo ha sido la velocidad de contagio del virus (Tang et al., 2020). Esta velocidad ha dependido de muchos factores, como el nivel de movilidad e interacción, la predisposición biológica y médica, así también, de otros factores de naturaleza económica y social (Chen et al., 2020). Esta dinámica de velocidad de difusión se ha seguido entre los territorios, por lo que poder analizar su comportamiento espacial resulta crucial para apoyar la formulación de políticas orientadas a su mitigación.
En este sentido, las técnicas de análisis espacial han permitido complementar los ejercicios de estadística sobre los patrones de propagación del virus (Franch-Pardo et al., 2020). En efecto, la modelación de los patrones espaciales de contagios, muertes y recuperaciones puede ayudar a entender la forma en que el virus se expande en un territorio o entre territorios, y poder explicar, además, los factores que inciden en sus niveles de intensidad para diferentes contextos. Si las medidas adoptadas por la gran mayoría de los países tenían el objetivo de frenar la interacción entre personas, localidades y regiones, la forma como actúa el virus comporta un proceso de dependencia espacial y su dinámica en el espacio no debería ser aleatoria, dado que depende de una mayor o menor interacción entre agentes, localidades y regiones.
El presente trabajo tiene el objetivo de analizar y caracterizar el proceso de dependencia espacial de los contagios del Covid-191 para el departamento de Antioquia, Colombia, a partir de su escala municipal. En concreto, la pregunta que encausó la investigación fue la siguiente: ¿cuál es la capacidad de contagio espacial —spillo- ver espacial— municipal del Covid-19, durante el curso de la pandemia en el departamento de Antioquia y las características de su patrón subregional? Para el periodo 2020-2021, con periodicidad mensual, se recaba evidencia que permite discernir el patrón espacial de los contagios y, posteriormente, se propone una métrica de capacidad de difusión espacial del virus, la cual es útil para ranquear a los territorios respecto a su capacidad de contagiar a otros. Por medio de análisis de indicadores locales de asociación espacial (LISA, por sus siglas en inglés) se estudian los procesos de clusterización de contagios y su evolución en el periodo de estudio, contrastando los momentos de mayores y menores contagios, así como el proceso de vacunación realizado en el territorio.
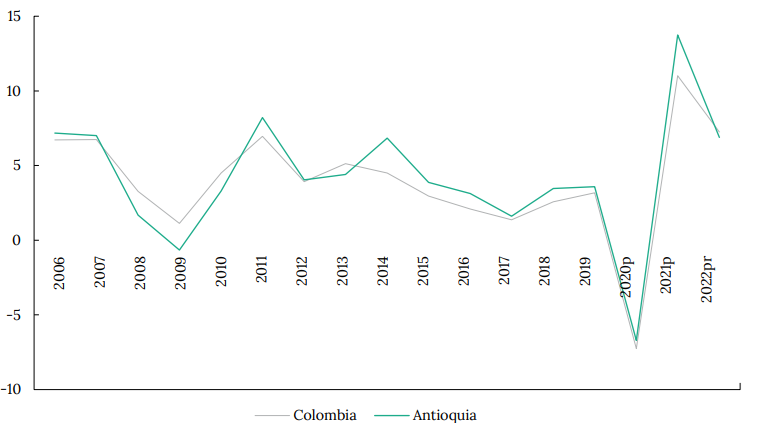
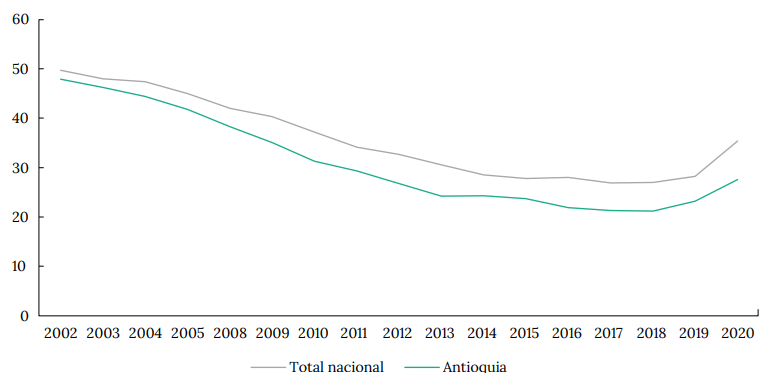
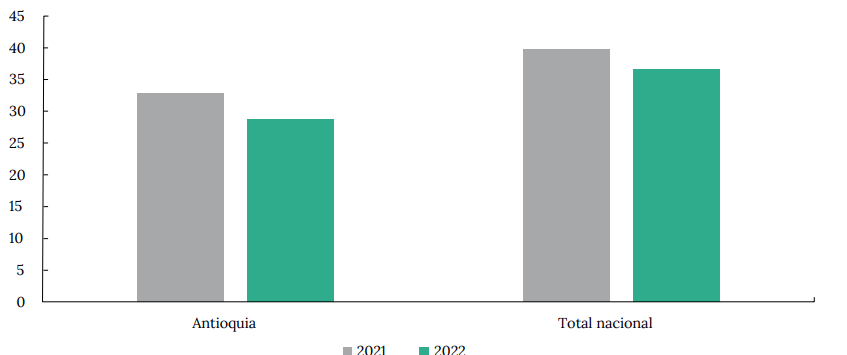
Disponer de la información referente a la capacidad de contagio permite abordar investigaciones más profundas sobre el efecto del Covid-19, en el crecimiento económico y la desigualdad, fenómenos de particular importancia en el contexto colombiano. Por ejemplo, en la figura A1 del Anexo, se presenta la caída de la actividad económica en Antioquia, comparado con el comportamiento nacional, la cual llegó a -6.71 % en el año más incidente de los contagios y donde fue especialmente significativa la capacidad espacial de contagio subregional. De manera paralela, los Anexos A1 y A2 permiten evidenciar el incremento de la pobreza extrema en el departamento, como un cambio estructural del comportamiento tendencial decreciente prepandemia.
En lo que concierne a los efectos de corto y largo plazo sobre la desigualdad y la pobreza, una parte de la literatura nacional se ha concentrado en el impacto sobre la calidad de la educación (Vegas, 2022), los efectos de la mortalidad (Cifuentes et al., 2021), e incluso los impactos de la participación laboral de las mujeres durante y después de la pandemia (Tribin et al., 2023). De esta manera, los resultados encontrados permiten soportar información complementaria importante a la agenda de investigación actual.
Un estudio sobre el departamento de Antioquia es importante por tres razones, entre otras: en primer lugar, es una de las economías regionales más fuertes de Colombia, con uno de los niveles de cobertura en salud y redes hospitalarias más eficientes (García, 2014), lo cual permite hacer comparativos relevantes del comportamiento del virus con respecto a otras regiones del país2. En segundo lugar, su estructura económica no es homogénea y se caracteriza por estructurales disparidades de ingreso (Galvis-Aponte et al., 2017; Vélez-Tamayo et al., 2022) entre el centro económico -aglomerado alrededor de su área metropolitana predominantemente urbana y las áreas periféricas de características rurales generalizadas, un aspecto importante para explicar las capacidades de contagio subregional del virus. En tercer lugar, su ubicación en el sistema geográfico del país es central, con una amplia accesibilidad a múltiples regiones, por lo que la evolución de la pandemia en todo el territorio nacional depende, de igual manera, de lo experimentado por estos grandes departamentos en su interior3.
El artículo está dividido en cuatro secciones, incluyendo la introducción. En la segunda, se propone la revisión de literatura sobre aplicaciones de análisis espaciotemporal aplicado al Covid- 19, así como el estado del arte técnico sobre la forma de capturar efectos de difusión especial —spillover espacial—. En la tercera sección, se examinan los datos y los procedimientos de econometría espacial aplicados. En la cuarta, se presenta la evidencia recabada y, por último, se dan a conocer las conclusiones y se hacen algunas recomendaciones.
I. Revisión de literatura y marco teórico
La presente sección se divide en dos apartados. En primer lugar, se describe la literatura sobre la forma en la que las técnicas de análisis espacial se han aplicado para analizar los contagios de Covid-19. En segundo lugar, se procede a ilustrar las metodologías de econometría frecuentemente utilizadas en estos trabajos, así como la forma en la que se calculan efectos spillover.
A. Revisión de literatura sobre análisis espacial aplicado al Covid-19
Desde su surgimiento, el número de investigaciones sobre el Covid-19 ha tenido un crecimiento significativo, en muchas áreas y disciplinas4. Esto también ha ocurrido con respecto a la aplicación del análisis espacio-temporal y geográfico sobre la pandemia (Franch-Pardo et al., 2020). Uno de los primeros trabajos que aplicaron sistemas de información geográfica (GIS, por sus siglas en inglés) fue el de Guan et al. (2020). En este trabajo, los autores caracterizan el perfil de 1099 pacientes confirmados y analizan estas características a nivel de provincia. La importancia del trabajo reside en dilucidar el mecanismo de difusión espacial del virus, a través de las características de los pacientes, y considera su epicentro a la ciudad china de Wuhan. Chen et al. (2020), por su parte, parametrizan el análisis espacial a partir de técnicas bayesianas y se concentran en el proceso migratorio como factor explicativo del contagio. Si bien la presente investigación no toma factores explicativos relacionados con la migración, sí adopta la estrategia de los autores anteriores para analizar comportamientos de epicentros de contagio.
A partir de estos trabajos pioneros, la literatura se ha concentrado en aplicar el análisis GIS y espaciotemporales a escalas regionales variables y en múltiples países. Esta literatura se dirige a estudiar la evolución del virus de acuerdo con factores de movilidad (Huang et al., 2020), por un lado, y explicar los agrupamientos de los eventos de contagio en relación con procesos de aglomeraciones urbanas (Desai, 2020), pero la mayoría de los trabajos analiza los efectos de las medidas de cuarentena estricta mediante este enfoque espacial5. En China, por ejemplo, Gross et al. (2020) estudiaron la difusión del virus con las migraciones anteriores a las medidas de cuarentena ejecutadas, a partir de lo cual encontraron que la propagación del virus sigue procesos fractales propios de la movilidad humana, como el llamado vuelo de Levy. En una línea similar, se destaca el trabajo de Tang et al. (2020). Sun et al. (2021), por su parte, analizan los patrones espaciales de contagios y cómo se diferencian dependiendo de áreas consideradas. Por su lado, Xue Wang et al., 2020) analizan la relación de los contagios con procesos de movilidad intra-urbana capturados por un índice de transporte.
Para Rossman et al. (2020), en el caso de Israel, se advierte que los patrones espaciales de contagio pueden incluso variar y depender del nivel de escala del análisis o del nivel de resolución, aspecto que obliga considerar distintas matrices de pesos espaciales y unidades de análisis. Para Estados Unidos, Desjardins et al. (2020) realizaron el análisis de agrupamientos de contagios a nivel de condado con alta frecuencia temporal para identificar clústeres y establecer el efecto de las medidas de cuarentena en la mitigación de los nuevos contagios.
En la misma línea se encuentran el trabajo de Gao et al. (2020). En tal sentido, Orea y Álvarez (2022), para España, encuentran que las medidas de cuarentena estricta practicadas tuvieron un efecto sobre la mitigación de contagios. Asimismo, Giuliani et al. (2020) para Italia a nivel de condado, advierten de la existencia de heterogeneidad en los procesos de contagio entre la parte norte y sur del país. Además, si bien encuentran que las medidas de cuarentena estricta efectivamente mitigan los niveles de contagio, el efecto varía dependiendo del territorio y sus peculiaridades.
Por esta razón, en efecto, las capacidades de contagio de las unidades regionales son diferentes y se sujetan a múltiples factores (Gross et al., 2020).
La dinámica de contagio del virus puede ser aproximada no solo por la existencia de autocorrelación espacial, lo que se denomina análisis exploratorio de datos espaciales (Anselin, 2013), sino también por lo que se denomina el efecto spillover espacial (spillover effect) que implica la aplicación de métodos de econometría espacial o análisis confirmatorio de datos espaciales (LeSage et al., 2009). En este sentido, se destacan los trabajos de Guliyev (2020), quienes utilizan panel de datos espaciales a nivel regiones en China, correlacionando muertes y contagios. En la misma línea, Krisztin et al. (2020) utilizan métodos bayesianos para capturar, en un estudio entre países, la estructura de los efectos spillover espaciales, y demuestran que las restricciones de los viajes disminuyeron los efectos spillovers del virus. Asimismo, en Wong y Li (2020) se encuentra que la densidad poblacional es un predictor eficaz de los eventos de Covid-19 a nivel de Estado en Estados Unidos.
En cuanto a los estudios relativos a Colombia, las corrientes y métodos de análisis han sido similares a la literatura internacional, sin embargo, la literatura es escasa. Se destacan los trabajos de García (2020) y Cuartas et al. (2020) quienes aplican el análisis espacio-temporal para identificar clústeres a nivel de municipio y a nivel de barrio. Desde la perspectiva de la relación entre los flujos de transporte y la transmisión del virus en Colombia, podemos destacar el trabajo de Calatayud et al. (2022). Aplicaciones de parametrización bayesiana para el análisis espacial del Covid en Colombia se encuentra en Polo et al. (2020). Por otra parte, Ruiz y Barrera (2020) determina el efecto del incumplimiento de las medidas de cuarentena a partir de datos aportados por la policía para la ciudad de Bogotá. No obstante, no hay en la literatura nacional investigaciones relacionadas con la cuantificación concreta del efecto spillover a nivel subregional.
El estado del arte anterior permitió estructurar la estrategia empírica del presente trabajo en tres aspectos relevantes: en primer lugar, los análisis tipo clúster permiten discernir, cuando se evalúan los primeros contagios, los epicentros de difusión y la forma en la que el efecto spillover espacial opera en el territorio -especialmente útil para esto fueron los trabajos de Chen et al. (2020) y Guan et al. (2020) junto con las advertencias de Orea y Álvarez (2022) y Giuliani et al. (2020) sobre la variabilidad de la velocidad de difusión de acuerdo a características del territorio y la consideración de las matrices de pesos espaciales.
En segundo lugar, las metodologías comportan la posibilidad de evaluar el impacto de políticas de mitigación del virus, como las medidas de cuarentena y los procesos de vacunación, posibilidad llevada a cabo en la presente investigación al poder computar los cambios estructurales de los efectos de difusión antes y después de la ejecución de las políticas en el contexto colombiano. En tercer lugar, la literatura anterior abre la posibilidad de una agenda de estudio sobre los determinantes propios del patrón espacial de contagio, que permita evaluar el efecto de factores económicos, sociales y territoriales sobre la variabilidad de la difusión del virus. Las metodologías propuestas permiten disponer de métricas sobre las que, posteriormente, pueden hacerse investigaciones transdisciplinarias potentes para sustentar la formulación de políticas de salud pública.
B. Análisis espacial: efectos de difusión
El estudio de los llamados efectos difusión, o efectos spillovers, ha constituido en los últimos años un importante y cultivado campo de estudio en la llamada ciencia regional. El interés por conocer y cuantificar la forma en que la conexión espacial de ciertas unidades regionales incide sobre la difusión de sus dinámicas económicas, sociales e institucionales, no solo viene de la mano de la necesidad de establecer políticas económicas de impacto regional, sino también de enriquecer el cuerpo de teoría económica y practicas empíricas en el marco de los aportes de la nueva geografía económica (Krugman, 1991).
El análisis de los efectos spillovers ha partido del uso cada vez más frecuente de técnicas de estadística y econometría espacial, dedicados al estudio de múltiples fenómenos económicos e institucionales: por ejemplo, fenómenos de aglomeraciones urbanas (Grant y Vanderkamp, 1980; Dijk et al., 1990), spillovers tecnológicos (ver, por ejemplo, Fracasso y Vittucci, 2015; Keller, 2002), spillovers del gasto publico (Dall’erba & Le Gallo, 2008), entre otros. La idea subyacente es que gran parte de las variables económicas y sociales presentan una asociación espacial marcada, esto es, el valor de cierta variable económica, el PIB de una unidad regional, tomando un ejemplo ilustrativo, depende del valor que toma esta variable en sus vecinos más próximos. El hecho de que exista esta asociación espacial, y que precisamente las técnicas de estadística espacial permitan su cuantificación, ayuda a que puedan establecerse posibles efectos contagio de fenómenos ocurridos en una región particular sobre otras.
En tal línea, se ha establecido la existencia de dos tipos de efectos spillovers6. Por un lado, los llamados spillovers globales, los cuales se caracterizan porque la difusión, para un choque ocurrido en una región, es completa alrededor de la muestra, es decir, todas las unidades regionales experimentan tal difusión. Por otro lado, a diferencia de los spillovers globales, los locales son aquellos para los cuales la difusión ocurre no en toda la muestra, sino en los municipios mayormente cercanos. Estos spillovers locales no implican una matriz inversa (Anselin, 2013). De acuerdo con LeSage et al. (2009), los spillovers globales terminan siendo más difíciles de justificar desde un punto de vista económico que los locales, ya que los globales implican un efecto feedback, es decir, el choque de una región se difunde en las restantes y vuelve a la región inicial. Otros estudios como Gibbons et al. (2015), Arbia y Baltagi (2008) y el estudio de Lacombe y LeSage (2018) toman parte en esta discusión.
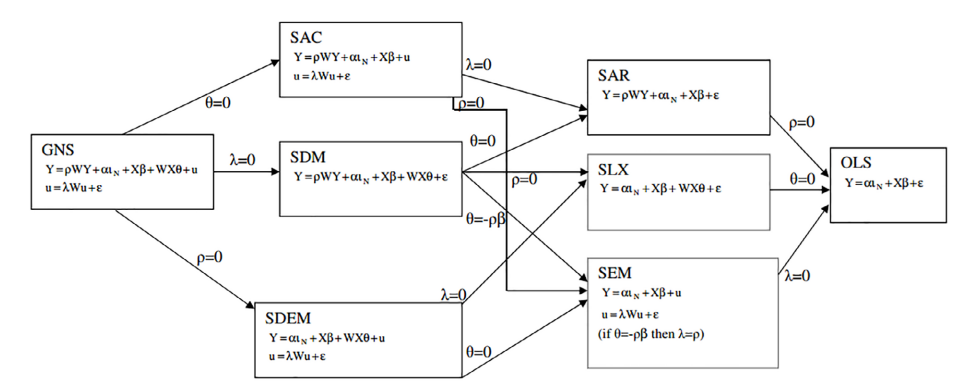
La literatura ha definido un conjunto de modelos de econometría espacial, particularmente útiles para determinar estos efectos spillovers. La figura 1 muestra estos modelos. La especificación tipo modelo espacial general anidado (GNS, por sus siglas en inglés) es la versión general que resulta de tomar un modelo con un error espacialmente autocorrelacionado, junto con rezagos espaciales tanto en las variables independientes como dependiente7.
De esta especificación general se desprende toda una gama de modelos, dependiendo de la significancia estadística de los coeficientes θ, λ y ρ. Las especificaciones más usuales en el desarrollo de análisis confirmatorio de datos espaciales tienen que ver con el modelo espacial autorregresivo (SAR), el cual solo presenta un rezago espacial de la variable dependiente, y el modelo de error espacial autorregresivo (SEM), donde se asume solo un error espacialmente autocorrelacionado. La elección del modelo depende, en buena medida, del tipo de spillover que el analista evalúe, tanto como de la mejor especificación que ajuste el comportamiento de los datos (Anselin et al., 2000).
El cuadro 1 muestra la forma del spillover que genera cada tipo de modelo econométrico. De acuerdo con el detallado inventario de Vega y Elhorst (2013), el modelo con rezago espacial en la variable explicativa (SLX) y la especificación de error espacial tipo (SDEM) permiten considerar spillovers locales. Entretanto, las especificaciones del tipo SDM permiten considerar efectos spillovers globales. De esta manera, el tipo de spillover que se va a analizar se encuentra, en cierta medida, supeditado al mejor ajuste posible de los datos, es decir, a criterios estadísticos.
Sobre especificaciones tipo SLX algunos autores han señalado la existencia de ciertas limitaciones para la interpretación de los spillovers locales. Por ejemplo, en el trabajo de Lychagin et al. (2016), se advierte que estos modelos reducen la dependencia de la estructura espacial a un único coeficiente. Por su parte, Halleck y Elhorst (2015) demuestra que la relación entre el efecto spillover y el efecto directo es el mismo para cada variable explicativa, lo cual es difícil de justificar en la práctica. Por otro lado, Pace y Zhu (2012) muestran que para estos modelos resulta posible que el coeficiente ρ afecte la estimación de los spillovers y, al mismo tiempo, la estimación de las perturbaciones espaciales (error espacial), de esta manera, se corre el riesgo de realizar estimaciones incorrectas.
En el trabajo de LeSage (2011), se establece una advertencia general metodológica sobre los potenciales problemas existentes en los modelos de econometría espacial que, en la mayoría de los casos, no se consideran cabalmente, debido al mayor énfasis que la literatura ha conferido a la sola estimación de los parámetros. El autor señala cuatro sesgos importantes: (1) incomprensión de los spillovers espaciales; (2) sensibilidad a la matriz de pesos espaciales; (3) regiones estacionarias para parámetros espaciales en modelos que envuelven múltiples matrices espaciales; y (4) la especificación correcta envuelve múltiples matrices espaciales.
Esa advertencia sugiere la necesidad de establecer especial atención en la matriz de pesos espaciales y en la posibilidad de someter las estimaciones iniciales a distintas matrices espaciales, en aras de testear la consistencia de los resultados. En línea con este trabajo, Lee (2009) establece la necesidad de incluir los aspectos dinámicos en las especificaciones espaciales, ya que la omisión temporal tiene implicaciones en la estimación misma de los parámetros. Por otro lado, señalan la posibilidad de existencia de cointegración espacial, debido a la integración de los mercados y a las aglomeraciones económicas. De esta manera sugieren que modelos con ecuaciones estructurales que tengan en cuenta también aspectos espaciales será un importante recurso para el futuro en ciencia regional.
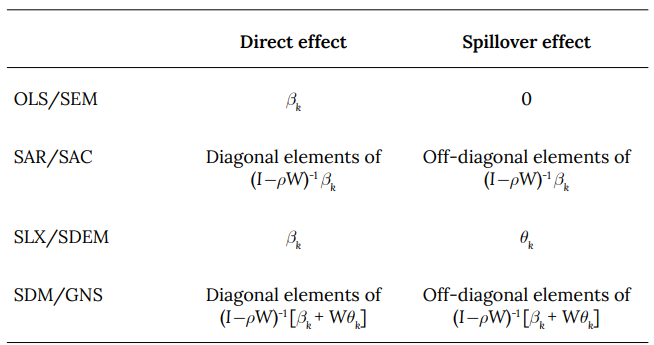
Fuente: tomado de Vega y Elhorst (2013).
Figura 2. Forma de los efectos spillover, según los modelos espaciales
Puede notarse, en el estado actual de la literatura, que los aspectos de orden metodológico-estadístico constituyen un campo de gran desarrollo, donde empiezan a vincularse nuevas perspectivas y técnicas. Por ejemplo, en Elhorst (2010) señala que una de las principales implicaciones del libro LeSage y Kelley (2009), consiste en plantear la posibilidad de nuevas técnicas, como las bayesianas, para definir qué tipo de matriz de pesos espaciales ayuda a describir mejor los datos. Así mismo, Vega y Elhorst (2013) argumentan la necesidad de endogenizar la matriz de pesos espaciales con propósitos similares. De esta manera, el debate en torno a los aspectos metodológicos no tiene signos de conclusión.
II. Metodología
La metodología implica dos etapas. Por un lado, la captura de datos para el análisis y, por otro, la escogencia de modelos econométricos y el estudio de los efectos spillover, como se indica a continuación.
A. Datos
A fin de llevar a cabo el análisis econométrico, se colectó información de contagios, sin discriminar por criterios como fallecidos o género, entre otros, a nivel municipal y con periodicidad mensual. No se tomaron los casos nuevos, ni los casos activos, sino los agregados. Ello, con el fin de capturar todo el resultado de contagios para el municipio al final del mes. Los datos se extrajeron del Ministerio de Salud de Colombia para el periodo 2020-M3—2021-M12. Los datos se concentran para el departamento de Antioquia, con 125 municipios distribuidos en diez subregiones.
B. Modelos econométricos y efectos spillover
Teniendo en cuenta los datos agregados de contagios a nivel mensual, se procedió, en primer término, a contrastar la hipótesis de dependencia espacial de esta variable. Para tal efecto, se utilizó una matriz de vecinos del tipo queen de primer orden8. Sobre esta matriz, se aplicó el estadístico de Moran global, bajo la especificación dada por la ecuación 1, donde Wij hace referencia a la matriz de vecinos y Xi hace referencia al dato de contagio para el municipio “i”; mientras que Xj indica el dato de contagio del municipio “j”. Los valores positivos de este indicador denotan una autocorrelación espacial positiva.
El índice de Moran global se emplea para evaluar la autocorrelación espacial en un conjunto de datos en su totalidad, a fin de determinar la presencia de un patrón global de similitud espacial. Por otro lado, el índice de Moran local (LISA por sus siglas en inglés) se utiliza para detectar la autocorrelación espacial a nivel local, esto es, para identificar la existencia de agrupaciones espaciales de valores similares en áreas específicas del conjunto de datos. Ello permite determinar la existencia de clústeres de asociación espacial y discernir el patrón de su comportamiento en el espacio. En lo sucesivo, la mayoría de los mapas elaborados presentan el Moran local, siguiendo la literatura de análisis espacial del Covid-19.
Una vez confirmada la hipótesis de dependencia espacial, se procedió a estimar el modelo referido en la ecuación 2, donde yi denota el número de contagios totales del municipio “i”, W la matriz de pesos espaciales y ei el componente de error estocástico sobre el que se espera pase los diagnósticos de heteroscedasticidad y autocorrelación correspondientes.
Cuando la especificación vincula un componente de error espacial, o error espacialmente autocorrelacionado, se considera que hay un componente espacial que no es explicado solamente por el comportamiento de los vecinos, estos modelos se conocen como modelos SAC (figura 1) o un Sarma. Con base en la ecuación 2 y la forma de cálculo de los efectos spillover referidos en el cuadro 1 se cuantificaron los efectos spillover promedio para cada municipio, de acuerdo con la ecuación 3, teniendo en cuenta los elementos fuera de la diagonal principal, como se indica en el cuadro 2 para el cálculo respectivo de dichos efectos, de acuerdo con Vega y Elhorst (2013).
III. Hallazgos
En esta sección se presenta la evidencia recabada a partir de la aplicación del análisis exploratorio y confirmatorio de datos espaciales, a los eventos de contagio del Covid-19 a nivel municipal. En primera instancia, se presenta un análisis de estadísticas descriptivas, en segundo lugar, el análisis exploratorio de datos espaciales y, finalmente, el análisis confirmatorio. Tal proceso de estadística espacial se basa en los derroteros contemplados en la literatura (Anselin et al., 2000; Arbia y Baltagi, 2008; Lacombe y LeSage, 2018).
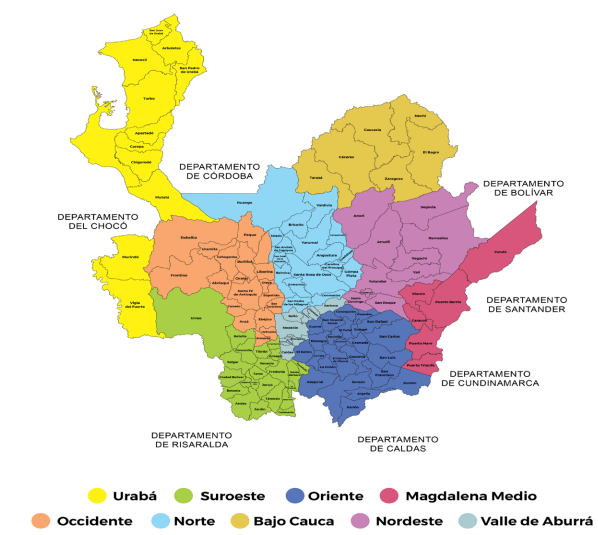
Resulta necesario caracterizar en términos geográficos generales al departamento de Antioquia –Colombia–, en el cual se circunscribe el análisis. El departamento se encuentra en el noroeste de Colombia y limita al norte con el mar Caribe. Su territorio se extiende desde las llanuras del bajo Cauca hasta las montañas de las cordilleras Central y Occidental de los Andes. Está compuesto por nueve subregiones (figura 3), donde la subregión del Valle de Aburrá, que contiene a la capital Medellín junto con otros nueve municipios, agrupa la mayor actividad económica del departamento, así como los mayores niveles de desarrollo.
Cuadro 1. Distribución espacial de la población y del índice de ruralidad 2019
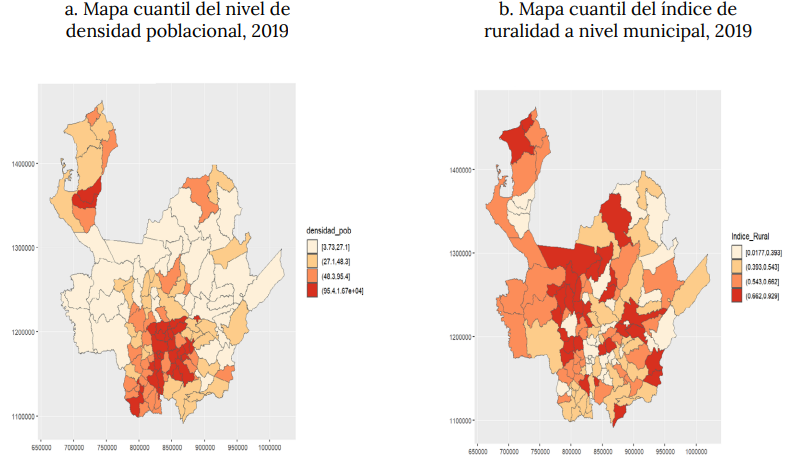
NotaLos ejes de los mapas corresponden a la proyección cartográfica nacional, equivalente al sistema WGS 48, para norte en el eje vertical y este para el eje horizontal.
Fuente: cálculos propios con base en el Dane y el Cider Universidad de los Andes.
En el cuadro 1, por su parte, se ilustra la distribución espacial tanto de un indicador de densidad poblacional, como del indicador de ruralidad para 20199. Como puede notarse, los municipios más densos corresponden a las subregiones del Valle de Aburrá y municipios del oriente cercano. Además, el mapa ilustra un patrón de conurbación importante, a partir del centro económico del departamento en Medellín, su capital. Por su parte, en los municipios más alejados de la capital, se configura una mayor presencia de características rurales, como puede notarse en el mapa B del cuadro 1.
Los hechos mencionados son relevantes para contextualizar y analizar el patrón espacial de los contagios de Covid-19 en el departamento. Los municipios más densos poblacionalmente exhiben una mayor probabilidad de contagios y dicha probabilidad se refuerza cuando las actividades económicas predominantes no son estrictamente rurales e implican mayores necesidades de interacción social, como los sectores de comercio y servicios, particularmente incidentes en las áreas de menor ruralidad.
A. Estadísticas descriptivas
El virus causante del Covid-19 hizo su aparición en Colombia en marzo de 2021. Desde entonces, se ha propagado a lo largo del territorio nacional, dejando a ningún municipio sin eventos de contagio. En el caso de Antioquia, el virus llegó también en el mismo mes de 2020 en su capital Medellín, desde donde se expandió a municipios cercanos, integrantes del área metropolitana, cuyo epicentro es justamente la capital del departamento y, luego, a otros municipios. Desde entonces, los eventos de contagio han tenido crecimientos y reducciones conformes con la adopción de medidas de cuarentena estricta y al avance del proceso de vacunación.
Como se nota en la figura 4, el comportamiento de contagio del virus a nivel departamental ha sido, en general, similar al ocurrido en Medellín desde inicios de la pandemia. Una ligera diferencia, conviene advertir, ocurrió en el pico de contagios del periodo de mayo-2021 a junio-2021, donde a nivel departamental, el mayor pico del año fue en el mes de junio con 104118 casos, en tanto que para Medellín fue en el mes de Abril, con 54 441 casos registrados. Este comportamiento conduce a la pregunta por el nivel de participación de la capital en los casos totales del departamento, como uno de los epicentros de contagio del virus, ya que la mayoría de los municipios del departamento mantiene relaciones socioeconómicas estrechas con este centro económico (Galvis-Aponte et al., 2017).
Con base en la figura 5, por ejemplo, puede notarse que en promedio la participación de la capital del departamento en el número total de contagios ha sido superior al 50 %. Solo en mayo del 2020 y junio del 2021, la participación en los casos totales fue menor al 50 %. Por su parte, en marzo de 2020 y en diciembre de 2021, la participación fue mayor, con 65 % y 68 % de los casos del departamento, respectivamente. Las figuras 4-5 ilustran un aspecto interesante: los momentos de mayor participación de la capital en el total de los casos no coincide, necesariamente, con el momento de los picos de contagios del departamento. De hecho, la mayor participación de Medellín se encuentra en el inicio de la pandemia y en diciembre de 2021, donde los niveles de contagio han disminuido significativamente gracias al avance del proceso de vacunación.
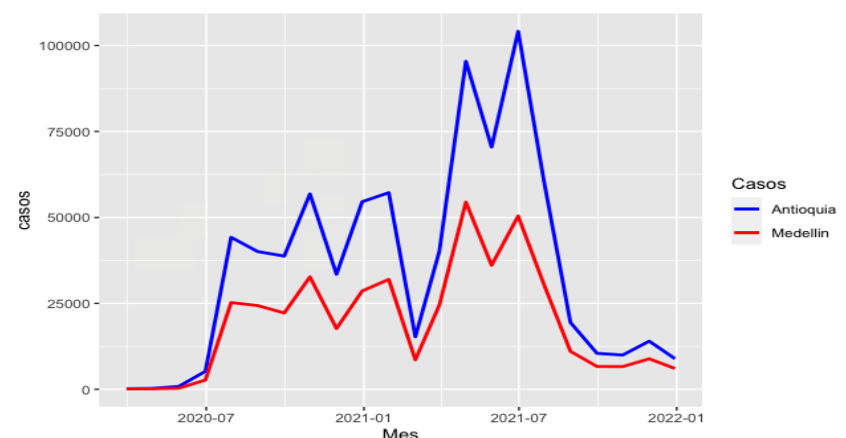
Fuente: elaboración propia a partir de datos del Ministerio Nacional de Salud.
Figura 4. Comparación de casos Antioquia y Medellín
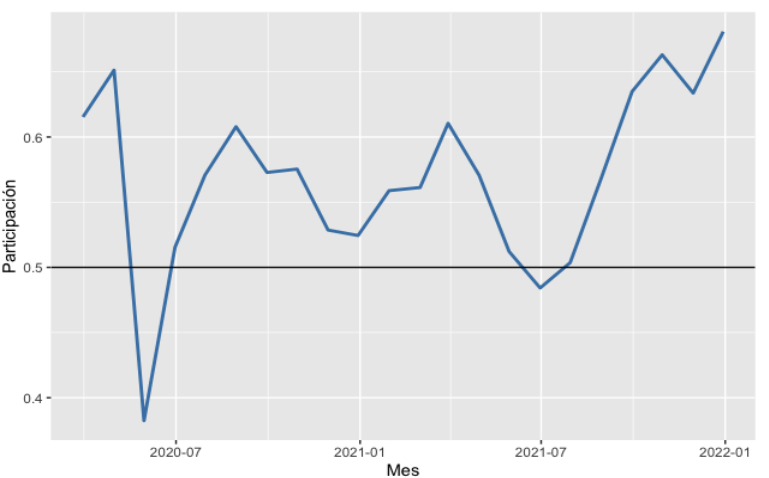
Fuente: elaboración propia a partir de datos del Ministerio Nacional de Salud.
Figura 5. Participación de Medellín en los casos totales
El que la capital muestre este comportamiento en su participación dentro de los casos totales departamentales es indicativo de su papel como municipio con mayor capacidad de contagio regional y, por tanto, con la posibilidad de que tenga mayor efecto difusión o spillover, debido a sus múltiples interacciones con municipios de la mayoría de las subregiones del país. Es indicativo, además, de la forma en que el virus se expande a través de las capitales de los departamentos más importantes de un país. En suma, lo que ocurre con las capitales ayuda a determinar el comportamiento de los departamentos o unidades regionales mayores, con respectivos rezagos temporales, de acuerdo con el avance del virus y las particularidades del territorio.
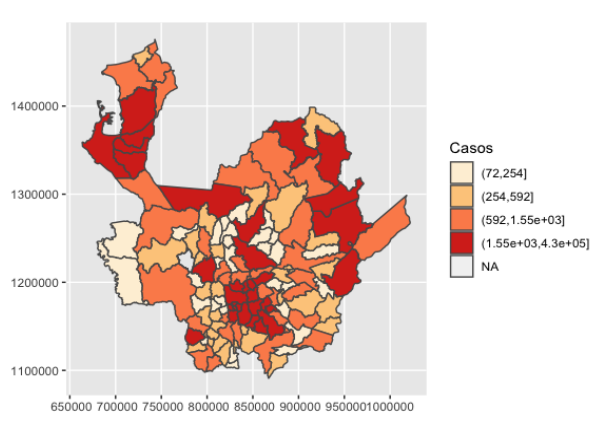
En el cuadro 2, se presenta el comparativo del mapa de contagios en el inicio de la pandemia y el correspondiente al mes de diciembre de 2021, de manera cuantílica. Como se indicó, el virus se presentó al inicio de la pandemia en Medellín y se expandió a partir de la capital hacia los municipios cercanos, Valle de Aburrá y subregiones del Oriente, Suroeste y Norte, principalmente. Sin embargo, la gran mayoría de las subregiones del departamento tiene municipios que, como Medellín, comportan altas capacidades de contagio intermunicipal, ya sea por su tamaño poblacional o por su mayor capacidad de interacción socioeconómica.
Los mapas anteriores permiten vislumbrar, de manera descriptiva, la existencia de un efecto contagio entre municipios, así como la presencia de municipios que, por sus características particulares, son grandes factores de contagio regional. El concepto de autocorrelación espacial entra aquí a desempeñar un papel importante: si hay dependencia espacial, autocorrelación espacial positiva, en los contagios (Anselin et al., 2000), indica que los niveles de contagio de un municipio dependen del nivel de contagios promedio de sus vecinos y que, por cuenta de esto, existe un efecto difusión intermunicipal que puede ser local o global, como se indicó en la sección metodológica. En el Anexo A4, se encuentra el mapa cuantílico que se genera al tomar los casos totales de contagio por municipio en el periodo 2020- 2021; como puede notarse, es similar al referido en el cuadro 1b.
Cuadro 2. Distribución espacial de los contagios, marzo de 2020 frente a diciembre de 2021
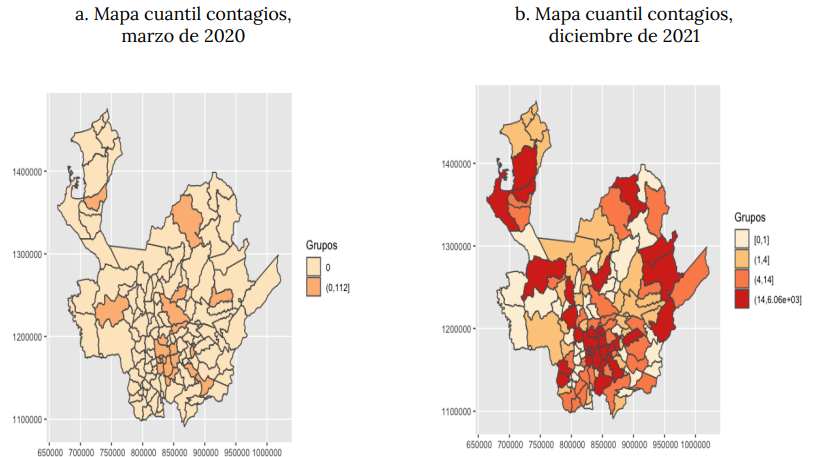
NotaLos ejes de los mapas corresponden a la proyección cartográfica nacional, equivalente al sistema WGS 48, para norte en el eje vertical y este para el eje horizontal.
Fuente: elaboración propia a partir de datos del Ministerio Nacional de Salud.
En el cuadro 3, se ilustran las estadísticas descriptivas a nivel departamental para el periodo de evolución del virus. En general, como se complementa gráficamente en el la figura A2 del Anexo, en los momentos de picos de contagios, aumentan la media y el grado de dispersión, lo cual ilustra las características del patrón de contagio al extenderse en el territorio: hay un municipio donde inicialmente ocurren los contagios, luego los municipios vecinos experimentan casos y, en dicho proceso, se forman, a su vez, otros municipios (en general las capitales de las subregiones) que presentan factores de contagios también altos, dispersando el virus; el proceso, desde luego, no es uniforme ya que los municipios presentan factores de difusión espacial distintos y, de igual manera, sus niveles de interacción son también diferentes por factores como el nivel de infraestructura vial, niveles poblacionales, ejecución y cumplimiento en las medidas de bioseguridad, entre otros.
B. Análisis exploratorio de datos espaciales
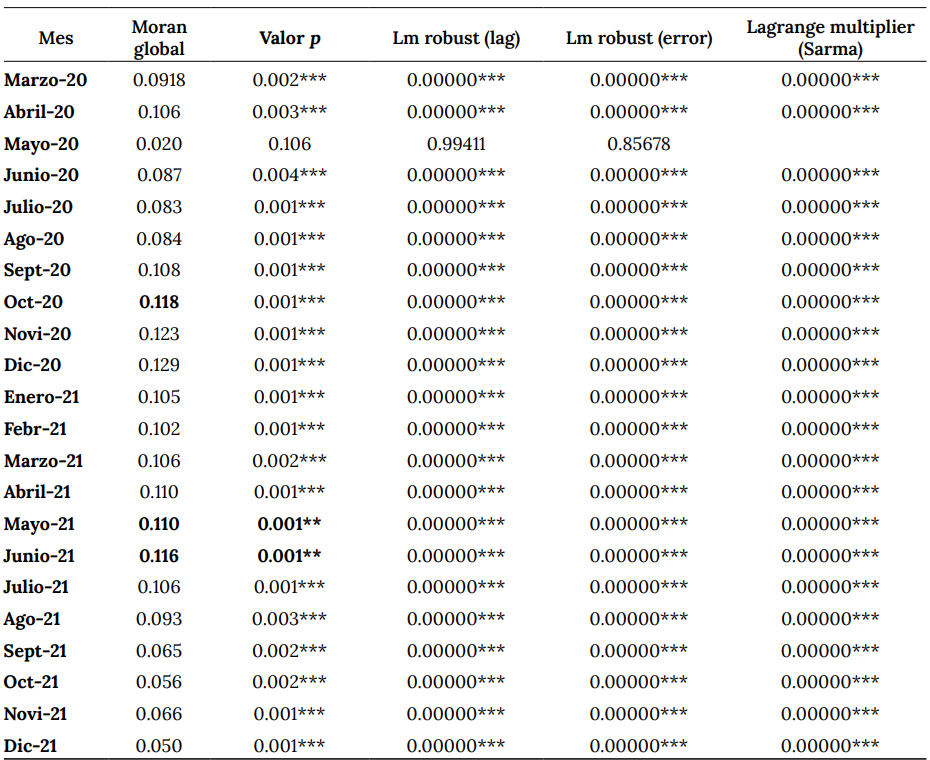
Como se indicó, el propósito de la presente investigación es caracterizar el patrón espacial de contagios a nivel municipal en el departamento de Antioquia. Por tanto, el primer paso consiste en la determinación de la existencia o no de dicho patrón espacial, porque el proceso de contagio puede ser aleatorio en su ubicación espacial. Este paso consiste, entonces, en testear la hipótesis de dependencia espacial y confirmar si el nivel de contagios de un municipio depende del nivel de contagios promedio que tengan sus vecinos más próximos, —autocorrelación espacial positiva (Anselin, 2013). Este proceso se hace a partir del cómputo de los estadísticos Moran global y Moran local, cuyas hipótesis de prueba fueron referidas en la sección metodológica. En el cuadro 3, se presentan los resultados de este test para cada mes considerado. De igual manera, se establece el test LM, para indicar la característica de la dependencia espacial, que indica si tal dependencia debe ser capturada con modelos de rezago espacial (Durbin), o bien con modelos de error espacial, ya que esto incide en el tipo de factor de difusión espacial o efecto spillover (Anselin, 2010).
Cuadro 3. Estadísticas descriptivas
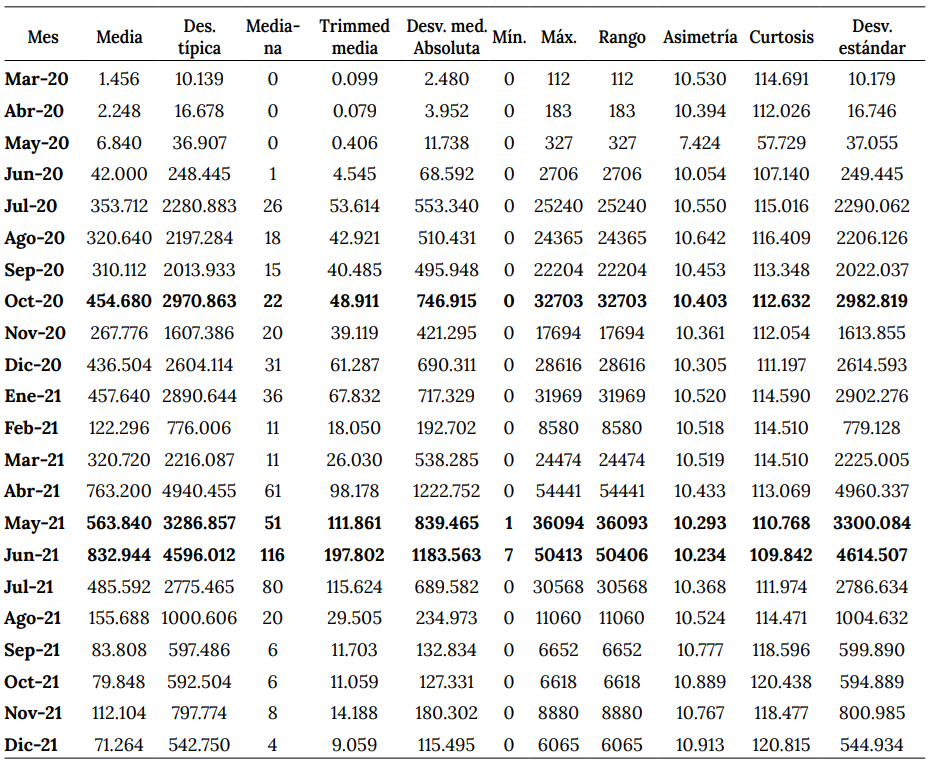
Fuente: elaboración propia a partir de datos del Ministerio Nacional de Salud.
El mismo cuadro 3 ilustra un proceso de dependencia espacial en todos los meses, salvo en mayo de 2020, caracterizado por autocorrelación espacial positiva. Por tanto, a nivel municipal puede concluirse que el Covid-19 experimentó un proceso de difusión espacial y que, más concretamente, el nivel de contagios que presenta un municipio en su interior no solo depende de factores propios, sino también del nivel de contagios de sus vecinos; si disminuye el nivel de contagio de sus vecinos, la probabilidad de que un municipio tenga altos contagios se reduce.
Asimismo, el cuadro 4 refleja un hecho interesante: en los momentos donde los niveles de contagios se incrementaron, como en octubre-2020 y mayo y junio de 2021, la intensidad de la dependencia espacial medido por el estadístico de Moran, fue también mayor, resultado acorde al anterior hallazgo de incrementos en el grado de dispersión del número de contagios. Por tanto, en los momentos de picos, el número de contagios se dispersa en el territorio por una mayor dependencia espacial a nivel subregional. Sin embargo, surge una pregunta: ¿qué motiva una mayor dependencia espacial en el virus? Una respuesta, no explorada a fondo aquí, tiene que ver con los mayores niveles de interacción socioeconómica entre municipios y al relajamiento de medidas de bioseguridad.
Al inicio de la pandemia, los municipios de las zonas rurales ejecutaron medidas de cuarentena estricta, así como la ejecución de restricciones de acceso de pobladores de otras regiones. Esto pudo limitar la capacidad de contagio intermunicipal. Sin embargo, su relajamiento pudo incrementar el efecto spillover de los municipios con mayor capacidad de difusión, como las capitales de las subregiones del departamento de Antioquia.
Cuadro 4. Estadísticos de dependencia espacial
***estadísticamente significativo al 99 % para hipótesis nula de aleatoriedad espacial.
**estadísticamente significativo al 95 % para hipótesis nula de aleatoriedad espacial.
*estadísticamente significativo al 90 % para hipótesis nula de aleatoriedad espacial.
Fuente: elaboración propia a partir de datos del Ministerio Nacional de Salud.
El cuadro 4 muestra, entonces, que existe dependencia espacial de los contagios en Antioquia y que esta debe ser estudiada, capturada, mediante la especificación de modelos Sarma, es decir, modelos que capturan el componente de rezago espacial; también el componente de error espacial (Lacombe y LeSage, 2018). El hecho de que el patrón espacial no sea capturado únicamente por el rezago espacial y que exista, por tanto, un componente residual de naturaleza espacial, es consecuencia del hecho de que solo se consideran aquí las dinámicas de contagios, pero no otros determinantes importantes que puedan tener un componente de dependencia espacial correlativo con la dinámica de contagios del virus (Gross et al., 2020). Por ejemplo, un determinante importante y que presenta dependencia espacial, es el conmuting laboral o el número de viajes entre municipios por motivos laborales, de negocios o de turismo, entre otros. Se espera que esta variable tenga una correlación muy estrecha con la dinámica de contagios y estaría, por tanto, en el componente espacial del residual de los modelos Sarma.
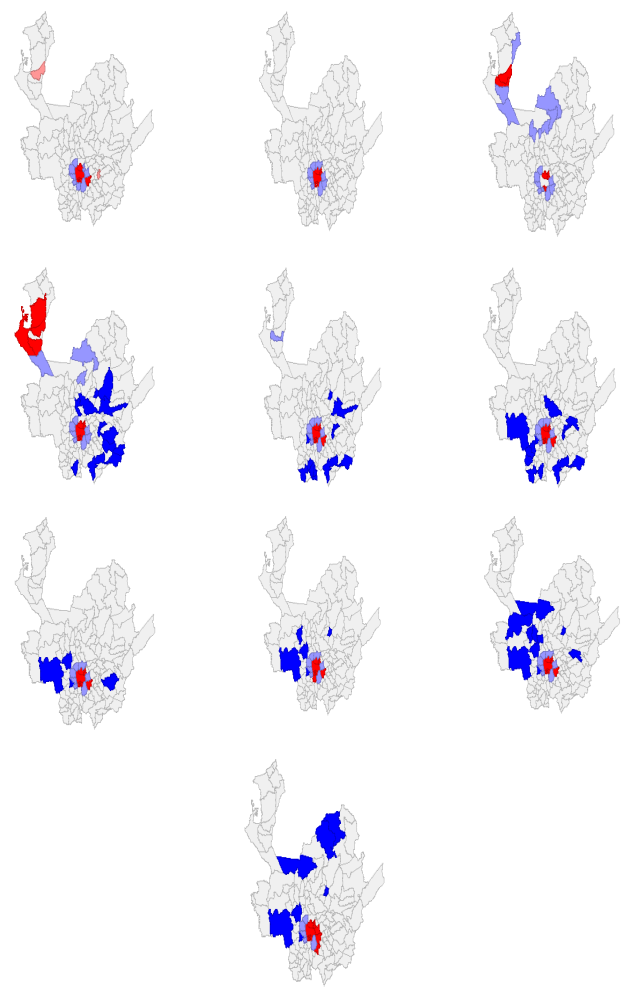
Un aspecto importante del proceso de análisis exploratorio de datos espaciales consiste en la estimación del Moran local. Este permite determinar la existencia de clústeres espaciales, que en el presente caso son agrupaciones de municipios de acuerdo con sus patrones y comportamientos de contagio. En el cuadro 4 se presenta una distribución de mapas del Moran local (mapas Lisa univariados) del número de contagios a nivel municipal. Es importante indicar el contexto de lectura: los municipios en rojo hacen parte del clúster HH (alto-alto), el cual corresponde a municipios que tienen un alto nivel de contagio y que, además, están en un vecindario de alto nivel de contagio promedio.
Por su parte, los municipios en azul oscuro son aquellos que integran el clúster LL (bajo-bajo) por tener bajos niveles de contagios y estar en un vecindario de bajo nivel de contagio promedio; en rosa se encuentran los municipios del clúster HL (alto-bajo) el cual agrupa a municipios que tienen alto nivel de contagios y que están en un vecindario de bajo nivel de contagios promedio; finalmente, el clúster LH (bajo-alto) en azul claro tiene municipios con un bajo nivel de contagio a pesar de estar un vecindario de alto nivel de contagios promedio.
La configuración de estos clústeres es importante, entre otras cosas, para focalizar los municipios donde mayores interacciones se generan y más capacidad de contagio existe. Además, permite evaluar cuáles municipios se salen del patrón general y, al mismo tiempo, explorar las medidas que han llevado a cabo. En el cuadro 5 se evidencia que la distribución de los clústeres es característico del nivel de importancia de Medellín y del Valle de Aburrá (área metropolitana) sobre la dinámica de contagios. En efecto, en el mapa Lisa de marzo de 2020, iniciada la pandemia en el departamento, se presenta un clúster alto- alto (en rojo) integrado por Medellín y municipios cercanos como Bello, Sabaneta, La Estrella y Envigado; y en la subregión del Oriente, el municipio de Rionegro.
Además, se destaca el municipio de Apartadó, en la subregión del Urabá, como un único clúster del tipo alto-bajo, es decir, un municipio con altos niveles de contagio, pero está en un vecindario de bajos niveles de contagio promedio. Este patrón centro se conserva en meses como mayo y junio del 2020, pero al final del año 2020 el clúster más persistente de alto nivel de contagio es el correspondiente a municipios del Valle de Aburrá, encabezado por Medellín.
La distribución espacial de los contagios con que finalizó 2020 es el mismo que tuvo lugar durante todo el año 2021 (Anexo A3). La existencia de otros clústeres del tipo alto-alto distintos a Medellín ya no tienen lugar en este año, lo cual puede ser consecuencia del avance del proceso de vacunación en el departamento y otras medidas practicadas. Sin embargo, las estimaciones del Moran local muestran que la capital del departamento, junto con los municipios más activos del Valle de Aburrá constituyen el centro de mayor posibilidad de expansión del virus a nivel subregional, por lo que rebrotes en estos municipios tienen el potencial de repercutir en todo el departamento. Por tanto, se espera que los mayores niveles de difusión espacial se encuentren en estas áreas departamentales10.
Dado que Medellín, por sí mismo, representa en promedio más del 50 % de los casos del departamento en 2020-2021, se computó el Moran local, eliminando a Medellín de la muestra, con el fin de poder visualizar el comportamiento del patrón espacial periférico sin la incidencia de los resultados de la capital. En los cuadros 6-7 se presentan los mapas del Moran local, excluyendo a Medellín de la muestra para 2020-2021. Los resultados permiten evidenciar lo que ocurre con las otras subregiones: al inicio de la pandemia, ciudades importantes de la mayoría de las subregiones constituían clústeres alto-bajo, para marzo de 2020. Hasta mediados de 2020, empezó a destacar la subregión del Urabá como un clúster del tipo alto-alto (rojo), con mayores capacidades de difusión del virus y, a finales de 2020, tomó de nuevo fuerza el clúster de municipios cercanos a Medellín, muchos de ellos del Valle de Aburrá, como La Estrella, Sabaneta y Caldas.
C. Análisis confirmatorio de datos espaciales
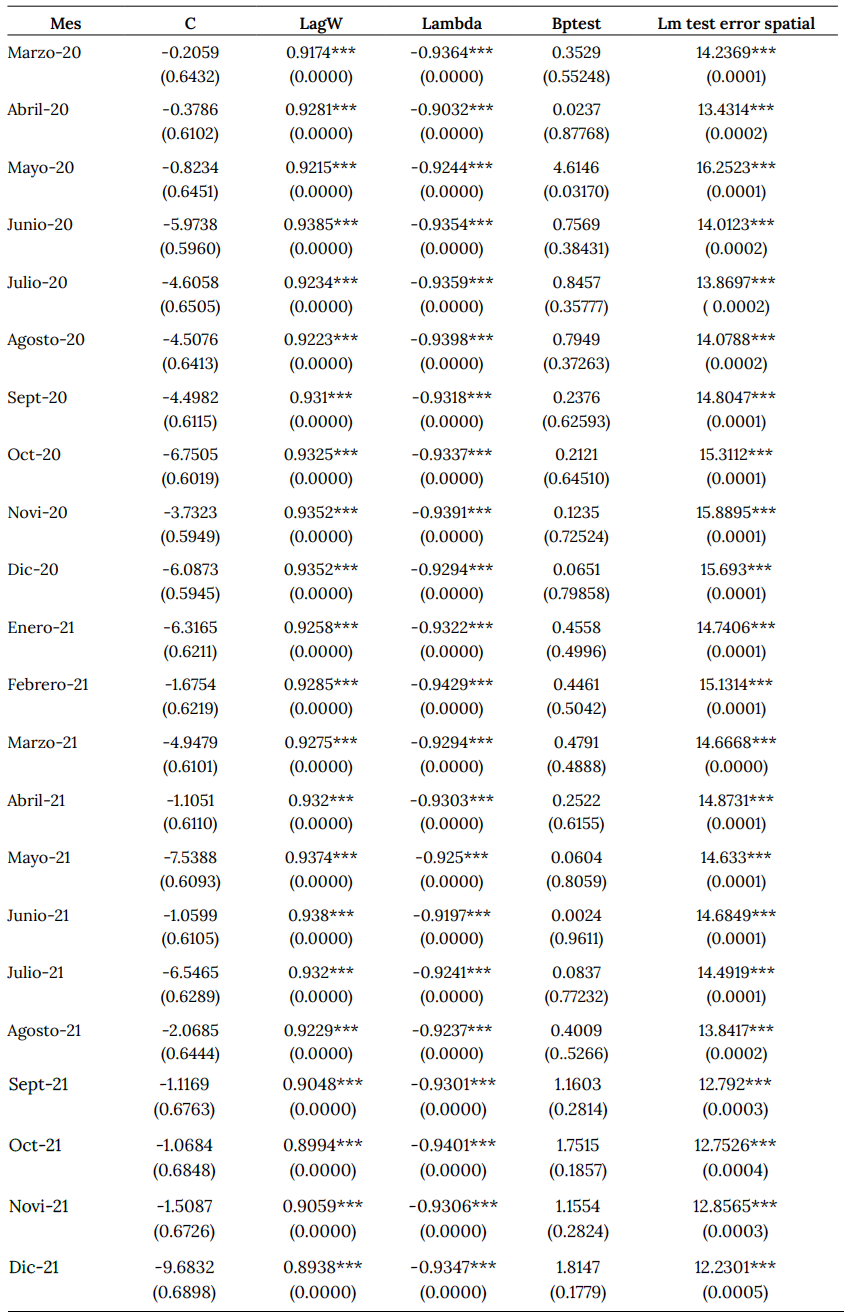
En la presente sección se ilustran los resultados derivados de la estimación de los modelos Sarma, sugeridos por los estadísticos de dependencia espacial. Dado que en todos los meses se confirma la hipótesis de dependencia espacial en el número de contagios, tratar de capturar la naturaleza del patrón espacial subyacente permite computar los efectos de difusión espacial y, con ello, discernir la capacidad de contagio regional del virus.
En el cuadro 8 se presentan los resultados de los ejercicios econométricos. En todos los modelos, estimados para cada mes, se encuentra significancia estadística en los componentes espaciales vinculados. En efecto, el coeficiente ρ del rezago espacial fue estadísticamente significativo y, además, de magnitud relativamente estable durante el periodo analizado. Asimismo, el coeficiente estimado λ del componente de autocorrelación espacial en el error, también fue estadísticamente significativo para todos los meses, con valores también estables a lo largo del periodo. Algunos coeficientes estimados cambian en los momentos de incremento de los casos de contagio, pero en general el patrón espacial capturado es estable en dicho periodo.
Un aspecto importante de las estimaciones tiene que ver con el signo de los parámetros espaciales: el coeficiente de rezago espacial es positivo, lo que indica auto correlación espacial positiva pero el coeficiente espacial del error es negativo. De acuerdo con Anselin (2010), LeSage et al. (2009) y Halleck y Elhorst (2015), cuando los modelos presentan un rezago espacial el efecto spillover obtenido es de naturaleza global, en tanto que los modelos de error espacial permiten discernir la existencia de un efecto spillover local (un ejemplo es el modelo SDEM). Por tanto, en los modelos Sarma, estos efectos se encuentran combinados. El valor similar, aunque con signo contrario, en los coeficientes estimados de los modelos del cuadro 7 no debe conducir a concluir que el efecto spillover es pequeño.
Cuadro 5. Moran local para 2020 (mapa de clústeres)
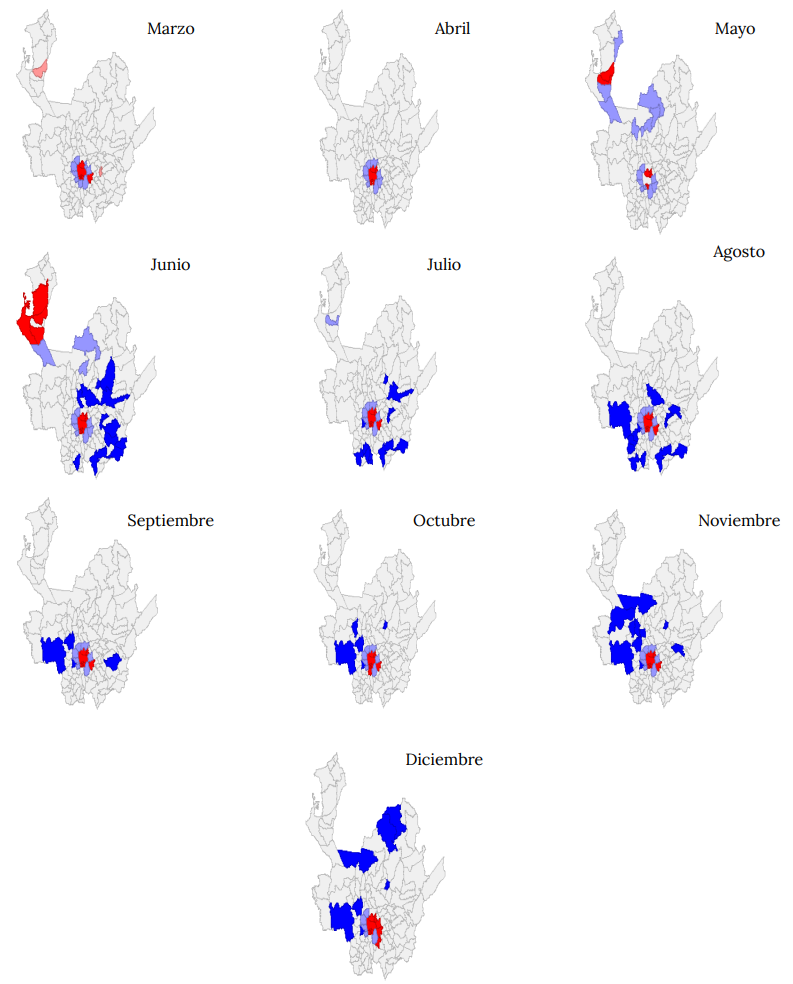
*El clúster HH (alto-alto) municipios en rojo. El clúster LL (bajo-bajo) municipios en azul. El clúster HL (alto-bajo) municipios en rosa. Clúster LH (bajo-alto) municipios en azul claro. Municipios en blanco, estadísticamente no significativos.
Fuente: elaboración propia a partir de datos del Ministerio Nacional de Salud.
Cuadro 6. Moran local para 2020, excluyendo a Medellín (mapa de clústeres)
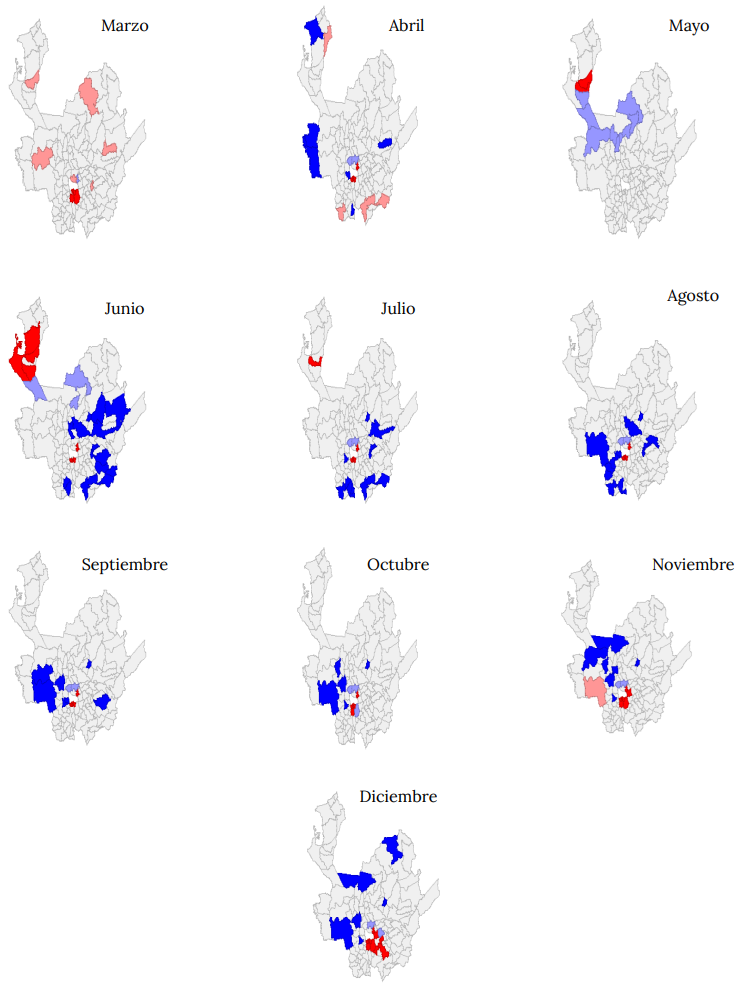
NotaEl clúster HH (alto-alto) municipios en rojo. El clúster LL (bajo-bajo) municipios en azul. El clúster HL (alto-bajo) municipios en rosa. Clúster LH (bajo-alto) municipios en azul claro. Municipios en blanco estadísticamente no significativos.
Fuente: elaboración propia, a partir de datos del Ministerio Nacional de Salud.
Cuadro 7. Moran local para 2021, excluyendo a Medellín (mapa de clústeres)
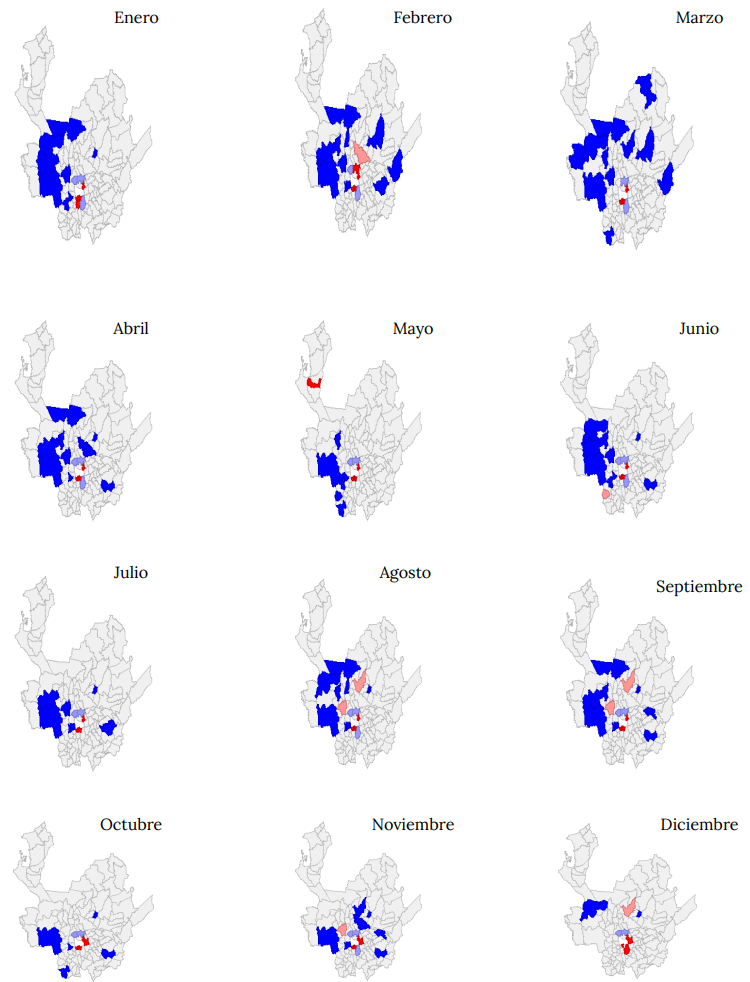
*El clúster HH (alto-alto) municipios en rojo. El clúster LL (bajo-bajo) municipios en azul. El clúster HL (alto-bajo) municipios en rosa. Clúster LH (bajo-alto) municipios en azul claro. Municipios en blanco estadísticamente no significativos.
Fuente: elaboración propia a partir de datos del Ministerio Nacional de Salud.
D. Efecto Spillover Espacial del Covid-19
Con base en las ecuaciones 1 y 2, referidas en la sección metodológica, se calculó el efecto spillover para los modelos Sarma estimados. Tales cálculos, desde el enfoque matricial que implican, permiten el cálculo del efecto para los 125 municipios considerados en la muestra y, por tanto, permite aproximarse a la capacidad de difusión espacial por municipio (ecuación 2). Como se indicó, el objetivo fue establecer el promedio del efecto por fila para la matriz inversa referida en la ecuación 2 y establecer, con ello, el efecto spillover para cada municipio. Este efecto es, además, una aproximación a la capacidad de difusión del virus a nivel municipal.
En la figura 3, se presenta el efecto spillover promedio departamental para cada mes del periodo. Los mayores efectos difusión promedio en el departamento se encuentran, como puede verse, en los meses en los que se dieron los picos de contagio. De hecho, salvando la escala de medida, el comportamiento de la capacidad de difusión espacial del virus es similar a la evolución del número de contagios (figura 1). A partir de julio del 2021, momento del mayor nivel de capacidad de contagio, la capacidad de difusión promedio experimenta una caída sostenida, bajando a 0.02 con respecto al mes de inicio de la pandemia.
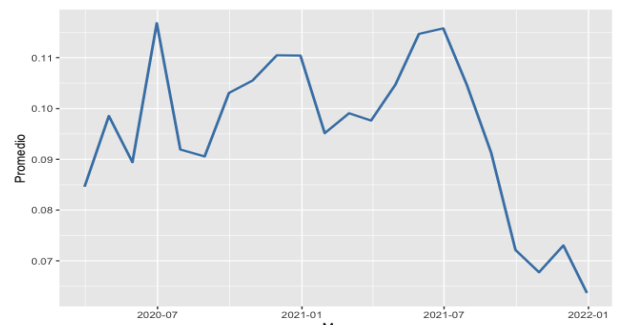
Fuente: elaboración propia a partir de datos del Ministerio Nacional de Salud.
Figura 6. Comportamiento del efecto spillover promedio departamental
Si bien el proceso de vacunación ha avanzado, y mucho de la caída señalada en la capacidad de contagio es consecuencia de esto, con respecto al nivel inicial de la pandemia dicha capacidad de contagio intermunicipal promedio no se ha reducido. Esto, es conveniente advertir, se dio en medio de una nueva ola de contagios que tuvo lugar en diciembre del 2021 por la circulación de una nueva variante denominada “omicrón”, que en el país ha empezado a desplazar la variante “Delta” y ha incrementado los niveles de contagio por ser una variante mucho más transmisible que las anteriores. Lo que muestran los resultados, entonces, es que la vacunación no limitó lo suficiente la capacidad de difusión espacial entre municipios del departamento.
De hecho, el cuadro 9 ilustra la distribución espacial del efecto spillover promedio para cada municipio, comparando el inicio de la pandemia con diciembre de 2021. Esencialmente, el patrón espacial es el mismo en los dos años, por lo que si bien la capacidad de difusión es ligeramente menor en 2021-12, las características en cuanto a ubicación del efecto spillover son las mismas. Esto indica, además, que rebrotes particulares en los municipios más contagiosos regionalmente pueden tener implicaciones importantes en otros municipios, aunque el efecto escala sea menor por la vacunación, pero los niveles de atención médica, así como las condiciones etéreas y socioeconómicas difieren entre municipios, por lo que escenarios de rebrote tienen repercusiones diferenciales. Así, identificar los municipios de mayor capacidad de difusión regional ayudaría a la formulación de políticas y medidas de choque ante nuevos escenarios de riesgo de salud pública.
En tal sentido, en el cuadro 10 se ponen los municipios con mayores capacidades de contagio promedio. De acuerdo con los anteriores resultados, Medellín es el municipio con mayor capacidad de contagio intermunicipal del departamento, seguido de Yolombó y Santa Rosa de Osos. Este ranking revela un aspecto importante: los municipios considerados se distribuyen en siete de las nueve subregiones del departamento, que son las de mayores densidades poblacionales del departamento.
E. Implicaciones en políticas públicas
Los anteriores resultados tienen potenciales implicaciones en términos de informar la formulación de políticas públicas que pretendan mitigar los efectos del Covid-19 y de otros virus o enfermedades de transmisión similar. Estos resultados pueden dividirse en tres procedimientos: (1) un análisis de la distribución espacial de los contagios; (2) un análisis de las implicaciones de la métrica de contagio espacial a nivel municipal —efecto spillover— y la clasificación de los municipios y subregiones en términos de esta información; y (3) un proceso de simulación de escenarios contrastantes de rebrotes focalizados, escenarios de planes de vacunación, entre otros. Todo esto permitiría tener un sistema de información para monitorear el curso de transmisión de un virus en su contexto espacial subregional y analizar sus determinantes socioeconómicos más próximos.
De los clústeres espaciales encontrados en el trabajo, para efectos de formular políticas públicas de mitigación, los tipo alto-alto (municipios en rojo en los mapas de los cuadros 5 y 6) y alto-bajo (municipios en rosa), constituirían un segmento a priorizar debido a que contienen las mayores capacidades de contagio. Sin embargo, sería el primer clúster el que debería atenderse de manera inmediata, con medidas simultáneas, como planes de vacunación y asilamiento social. En el departamento, serían los municipios de Medellín y buena parte del Valle de Aburrá, los cuales concentran la mayor actividad económica del departamento. Sin embargo, como se aprecia en la distribución espacial de este clúster, subregiones como Urabá donde se encuentra la zona portuaria y de acceso al mar, también fue un clúster alto-alto. Focalizar estos clústeres permite concentrar esfuerzos de política, de ahí la importancia de la técnica de estadística espacial aplicada permitiría establecer criterios para la elaboración de cercos epidemiológicos relevantes11.
Cuadro 9. Comparativo de efectos spillover promedio por municipio 2020 frente a 2021
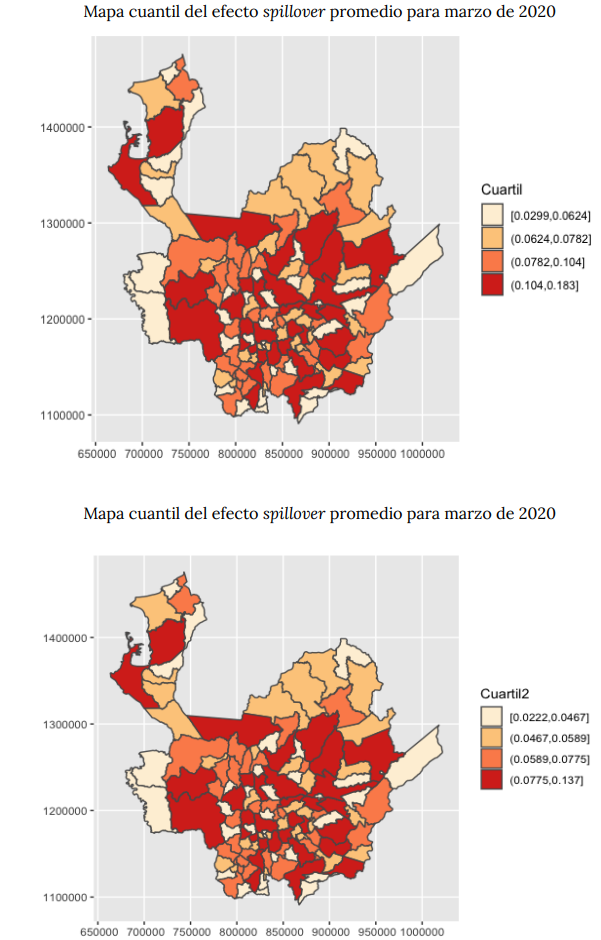
*Los ejes de los mapas corresponden a la proyección cartográfica nacional, equivalente al sistema WGS 48, para norte en el eje vertical y este para el eje horizontal.
Fuente: elaboración propia a partir de datos del Ministerio Nacional de Salud.
Cuadro 10. Ranking de los diez municipios con mayor efecto spillover promedio (2020-3, 2021-12)
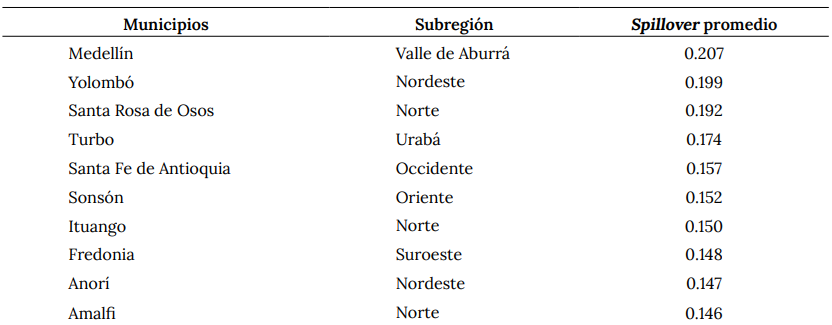
Fuente: elaboración propia a partir de datos del Ministerio Nacional de Salud
El cómputo del nivel de contagio a partir del efecto spillover promedio constituye otra implicación para orientar políticas de mitigación y, además, establecer información que oriente procesos de evaluación de impacto de estas políticas. Por ejemplo, de acuerdo con la figura 3, puede evidenciarse la caída en el efecto spillover espacial que coincide con la ejecución del plan de vacunación en el departamento, este plan condujo a una reducción aproximada de alrededor de un 83 % de la capacidad de contagio promedio del departamento en el pico más alto de transmisión para el mes de Julio de 202112. Disponer, entonces, de esta métrica permite orientar investigación con respecto a determinantes socioeconómicos de la velocidad de contagio subregional, evaluación de impacto de medidas de mitigación y focalización de municipios con mayor capa- cidad de contagio y el curso temporal de estas capacidades. El cuadro 10 permite focalizar estos municipios y ranquear las necesidades de medidas de choque.
Finalmente, el disponer tanto de la señalización de los clústeres espaciales así como el indicador propio de capacidad de contagio, permite establecer escenarios contrastantes simulados respecto a la posible evolución del virus. Así, con la estimación de la ecuación espacial, podrá evaluarse lo que ocurriría si se dieran incrementos hipotéticos de los contagios en un determinado municipio que tiene una cierta capacidad de contagio espacial. Con esta información, puede mantenerse un control y monitoreo constante y una consideración de las implicaciones económicas de la ejecución de medidas alternativas, con la respectiva consideración costo-beneficio.
IV. Conclusiones
En el presente trabajo, se utilizaron herramientas de estadística y econometría espacial para calcular el efecto spillover (efecto de difusión espacial), a fin de determinar el patrón espacial de los contagios del Covid-19 a nivel municipal en Antioquia, desde el inicio de la pandemia hasta diciembre de 2021. A partir de datos globales de contagios a nivel municipal, una vez contrastada la hipótesis de dependencia espacial de estos, el patrón es modelizado mediante modelos Sarma. Luego se estimó el efecto spillover para estos modelos en cada mes y municipio.
Los resultados permitieron evidenciar varios aspectos reseñables: en primer lugar, el municipio con el mayor efecto spillover promedio fue Medellín, desde el inicio, hasta el final del periodo de estudio. Por ser la capital del departamento, es la que concentró los mayores casos de contagio y la que tuvo un mayor factor de contagio espacial sobre otros municipios vecinos. El resultado se explica, por los mayores niveles de interacción interregional de la capital con el resto del departamento. Este sería el curso más factible de propagación del virus hacia el interior de un país, teniendo en cuenta que los mayores niveles de probabilidad de contagio se encuentran en las ciudades principales y estas, a su vez, tienen relaciones con sus ciudades o regiones vecinas. Una evidencia de este resultado es la forma como se configuran los clústeres LISA alto-alto, desde el primer mes de contagio del virus en la capital del departamento; y luego la dispersión de los clústeres alto-alto en las principales subregiones del departamento, como un reflejo de expansión del virus.
En segundo lugar, los resultados evidenciaron también que los mayores niveles de efecto spillover espacial del virus coinciden con los picos de contagio a nivel departamental. De hecho, en junio de 2021, tuvo lugar el mayor pico de contagios del departamento, pero la participación de Medellín, la capital, en el total de casos de contagios fue menor en ese momento al 50 %, por lo que la mayor parte de contagios se encontraban fuera de la capital, lo cual es un reflejo del mayor efecto spillover, ocurrido y la expansión del virus en la mayor parte del departamento.
En tercer lugar, el cómputo agregado del efecto spillover promedio para el departamento sugiere que la capacidad de contagio del virus ha bajado hasta niveles inferiores a la del mes inicial de la pandemia en el departamento. Esto es consecuencia del avance del proceso de vacunación en el país, en el departamento, y en los distintos municipios. Sin embargo, y esto lo capturaron los datos debido que no se actualizan para todo el final de diciembre de 2021 e inicios de 2022, la capacidad de contagio del virus se mantiene a nivel municipal.
Finalmente, en razón a sus condiciones poblacionales y socioeconómicas, la capital del departamento, Medellín, es el municipio con mayor efecto spillover promedio en todo el periodo de estudio, seguido de municipios como Yolombó y Santa Rosa de Osos. De hecho, los municipios con mayor capacidad de contagio se encuentran ubicados en la gran mayoría de las subregiones del departamento, por lo que reducir la capacidad de contagio de estos municipios ayudaría a reducir el nivel de contagios del departamento mismo.
La investigación no se concentró en análisis de los determinantes de los niveles de contagio, objetivo que han tenido otras investigaciones reseñadas aquí y que constituye, para el caso colombiano, un camino relevante en la agenda de investigación por comprender los efectos de la pandemia en distintos niveles. Lo expuesto pone de manifiesto la importancia de considerar el enfoque espacial y regional para el diseño de políticas de salud pública que tengan relación con aspectos económicos. En particular, una agenda de investigación que vincule los datos desagregados por género, edad, etnia, porcentajes secuenciales de vacunación, junto con la inclusión de determinantes de infraestructura hospitalaria y de salud, permitiría una mayor compresión sobre el papel de los determinantes, en aras de disponer de información significativa para potenciales eventos futuros.