^* Este artículo es el resultado de una investigación desarrollada entre enero y noviembre de 2007 por el Grupo de Investigación en Finanzas y Banca (GIFYB) de la Universidad EAFIT, Medellín, Colombia. Financiado por la Dirección de Investigación y Docencia de la Universidad EAFIT. El artículo se recibió el 03-10-2007 y se aprobó el 18-03-2008.

^** Magíster en Finanzas, Universidad EAFIT, Medellín, Colombia (2007); Ingeniero Administrador, Universidad Nacional de Colombia, Medellín, Colombia (2003). Docente investigador, Escuela de Administración, Universidad EAFIT. Miembro del grupo de investigación Finanzas y Banca (GIFYB), Universidad EAFIT. Medellín, Colombia. Correo electrónico: jarbela1@eafit.edu.co

^*** Ph.D. in International Economics and Finance, Brandeis University, Waltham, Massachussets, USA (2004); M.A. in International Economics and Finance, Brandeis University (2000); Especialista en Política Económica, Universidad de Antioquia, Medellín, Colombia (1995); Especialista en Instituciones Financieras, Universidad EAFIT, Medellín, Colombia (1992); Doctor en Leyes, Universidad de Medellín, Medellín, Colombia (1990). Docente e investigadora, Departamento de Finanzas, Universidad EAFIT. Miembro del grupo de investigación Finanzas y Banca (GIFYB), Universidad EAFIT. Medellín, Colombia. Correo electrónico: cmaya@eafit.edu.co

RESUMEN

Este artículo presenta un modelo de valoración de Credit Default Swaps (CDS) sobre bonos corporativos colombianos con base en modelos de riesgo crediticio de forma reducida y el método de simulación de Monte Carlo donde el activo subyacente sigue un proceso estocástico Stopped Poisson. Este modelo es una alternativa interesante para la valoración de CDS en países donde el mercado de bonos corporativos presenta baja liquidez y el mercado de derivados de crédito es incipiente o inexistente, como el caso de Colombia. En su aplicación se obtienen muy buenos resultados para CDS sobre títulos en grado de inversión aunque tiende a sobrevalorar las primas para aquellos títulos que se encuentran en el último nivel de grado de especulación. Por otro lado, se concluye que la sensibilidad de las primas de los CDS es alta respecto a la tasa de ocurrencia del evento de crédito y baja respecto a la tasa de recuperación y a la tasa de interés. Estos resultados confirman aquellos obtenidos en otros estudios empíricos realizados en países con un mercado de derivados de crédito desarrollado.

Palabras clave: derivados de crédito, Monte Carlo, CDS, riesgo de crédito.

ABSTRACT

This article presents a Credit Default Swap (CDS) assessment model for Colombian corporate bonds, based on reduced credit risk models and on the Monte Carlo simulation method where the underlying asset follows a stochastic Stopped Poisson process. This model is an interesting alternative for CDS assessment in countries where the corporate bond market shows low liquidity and the credit derivative market is incipient or does not exist, which is the case in Colombia. Applying this model leads to good results for CDS for investment-grade securities although it tends to overestimate the premiums on securities in the last level of degree of speculation. Furthermore, the conclusion is drawn that the sensitivity of the CDS premiums is high regarding the credit event occurrence rate and low regarding the recovery rate and the interest rate. Such results confirm those obtained from other empirical studies conducted in countries with a developed credit derivate market.

Key Words: credit derivatives, Monte Carlo, CDS, credit risk.

Introducción

Los derivados de crédito son instrumentos financieros que están diseñados para transferir el riesgo de crédito de un activo o un portafolio de activos subyacentes. Estos son contratos o acuerdos mediante los cuales una parte, compradora de protección, adquiere protección contra el riesgo de crédito de un emisor o grupo de emisores. La contraparte, vendedora de protección, está dispuesta a proporcionar dicha protección respondiendo por las pérdidas derivadas de la ocurrencia de un determinado evento de crédito con la expectativa de obtener ganancias en caso de que tal evento no ocurra.

En un contrato de derivado de crédito es esencial especificar quién es el emisor o grupo de emisores del instrumento subyacente, que se denomina entidad de referencia, cuál es la fecha de vencimiento del contrato, cuál es el evento de crédito que da lugar a la cobertura y la forma de calcular el pago a cargo del vendedor de la protección en caso de ocurrencia del mismo. La International Swaps and Derivatives Association (ISDA en adelante) considera seis posibles eventos de crédito: el no pago; la reestructuración de obligaciones; la aceleración del pago; el repudio o la moratoria; el incumplimiento de las obligaciones, y la quiebra. Este artículo se enfoca exclusivamente en el no pago como único evento de crédito.

Entre los principales derivados de crédito se incluyen los Credit Default Swaps (CDS en adelante) y los Total Return Swaps (gráfica 1A, apéndice). El CDS es un contrato financiero bilateral de acuerdo con el cual un comprador de protección paga una prima fija periódica a un vendedor de protección para cubrirse ante un evento de crédito de una entidad de referencia. Se diferencia del Total Return Swap en el que el cálculo de la prima se basa en los cambios del valor de mercado de un instrumento de crédito específico independiente de si ha ocurrido o no un evento de crédito.

En el mercado de los derivados crediticios en los países emergentes, los instrumentos de mayor participación son los CDS con un 85%, con un crecimiento de 631,5 billones de dólares en el año 2001 a 34.422,8 billones de dólares en el 2006 (gráfica 2A, apéndice). La explicación de la alta participación y crecimiento de los CDS, superior a la de los demás derivados de crédito, parece estar en la existencia de una clara regulación dirigida específicamente a estos contratos que data de 1999 (ISDA, 1999, 2003). Estos productos se ofrecen con plazos de uno a diez años, aunque el segmento más activo se encuentra en el rango de uno a cinco años. La obligación subyacente más común para este tipo de contratos son los bonos corporativos (Ranciere, 2002).

En Colombia no se puede hablar aún de la existencia de un mercado de derivados de crédito, debido a la prohibición legal para la negociación de estos instrumentos en el país.¹

Sin embargo, la Superintendencia Financiera le ha permitido a las instituciones bajo su supervisión contratar derivados de crédito en el exterior en ciertas condiciones.² Adicionalmente, desde el 1 de octubre de 2004 se negocian CDS sobre deuda soberana colombiana en mercados internacionales, con vencimientos que se encuentran en uno, dos, cinco y diez años. En el caso particular de los más líquidos, los CDS soberanos a cinco años, la prima se paga cada semestre y su cotización en el último año ha estado en un rango entre 64,8 y 217,5 respectivamente.

Estos antecedentes abren la puerta para la realización de estudios que contribuyan al desarrollo del mercado de derivados de crédito en el país. Esta investigación se enfoca en los CDS, ya que se puede anticipar que estos instrumentos tengan en Colombia la misma preponderancia que han tenido en el ámbito internacional. Ahora bien, en un mercado que en sus inicios será bastante ilíquido, la recomendación para los potenciales vendedores de protección es ofrecer CDS del tipo Binary o Digital en los cuales se pacta un pago fijo ante un evento de crédito, hecho que evita recurrir a cotizaciones del instrumento de referencia difíciles de obtener en un mercado incipiente. Por esta razón, este artículo explora una metodología de valoración apropiada para un Binary CDS en el cual el evento de crédito sea exclusivamente el no pago de un bono corporativo por parte de la entidad de referencia.

1. Los modelos para la estimación del riesgo crediticio

El valor de un CDS depende del comportamiento del riesgo crediticio del activo subyacente. En la literatura se han desarrollado dos enfoques claramente definidos del riesgo crediticio conocidos como modelos estructurales y modelos de forma reducida.

Los modelos estructurales se basan en la evolución de las variables estructurales de la firma, como el valor de los activos y de la deuda. La idea básica de este tipo de modelos es que una compañía incurrirá en un evento de crédito si el valor de los activos de la firma cae por debajo de una determinada barrera o threshold.

Estos modelos parten del propuesto por Merton (1974), que propone valorar tanto el patrimonio como la deuda de una empresa con base en la teoría de valoración de opciones. El evento de no pago de la deuda se daría si, a su vencimiento, el valor de la misma supera el de los activos de la empresa, por lo cual los socios no ejercerían la opción de reclamar el valor de dichos activos en favor de los acreedores. El mérito de esta propuesta radica en ser la primera aproximación a la modelación del riesgo de crédito; sin embargo, el supuesto de que el incumplimiento en el pago sólo ocurre al vencimiento de la deuda, limita su aplicación en la práctica. Posteriormente, Black y Cox (1976) desarrollan otro modelo estructural en el cual consideran que el even-to de crédito se produce en el momento en que el valor de la firma choca con una barrera exógena (Pu, 2007).

Con posterioridad a estos modelos, conocidos como de primera generación, se han desarrollado otros estudios teóricos para mejorarlos. Entre ellos, cabe mencionar Longstaff y Schwartz (1996), el cual incorpora un comportamiento estocástico de las tasas de interés; otros trabajos incluyen modelos de reversión a la media en los índices de apalancamiento de la firma (Collin-Dufresne y Goldstein, 2001); intercambio entre los beneficios y los costos de quiebra para determinar la estructura de capital óptima de una firma emisora de bonos con cupones donde se modela el valor de un activo a través de la ecuación diferencial parcial de Black y Cox (Leland, 1994); relaciones entre acreedores y accionistas de la empresa mediante teoría de juegos (Fan y Sundaresan, 2000), y procesos de salto-difusión en el valor de la firma para incorporar el riesgo de un evento de crédito (Zhou, 2001).

Por el contrario, los modelos de forma reducida se enfocan en el riesgo de la ocurrencia de un evento de crédito inherente a los precios de los activos financieros que son emitidos por la firma. La modelación de este evento depende directamente de la probabilidad de no pago de cada uno de los instrumentos financieros de la firma, lo que lo convierte en un evento aleatorio en el tiempo. La característica principal de estos modelos es que no explican las razones por las cuales una firma incurre en un evento de crédito, pero sí logran calibrar su probabilidad de ocurrencia directamente a partir de los precios de mercado.

Jarrow-Turnbull (1995) y Duffie-Singleton (1999) son los pioneros en el desarrollo de los modelos de forma reducida. El factor clave en sus modelos es la probabilidad del evento de crédito, aunque existen otros elementos, como la estructura a plazos de tasas de interés, la transición de la calificación de riesgo, la tasa de recuperación y la correlación del evento de crédito cuando se trata de un portafolio o índice de diferentes instrumentos de crédito. En estos modelos se asume la existencia de una variable exógena que genera el evento de crédito, con una probabilidad de ocurrencia mayor que cero en cada intervalo de tiempo. El evento de crédito es considerado como un evento estocástico del tipo Poisson, donde el parámetro de intensidad λ corresponde a la tasa de ocurrencia del mismo.

Jarrow-Turnbull (1995) estudian el caso en el que existe un proceso Poisson con una tasa de probabilidad de la ocurrencia del evento de crédito constante y el pago a que este da lugar es conocido. Su trabajo especifica procesos exógenos para la evolución de la estructura temporal de la tasa libre de riesgo y la tasa del bono corporativo para luego aplicar una metodología de valoración neutral al riesgo. Duffie-Singleton (1999) presentan un modelo similar de forma reducida de un activo sujeto a riesgo de crédito para bonos corporativos y soberanos. Argumentan que el spread que existe entre un bono corporativo y un bono libre de riesgo se debe exclu-sivamente al riesgo de crédito. Aunque este puede deberse también a otros factores tales como el riesgo de liquidez o asuntos impositivos, solo se considera el riesgo de crédito para explicar la diferencia entre las rentabilidades de los bonos.

Jarrow, Lando y Turnbull (1997) asumen un proceso de evento de crédito que sigue una cadena de Markov y estiman los parámetros del proceso a partir de datos observados. El modelo emplea información sobre el historial del evento de crédito y cambios en las calificaciones de riesgo.

Podría mencionarse inclusive un tercer grupo de modelos denominados de información incompleta, los cuales pretenden combinar la intuición económica que explica el riesgo de crédito, característica de los modelos estructurales, con la aplicabilidad empírica de los modelos de forma reducida. Estos modelos se caracterizan por no hacer supuestos acerca de la dinámica de la intensidad del evento de crédito, tal como lo hacen los modelos de forma reducida.

El trabajo de Duffie y Lando (2001) es el más importante de los modelos de información incompleta; su aporte se basa en determinar una distribución para el valor de una firma condicionada a la información que tienen los inversionistas. A partir de esta distribución es posible determinar el parámetro de intensidad del evento de crédito de la firma. Frey & Schimdt (2006) realizan una extensión del trabajo de Duffie y Lando (2001), ellos encuentran que el proceso de valoración de los activos financieros conduce a un problema de filtración no lineal con información incompleta sobre el valor de la firma que puede ser solucionado a partir de una aproximación de cadenas de Markov. Herkommer (2006) extiende el modelo de Duffie & Lando (2001) al incorporar correlaciones para determinar el valor de la empresa y un término de ruido, siendo su principal aporte el suministro de una solución cerrada para la valoración de bonos corporativos. Cabe resaltar que sobre los modelos de información incompleta no se han realizado muchos trabajos empíricos, menos aún con información sobre CDS.

Además de los modelos anteriores, existen algunos que han sido propuestos por la industria para la medición del riesgo de crédito. Este es el caso de la metodología propuesta por JP Morgan, conocida como CreditMetrics, que se basa en determinar la probabilidad de que la calidad del crédito se mueva de un nivel a otro, incluyendo también el evento de no pago en un tiempo de horizonte determinado. Por otro lado, se encuentra el modelo propuesto por KMV, en el cual el proceso del evento de no pago está relacionado con la estructura de capital de la firma y el evento de crédito ocurre cuando el valor de la firma cae por debajo de un nivel crítico (Crouhy et al., 2000).

Con base en los modelos de riesgo de crédito descritos, en la literatura se encuentra un número limitado de estudios relacionados con la valoración de CDS. Estos estudios se caracterizan por que la mayoría de ellos utilizan modelos de forma reducida como los propuestos por Jarrow-Turnbull (1995) y Duffie-Singleton (1999) por la facilidad que ofrecen para su calibración e implementación. En cuanto los modelos estructurales, su aplicación a la predicción de las primas de los CDS no ha tenido mucho éxito debido a múltiples razones, entre otras, diversidad de estructuras de capital, diferencias en los instrumentos en cuanto al pago de cupones, el tipo de garantía, la opción o la obligatoriedad de convertibilidad contemplada en algunos de ellos, y la complejidad de los procesos de bancarrota en las diferentes firmas (Pu, 2007).

2. La valoración de los CDS

El valor del CDS depende del diferencial de los flujos de caja esperados a cargo de cada una de las partes. Por un lado, el vendedor de protección asume las pérdidas generadas por el no pago del instrumento subyacente. Este pago puede hacerse en efectivo o por entrega física. En la liquidación física, el comprador de la protección entrega al vendedor el título y recibe a cambio el valor nominal del título en efectivo. La liquidación en efectivo corresponde al pago de la diferencia entre el valor par y el precio de mercado del título o una suma determinada en el caso del Binary CDS. La dificultad de obtener cotizaciones de mercado para un instrumento respecto al que ha ocurrido un evento de crédito es justamente lo que ha hecho tan populares los Binary CDS, donde la suma a pagar ha sido determinada desde el momento inicial del contrato, por lo general con base en tasas históricas de recuperación.

Por otro lado, el comprador del CDS cancela una prima a cambio de la protección contra el riesgo de crédito. Dicha prima es un pago fijo periódico que se determina de tal forma que al inicio del contrato el valor de mercado del CDS sea cero o, lo que es equivalente, que el swap tenga el mismo valor para ambas partes (figura 1). Para la valoración de este tipo de instrumentos es fundamental la modelación del riesgo de crédito que puede generar pagos a cargo del vendedor del CDS.

El pionero de las aplicaciones para la valoración de CDS fue Duffie (1999), quien realiza una aproximación inicial considerando el valor contingente como la diferencia entre el valor facial del bono y su valor de mercado pagado en el momento en que se produce el evento de crédito. Una crítica que se le hace a este artículo es que no se realiza una prueba del modelo utilizando datos reales.

Posteriormente, Hull y White (2000) proponen una metodología para valorar los CDS cuando el pago por incumplimiento se refiere a una sola entidad de referencia y no existe riesgo de contraparte; además, realizan pruebas de sensibilidad del precio de los CDS ante supuestos en la tasa de recuperación esperada y, en última instancia, aplican esta metodología a datos reales de la compañía Ashland Inc. al cierre de sus negociaciones el 13 de julio de 2000.

De nuevo, Hull y White (2001) extienden el estudio realizado en el 2000 en el sentido de considerar el riesgo de contraparte y la correlación entre el incumplimiento de diferentes corporaciones y entidades soberanas. Las principales conclusiones se refieren a que el impacto del riesgo de contraparte sobre el valor de los CDS es pequeño cuando la correlación entre la contraparte vendedora de protección y la entidad de referencia es cero, y que esta se incrementa cuando la correlación aumenta y la calidad de crédito de la contraparte disminuye.

Houweling y Vorst (2005) desarrollan el primer estudio de carácter empírico de valoración de CDS, el cual consiste en comparar los precios de mercado de los CDS con aquellos arrojados en el modelo que proponen. Para la realización del contraste empírico utilizan una base de datos compuesta por los precios de al menos 10.800 bonos de emitidos por 1600 entidades diferentes. La muestra cubre el período entre el 1 de enero de 1999 y el 10 de enero de 2001. Respecto a los datos correspondientes a los precios de los CDS, se observan aproximadamente 48.098 cotizaciones en CDS correspondientes a 837 entidades de referencia distintas en un período que abarca desde el 1 de mayo de 1999 hasta el 10 de enero de 2001. En su trabajo encuentran que el modelo propuesto trabaja bien para las emisiones con grado de inversión, pero que su aproximación en ambientes con altos retornos es pobre, por tal motivo abren la oportunidad para la realización de otras investigaciones de tipo empírico y para un mayor desarrollo del modelo propuesto.

Walker (2005), basándose en el estudio realizado por Hull y White (2001), trata la valoración de los CDS teniendo en cuenta el riesgo de contraparte, pero a diferencia de estos últimos, desarrolla un modelo de cadenas de Markov que se define en términos de las tasas de transición. En este modelo se introduce la dependencia entre la contraparte y la entidad de referencia mediante las tasas de transición en lugar de las correlaciones entre ellas, para así obtener una fórmula analítica más intuitiva y con la posibilidad de hacer una fácil calibración y uso del modelo.

Entre los estudios más recientes se encuentra el desarrollado por Elizalde (2005), quien se basa en Houweling y Vorst (2005) para aplicar y probar su modelo de valoración de CDS en seis firmas españolas. En la aplicación empírica este autor utiliza datos diarios de precios de bonos y de cotizaciones de CDS de las diferentes firmas en un período comprendido entre abril de 2001 y abril de 2002. Los resultados del estudio dejan ver que las primas resultan ser más volátiles que las encontradas en el mercado; al igual que Houweling y Vorst (2005), el modelo trabaja mejor para aquellas firmas con un bajo riesgo de crédito.

Por último, para la estimación de estos modelos, algunos autores recurren al método Monte Carlo. Entre los principales estudios cabe mencionar los trabajos realizados por Zhou (1997) y Hoogland, Neumann y Vellekoop (2002). Zhou (1997) propone un modelo de tipo estructural donde supone que el valor de una firma sigue un proceso de salto-difusión debido a que una firma puede tener un evento de crédito ante una caída inesperada de su valor. El mismo autor sugiere la valoración de CDS utilizando simulación Monte Carlo, aunque para este caso no realiza ninguna aplicación empírica. Hoogland, Neumann y Vellekoop (2002) se basan en los modelos de riesgo de crédito de forma reducida de Duffie-Singleton (1995) y Jarrow-Turnbull (1997), además utilizan el método Monte Carlo para valorar CDS con base en un proceso estocástico que se caracteriza por realizar un único salto que representa el instante en que ocurre el evento de crédito. Al igual que Zhou (1997), no realizan ninguna aplicación empírica del mismo.

3. Una aproximación con el método Monte Carlo al valor de un Binary CDS en Colombia

En la literatura no se encuentran estudios de valoración de CDS enfocados específicamente en mercados emergentes. Para la valoración de un CDS sobre bonos corporativos en Colombia las limitaciones son grandes. En primer lugar, no existen instrumentos derivados de crédito y el mercado de bonos corporativos tiene baja liquidez, lo que plantea una primera dificultad porque no se tienen series amplias de precios de mercado de los mismos. En el mismo sentido, no sería acertado ofrecer CDS cuyo pago dependa de cotizaciones de mercado del instrumento sobre el que ha ocurrido un evento de crédito, pues ni siquiera aquellos que se encuentran en condiciones normales cotizan con frecuencia. Por ello, lo conveniente sería ofrecer Binary CDS donde el pago a cargo del vendedor de protección sea fijado de antemano. Partiendo de que esta recomendación sea aceptada, la metodología que se propone a continuación valora un CDS sobre bono corporativo colombiano del tipo Binary o Digital, donde el evento de crédito es exclusivamente el no pago.

Por otro lado, para la estimación del riesgo de crédito tampoco existe suficiente información para poder aplicar con satisfacción algún modelo de tipo estructural. Por ello se recurre a modelos de riesgo de crédito de forma reducida, lo cual se justifica además porque estos modelos han probado ser mejores empíricamente para determinar las primas de los CDS. Aún así, se hace la salvedad de que la información requerida para la estimación del modelo, principalmente la probabilidad de incumplimiento y las tasas de recuperación, se ha tomado de fuentes externas por no estar disponibles para Colombia.³

A continuación se propone una metodología de valoración utilizando el método Monte Carlo con base en procesos estocásticos de salto que permiten capturar la discontinuad que genera la ocurrencia del evento de crédito. Siguiendo este método, se simulan diversas trayectorias de precios de bonos corporativos sujetos al riesgo del evento de crédito de no pago durante el período de vigencia del CDS. El modelo de riesgo de crédito que se utiliza se basa en el propuesto por Duffie y Singleton (1999) de acuerdo con el cual el activo está sujeto a un proceso estocástico del tipo Stopped Poisson, caracterizado por no seguir siendo efectivo después del primer salto que se da al producirse el evento de crédito. Inmediatamente después de su ocurrencia, el valor del activo sujeto a este proceso cae a un nivel proporcional a su tasa de recuperación. La ventaja de utilizar la simulación con Monte Carlo es que permite considerar un período de no pago incierto, tal como ocurre en la realidad, mientras que otros modelos numéricos y analíticos que han sido propuestos hacen supuestos sobre estos períodos de no pago.

Considere un mercado con un bono corporativo B cuya dinámica es la siguiente:

Donde dq es un proceso Stopped Poisson que se detiene después del primer salto en el momento t_d, t identifica el tiempo, t_d es el instante en que se produce el evento de crédito, μ es el spread de crédito, es decir, el retorno que ofrece el bono corporativo en exceso de la tasa libre de riesgo, R es la tasa de recuperación del bono corporativo. Se refiere al porcentaje del valor del título que se recupera después de ocurrido el evento de crédito.

En un Binary CDS es una tasa fijada desde el momento en que se emite el CDS.

En el momento del evento de crédito, el salto del precio del bono corporativo es:

B_td=R×B_td–1

La expresión anterior indica que el precio del bono corporativo después de ocurrido el evento de crédito corresponderá a un porcentaje del precio que tenía el título antes de dicho evento.

Del proceso (1) se obtiene:

dB=μBdt+(R-1)Bdq (2)

Aplicando el lema de Ito (Ver prueba 1A), se obtiene:

B_t=B₀×e^μdt×e^1n(R)dq (3)

Bajo el supuesto de valoración neutral al riesgo, se tiene que μ=0, por tanto el proceso que se utiliza en la simulación con Monte Carlo es:

B_t=B₀×e^1n(R)Dummy (4)

Donde R tasa de recuperación, λ parámetro de intensidad de no pago

En particular, para valorar un CDS se pro-pone la siguiente metodología basada en la aplicación del método Monte Carlo:

1. Sea B el valor par de un bono corporativo subyacente al CDS que sigue el proceso descrito en (1).

2. Sea t_d el momento en el cual se produce el evento de crédito y T el vencimiento del CDS.

3. Con el método Monte Carlo se generan diversas trayectorias para modelar t_d. En el momento en que se produce el evento de crédito, el proceso termina (Stopped Poisson o Jump Stop) en la trayectoria correspondiente.

4. En cada escenario simulado, si t_d ≤ T, el valor del bono cae a:

R×Valor Par del bono

R:Tasa de recuperación del bono corporativo Valor Par del bono = 1

5. El vendedor de la protección deberá realizar, en el momento en que se produce el evento de crédito, el siguiente pago:

(1-R)×Valor Par del bono

6. Finalmente, se determina la prima del CDS de tal forma que:

El valor presente de los pagos en aquellas trayectorias donde ocurre el evento de crédito se calcula descontando dicho pago a la tasa libre de riesgo, bajo el supuesto de valoración de riesgo neutral.⁴ Este valor debe ser igual al valor presente de los pagos por concepto de prima periódica del CDS, para que el valor del swap sea cero en el momento cero. Luego el pago periódico de la prima en puntos básicos corresponde a la anualidad calculada a partir del valor presente de los pagos realizados por el evento de crédito, el tiempo estipulado para el CDS y la periodicidad pactada para el pago de la prima.

Para aplicar este método de valoración de CDS se requiere información sobre la tasa de recuperación del bono corporativo, pactada desde el comienzo en un Binary CDS, y sobre la probabilidad de la ocurrencia del evento de crédito medida por el parámetro de intensidad λ del proceso Stopped Poisson. El pago de un Binary CDS generalmente se basa en las tasas de recuperación R históricas, información no disponible en el caso colombiano. Una alternativa para fijarla es recurrir a información internacional disponible de bonos corporativos de características similares y es la vía empleada para la aplicación de la metodología propuesta.

En cuanto a la probabilidad de ocurrencia del evento de crédito, la literatura sugiere recurrir a procesos tipo Vasicek o Cox-Ingersoll-Ross (CIR) o estimar el parámetro de intensidad λ a partir de los precios de los bonos corporativos. La probabilidad instantánea de que se produzca el evento de crédito entre un período y el siguiente será igual a λdt. Sin embargo, para el caso de los mercados emergentes existe una gran dificultad para la aplicación de cualquiera de estas dos metodologías en la estimación de dicho parámetro debido a la baja liquidez del mercado de los bonos corporativos, que se traduce en información insuficiente.

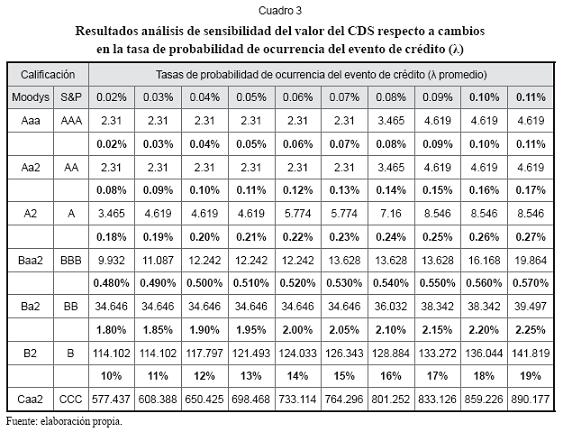
Por lo anterior, para la aplicación propuesta la probabilidad del evento de crédito se considera constante y es estimada a partir de información histórica disponible en mercados desarrollados por las firmas calificadoras Moody’s Investors Service y Standard & Poors (S&P). En el cuadro 1A (ver apéndice) se presentan las tasas de ocurrencia del evento de crédito que han sido calculadas por estas firmas para diferentes calificaciones de bonos corporativos sobre los cuales se han emitido CDS a un plazo de cinco años (ver cuadro 2A en el apéndice para las equivalencias de calificaciones). Por último, se asume que la calificación del título permanece constante durante todo el período pactado para el CDS, en concordancia con la mayoría de los estudios revisados con excepción de Walker (2005).

El modelo propuesto se calibra con el de Hull y White (2000) donde se estima el valor de un CDS con vencimiento de cinco años, siendo la tasa libre de riesgo igual al 5% anual compuesto continua,⁵ la tasa de recuperación R es de 40% y λ es igual a 0,02. El resultado que se obtiene en la valoración utilizando simulación con Monte Carlo es plenamente satisfactorio, ya que el valor estimado es de 124 puntos básicos para la prima del CDS, igual al obtenido por Hull y White, como se muestra en el cuadro 1.

Luego de garantizarse una buena calibración del modelo, se procede a realizar su aplicación al caso colombiano con base en la información limitada que se tiene, de acuerdo con lo explicado previamente. Para realizar diferentes estimaciones del valor de un potencial Binary CDS sobre un bono corporativo de un emisor colombiano se utilizan las tasas de ocurrencia del evento de crédito (λ) del cuadro 1A, las tasas de recuperación estimadas por Moody’s⁶ que se muestran en el cuadro 3A⁷ y se asume un vencimiento de cinco años.⁸ Sin embargo, desde el punto de vista de un inversionista internacional, debido a que un título de estos tiene implícito un riesgo crediticio del país al cual pertenece, se propone adicionar a este resultado los puntos correspondientes a la cotización de CDS soberanos para Colombia en los mercados internacionales. Los resultados se muestran en el cuadro 2 donde el valor de la prima será menor en la medida en que la calificación y las garantías de la emisión sean mejores.

Al comparar los resultados obtenidos utilizando el modelo propuesto con primas del mercado, se observa que las emisiones de CDS con muy buena calificación crediticia tienen primas muy similares, como las calificaciones Aa y Baa. Sin embargo, a medida que la calificación del CDS es más baja, el modelo tiende a sobreestimar las primas, como ocurre con aquellos títulos con calificaciones B y Caa. Estos resultados concuerdan con los obtenidos por Houweling y Vorst (2005) y Elizalde (2005).

El mismo proceso de valoración se realiza para diferentes tasas de recuperación con el fin de observar la sensibilidad de las primas de los CDS ante variaciones en las tasas de recuperación de los bonos (cuadro 4A), los resultados obtenidos se observan en el gráfico 1. Con excepción de los títulos de muy baja calidad crediticia, el valor de las primas de los CDS es poco sensible a cambios en la tasa de recuperación del título. Lo anterior confirma los resultados obtenidos en otros estudios empíricos. Además, se realizó un análisis de sensibilidad respecto a la tasa de interés (cuadro 5A), también se concluye que hay una baja sensibilidad de la prima del CDS a cambios en la tasa de interés.

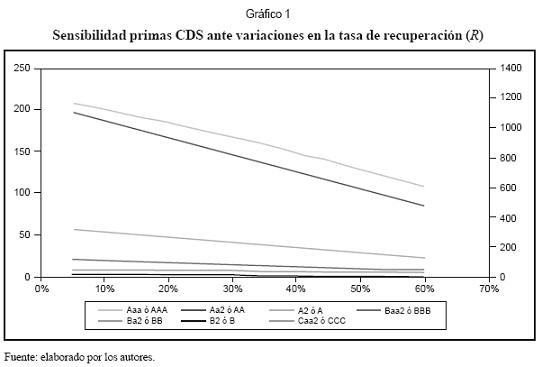
Por el contrario, ante variaciones en un rango de aproximadamente 0,1% alrededor de la mediana de la tasa de ocurrencia del evento de crédito, la prima de los CDS sobre bonos tipo Aaa-A2 prácticamente se duplica, aunque en valores absolutos el cambio no es muy significativo por el bajo costo de estos CDS. Para los títulos con calificación Baa2-Ba2, la prima se incrementa ante variaciones de igual magnitud, pero no en la misma proporción que para los de alta calificación. Finalmente, para los títulos de muy baja calificación (B2-Caa2), la prima se observa poco sensible, probablemente por el hecho de que la tasa de ocurrencia del evento de crédito ya es bastante alta así como el valor del CDS. Estos resultados se muestran en el cuadro 3.

En el gráfico 2 se muestran los resultados obtenidos para CDS que se podrían ofrecer sobre bonos corporativos colombianos. Cabe recordar que la estimación de estos valores se realiza añadiendo los puntos del CDS soberano de Colombia a las estimaciones realizadas en el cuadro 2. Para realizar esta estimación se utilizaron datos históricos de las cotizaciones de CDS de Colombia a cinco años, desde el 1 de agosto de 2006 hasta el 31 de julio de 2007.⁹

Como puede observarse, en promedio las primas de CDS sobre bonos corporativos de Colombia con calificaciones Aaa y Aa se encontrarían durante el período de estudio alrededor de 111 puntos básicos y nunca sobrepasan los 200 puntos básicos. Para el caso de los CDS sobre bonos tipo A, su valoración se encontraría en promedio alrededor de los 114 puntos básicos, mientras que para los Baa sería en promedio de 141 puntos básicos.

Conclusiones

En Colombia, los inversionistas son reacios a invertir en bonos y otros títulos cuya calificación de riesgo no se encuentre en los niveles más altos de calidad crediticia. La razón principal se debe a que, tal como lo expresa BRC Investor Services (1996), falta conocimiento y capacitación por parte de la comunidad empresarial y financiera del país en la utilización de nuevos mecanismos de cobertura eficientes como los derivados de crédito.

Podría pensarse que en Colombia no es viable tener un mercado de derivados de crédito debido al pequeño tamaño y a la baja liquidez del mercado de bonos corporativos. Sin embargo, como en otros países emergentes, los mercados de derivados de crédito y los de bonos crecen en forma conjunta dinamizándose mutuamente. Del mismo modo, en el país existe un creciente interés por incrementar la participación de las empresas en el mercado de capitales, y la existencia de instrumentos como los derivados de crédito promoverían dicha participación.

Este artículo se constituye en una primera aproximación a la valoración de derivados de crédito, específicamente CDS, para que tanto inversionistas como futuros proveedores de estos instrumentos derivados en el país tengan herramientas para medir el riesgo de crédito al cual se exponen, o el que están cubriendo, ante las limitaciones de información existentes. Modelos de valoración como el presentado aquí contribuirán a desatar el nudo gordiano que existe en el país, que consiste en que no existe liquidez de bonos corporativos porque no hay instrumentos de cobertura, y no es posible desarrollar instrumentos de cobertura debido a la baja liquidez del mercado de bonos corporativos.

En un mercado que en sus inicios será bastante ilíquido, la recomendación para los potenciales vendedores de protección es ofrecer CDS del tipo Binary o Digital en los cuales se pacta un pago fijo ante un evento de crédito, esto evita recurrir a cotizaciones del instrumento de referencia difíciles de obtener en un mercado incipiente y facilita la valoración de tales instrumentos.

Para el caso de Colombia, además se hace necesario la escogencia de modelos de forma reducida y el uso de Simulación tipo Monte Carlo, debido a que los primeros se convierten en herramientas útiles cuando no existe suficiente información del mercado, como ocurre en los mercados emergentes o cuando los supuestos de los modelos analíticos existentes son muy fuertes, de manera que una aproximación numérica tendría más sentido. La ventaja de utilizar simulación Monte Carlo es que permite considerar un período de no pago incierto, como ocurre en la realidad, mientras que otros modelos analíticos que han sido propuestos hacen supuestos sobre estos períodos de no pago.

El modelo propuesto aquí obtiene muy buenos resultados en títulos que se encuentran en grado de inversión y tiende a sobrevalorar las primas para aquellos títulos que se encuentran en el último nivel de grado de especulación. Por otro lado, se concluye que la sensibilidad de las primas de los CDS es alta con respecto a la tasa de ocurrencia del evento de crédito y baja con respecto a la tasa de recuperación y a la tasa de interés.

Estos resultados confirman los obtenidos en otros estudios empíricos realizados en países con un mercado de derivados de crédito desarrollado.

En la valoración de CDS, el parámetro más importante corresponde a las probabilidades de ocurrencia del evento de crédito de cada título en particular. En este caso, se utilizaron estándares internacionales; sin embargo, en el futuro, cuando el mercado de bonos corporativos presente más liquidez y exista un número suficiente de datos, la estimación de este y de los demás parámetros del modelo se podrá hacer para cada entidad en particular.

Notas al pie de página

1. Circular Reglamentaria Externa DODM 144 de 2006 del Banco de la República de Colombia: “Los contratos de derivados financieros autorizados […] se refieren exclusivamente a riesgos de derivados de tasa de cambio, tasa de interés e índices bursátiles. En las operaciones permitidas se pueden incluir cláusulas referidas a eventos crediticios, siempre y cuando se trate del riesgo de cualquiera de las partes del contrato. Los contratos de derivados de crédito no están autorizados” (Banco de la República, 2006)

2. La Circular Externa 013 de junio de 2006 de la Superintendencia Financiera de Colombia, capítulo XVIII, establece: “Las entidades que muestren al ente supervisor un adecuado conocimiento de los riesgos potencial es del uso de derivados de crédito […], podrán utilizar los derivados de crédito para mitigar su exposición al riesgo de crédito. En consecuencia, los derivados de crédito se podrán usar para transferir este riesgo a un tercero que resida en el exterior y con el cual la entidad que los realiza no tenga ningún vínculo de consolidación o que pertenezca al mismo grupo económico o holding” (Superfinanciera, 2006).

3. Si el evento de crédito a considerar es cambios en la calificación de la obligación, BRC Investor´s Services ha calculado matrices de transición útiles para la estimación del riesgo crediticio.

4. Los bonos son instrumentos negociables sobre los cuales no existe una prohibición expresa de ventas en corto, por tanto, es posible conformar un portafolio que permita la utilización de un método de valoración neutral al riesgo.

5. En esta y en las siguientes estimaciones se asume una estructura plana de las tasas de interés que no afecta el resultado, pues el valor de los CDS es muy poco sensible a cambios en la tasa de interés, como se muestra en el cuadro 5A.

6. Estas tasas de recuperación y de no pago corresponden a bonos corporativos de una muestra amplia de diferentes países.

7. Se supone que con base en información histórica de tasas de recuperación es que se pacta el pago fijo a cargo del vendedor de protección en un Binary CDS.

8. Estos son los CDS más líquidos en el mercado de derivados de crédito en el mundo.

9. Información obtenida en la plataforma Bloomberg.

Lista de referencias

1. Altman, E. and G. Fanjul (2004). Defaults and returns in the high yield bond market: analysis through 2003. Working Paper.         [ Links ]

2. Anson, M. et al. (2004). Credit derivatives, instruments, applications and pricing. New York: Wiley Finance, 341 p.         [ Links ]

3. Asobancaria (2006). Los derivados de crédito: una excelente herramienta para la mitigación del riesgo. La semana económica, 1(542): 1-4.         [ Links ]

4. Banco de la República de Colombia (2006). Circular reglamentaria externa DODM 144 de 2006. Recuperado el 15 de Marzo de 2007, de http:// quimbaya.banrep.gov.co/documentos/reglamentacion/pdf/CRE-DODM-144mayo06.pdf         [ Links ]

5. Black, F, and J, Cox (1976). Valuing corporate securities: some effects of bond indenture provisions. Journal of Finance, 31(1): 351-367.         [ Links ]

6. BRC Investor Services (1996). Derivados de crédito. Notas del mercado de capitales. 1(2).         [ Links ]

7. BRC Investor Services (2007). Calificaciones de deuda a largo plazo. Recuperado el 18 de febrero de 2008, de http://www.brc.com.co/inicio.php?Id_Categoria=198        [ Links ]

8. Collin-Dufresne, P., Goldstein, R. S. and J, Martin (2001). The determinants of credit spread changes. Journal of Finance, 56(1): 77-207.         [ Links ]

9. Crouhy, M. et al. (2000). A comparative analysis of credit risk models. Journal of Banking and Finance, 24(1): 59-117.         [ Links ]

10. Deutsche Bank Research (2003). Credit derivatives: Implications for credit markets. Recuperado el 18 mayo de 2007, de http://www.dbresearch.de/PROD/DBR_INTERNET_DEPROD/PROD0000000000060515.pdf        [ Links ]

11. Dufey, G and F. Rehm (2000). An introduction to credit derivatives. Michigan: University of Michigan. Working Paper, 9 p.         [ Links ]

12. Duffie, D. (1999). Credit swap valuation. Financial Analysts Journal, 55(1): 73-85.         [ Links ]

13. Duffie, D. and D. Lando, (2001). Term structure of credit spreads with incomplete accounting information. Econometrica, 69(1): 633-664.         [ Links ]

14. Duffie, D. and K. Singleton (1999). Modeling term structures of defaultable bonds. Review of Financial Studies, 12(1): 687-720.         [ Links ]

15. Elizalde, A. (2005). Credit default swap valuation: an application to spanish firms. Working Paper. Madrid: CEMFI and UPNA, 39 p.         [ Links ]

16. Fan, H., and S, Sundaresan (2000). Debt valuation, renegotiation, and optimal dividend policy. Review of Financial Studies, 13(1): 1057-1099.         [ Links ]

17. Frey, R. and T, Schmidt (2006). Pricing corporate securities under noisy asset Information. Working Paper. Leipzig: University of Leipzig, 18 p.         [ Links ]

18. Herkommer, D. (2006). Correlation effects in credit risk models with incomplete accounting information. Working Paper. Mertonstr: Goethe University, 36 p.         [ Links ]

19. Hoogland, J, Neumann, D and M. Vellekoop (2002). Symmetries in jump-diffusion models with applications in option pricing and credit risk. International Journal of Theoretical and Applied Finance, 6(2): 135-172.         [ Links ]

20. Houweling, P., and A, Vorst (2005). Pricing Default Swaps: Empirical Evidence. Journal of International Money and Finance, 24(1): 1200-1225.         [ Links ]

21. Hull, J. (2006). Options Futures and Other Derivatives. Toronto: Prentice Hall.         [ Links ]

22. Hull, J., andA, White (2000). Valuing Credit Default Swaps I: No Counterparty Default Risk. Journal of Derivatives, 8(1): 29-40.         [ Links ]

23. Hull, J., and A, White (2001). Valuing Credit Default Swaps II: Modeling Default Correlations. Journal of Derivatives, 8(3): 12-22.         [ Links ]

24. ISDA (1999). 1999 ISDA Credit Derivatives Definitions. Recuperado el 24 de marzo de 2007, de http://www.isda.org/publications/isdacreditderi-def-sup-comm.html         [ Links ]

25. ISDA (2003). 2003 ISDA Credit Derivatives Definitions. Recuperado el 24 de marzo de 2007, de http://www.isda.org/publications/isdacreditderi-def-sup-comm.html#isdacrd        [ Links ]

26. Jarrow, R. A. and S, Turnbull (1995). Pricing derivatives with credit risk. Journal of Finance, 50(1): 53-85.         [ Links ]

27. Jarrow, R. A., Lando, D. and Turnbull S. (1997). A Markov model for the term structure of credit spreads. Review of Financial Studies, 10(2): 481-523.         [ Links ]

28. Leland, H. (1994). Risky debt, bond covenants and optimal capital structure. Journal of Finance, 49(1): 1213-1252.         [ Links ]

29. Longstaff, F., and E, Schwartz (1996). A simple approach to valuing risky fixed and floating rate debt. Journal of Finance, 50(1): 789-821.         [ Links ]

30. Merton, R. C. (1974). On the Pricing of Corporate Debt: The Risk Structure of Interest Rates. Journal of Finance, 29(2): 449-469.         [ Links ]

31. Moody´s Investors Services (2004). Historical Default rates of Corporate Bond Issuers, 1973-2003. Recuperado el 20 de junio de 2007, de http://www.moodys.com        [ Links ]

32. Pu, X. (1997). A survey on credit default swap valuation. Working Paper. Massachusetts: University of Massachusetts, 42 p.         [ Links ]

33. Ranciere, R. (2002). Credit Derivatives in Emerging Markets. Working Paper. New York: International Monetary Fund, 24 p.         [ Links ]

34. Superintendencia Financiera de Colombia (2006). Valoración, contabilización y manejo de riesgos de operaciones con productos derivados. Circular Externa 013, 35 p.         [ Links ]

35. Walker, M. (2005). Credit default swaps with counterparty risk: a calibrated markov model. Working paper. Toronto: University of Toronto, 19 p.         [ Links ]

36. Zhou, C. (1997). A jump-diffusion approach to modelling credit risk and valuing defaultable securities. Washington D.C.: Federal Reserve Board, 49 p.         [ Links ]

37. Zhou, C. (2001). The Term Structure of Credit Spreads with Jump Risk. Journal of Banking and Finance, 25(1): 2015-2040.         [ Links ]