Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Administración
Print version ISSN 0120-3592
Cuad. Adm. vol.27 no.48 Bogotá Jan./June 2014
¿Los índices de mercado son carteras eficientes? El caso español del IBEX-35*
Are the market indexes efficient portfolios? The Spanish case of IBEX-35
Os índices de mercado são carteiras eficientes? O caso espanhol do IBEX-35
Mariano González Sánchez**
JuanM. Nave Pineda***
*Este trabajo es financiado por el proyecto de investigación ECO 2012-36685 del Ministerio de Economía y Competitividad de España. Se encuentra en desarrollo desde el 1 enero de 2012 y se espera su finalización el 31 de diciembre de 2015. El artículo se recibió el 20-12-13 y se aprobó el 08-04-14. Sugerencia de citación: González S., M. y Nave P., J. M. (2014). ¿Los índices de mercado son carteras eficientes? El caso español del IBEX-35. Cuadernos de Administración, 27 (48), 183-226.
**Doctor en Ciencias económicas y empresariales, Universidad Ceu San Pablo, Madrid, España, 1998; Licenciado en ciencias empresariales, Universidad Complutense, Madrid, España. Profesor adjunto, Universidad CEU Cardenal Herrera, Madrid, España. Correo electrónico: mariano.gonzalez@uch.ceu.es
***Doctor en Ciencias económicas y empresariales, Universidad de Valencia, Valencia, España, 1996; Licenciado en ciencias empresariales, Universidad de Valencia, Valencia, España, 1990. Profesor titular, Universidad de Castilla de la Mancha, Cuenca, España. Correo electrónico: JuanNave@uclm.es
Resumen
En la práctica financiera de gestión y valoración de activos suele emplearse como cartera eficiente de mercado su índice representativo. En la literatura financiera los estudios empíricos para contrastar si el índice de mercado es una cartera eficiente suelen asumir únicamente un comportamiento gaussiano (media-varianza). Por el contrario, en este trabajo se propone una metodología tanto en entorno gaussiano como no gaussiano, así como pruebas del tipo backtesting para considerar a posteriori los errores tipo-I y II. Los resultados de aplicar la metodología propuesta sobre el índice del mercado español (IBEX-35) muestran que pueden encontrarse carteras óptimas más eficientes que el IBEX-35 y con un menor número de activos. Además, bajo un entorno no gaussiano se superan los test y, no se presenta el problema habitual de primas de riesgo de mercado no positivas.
Palabras clave: Cartera de mercado, índice de mercado, optimización.
Clasificación JEL: G11, G12.
Abstract
In financial management and asset pricing is often used the market as the efficient market portfolio. The empirical studies to test the efficiency of market index usually assume a gaussian behavior (mean-variance). By contrast, this paper proposed a backtesting methodology from the post type-I and II errors, for both gaussian and non-gaussian behavior. The results on Spanish market index (IBEX-35) show that optimal portfolios may be more efficient than the IBEX-35 with fewer assets, which under a non-Gaussian test are exceeded and, without exhibiting the usual problem of market risk premiums not positive.
Keywords: Market portfolio, market index, optimization.
JEL Classification: G11, G12.
Resumo
Na prática financeira de gestão e valoração de ativos, costuma empregar-se como carteira eficiente de mercado seu índice representativo. Na literatura financeira, os estudos empíricos para contrastar se o índice de mercado é uma carteira eficiente, costumam assumir unicamente um comportamento gaussiano (média-variância). Pelo contrário, neste trabalho propõe-se uma metodologia tanto em contexto gaussiano quanto não gaussiano, bem como provas do tipo backtesting para considerar a posteriori os erros tipo-I e II. Os resultados de aplicar a metodologia proposta sobre o índice do mercado espanhol (IBEX-35) mostram que se podem encontrar carteiras mais eficientes que o IBEX-35 e com um menor número de ativos. Além disso, sob um contexto não gaussiano, superam-se os testes e não se apresenta o problema habitual de prémios de riscos de mercado não positivas
Palavras chave: Carteira de mercado, índice de mercado, otimização.
JEL Classificação: G11, G12.
Introducción
Los índices del mercado de renta variable son habitualmente empleados en la práctica financiera como referencia en la gestión de carteras y la valoración de activos. Ello supone implícitamente que dichos índices son una proxy de la llamada cartera de mercado, definida como la de mayor rendimiento por unidad de riesgo.
Ahora bien, la denominada crítica de Roll (1977) sobre la contestación de la Teoría de Valoración de Activos (Capital Asset Pricing Model: CAPM) exige conocer la cartera de mercado y que para su construcción sean considerados todos los activos del mercado. De este modo, sustituir dicha cartera por una proxy, un índice de mercado, no sólo no permite contrastar la validez de la teoría, sino que podrían cometerse errores en la estimación del riesgo de mercado, es decir, cualquier gestión o valoración de activos asociada a un índice no contrastado como cartera eficiente podría conllevar una infra o sobre valoración del riesgo.
Surge entonces la cuestión sobre la validez de la construcción de los índices de mercado como carteras eficientes, es decir, ¿las ponderaciones asignadas a los diferentes activos son adecuados para construir una buena proxy de la cartera de mercado?
En este contexto, el objetivo principal de este trabajo es determinar si a priori el IBEX-35 (índice del mercado continuo español) es una cartera óptima, es decir, si es posible encontrar otras ponderaciones para los mismos 35 valores que ofrezcan una mayor rentabilidad por unidad de riesgo. Por tanto, el objetivo no es "batir" al IBEX-35, sino proporcionar a los agentes económicos una validación de este índice como cartera de mercado.
Realizamos este estudio bajo dos entornos: por un lado, consideramos un comportamiento gaussiano del rendimiento de los activos (media-varianza), tal y como se desprende de la CAPM; y por otro, incluimos momentos muestrales de orden mayor a 2 (asimetría y curtosis). Para este último supuesto, la performance de las carteras vendrá dada en términos de media frente al Value at Risk. Finalmente, para contrastar si los resultados a priori se mantienen al final del período de inversión, y dado que consideramos tanto un comportamiento normal como no normal, recurriremos a pruebas de backtesting.
Para este estudio se empleará una muestra comprendida entre enero-2000 y marzo-2013 de los precios de las acciones que forman parte del IBEX-35 en cada instante temporal.
El resto del trabajo se organiza así: en el segundo apartado se hace un repaso de la literatura que ha tratado el mismo tema desde otras perspectivas; en el tercero se exponen las metodologías seguidas para estimar los pesos de las carteras óptimas; en el cuarto explicamos la selección de la muestra y sus características estadísticas, en el quinto presentamos los resultados y, finalizamos con las principales conclusiones.
1. Revisión de la literatura
Existen numerosos trabajos que analizan la validez de la CAPM, cabe destacar al respecto DeMiguel et al. (2009), que comprueban, en un entorno gaussiano (ratio de Sharpe) si las estrategias habituales de optimización superan el rendimiento obtenido por una cartera equiponderada. Los resultados indican que el problema estriba en el error de estimación de los momentos muestrales, es decir, serían necesarios muchos más datos para que el resultado de la optimización superase a la equiponderada. Otro trabajo reseñable es Levy y Roll (2010), donde se pone de manifiesto que pequeñas variaciones en los parámetros muestrales de media y varianza (entorno gaussiano) pueden hacer que las carteras proxy de mercado sean eficientes, concluyendo entonces que el modelo CAPM no puede ser rechazado. A partir de estos trabajos queda en evidencia que bajo un comportamiento gaussiano (media y varianza) los momentos muestrales presentan problemas.
En la literatura financiera también existen trabajos con un objetivo de contraste similar, pero sobre diferentes mercados, por ejemplo Arcos et al. (2010) emplean diferentes métodos de estimación de carteras óptimas en entorno gaussiano para Latinoamérica. Pero en estos casos también se observa que los estadísticos descriptivos de las muestras no parecen corresponder a un comportamiento normal.
El interés que ha recibido este tema se refleja en las numerosas publicaciones que analizan el estado de la materia; por ejemplo Lewellen et al. (2010), Brown y Walter (2013), Cantillo (2013), Campbell (2014) y Schlegel (2014).
Para el caso español, la mayoría de estudios empíricos se centran en la posibilidad de obtener rendimientos sistemáticamente superiores a la cartera de mercado. Hay dos aspectos en base a los que podemos clasificar estos trabajos: por un lado la estrategia seguida para seleccionar carteras que puedan generar rendimientos superiores al mercado (v.gr. activos infravalorados, fondos de inversión), y por otro, la técnica estadística empleada para medir si el rendimiento obtenido es sistemáticamente mayor que el del mercado (Ferruz y Sarto, 1993; Gómez-Bezares et al., 1996; Méndez y Álvarez, 2000; Jordán y García, 2002; Gómez-Bezares et al., 2012). Ahora bien, en todos los casos se asume que la cartera de mercado es el IBEX-35 o el IGBM (Índice General de la Bolsa de Madrid), de manera que cualquier conclusión estaría sesgada en términos de la CAPM, por cuanto dichos índices podrían no ser una buena proxy a priori de la cartera de mercado.
Otra línea de investigación sobre el mercado español está compuesta por trabajos que, o bien han incorporado más factores explicativos, como el caso multi-beta (Nieto y Rubio, 2002); o bien, han simplificado el problema de optimización de carteras (Villalba, 1998), empleando medidas del riesgo sustitutivas de las covarianzas, como las desviaciones medias absolutas, transformando así el problema cuadrático en lineal. En cualquier caso, el objetivo de estos trabajos tampoco fue contrastar la validez de las ponderaciones del IBEX-35. Esta cuestión tampoco es considerada por Gómez-Sala y Marhuenda (1998), cuando construyen dos índices equiponderado y ponderado por capitalización, para contrastar las anomalías del mercado y la validez de la CAPM en el caso español, siendo su principal conclusión el poder explicativo del tamaño que -recordemos- está incluido en la construcción de carteras o índices por capitalización.
El primer precedente de este trabajo es Rubio (1986), aunque dicha investigación no busca una cartera óptima, sino que analiza en qué medida un índice del mercado español puede ser una proxy adecuada de la cartera de mercado, expresado en términos de correlación lineal entre ambas carteras, por tanto en un entorno gaussiano. De igual modo ocurre con Torre (2013), que a través de un test sobre una variable dicotómica que compara el ratio de Sharpe (entorno gaussiano) del índice con otras dos carteras, una resultado de optimizar los datos históricos de los activos; y otra, los datos simulados por muestreo con remplazamiento, llegan a resultados contradictorios: en el primer caso se acepta que el índice es eficiente y en el segundo no.
Así pues, resulta reiterativo el problema del entorno gaussiano, puesto de manifiesto en los parámetros y en la estadística descriptiva de las series. Además, la literatura financiera para el caso español adolece de un estudio empírico sobre la validez de los pesos del IBEX-35 como representativos a priori de los de la cartera de mercado bajo un comportamiento no gaussiano, todo lo cual justifica este trabajo.
2. Metodología
2.1. Hipótesis generales de la CAPM
Para contrastar si el índice del mercado es una buena proxy ex ante de la cartera de mercado, asumimos inicialmente las hipótesis del modelo CAPM:
- Modelo estático: consideramos que los inversores invierten al inicio del período y el consumo se realiza al final del período de inversión. Esto lo realizaremos en fechas consecutivas y sin posibilidad de operaciones entre ellas.
- Los activos son divisibles: en nuestro caso, y a fin de poder comparar los resultados con el índice del mercado, en cada fecha sólo se considerarán como activos ofertados los que formen parte del índice.
- Existe un activo seguro: para nuestro estudio, como en otros trabajos citados, se tomará el rendimiento medio de la deuda pública con un vencimiento igual al período de inversión considerado.
- Los agentes económicos tienen expectativas homogéneas sobre las oportunidades de inversión.
- El mercado se considera competitivo.
- No se consideran costes de transacción, ni impuestos u otras fricciones.
- Los inversores escogen su cartera en función del rendimiento esperado y del riesgo, medido este último con la varianza, bajo la hipótesis de comportamiento gaussiano de los rendimientos de los activos y, además emplearemos una medida de Value at Risk (VaR) que considere otros momentos en el supuesto de no normalidad.
En este contexto, la estimación de la cartera de mercado se corresponde con la cartera tangente de activos inciertos, es decir, los agentes situarán sus decisiones de inversión sobre la denominada Capital Market Line (CML). Esta cartera óptima es la que más remunera por unidad de riesgo asumido, esto es:

La expresión (1) implica obtener una cartera de mercado (M), es decir, la combinación lineal de los activos que la conforman (wi), cuya rentabilidad esperada (E(RM)) sobre la tasa libre de riesgo (Rf) por unidad de riesgo (αM) es la mayor y, sujeto a una restricción presupuestaria básica sobre la inversión realizada en cada activo.
2.2. Metodología de estimación en entorno gaussiano
En la práctica este problema de optimización se encuadra dentro de un entorno gaussiano (hipótesis CAPM), por lo que la rentabilidad esperada se sustituye por la media muestral de los rendimientos de los activos (μ), el riesgo por su desviación estándar (σ) y la relación entre los rendimientos de los activos se considera lineal, por lo que se mide a través del coeficiente de correlación (ρ). Con todo ello, la expresión (1) se puede reescribir como:

Una forma habitual de resolver estos problemas de máximos consiste en derivar e igualar a cero, obteniéndose los pesos de los activos, de tal modo que si la segunda derivada es negativa la solución encontrada será un máximo (Marín y Rubio, 2001, pp. 260267), de tal modo que realizando un cambio de variable (z):

La expresión (2) puede escribirse en términos matriciales como:
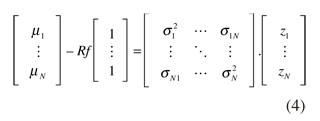
De tal modo que, podemos resolver fácilmente este sistema de ecuaciones y deshacer el cambio de variable como sigue:
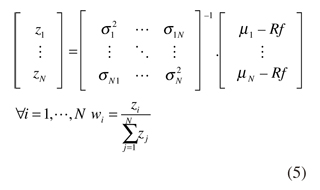
En la práctica, esta forma de resolución simple exige que podamos estimar la inversa de la matriz de covarianzas de los rendimientos de los activos, lo cual a su vez requiere que el determinante sea mayor que cero. Pero a medida que el número de activos aumenta se observa que el determinante converge a cero, consecuencia de la colinealidad1, por lo que no puede emplearse esta técnica. Por ello, en este trabajo se propone otra metodología de estimación: una optimización basada en un algoritmo genético (Simulating Annealing).
La ventaja de este procedimiento frente a otros métodos de optimización (v.gr. los quasi-Newton del tipo BFGS, BHHH) es que no requiere que la función sea diferenciable en todos los puntos, además realiza una búsqueda de valores más extensa sobre toda la superficie de valores factibles (conjunto de carteras potenciales).
Este procedimiento es sensible, como otros mencionados, al punto inicial de estimación, por lo que para evitar dicho inconveniente emplearemos la solución obtenida mediante el procedimiento iterativo Gauss-Seidel. Para encontrar los valores de las incógnitas dentro de una tolerancia deseada, en cada iteración (k), este método estima una nueva posible solución (Zik) a partir de los valores anteriores de cada incógnita (Zih ∀ h = 1, ..., k-1), y de los valores actuales del resto de incógnitas (Zjk ∀ j ≠ i). De este modo la solución iterativa puede expresarse como:

Una vez obtenidos los puntos iniciales, emplearemos el algoritmo Simulating Annealing sobre dos problemas de optimización bajo comportamiento gaussiano:
No se permiten las posiciones cortas; en este caso el problema de optimización se expresaría como sigue:

Se admiten posiciones cortas:

2.3. Metodología de estimación en entorno no gaussiano
Para el caso de comportamiento no gaussiano de las series de rendimientos, emplearemos la metodología propuesta por Jondeau y Rockinger (2006). Esta propuesta, para una función de utilidad CARA (Constant Absolute Risk Aversion), consiste en definir la condición de primer orden en función de momentos de mayor orden (media, varianza, asimetría y curtosis). De esta manera, si R es la matriz de rendimientos, es el μ vector de media, σ la matriz de covarianzas, s3 la matriz de co-asimetría y κ4 la matriz de co-curtosis:

Donde ® es el operador producto de Kronecker. Entonces dichos momentos para una cartera vendrán definidos por las siguientes expresiones:

Con lo que la condición de primer orden sería:

Siendo λ el coeficiente de aversión al riesgo.
De este modo, y para el supuesto de comportamiento no gaussiano, la función a optimizar sujeta a las mismas restricciones que en (7) y (8) sería:

Donde la varianza es sustituida por el Value at Risk (VaR ) como medida del riesgo. En concreto emplearemos un VaR paramétrico con la extensión Cornish-Fisher, tal que para un determinado nivel de confianza (α):

Donde Pt y Vt serán respectivamente el precio de los activos que componen la cartera y el valor de la cartera.
2.4. Metodología de contrastación de los resultados
Una vez obtenida la cartera tangente comprobaremos su eficiencia y la del índice del mercado de dos formas: en primer lugar emplearemos un test en sección cruzada para estimar a priori la eficiencia en cada instante temporal. Para lo que aplicaremos la propuesta de Shanken (1996), ello lo realizaremos del siguiente modo:
- En cada instante t estimaremos las β de los activos con respecto a la cartera tangente obtenida y el índice del mercado. Esta estimación se realizará con τ datos históricos.
- Seguidamente calcularemos la matriz de varianzas y covarianzas de los residuos (Σ) de las regresiones anteriores, y cuyo orden dependerá del número de activos del índice (N χ N).
- Como la estimación consistente del modelo es por GLS, es preciso determinar previamente la matriz de ponderaciones como: Ω = Σ + (β . β') . σ2. Donde σ2 es la varianza de los rendimientos de la cartera cuya eficiencia pretende contrastarse (tangente o índice). De este modo, podemos estimar el modelo sobre los rendimientos esperados o medios de los activos (μ): Γ = {β' Ω-1.β) \β' .Ω-1.μ . Donde el vector Γ tiene dos componentes, el rendimiento libre de riesgo (γ0) y la prima de riesgo del mercado (γ;). Estimado el modelo podemos determinar los errores: ε =μ - β.ρ
- Dado que las verdaderas β no son observables, introducimos la corrección de Shanken (1996) y definimos el siguiente estadístico:

Ahora bien, como este contraste sólo es aplicable bajo el supuesto de normalidad, en segundo lugar, contrastaremos si la estrategia de optimización propuesta sistemáticamente supera al índice de mercado, en una línea similar a Gómez-Bezares et al. (2012). Pero, mientras que Gómez-Bezares et al. (2012) proponen un z-test para los excesos de rendimientos de su estrategia de inversión frente al índice de mercado, en nuestro caso hemos de considerar adicionalmente la posible no-normalidad de las series y la condicionalidad en dichos excesos, empleando para ello un análisis del tipo backtesting.
En este sentido, contemplaremos las diferentes posibilidades que pueden darse, esto es, a priori, la cartera tangente obtenida puede tener mayor o menor performance que el índice del mercado, pero a pesar de ello, a posteriori, el rendimiento obtenido puede ser menor o mayor, con lo que para un total de T instantes temporales de contrastación (tamaño muestral) puede darse que:
1. La cartera tangente tiene a priori una performance mayor que la del índice (T¡ sucesos):
1.1. A posteriori la cartera tangente presenta un rendimiento menor o igual que el índice o error tipo-I (T¡ 1 sucesos).
1.2. El rendimiento a posteriori de la cartera tangente es mayor que la del índice o éxitos (T¡ 0 sucesos).
2. La cartera tangente tiene a priori una performance menor o igual que la del índice (T2 sucesos):
2.1. A posteriori la cartera tangente presenta un rendimiento menor o igual que el índice (T2 0 sucesos).
2.2. El rendimiento a posteriori de la cartera tangente es mayor que la del índice o error tipo-II (T211 sucesos).
De esta forma podemos estimar los siguientes contrastes de backtesting para un nivel de confianza α:
- Incondicional (Kupiec, 19952), esto es, los sucesos son independientes en el tiempo de modo que tendremos dos estadísticos el test Incondicional (1) y el de Kupiec (K):
- Condicional (Christoffersen, 1998), en este caso se asume un comportamiento dependiente markoviano de los sucesos, de este modo el test Condicional sería (L):
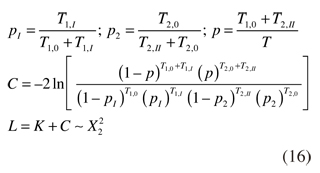
- Función de pérdida (López, 1999), que será una medida del error cometido y dependerá de los excesos de rendimiento a posteriori (exc), es decir, la diferencia entre los rendimientos posteriores entre la cartera tangente y el índice, en el primer caso, cuando a priori se seleccionó la cartera tangente y, en el segundo, cuando fue seleccionado el índice:

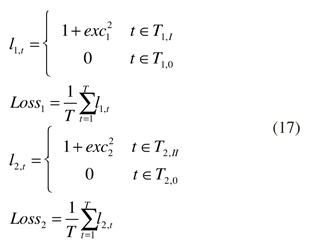
3. Datos
Para el estudio empírico se ha seleccionado como índice el IBEX-35, por lo que las empresas consideradas para construir posibles carteras tangentes que superen el índice como cartera de mercado sólo podrán estar construidas con los valores que en cada fecha compongan el índice de mercado.
Siguiendo con los trabajos citados que analizan el mercado español, empleamos los precios ajustados de dividendos y splits para el período que va desde enero-2000 hasta marzo-2013. Estos precios son obtenidos de Bloomberg. Lógicamente no todos los activos se han negociado durante todo este período temporal por lo que en el cuadro 1 mostramos las empresas consideradas, su ticker y el período muestral disponible.

El período de contrastación será menor que el tamaño total puesto que -como es habitual en la literatura- estimaremos los momentos muestrales en cada instante, siempre que existan suficientes datos, con los cinco años previos (60 datos mensuales), por lo que dicho período de contrastación irá desde enero-2005 hasta diciembre 2012. De manera que obtendremos 96 instantes temporales (uno al mes) de estimación de las carteras óptimas. Siguiendo la literatura, los rendimientos considerados serán en frecuencia mensual y trimestral, es decir, construida una cartera asumimos que se mantiene hasta el mes siguiente para los rendimientos mensuales, y hasta el siguiente trimestre en el caso de rendimientos trimestrales, tal y como se indicó las inversiones se consideran independientes (modelo CAPM estático). Adicionalmente, como realizamos un test a posteriori, para el caso de los rendimientos mensuales también se consideran los precios de enero-2013, mientras que para el caso trimestral se precisan desde enero hasta marzo de 2013.
En el Anexo en los cuadros 1A y 2A podemos observar un resumen estadístico de los rendimientos mensuales y trimestrales respectivamente. Por lo que respecta a los rendimientos mensuales.
Podemos observar como el índice se ajusta a las hipótesis de comportamiento de la teoría tradicional de carteras, en cambio hay títulos que no tienen un comportamiento gaussiano en el período de estudio, de manera que queda justificado el uso de momentos de orden superior para construir carteras óptimas.
En cuanto a los rendimientos trimestrales comprobamos que el número de títulos que presentan incumplimientos con respecto a las asunciones teóricas disminuye, lo que es consecuencia del Teorema Central del Límite (es decir, a medida que disminuye la frecuencia de observación muestral, los rendimientos tienden a comportarse como una normal ya que son suma de rendimientos no normales de frecuencia de observación mayor). Además los rendimientos son estimados over-lapping, evitando así problemas de autocorrelación y media móvil.
Finalmente, las tasas mensuales y trimestrales libres de riesgo son obtenidas del Banco de España (www.bde.es) y se corresponde con los rendimientos medios, en términos mensuales o trimestrales, de la deuda pública con vencimiento más próximo al mes y al trimestre respectivamente.
5. Resultados
En primer lugar, en el cuadro 2 pueden observarse los extremos (máximo y mínimo) y valor medio (mediana) de los diferentes momentos muestrales de las diferentes carteras óptimas estimados en cada uno de los 96 momentos considerados.
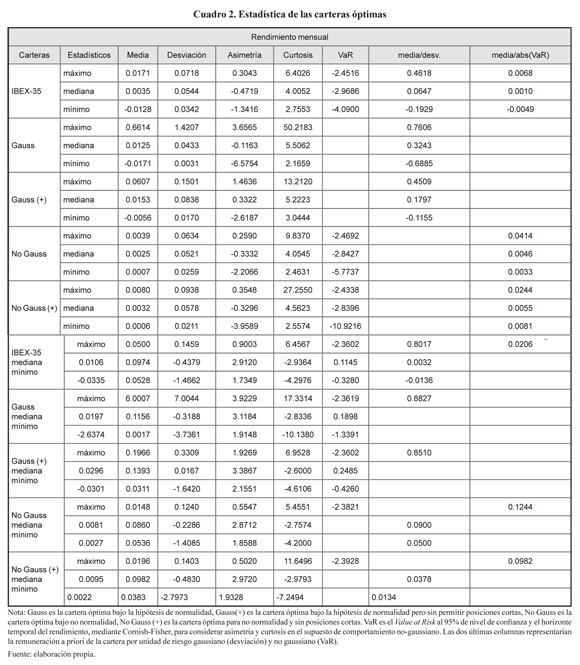
De los resultados obtenidos cabe destacar varios hechos relevantes:
- Al considerar que el comportamiento es gaussiano existen datos (véase el mínimo) con rendimiento esperado por unidad de riesgo negativo. Por el contrario, cuando se optimiza bajo la hipótesis de no-normalidad no sucede esto.
- Las carteras óptimas estimadas tanto bajo la hipótesis de normalidad como no, presentan a priori un rendimiento/riesgo mejor que el IBEX-35.
Seguidamente estimamos el test de Shanken para contrastar si las carteras son eficientes a priori. Como puede observarse en el cuadro 3 no podemos rechazar la hipótesis nula de ineficiencia, aunque también podemos comprobar que las carteras óptimas estimadas están más cerca de rechazar dicha hipótesis que el IBEX-35. Evidentemente no se ha estimado el test para las carteras no gaussianas puesto que la hipótesis del mismo es el comportamiento gaussiano de las series.

En el cuadro 4 se muestran las tablas de contingencia, tanto en términos mensuales como trimestrales:

Como puede observarse, en la mayoría de fechas cualquiera de las carteras óptimas resultaron a priori más eficientes que el IBEX-35, ahora bien, a posteriori sólo entorno al 50% de los casos presentaron una mayor rentabilidad. En resumen, a priori el IBEX-35 es superado por las carteras óptimas estimadas, pero al considerar los rendimientos a posteriori, dichas carteras no son la cartera de mercado en todos los casos, puesto que no se mantiene dicho exceso de rendimiento. Es destacable además, que las carteras óptimas en el supuesto de comportamiento no gaussiano muestran mejores resultados frente al IBEX-35, tanto ex ante como ex post, que bajo el supuesto de comportamiento gaussiano.
A partir de la tabla de contingencia podemos estimar los test de backtesting condicionales e incondicionales propuestos. En el cuadro 5 pueden observarse los resultados.

Como puede comprobarse únicamente en los casos de comportamiento no gaussiano, las carteras óptimas superan los test, tanto en frecuencia mensual como trimestral. Adicionalmente, presentan un menor nivel de excesos.
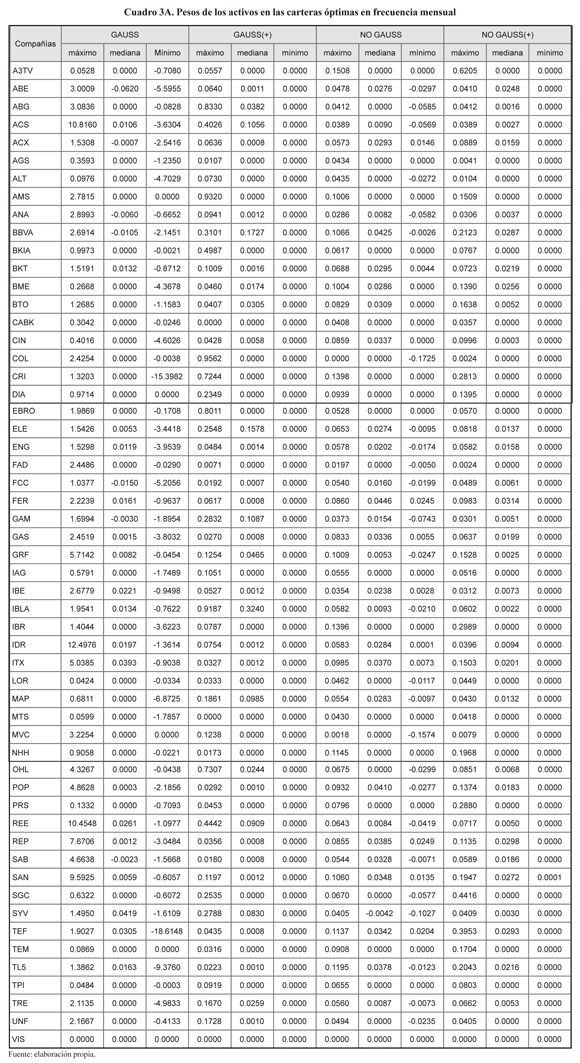
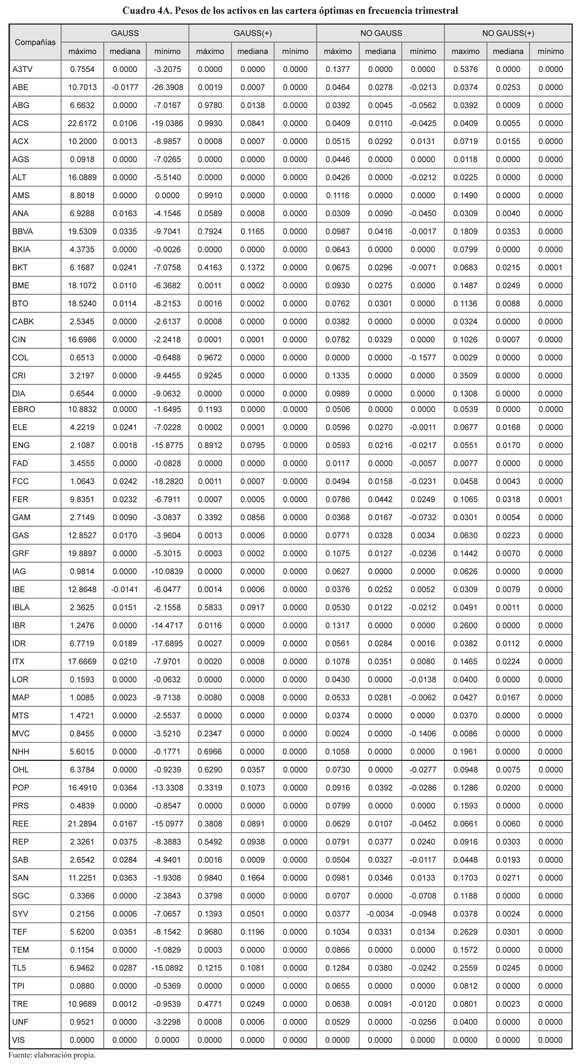
A continuación, en el cuadro 6 presentamos un resumen (la mediana de los pesos) de los resultados de la optimización tanto para la frecuencia mensual como trimestral. Una estadística de los pesos o ponderaciones de los diferentes activos en cada una de las carteras óptimas puede verse en el Anexo en los cuadros 3A y 4A.
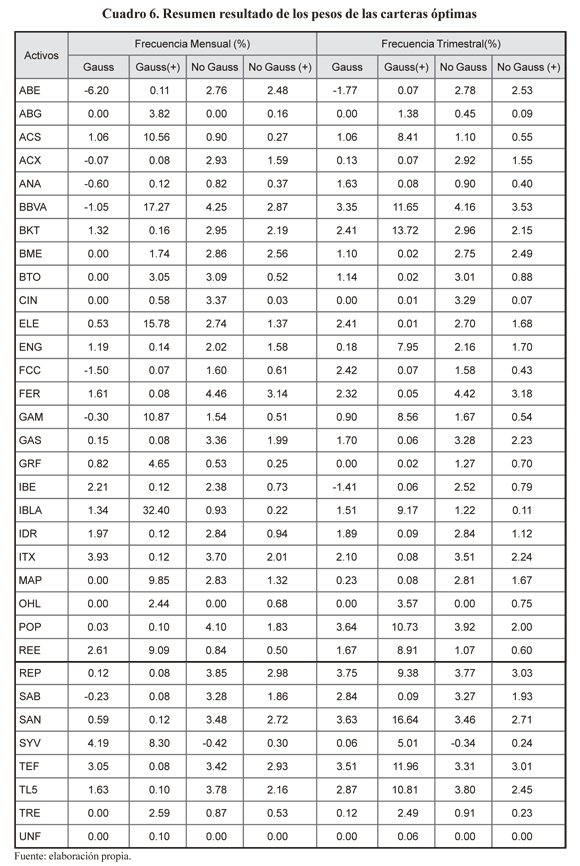
Se observa que en muchos casos los pesos de algunos activos en las carteras óptimas tienen como mediana valores nulos, esto es más frecuente en el caso de comportamiento gaussiano. Ello implicaría que no son necesarios 35 valores para obtener una cartera óptima a priori. Adicionalmente, esto queda refrendado por el hecho de que el promedio de los determinantes de las matrices de covarianzas es 7.96e-80 y 8.98e-62, para los rendimientos mensuales y trimestrales respectivamente, de manera que mostraría una alta colinealidad entre los rendimientos de los activos, con el consiguiente problema para la optimización por procedimientos estándares.
En el cuadro 7 mostramos la mediana de las betas de los activos que participan en las carteras óptimas con respecto dichas carteras y al IBEX-35. Un resumen estadístico de dichas betas puede verse en el Anexo en los cuadros 5A y 6A.
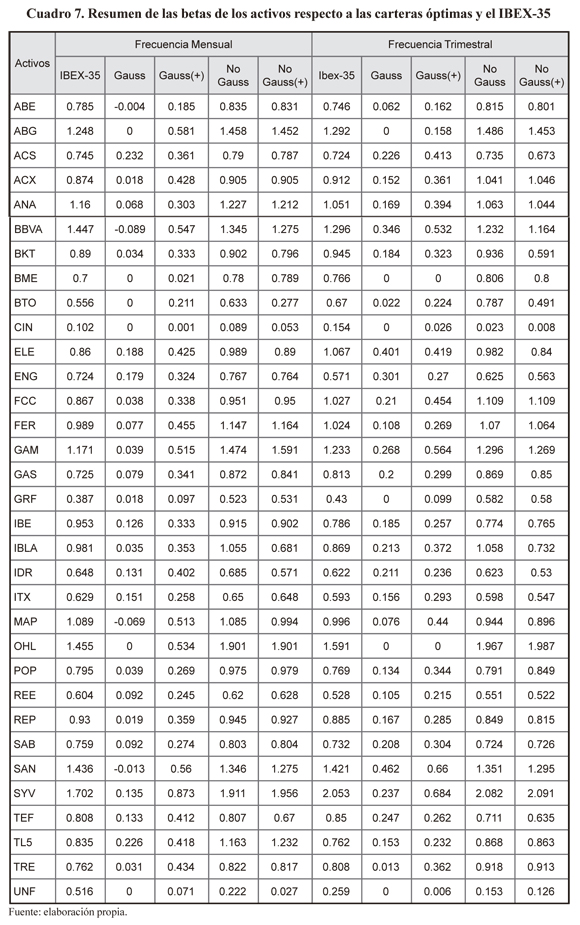
Y en función de dichas betas, en el cuadro 8, mostramos el rendimiento del activo libre de riesgo (γ0) y las primas de riesgo de mercado obtenidas.
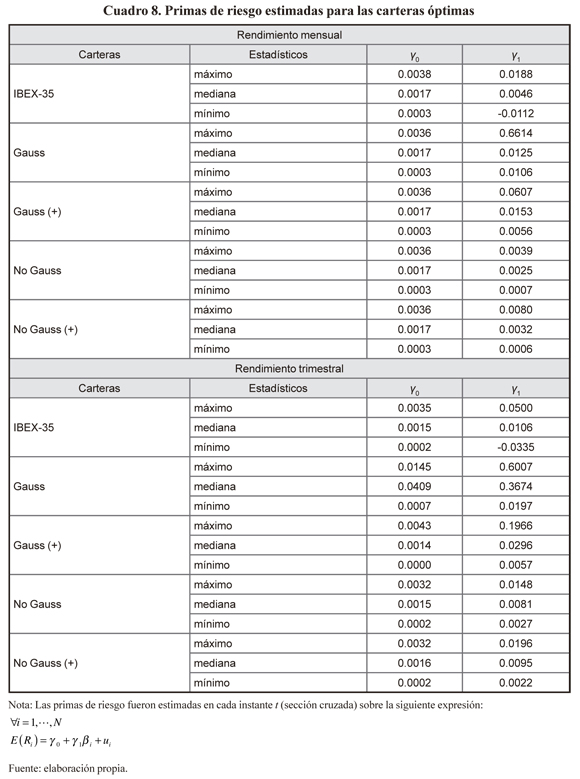
Un resultado relevante es que únicamente si empleamos como cartera de mercado el IBEX-35 obtenemos en algunos casos primas de riesgo de mercado (γ) negativas, lo que resulta incongruente. Adicionalmente, se observa que la restricción sobre las posiciones cortas para construir la cartera de mercado, conlleva mayores primas de riesgo con respecto a las carteras óptimas que admiten dichas posiciones.
4. Conclusiones
En la implementación de la Teoría de Valoración de Activos a través de la gestión de carteras es habitual emplear el índice de mercado como proxy de la cartera eficiente. Adicionalmente, la crítica de Roll (1977) indica que para considerar una combinación de activos como cartera de mercado es preciso que tanto a priori como a posteriori sea la que mayor rendimiento por unidad de riesgo ofrezca.
A raíz de esto, surgen trabajos en la literatura financiera que tiene por objeto comprobar si es posible "batir" el índice de mercado. Pero este objetivo no permite contrastar a priori al menos, si el índice del mercado es más eficiente en términos de rendimiento esperado por unidad de riesgo que otras carteras construidas con los mismos activos pero con otras ponderaciones.
Por ello, este trabajo pretende contrastar si es posible construir carteras más eficientes que el índice del mercado (IBEX-35) considerando exclusivamente los mismos activos que componen en cada momento el índice. Este análisis empírico se realiza bajo dos hipótesis de comportamiento de los rendimientos de los activos: gaussiano y no gaussiano.
Los datos analizados corresponden al período comprendido entre enero-2000 hasta marzo-2013, en términos mensuales y trimestrales. Se emplean, como suele ser habitual en los trabajos empíricos, cinco años de datos para la estimación de los momentos, de manera que el período de contestación va de enero-2005 hasta marzo-2013, con un total de 96 escenarios.
Un importante aporte del trabajo es que los resultados son analizados a través de pruebas de backtesting, de manera que no sólo se consideran los éxitos, sino también los errores de tipo-I y II. Otro aporte es el uso de un método de optimización diferente a los habituales (simulating annealing).
Los resultados obtenidos muestran los siguientes hechos relevantes para ambas frecuencias analizadas:
- En más del 90% de los casos las carteras obtenidas fueron a priori más eficientes que el IBEX-35.
- En torno al 50% de los casos las carteras que resultaron a priori más eficientes que el IBEX-35, también lo fueron a posteriori.
- En todos los casos las cartera óptimas estaban compuestas por un menor número de activos que el índice (menos de 35 valores); esta sobredimensión del índice se pone de manifiesto también mediante la colinealidad entre activos (el determinante de la matriz de covarianzas es nulo), y por tanto, conlleva problemas para la aplicación de técnicas estándar de optimización.
- En un entorno gaussiano ninguna de las carteras, incluyendo el índice, superó los test para considerarla como cartera de mercado.
- Las pruebas de backtesting son superadas únicamente por las carteras de entorno no gaussiano.
- Mientras que la prima de riesgo de mercado resultó positiva en todos los casos para las carteras óptimas, en el caso del IBEX-35 se observan valores negativos, lo que resulta incongruente con la teoría financiera. Además, la prima de riesgo fue mayor para las carteras que no admiten posiciones cortas.
En resumen, el IBEX-35 está sobredimensionado y es ineficiente, ya que podemos encontrar carteras bajo un entorno no gaussiano con mayor rendimiento esperado por unidad de riesgo. Como consecuencia, no resulta adecuado emplear este índice como cartera de mercado para el análisis y valoración de activos, por lo tanto la administración y gestión de carteras que considere activos en España debería:
- En primer lugar, evaluar si el comportamiento de los activos y de las carteras se ajusta a una distribución normal, ya que de lo contrario, el problema no puede plantearse en términos de media-varianza.
- Seguidamente, analizar qué activos deben ser incluidos para la estimación de la cartera de mercado. Resulta evidente que los 35 valores conllevan una sobredimensión del problema y un coste computacional y de recursos innecesario.
- Efectuar un seguimiento de la cartera óptima con metodologías como las propuestas aquí, que consideran los errores tipos I y II, de lo contrario podrían tomarse decisiones erróneas.
- Finalmente, señalar que a pesar de que el IBEX-35 es un índice de capitalización, la inclusión de la variable tamaño (volumen) no garantiza que un índice por construcción se aproxime a la cartera óptima de mercado.
Pie de página
1Aumentar el número de activos no significa necesariamente que el número de factores explicativos aumente, de tal modo que si se realiza una descomposición de la matriz de covarianzas en sus valores propios (Análisis de Componentes Principales) observaremos como al ir aumentando el número de activos, suele aparecer cada vez un número mayor de valores propios nulos, consecuencia de la colinealidad.
2Bajo la hipótesis de comportamiento normal de los sucesos, el test Kupiec equivale a un z-test.
Referencias
Arcos, M.; Benavides, J. and Berggrun, L. (2010). Optimal portfolio allocation for Latin American stock indices. Cuadernos de Administración, 23 (40), 191-214. [ Links ]
Brown, P. and Walter, T. (2013). The CAPM: Theoretical validity, empirical intractability and practical applications. Abacus, 49, 44-50. [ Links ]
Campbell, J. (2014). Empirical asset pricing: Eugene Fama, Lars Peter Hansen, and Robert Shriller. The Scandinavian Journal of Economics, 116 (3), 1-12. [ Links ]
Cantillo, A. (2013). Survey ofLiterature on Portfolio Theory. MPRA Paper 49772. Recuperado de: http://mpra.ub.uni-muenchen.de/49772 [ Links ]
Christoffersen, P. (1998). Evaluating interval forecasts. International Economic Review, 39, 841-862. [ Links ]
DeMiguel, V., Garlappi, L. and Uppal (2009). Optimal versus naive diversification: How inefficient is the 1/N portfolio strategy? The Review of Financial Studies, 22 (5), 1915-1953. [ Links ]
Ferruz, L. y Sarto, J. L. (1993). Medida de la eficacia de la gestión de los planes de pensiones en España, 1989-1991. Revista Española de Financiación y Contabilidad, 74, 105-131. [ Links ]
Gómez-Bezares, F.; Ferruz, L. and Vargas, M. (2012). Can we beat the market with beta? An intuitive test of the CAPM. Revista Española de Financiación y Contabilidad, 155, 333-352. [ Links ]
Gómez-Bezares, F.; Madariaga, J. A. y Santibáñez, J. (1996). Modelos de valoración y eficiencia: ¿bate el CAPM al mercado? Análisis Financiero, 68, 72-96. [ Links ]
Gómez-Sala, J. C. y Marhuenda, J. (1998). La anomalía del tamaño en el mercado de capitales español. Revista Española de Financiación y Contabilidad, 97, 1033-1059. [ Links ]
Jondeau, E. and Rockinger, M. (2006). Optimal portfolio allocation under higher moments. European Financial Management, 12 (1), 29-55. [ Links ]
Jordán, L. y García, J. (2002). Contraste del modelo CAPM en los fondos de inversión mobiliaria españoles. Revista Española de Financiación y Contabilidad, 114, 1041-1071. [ Links ]
Kupiec, P. (1995). Techniques for verifying the accuracy of risk management models. Journal of Derivatives, 3, 73-84. [ Links ]
Levy, M. and Roll, R. (2010). The market portfolio may be mean-variance efficient after all. The Review ofFinancialStudies, 23 (6), 2464-2491. [ Links ]
Lewellen, J., Nagel, S. and Shanken, J. (2010). A skeptical appraisal of asset pricing tests. Journal ofFinancial Economics, 96, 175-194. [ Links ]
Lopez, J. A. (1999). Regulatory evaluation of Value-at-Risk models. Journal of Risk, 1, 37-64. [ Links ]
Marín, J. M. y Rubio, G. (2001). Economía Financiera. Barcelona: Antoni Bosch. [ Links ]
Méndez, S. y Álvarez, S. (2000). La rentabilidad y persistencia de los resultados de los fondos de inversión españoles de renta variable. Revista Española de Financiación y Contabilidad, 103, 15-36. [ Links ]
Nieto, B. y Rubio, G. (2002). El modelo de valoración con cartera de mercado: una nueva especificación del coeficiente beta. Revista Española de Financiación y Contabilidad, 113, 697-723. [ Links ]
Roll, R. (1977). A critique of the asset pricing theory's tests. Part I: On past and potential testability of the theory. Journal ofFinancial Economics, 4, 129-176. [ Links ]
Rubio, G. (1986). La crítica de Roll y la solución de Shanken: una aplicación al caso español. Revista Española de Financiación y Contabilidad, 50, 379-393. [ Links ]
Shanken, J. (1996). Statistical methods in tests of portfolio efficiency: A synthesis. Handbook of Statistics, 14, Amsterdam: Elsevier Sciences. [ Links ]
Schlegel, A. (2014). Efficient Equity Indices A Literature Review. Institute of Financial Services Zug IFZ, Working Paper 0021/2014, Lucerne University of Applied Sciences and Arts. [ Links ]
Torre, O. de la (2013). No todo es lo que parece: El índice IBEX35 como aproximación de la cartera de mercado bursátil español. Análisis Financiero, 121, 64-76. [ Links ]
Villalba, D. (1998). Un modelo de selección de cartera con escenarios y función de riesgo asimétrica. Revista Española de Financiación y Contabilidad, 96, 613-637. [ Links ]