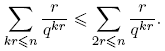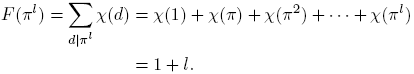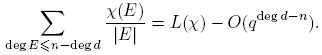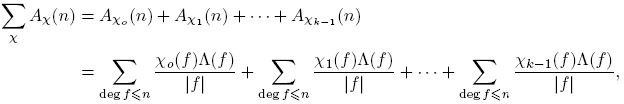1. Introducción
La progresión aritmética de números impares 1, 3, 5, . . . , 2k + 1, . . ., contiene infinitos números primos. Es natural preguntar si otras progresiones aritméticas tienen esta propiedad. Una progresión aritmética con el primer término a y diferencia común m consiste de todos los números de la forma
Si a y m tienen un factor común d, cada término de la progresión es divisible por d y no puede haber más de un primo en la progresión si d > 1. En otras palabras, una condición necesaria para la existencia de infinitos números primos en la progresión aritmética (1) es que (a,m) = 1. Johann P. G. L. Dirichlet fue el primero en probar que esta condición es también suficiente. Esto es, si m > 0 y a son enteros con (a,m) = 1, entonces hay un número infinito de primos p en la progresión aritmética (1), es decir, un número infinito de primos p con p ≡ a mód m. Este resultado es conocido como el teorema de Dirichlet.
De hecho, Dirichlet estableció que, en cierto sentido, los primos se distribuyen por igual en las progresiones. Euler probó la existencia de infinitos números primos mostrando que la serie Σ
pp
−1, extendida sobre todos los primos, diverge [4]. La idea de Dirichlet era probar una afirmación correspondiente cuando los primos están limitados a estar en la progresión dada (1). En una memoria famosa [3], publicada en 1837 realizó esta idea por ingeniosos métodos analíticos. En 1950, Harold N. Shapiro publicó una prueba elemental del teorema de Dirichlet [7]. Esta también la puede ver en [2]. La prueba de Shapiro realmente obtiene una estimación para  cuando (a,m) = 1, m > 0:
cuando (a,m) = 1, m > 0:
El análogo del teorema de Dirichlet en el caso de un anillo polinomial sobre F q fue, primero, probado en 1919 por Heinrich Kornblum [6, Capitulo 4]. La estructura de esta demostración es en gran parte la misma como en el caso clásico, y culmina con el análogo de la ecuación
Donde se puede ver que, en cierto sentido, los primos se distribuyen por igual en las progresiones.
Nuestro propósito es mostrar que la prueba de Shapiro y su estimación pueden ser adaptadas para el caso del anillo de polinomios Fq [t] (demostración basada a la mostrada por Paul Pollack en [5]). Es decir, probar que, dado un cuerpo finito Fq y polinomios a,m ∈ Fq [t] con (a,m) = 1, m ≠ 0, se tiene
El argumento de Shapiro puede ser considerado ligeramente más elemental, comparado con el de Kornblum, pues las series L que se necesitan son sumas finitas.
Para ello, se estudiaron las funciones aritméticas definidas sobre el monoide M(q; t). En particular, se usaron los análogos en M(q; t) de la función de von Mangoldt y de la función de Möbius conocidos en Z. Empleamos las propiedades de los caracteres de grupos abelianos finitos (caracteres de Dirichlet módulo m(t)) y sus relaciones de ortogonalidad en el estudio de la funciones L o L-funciones (llamadas series o funciones de Dirichlet ), L(s, χ), asociadas con un carácter χ módulo m(t). Se demuestra, usando un argumento bastante sencillo, uno de los pasos más difíciles de la prueba del teorema de Dirichlet: el poder establecer la no anulación de L(χ) para χ real no principal.
2. Preliminares
Fq denota a un cuerpo de característica p y cardinal q = pk , con p un número entero primo y k un número entero con k ≥ 1. P(q; T ) denota el conjunto de los primos de Fq [t], es decir, de los polinomios irreducibles unitarios. M(q; T ) denota el monoide de los polinomios unitarios con coeficientes en Fq .
Proposición 2.1. El conjunto U(Fq [t]/(m(t))), con m(t) ∈ Fq [t], definido por
es un grupo multiplicativo de orden φ(m(t)), donde φ es la función de Euler para los polinomios. En particular, si m(t) es un polinomio primo de grado k, entonces U(Fq [t]/(m(t))) = (Fq [t]/(m(t)))∗, los elementos no nulos de Fq [t]/(m(t)), es un grupo multiplicativo de orden φ(m(t)) = qk − 1.
Teorema 2.2 (Análogo del teorema de Euler). Si (a,m) = 1 con m(t) ∈ M(q; t), entonces
Véase la prueba en [1, Lección II, Sección 4] o en [6, Capítulo I].
Una consecuencia del teorema anterior es el siguiente:
Corolario 2.3 (Análogo del teorema pequeño de Fermat). Si p(t) ∈ P(q; t) tiene grado d y p(t) ∤ a(t), entonces
Definición 2.4. Una función con valor complejo definida en el monoide M(q; t) se llama una función aritmética. Una función aritmética f ≠ 0 es multiplicativa si f(mn) = f(m)f(n) siempre que (m, n) = 1, y es completamente multiplicativa si f(mn) = f(m)f(n) para todo par m, n ∈ M(q; t).
Definición 2.5. La función aritmética I dada por
se llama la función identidad.
Definición 2.6. El análogo de la función de Möbius μ está definida por
Teorema 2.7. [1, Lección VII, Proposición 6 (a)], [2, Capítulo 2, Sección 2] La función de Möbius satisface la relación
Teorema 2.8. La función de Möbius μ es multiplicativa.
Demostración. Sean a, b ∈ M(q; T ), y escribamos a = p
1
α1 · · · pr
αr
y b = q
1
β1 · · · qs
βs
tales que pi
, qj
∈ P(q;
T ). Si (a, b) = 1, entonces los pi
son distintos de los qj
. Si algunos de los αi
o de los βj
es mayor que 1, entonces a o b tiene algún divisor cuadrado que también lo será de ab. Por lo tanto, μ(ab) = 0 = μ(a)μ(b). Por el contrario, si α
1 = · · · = αr
= β
1 = · · · = βs
= 1, entonces μ(a) = (−1)
r
, μ(b) = (−1)
s
y μ(ab) = μ(p
1
α1 · · · pr
αr
q
1
β1 · · · qs
βs
) = (−1)
r+s
. Por lo tanto, μ(ab) = μ(a)μ(b). 
Definición 2.9. La norma | · | de un polinomio unitario de Fq [t] es una función | · | : M(q; t) → N tal que |a(t)| = qn con n = deg(a(t)). Como tal, esta función tiene las siguientes propiedades:
(I). |1| = 1,
(II). si p(t) ∈ P(q; t), entonces |p(t)| > 1, y
(III). |a 1(t)a 2(t)| = |a 1(t)||a 2(t)| para a 1(t), a 2(t) ∈ M(q; t).
Proposición 2.10 (Fórmula de la inversión de Möbius). Sean f y g dos funciones aritméticas. Suponga que para cada a ∈ M(q; t) la función
es multiplicativa. Entonces,
y la función f es multiplicativa.
Véase la prueba en [1, Lección VII, Proposición 9] o en [2, Capítulo 2, Sección 7].
Definición 2.11. El análogo de la función de von Mangoldt está definida por
Como Λ(1) = 0, esta función no es invertible y mucho menos multiplicativa.
Definición 2.12. Sea G un grupo abeliano finito, denotado multiplicativamente. Un homomorfismo f: G → C* se llama un carácter de G si f tiene la propiedad multiplicativa
para todo g 1, g 2 en G, y f(1 G ) = 1, donde 1 G es el elemento unidad de G. El conjunto de todos los caracteres de G se denota con Ĝ, esto es
Todo grupo admite, por lo menos, un carácter fo (g) := 1, para todo g ∈ G. A este carácter se le llama principal. Si f 1, f 2 ∈ Ĝ, podemos definir una ley de composición interna sobre Ĝ, de la siguiente manera:
para cualquier g de G. Además, fof = ffo = f, para cualquier f ∈ Ĝ.
Definición 2.13. Sea m ∈ Fq [t] un polinomio no constante fijo. Sea χ′ : (Fq [t]/(m(t)))* → C* un homomorfismo. Dado χ′, definamos χ: F q [t] → C* de la siguiente forma:
Las funciones χ definidas de esta manera son llamadas caracteres de Dirichlet módulo m. El carácter principal χo es el que tiene las propiedades:
Definición 2.14. Sea m ∈ Fq[t]. Una función χ: Fq [t] → C* se llama un carácter multiplicativo módulo m si para cada a, b ∈ Fq [t] se tiene:
(I). χ(a) = 0, si (a,m) ≠ 1.
(II). χ(1) ≠ 0.
(III). χ(ab) = χ(a)χ(b).
(IV). a ≡ b mód m, entonces χ(a) = χ(b).
Los caracteres de Dirichlet (que están definidos en Fq [t]) inducen y están inducidos por elementos en el grupo de caracteres de (Fq [t]/(m(t)))*. Por consiguiente, hay exactamente φ(m) caracteres de Dirichlet módulo m(t). Los caracteres módulo m(t) de un grupo abeliano finito satisfacen ciertas relaciones de ortogonalidad. Aquí tomamos G = (Fq [t]/(m(t)))*. Para nosotros, estas relaciones toman las siguientes formas:
Lema 2.15. [1, Lección VII, Proposición 13] o en [2, Teorema 6.16]. Sean χ 1, · · · , χo (Ĝ) caracteres de Dirichlet módulo m (asumiendo χ 1 como el carácter principal) y u, v ∈ F q [t] con (v,m) = 1. Entonces,
donde
3. Teorema de Dirichlet en F q [t], forma fuerte
Antes de proceder, introducimos un poco de notación: para p ∈ Fq [t] se define φ(p) como el cardinal del grupo de unidades de Fq [t]/(p). De aquí en adelante, π siempre denota un mónico irreducible de Fq [t], d, f siempre denotan polinomios mónicos, n siempre denota un entero no negativo. Las sumas de polinomios siempre se entiende que deben tomarse solo sobre polinomios mónicos. Con estos acuerdos, el principal resultado de este trabajo se puede expresar de la siguiente manera:
Teorema 3.1. Sean F q un cuerpo finito, a,m ∈ F q [t] con (a,m) = 1 y m ≠ 0. Entonces, para n ≥ 0,
En primer lugar demostraremos un análogo de la estimación log[x]! = x log x − x + O(log x).
Lema 3.2. Para n ≥ 0,
Demostración. Sea S: = Σdeg(f)≤n log |f|. Puesto que |f| = q deg(f), entonces
tomando k = deg(f). Puesto que Σdeg(f)=k 1 = qk para f(t) ∈ Fq [t], entonces
por lo tanto,
pues Σ n k =1 qk es una progresión geométrica. Entonces,
También necesitaremos algunos resultados elementales sobre la distribución de primos en F q [t]. Estos serán consecuencias sencillas de los siguientes:
Teorema 3.3 (Teorema del número primo para Fq [t]). Sea Fq un cuerpo finito. Sea vq (n) el número de polinomios primos (mónicos) de grado n en Fq [t]. Para n ≥ 1, Σ d|n dvq (d) = qn . Así,
Demostración. Consideremos la factorización prima de tqⁿ − t en Fq [t] y sea π(t) un primo mónico de grado d. Si d|n, entonces
por el análogo del teorema pequeño de Fermat. Por consiguiente,
Recíprocamente, si π(t)|(tqⁿ
− t), escogemos  como un generador del grupo multiplicativo (F
q
[t]/(π(t)))*. Entonces, dado que, tqⁿ
≡ t mód π(t), tenemos tqⁿ
= t+h(t)π(t) con h(t) ∈ F
q
[t]. Si g(t) = g
0 + g
1
t + · · · + gktk
, donde cada gi
∈ F
q
, tenemos g(tqⁿ
) ≡ g(t) mód π(t). Por otro lado,
como un generador del grupo multiplicativo (F
q
[t]/(π(t)))*. Entonces, dado que, tqⁿ
≡ t mód π(t), tenemos tqⁿ
= t+h(t)π(t) con h(t) ∈ F
q
[t]. Si g(t) = g
0 + g
1
t + · · · + gktk
, donde cada gi
∈ F
q
, tenemos g(tqⁿ
) ≡ g(t) mód π(t). Por otro lado,
y, además,
puesto que F q es un dominio de integridad con q − 1 unidades y de característica p. Entonces,
es decir,  . Como
. Como  ∈ (F
q
[t]/(π(t)))*, existe
∈ (F
q
[t]/(π(t)))*, existe  ∈ (F
q
[t]/(π(t)))* tal que
∈ (F
q
[t]/(π(t)))* tal que  . Además, puesto que o((
. Además, puesto que o(( )) = qd
− 1, entonces qd
− 1|qn
− 1, lo que obliga a que d|n. Sea
)) = qd
− 1, entonces qd
− 1|qn
− 1, lo que obliga a que d|n. Sea
la factorización única de tqⁿ − t en polinomios mónicos irreducibles. Por lo que se probó anteriormente, cada irreducible mónico de grado divisor de n debe ser o aparece como uno de los πi , y cada πi es un irreducible mónico de grado divisor de n (pues, πi | tqⁿ −t). Además, ningún πi aparece más de una vez. De esto, se deduce que
Como
entonces, comparando grados, se tiene
La fórmula para νq (n) se sigue de la fórmula de la inversión de Möbius (Proposición 2.10), así: tomando g(n) = qn y f(d) = dνq (d), se tiene
entonces
Por otro lado, veamos que
Si n = 1, entonces d = 1. Por lo tanto,
Pero, q = q + 0 = q + O(q 1/2 + q 1/3). Por consiguiente,
Si n = 2, entonces d = 1 o d = 2. Por lo tanto,
Pero, | − q| = q < q 2/2 + 2q 2/3. Es decir, −q = O(q 2/2 + 2q 2/3). Entonces,
Si n es un número primo > 2, entonces d = 1 o d = n. Por lo tanto,
Como n > 2, entonces qn /2 > q, pues n/2 > 1. Entonces, |−q| = q < qn /2 < qn /2+nqn /3. Es decir, −q = O(qn /2 + nqn /3). Luego, (6) se verifica para un primo n > 2. Suponga que n es un número con las siguientes formas: Si n = 2t, con t = 2, 3, · · · , entonces,
donde
Por otro lado, como  , entonces qd
< qn
/3 y, además, |μ(n/d)| ≤ 1; por consiguiente,
, entonces qd
< qn
/3 y, además, |μ(n/d)| ≤ 1; por consiguiente,
donde t 1, t 2, · · · , tr son los divisores de n menores que n/4. Por lo tanto,
Entonces,
Si n = 3t, con t = 2, 3, · · · , entonces,
donde
Por otro lado,
donde t 1, t 2, · · · , tr son los divisores de n menores que n/3. Así, de esta forma, se verifica (6). Análogamente, (6) se verifica si n = pt, donde p es un entero primo y t ∈ Z+. De acuerdo con lo anterior, (6) se cumple para n ≥ 1.
De (6) se tiene
Lema 3.4. Para cada f,
También,
Demostración. Sea f = π1 a1 π2 a2 · · · πkak con πi primo, para 1 ≤ i ≤ k. Entonces,
Por lo tanto,
Por otro lado, si d ∈ {π 1, π 2 1, · · · , π 1 a1 , π 2, π 2 2, · · · , π 2 a2 , · · · , πk , π 2 k , · · · , πk ak }, entonces Λ(d) ≠ 0, por lo cual
debido a (7). La segunda afirmación se sigue por una generalización apropiada de la fórmula de la inversión de Möbius. Podemos dar una prueba directa de la siguiente manera:
Para evaluar el lado izquierdo es suficiente restringir la suma a divisores libres de cuadrados d. Expandiendo log |d| formalmente, tenemos
donde π son los divisores primos de f distintos mutuamente, y k es el número de divisores primos de f distintos mutuamente. De esta manera,
Nótese que para k = 0, de modo que f = 1, la suma de la derecha es vacía. Si k = 1, entonces f = π
1
a1 , y el lado derecho se evalúa como −log |π
1|. Si k ≥ 2, la suma interior es igual a −(1−1)
k−1 = 0. Por lo tanto, en cualquier caso el resultado se demuestra. 
Del Teorema 3.3 podemos inferir lo siguiente:
Afirmación 3.5. La suma de los grados de todos los polinomios primos π(t) en F q [t] que dividen al entero positivo r es qr . Esto es,
Lema 3.6. Para n ≥ 0,
Observación 3.7. Esta es otra forma del teorema del número primo para Fq[t]. Aquí tenemos una fórmula exacta y simple para esta suma.
Demostración.
pues deg πk = k deg π. Si r = k deg π con k ≥ 1, entonces 1 ≤ deg π ≤ r ≤ n. Por lo tanto, por la Afirmación 3.5, tenemos
Por otro lado, como log q < q − 1, entonces
Es decir,
Considerando los resultados anteriores, se sigue la igualdad deseada. 
Lema 3.8. Para n ≥ 0,
También,
Demostración. La primera igualdad se sigue por la reordenación de la suma, al igual que cuando se prueba la afirmación análoga sobre Z. De esta forma tenemos
Entonces,
Por otro lado, si r = deg π, tenemos
Por consiguiente,
Por otro lado, nótese que para k ≥ 2, se tiene
Entonces, multiplicando ambos lados de la desigualdad anterior por log q, se tiene
Lo anterior implica que
Luego, de (8), tenemos
También, 2qk ≤ q 2k para k ≥ 1. Por consiguiente,
Si k = deg π, tenemos
Como consecuencia,
Entonces,
pues, existe M > 0 tal que . De aquí resulta
. De aquí resulta
Finalmente, puesto que
obtenemos,
De esta manera, se tiene
De la prueba del Lema 3.6, ψ(k) − ψ(k − 1) = qk log q, cuando k ≥ 1; por tanto,
Refiriéndonos a la primera parte del lema, tenemos
Definición 3.9. Sea s = σ + iγ un número complejo. Para un carácter no principal χ módulo m(t), con m(t) ∈ F q [t], definamos
como la función L asociada a χ.
Definición 3.10. Para un carácter no principal χ módulo m(t), con m(t) ∈ F q [t], hagamos
Aparentemente, la suma anterior es infinita. Sin embargo, más adelante vamos a demostrar que cuando k ≥ deg m, ck = 0, de manera que en la definición de L(χ) solo se necesita la suma hasta k = deg m− 1.
Proposición 3.11. Para cualquier carácter χ módulo m sobre F q [t], la serie
es absolutamente convergente para σ = Re(s) > 1.
Demostración. Tomemos σ = R(s) > 1. Como |f| = qk , donde k = deg f, y existen qk polinomios mónicos de grado k, tenemos, para todo k = 0, 1, 2, . . ., lo siguiente:
Luego,
Por lo tanto,
Ahora podemos establecer la no anulación de L(χ) para χ real no principal. Considerando que la próxima afirmación es uno de los pasos más difíciles de la prueba del teorema de Dirichlet sobre Z, aquí se trabaja un argumento bastante sencillo.
Teorema 3.12. Si χ ≠ χo es un carácter de Dirichlet real módulo m, entonces L(χ) ≠ 0.
Demostración. Definamos  , la cual es una función multiplicativa, pues χ es una función multiplicativa. Ahora, como χ es real, tenemos: si χ(π) = 0, entonces F(πl
) = χ(1) = 1; si χ(π) = 1, entonces
, la cual es una función multiplicativa, pues χ es una función multiplicativa. Ahora, como χ es real, tenemos: si χ(π) = 0, entonces F(πl
) = χ(1) = 1; si χ(π) = 1, entonces
Finalmente, sea χ(π) = −1. Como
concluimos que
Por lo tanto, siempre se tiene F(πl
) ≥ 0, con F(πl
) ≥ 1 si l es par. Consecuentemente, siempre se tiene F(f) ≥ 0, y en particular, F(f) ≥ 1 si f es un cuadrado (es decir, f es de la forma π2i, con i = 0, 1, · · · ). Para un número natural z, definamos  .
.
Entonces,
De donde tenemos que
Por otro lado,
Por consiguiente,
Luego para z ≥ deg m− 1,
donde  es constante. De esta manera, si L(χ) = 0, S(z) = c para z ≥ deg m−1, contradiciendo lo probado en (12). Esta contradicción completa la prueba.
es constante. De esta manera, si L(χ) = 0, S(z) = c para z ≥ deg m−1, contradiciendo lo probado en (12). Esta contradicción completa la prueba. 
Ahora, estamos listos para movernos a la parte principal del argumento: Estudiaremos las funciones  .
.
Teorema 3.13. Para n ≥ 0, Aχo (n) = log(qn ) + O(1).
Demostración. Nótese que, si (gk ,m) = 1, para k ≥ 1, con g y m en M(q; T ), entonces (g,m) = 1. De lo anterior se tiene
donde
Por otro lado, como
para k ≥ 2, entonces
con la ayuda de la prueba del Lema 3.8. Por lo tanto,
por las propiedades de O-grande, y por el Lema 3.8. 
El resto de esta sección está dedicada a mostrar que para χ ≠ χo , Aχ (n) = O(1). El Teorema 3.1 se seguirá de este resultado, del Teorema 3.13 y las relaciones de ortogonalidad.
Lema 3.14. Sea χ un carácter no principal. Para n ≥ 0,
Demostración. Como se demostró anteriormente, la función de la izquierda se anula para k ≥ deg m. También se anula para n ≥ deg m − 1. Por otro lado, supóngase que n ≤ deg m − 2. Nótese que
Entonces,
Lema 3.15. Sea χ un carácter no principal. Para n ≥ 0,
Demostración. Por el Lema 3.4,
Además,
puesto que, para f = Ed,
Ahora, por el Lema 3.14,
Por lo tanto,
Entonces,
para M > 0. O sea, R(n) = O(q −n Σdeg d≤n Λ(d)) = O(q − nqn ) = O(1), por Lema 3.6. Puesto que para n ≥ deg m, ck = 0, se sigue que
donde c es una constante. Entonces,
Luego,
De lo anterior deducimos inmediatamente el
Corolario 3.16. Si L(χ) ≠ 0 para el carácter no principal χ, entonces Aχ (n) = O(1).
Lema 3.17. Sea χ un carácter no principal. Para n ≥ 0,
En particular, si L(χ) = 0, Aχ (n) = −log(qn ) + O(1).
Demostración. Evaluemos  de dos maneras diferentes. Nótese que, por Lema 3.4
de dos maneras diferentes. Nótese que, por Lema 3.4
Por Teorema 2.7, se tiene
Luego, por un lado,
pues, f = 1 cuando deg f = 0, y f ≠ 1 cuando 0 < deg f. Por otro lado, invirtiendo el orden de la suma, tenemos
donde f = hd (prueba análoga a (13)). Además, por Lema 3.14,
Luego la expresión que está a la derecha se convierte en
para M > 0. Después, expandiendo la progresión geométrica y restando la expresión obtenida en el Lema 3.2, vemos que
Entonces, R(n) = O(1), pues |R(n)| ≪ q − nqn = 1. Comparando las dos expresiones obtenidas, tenemos
Juntando este resultado con el del Corolario 3.16, vemos que hemos demostrado el
Lema 3.18. Sea χ un carácter no principal. Entonces, para n ≥ 0
Demostración. Del Lema 3.17 tenemos, para n ≥ 0,
Si L(χ) = 0, entonces Aχ (n) = O(1) + log(qn )(−1). Por otro lado, del Corolario 3.16 tenemos, si L(χ ≠ 0,
De esta forma concluimos la afirmación del lema. 
Corolario 3.19 (No anulación de L(χ) para χ no real). Si χ es un carácter que toma al menos un valor no real, L(χ) ≠ 0.
Demostración. Por Lema 2.15, si f ≡ 1 mód m, entonces Σ χ χ(f) = φ(m). Además,
pues G Ĝ, tomando o(G) = k. Entonces,
Ĝ, tomando o(G) = k. Entonces,
Es decir,
Por otro lado, del Teorema 3.13 y del Lema 3.18 tenemos
donde V es el número de caracteres χ tales que L(χ) = 0, es decir, 1 ≤ V ≤ k−1. Nótese que log |π| = deg π log q > 0, pues log q ≥ log 2 y deg π ≥ 1. Entonces,
Puesto que el lado izquierdo de (14) es no negativo para todo n, debemos tener V ≤ 1. Pero si L(χ
1) = 0 para un carácter no real χ
1, entonces  . Dado que χ1 toma, al menos, un valor no real, χ
1 ≠ χ̅1 y, por tanto, V ≥ 2, hay al menos dos caracteres χ diferentes tales que L(χ) = 0, contradiciendo lo anterior.
. Dado que χ1 toma, al menos, un valor no real, χ
1 ≠ χ̅1 y, por tanto, V ≥ 2, hay al menos dos caracteres χ diferentes tales que L(χ) = 0, contradiciendo lo anterior. 
Puesto que por el Corolario 3.19 y el Teorema 3.12, L(χ) ≠ 0 para cada χ no principal, el Corolario 3.16 implica el esperado
Corolario 3.20. Si χ es un carácter no principal, Aχ (n) = O(1).
Demostración del Teorema 3.1. Por Lema 2.15, Teorema 3.13, y Corolario 3.20, tenemos:
Como G Ĝ, tomando o(G) = k, se tiene
Ĝ, tomando o(G) = k, se tiene
Por otro lado,
pues (a,m) = 1. Por lo tanto,
Ahora,
donde
Como
entonces
Por consiguiente,
Por tanto, como m ≠ 0,