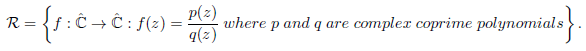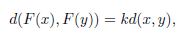English (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
1. Introduction
In this paper we will deal with the class of automorphisms on the Riemann sphere, denoted by R, where
P. Fatou and G. Julia in 2 and 4 studied the iteration of functions with degree at least two in the class R, that is, the convergence on compacts of sequence of iterates of the function f, {f n } n∈ ℕ, where f n is the composition of f with itself n times. In particular, when n = 0 and n = 1, f 0 = Id and f 1 = f, respectively. Observe that the class of rational functions R is a semigroup with the composition of functions, i.e., if f ∈ R, then f n ∈ R. They consider the iteration of all the points z ∈ Ĉ under f ∈ R and obtain two disjoint sets, namely, the Fatou set, denoted by F(f), which is the set of point z ∈ Ĉ such that the sequence of iterates of f forms a normal family in a neighbourhood of z and the Julia set, which is the complement of the Fatou set and denoted by J(f) = Ĉ \ F(f).
We recall some well known properties of the Fatou and Julia sets for rational functions: (i) F(f) is open, so J(f) is closed; (ii) J(f) is perfect and non-empty; (iii) the sets J(f) and F(f) are completely invariant under f; and finally (iv) the repelling periodic points are dense in J(f) (see 1 for a proof).
D. Sullivan in 8 classifies the connected components U of the Fatou set of a rational function f as follows: (i) attracting, (ii) parabolic and (iii) linearizable rotation domains (Siegel disk and Herman ring).
In this paper we are particularly interested in Herman rings, whose existence was proved by Herman in 3, and later on Shishikura in 5 constructed them using quasiconformal surgery. A significant characteristic of these kind of components is that their existence is not related to the existence of periodic points like the others (see 1 for a proof).
In 6 Shishikura studies the realization problem, which is an inverse construction to the existence theorem; that is, he studied the conditions under which there exists a rational f such that given a finite collection with p elements of topological annuli that will correspond later on to a p-cycle of Herman rings for some function f. In order to do that, he constructed three objects: a topological tree T associated to the collection of topological annuli, a linear metric d on Cˆ and a continuous function F onto T, which conform a Shishikura’s triple.
In what follows, we shall explain the construction of the elements that conform a Shishikura’s triple, say (T,d,F), and we give the procedure for obtain the orbit model on (T,d,F). Finally, we enunciate the Realization theorem for rational functions.
Organization of the paper. This paper contains two sections. In Section 2 we explain the necessary elements to guarantee the realization of a configuration of a p-cycle of Herman rings for a rational function through a construction of a Shishikura’s triple given in 6 and 7, and Section 3 contains examples of some realizable configurations and the procedure to obtain them.
2. Shishikura’s triple and the Realization theorem
We recall that a component U in the Fatou set is called:
A p-cyclic Siegel disc if there exits an analytic homeomorphism φ: U → D, where D is the unit disc, such that φ conjugates f p with e 2πα z for some α ∈ ℝ \ ℚ, where α is called the rotation number of the disc.
A p-cyclic Herman ring if f p is conformally conjugate to an irrational rotation on a concentric annulus, that is, there exist 0 < r 0 < 1, θ ∈ (0,1)\ ℚ and a conformal change of variables h H : H r0,1 → H such that f p ◦ h = h ◦ R θ , where R θ is the rigid rotation of angle 2πθ, and H r0,1 is the standard annulus of inner radius r 0 and outer radius 1.
A configuration for a p-cycle of Herman rings is defined as follows: fix r such that r 0 < r < 1 and define γ 0 = h − H 1({z ∈ ℂ :| z |= r}) with a determined orientation and γ j = f j (γ 0); then f induces equivariant orientations of γ j , and {γ j } defines a configuration, which is independent of the choice of r and the orientation of γ 0 .
Shishikura in 6 studies the conditions under which a finite arrangement of topological annulli D := {A 0 ,...,A p1 } corresponds to a configuration of cyclic Herman rings (the elements in D satisfies that for some i,j, A i ⊂ A j or, for every i,j, A i ∩ A j = ∅ or the combination of the two cases). In order to do that, on D constructs three objects: a topological tree T, a linear metric d on Cˆ and a continuous function F onto T, which conform a Shishikura’s triple.
In the same paper, he defines an orbit model on (T,d,F) in order to obtain f ∈ R and a collection of Herman rings {H 0 ,H 1 ,...,H p1 } such that {H 0 ,H 1 ,...,H p1 } is a p-periodic cycle of Herman rings of f, with f(H i ) = H j for some i,j ∈ {0,...,p1}. When these conditions are satisfied, it is said that f realizes the configuration D.
It should be mentioned that initially we obtain a rational function with a p-cycle of Siegel discs, which via quasi-conformal surgery is transformed into Herman rings (see [5] for a proof).
2.1. Abstract tree
Consider D as in Section 2 and assume that there exists a non-empty closed set B such that B consists of a finite number of connected components B 1 ,...,B n , where none of them is a point and each A ∈ D is disjoint with B and separates B.
In this part, we will construct an abstract tree associated to the configuration D. For that, consider on Ĉ an equivalence relation ∼ d as follows: for x,y ∈ Ĉ, x ∼ d y if, and only if, d(x,y) = 0, where d is a metric given by d(x,y) = ∑ A∈D mod(A(x,y)), which is continuous on Ĉ × Ĉ and d is a pseudo-metric on Ĉ. Thus, the quotient space
is called the abstract tree associated to the configuration D.
Furthermore, T(D) is indeed a topological finite tree, this is, a one-dimensional finite simplicial complex which is connected and without loops. Moreover, T(D) is the union of specific arcs with determined end points and satisfies that the projections π(A) are dense in T(D) and are isometric to open intervals. For a proof see 6.
A. Algorithm for obtaining the tree associated to a configuration D.
Intuitively it is possible to construct T as it shall follow the following algorithm, which is exemplified in each step.
Consider a collection C of topological annuli with the conditions mentioned in Section 2.1 (see Figure 1(a)).
Now, in C consider a graph Γ whose vertices are the connected components of the complement of the annuli (see Figure 1(b)).
Two vertices are connected by an edge if, and only if, the corresponding two verticeshave a common annulus whose boundary is contained in them (see Figure 1(c)).
Thus, we obtain a tree as follows.
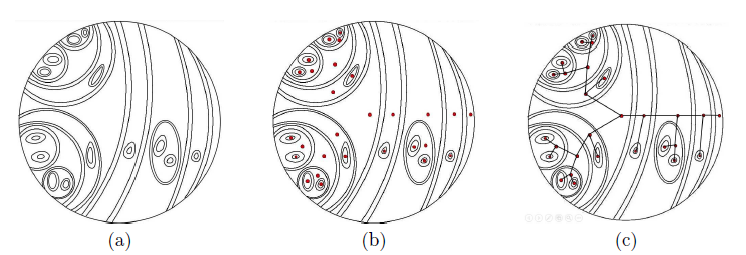
Figure 1 (a) Configuration C of topological annuli. (b) Vertices of the tree associated to the configuration C. (c) Edges for a configuration C.
2.2. Shishikura’s tree associated to a configuration given by a p-cycle of Herman rings
With base to the previous definition of an abstract tree we are able to define a Shishikura’s tree for a configuration of a cycle of Herman rings (see 6, 7). Let f ∈ R and f n the n-iterate of f. Take f such that it has a p-cycle of Herman rings {H 0 ,...,H p1 }, and define the following sets:
C = {f n (z)|z is critical point of f, n ≥ 0};
A 0 = {connected components of H 0 \ closure(H 0 ∩ C)};
A ′ = {connected components of f −n (A) : A ∈ A0 , n ≥ 0};
B = ∪∂H i , where ∂H i denotes the boundaries of the Herman ring H i , and
A = {A ∈ A ′ : A is essential}, where an annulus A ∈ A ′ is essential, if f n (A) separates B for all n ≥ 0.
The sets A 0 , A ′ and A are collections of disjoint annuli. Taking A as D and B as B in the previous section, T(A) is a metric space and d can be projected to a linear metric. T(A) is called a Shishikura’s tree which is denoted by T.
2.3. Continuous function on T
Let T be as Shishikura’s tree and F: T → T be defined by
where π is the canonical projection and ∂(π −1(x)) is the boundary of π −1(x) in Ĉ; this function is well-defined and continuous.
It is observable that f induces a map on T and therefore a permutation on the elements of T. Moreover, it satisfies that if J ⊂ T is an arc that does not contain any branch points or the image under π of a critical point of f, then R = π −1(J) is an annulus and f : R → f(R) is a convering map degree of degree k for some k ∈ ℕ and
so that DF(z) := k denotes an unbranched point z ∈ (x,y).
It follows from the construction of T that F is a piece wise linear function that acts as a permutation on the elements of T, and the arcs I j can be oriented in such way that f respects the orientations, that is, considering ∂ − I j and ∂ + I j the beginning and the end of the arc I j , then ∂I j = {∂ − I j ,∂ + I j } and F(∂ − I j ) = ∂ − I j+1 , F(∂ + I j ) = ∂ + I j+1 .
Thus, in order to represent T we need a finite set of arrowed segments, denoted by x 1 ,...,x n , and their respective lengths as well as a periodic arc, x n+1 , with its end points.
2.4. Local models
Now, we will explain how Shishikura in 7 gets a rational function f that realizes a configuration of Herman rings, for which the concept of local model for singular orbits is needed. Since each complementary component of A is collapsed to a point, we lose the dynamics, which can be recovered by defining local models via surgery. The plan behind this concept is as follows.
First, consider a tree associate to a configuration of annulli (see Figure 3).
Second, thicken all the segments of the tree to tubes with a small common radius, blowing up all the singular points to balls. Gluing the balls and the tubes, a topological sphere is obtained (see Figure 4).
Finally, define a function on the tubes so that if x,F(x) 6∈ Sing(T,F), it is a covering of degree DF(x) from the circle corresponding to x to that corresponding to F(x). Thus, we define a rational function with the same degree as the the local degree of F. We obtain a cyclic function G: mĈ → mĈ, where mĈ := (ℤ\ ℤ) × Ĉ (see Figure 5).
2.5. The Realization Theorem
Shishikura proved in 6 the following theorem related with a Shishikura’s triple and its local model.
Theorem 2.1. Suppose that (T,d,F) is a Shishikura’s triple and has a model. Then (T,d,F) is realizable by a rational function f.
Summarizing the ideas exposed so far, in order to determinate the realization of a configuration of annuli, we need:
A configuration D of annuli.
Determinate the configuration of the configuration D.
Construct the abstract tree T(D) associated to D, as in Section 2.1.A.
Construct the narrowed abstract tree associated to T(D) taking into consideration the permutation given by the configuration.
Determinate the length of the edges of the narrowed abstract tree.
Determinate the local model of singular orbits on the end points of the narrowedabstract tree associated to T(D).
Remark 2.2. As a result of step 5 we obtain a linear system of n×n+1 equations, where one of the variables must be the length of the cyclic arc x n+1 . Thus, we will obtain that all the solutions will depend on x n+1 .
In the following section, we will give example of realizable configuration, keeping on the steps above.
3. Examples of realizable configurations for rational functions
In what follows we shall construct some examples of specific configurations of Herman rings realizable by a rational function by using the results from Section 2.
Example 3.1. Consider the configuration C 1 of the cyclic annuli given in Figure 6.
This configuration was proposed by Shishikura in 7, and it is the simplest one. The abstract tree associated to the configuration C 1 is given in Figure 7.
As we mention in Subsection 2.3, it is necessary to construct an associated narrowed tree (see Figure 8).
By 7, the configuration C 1 is realizable by a rational function.
Example 3.2. In the following example, consider the configuration C2 given in Figure 9.
The associated abstract tree to his configuration is given in Figure 10.
As we know, to construct the Shishikura’s tree T and define the function F for the configuration given we know that it is only necessary to determinate the length of the edges of T in term of the periodic arc x 5 , for which we will consider the following narrowed tree (see Figure 11).
In this case let us determine the lengths of the segments that form the abstract tree; in order to do it, consider the following system of equations:
Solving the above system of equations, we obtain that x 1 = x 2 = x 5 ,x 3 = 4x 5 ,x 4 = 5x 5 with x 5 > 0. Therefore, is possible to assign finite lengths to each segment and construct a finite topological tree.
Now, let us construct a local model for singular points in the given tree. In Table 1, we present the function g at each point of X, where the expression x → φ with x ∈ X, means that p β = φ, for the branch β at x containing the segment x. Considering that the degree of each one must be 2 for some functions given that DF = 2 for some segments, and that each function has a Siegel disk, and by using quasi-conformal surgery, we have a p-cycle of Herman rings.
Using the configuration C2, we can associate it to a narrowed tree with 10 symbols, say 0− ,0+ ,1− ,1+ ,...,5− ,5+, according to where the corresponding segment starts and finishes; these symbols are used in Table 1.
We recall two important facts: (i) α is a Diophantine number if
has infinitely many solutions in integers q for µ < v for some real number v and at most finitely many for µ < v; (ii) If the eigenvalue of a periodic orbit of rational function f is of the form e
2πα
with α a Diophantine number, then f has a p-cycle of Siegel discs, and therefore a cycle of Herman rings.
Example 3.3. Consider the configuration C3 of annuli in Figure 12.
Following the algorithm described in the Section 2.1.A, we obtain the tree associated to the configuration C3 (see Figure 13).
As 3.2, we can associate a narrowed tree associated to the abstract tree (see Figure 14).
From the above tree we can determinate the length of the segments solving the following system of equations associated to the narrowed tree:
The above system of equations has solution as follows:
As in the 3.2 and using the configuration C3, we can associate a narrowed tree with the symbols 0− ,0+ ,1− ,1+ ,...,15− ,15+ according to where the corresponding segment starts and finishes.With these symbols, we present the local model for singular orbits of the abstract tree associated to the configuration C3 (see Table 2).
From the Realization theorem, it implies that there exists a rational function g such that g has a cycle of Herman rings of period 15.
Example 3.4. We will show an example of a non realizable configuration in order to illustrate the importance of the local degree.
Consider the configuration C4 of a p-cycle of annuli given in Figure 15.
As the previous two examples, we need to determinate the lengths of the segments that form the tree, so, first we construct the abstract tree associated to the given configuration (see Figure 16).
We continue considering the narrowed tree associated to this abstract tree (see Figure 17).
The associated tree determines a linear system of equations given as follows:
The coefficients of the x i ’s correspond to the local degree of the desired function. The solution of the system of equations is: x 1 = 0, x 2 = 0, x 3 = 4x 15 , x 4 = −3x 15 , x 5 = 0, x 6 = x 15, x 7 = −5x 15 , x 8 = 4x 15, x9 = 0, x10 = 0, x11 = 4x15, x12 = 0, x13 = 0, x14 = 4x15, where x 15 denotes the length of the periodic arc. Thus, this configuration is non realizable, because there is no a continuous function on the abstract tree associated to the given configuration.
Now, we consider the following narrowed tree associated to the same configuration given in Figure 18, in which we change the local degree on some segments; in this case three, two and two on the segments x 1 ,x 2 and x 3 , respectively.
With these new conditions, we obtain that the system of equations has solution as follows:
where x 16 > 0 denotes the length of the periodic arc.
Therefore, from the Realization theorem, it implies that there exists a rational function g such that g realizes the configuration C 4.
