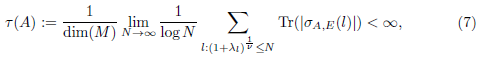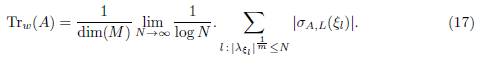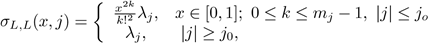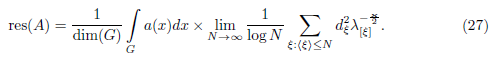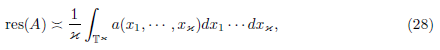Introduction
In this work, we classify the Dixmier traceability of some invariant operators on compact manifolds and we apply these results in order to study the Wodzicki residue of pseudodifferential operators. This work is a subsequent analysis to the program of M. Ruzhansky and J. Delgado on the classification of global operators in ideals contained in the algebra of bounded operators on Lebesgue spaces (see 16), (17), (18), (19), (20), (21). The topic has been of intense research in the last years not only for operators on compact manifolds, but also on non-compact manifolds and other spaces without a differentiable structure (see e.g. 1), (3), (4), (5), (6), (8), (9), (10), (11), (14), (15), (27), (24). The novelty of the announced results is that we use the matrix-valued global quantisation developed by Ruzhansky, Turunen, Tokmagambetov and Delgado, instead of the classical results on the subject based on the classical notion of the local symbol via localizations (see, e.g. Hörmander 26), as in 13), (23), (25), (33), (34 and references therein. We summarise our investigation in the following results:
- We provide necessary and sufficient conditions in order that global invariant pseudodifferential operators on a manifold with or without boundary belong to the Dixmier class L (1,∞) (L 2).
- We provide sufficient and necessary conditions in order to obtain Dixmier traceability for a type of pseudo-differential operators with global symbols in the Hörmander classes on compact Lie groups, and we express our results by using the representation theory of these groups. Also, we use Connes’ trace theorem in order to get formulae for the noncommutative residue of classical pseudo-differential operators on compact Lie groups.
- For a smooth compact manifold with or without boundary, we find criteria in terms of the global symbols in order that the corresponding operators belong to the Marcinkiewicz ideal L (p,∞) (L 2), 1 < p < ∞, as well as to the Dixmier ideal L (1,∞) (H) where H = L 2(M).
Our main result will be presented in Section 3. In Section 2 we provide some basics on the theory of pseudo-differential operators, the Wodzicki residue and the Dixmier trace. Finally, in Section 4 we provide some examples.
Preliminaries
In order to present our main results we recall some definitions (see Connes 13). Let H be a Hilbert space, L(H) be the algebra of bounded linear operators on H and K(H) be the ideal of compact operators on H. A compact operator A ∈ K(H) belongs to the Dixmier class L (1,∞) (H) if
where {s n (A)} denotes the sequence of singular values of A, which consists of the points in the spectrum of A∗A. The sequence s n (A) can be arranged in increasing order so that L (1,∞) (H) may be endowed with the norm
If A ∈ L (1,∞) (H), the functional kAkL(1 , ∞)(H) defines a norm. Some ideals, closely related to the Dixmier ideal, are Marcinkiewicz ideals L (p,∞) (H), defined by those bounded linear operators A on L2 satisfying the eigenvalue condition:
The main objects here are pseudo-differential operators, which we introduce as follows (16), (26), (31). A pseudo-differential operator A is an operator defined by the integral representation
where the function σ A (x,ξ) -called the symbol of A- satisfies estimates of the type (see Hörmander 26)
Here fˆ denotes the euclidean Fourier transform of the function f and m is the order of the pseudo-differential operator A. If we consider a compact manifold without boundary M of dimension κ, a pseudo-differential operator A on M can be defined by using the notion of local symbol; this means that for any local chart U, the operator A has the form
A pseudo-differential operator A is called classical, if σ
A
admits an asymptotic expansion  in such a way that each function σ
m−j
(x,ξ) is homogeneous in ξ of order m − j for ξ ≠ 0.. The set of classical pseudo-differential operators of order m is denoted by
in such a way that each function σ
m−j
(x,ξ) is homogeneous in ξ of order m − j for ξ ≠ 0.. The set of classical pseudo-differential operators of order m is denoted by  . For
. For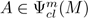 , and for x ∈ M,
, and for x ∈ M,
defines a local density which can be glued over M. In this case, the non-commutative residue of A is defined by the expression
The following fact is due to Connes, [13]: if  is a positive operator, then Tr
ω
(A) = res(A).
is a positive operator, then Tr
ω
(A) = res(A).
In the case of a manifold M with boundary, the typical algebra of pseudo-differential operators is known as the Boutet de Monvel algebra (BdM). This algebra is formed by matrix valued pseudo-differential operators associated with boundary value problems (see 2):
The noncommutative residue and the Dixmier trace for an operator P in BdM’s algebra have been studied e.g. in Fedosov 23 and Nest and Schrohe 28. In order to study the Dixmier trace and the non-commutative residue, we will use the notion of global pseudo-differential operator. If we consider a closed manifold M (i.e., a compact manifold without boundary) and H = L2(M), there exists a global Fourier analysis associated to every positive elliptic pseudo-differential operator E on M which gives for certain pseudo-differential operators A, -called E-invariants- , a discrete Fourier representation of the form
where
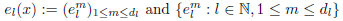 is a basis of L2 (M) consisting of eigenfunctions λl, l ∈ ℕ0, of E. The function σA,E is called the matrix valued symbol of A with respect to E. The quantisation procedure associating to every operator A acting in C∞(M) the matrix valued symbol σA,E was introduced by J. Delgado and M. Ruzhansky, 20. Also, If M = G is a compact Lie group and E = −LG is the positive Laplace-Beltrami operator on G, Ruzhansky and Turunen in 31 give a discrete representation to every pseudo-differential operator A acting on C∞ (G) in terms of the representation theory of the group G, in the following way:
is a basis of L2 (M) consisting of eigenfunctions λl, l ∈ ℕ0, of E. The function σA,E is called the matrix valued symbol of A with respect to E. The quantisation procedure associating to every operator A acting in C∞(M) the matrix valued symbol σA,E was introduced by J. Delgado and M. Ruzhansky, 20. Also, If M = G is a compact Lie group and E = −LG is the positive Laplace-Beltrami operator on G, Ruzhansky and Turunen in 31 give a discrete representation to every pseudo-differential operator A acting on C∞ (G) in terms of the representation theory of the group G, in the following way:
Here Ĝ denotes the unitary dual of G. Ruzhansky-Turunen’s calculus that gives a characterisation for the Hörmander clases
 on a compact Lie group G by using global symbols. In fact,
on a compact Lie group G by using global symbols. In fact,
 if and only if, its global symbol σA(x, ξ) as in (5) satisfies
if and only if, its global symbol σA(x, ξ) as in (5) satisfies
 where
where
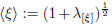 and
and
 is the spectrum of −LG, which can be enumerated by [ξ] ∈ Ĝ.
is the spectrum of −LG, which can be enumerated by [ξ] ∈ Ĝ.
Let us observe that if M = G is a compact Lie group and the operator
 is not invariant (this means that the global symbol σ
E
(x,ξ) depends of both variables, the spatial variable x ∈ G, and the Fourier variables [ξ] ∈ Gb), then in local coordinates, E-invariants operators A are E-multipliers, but they are not Fourier multipliers because in local coordinates their symbols are depending on the spatial variables.
is not invariant (this means that the global symbol σ
E
(x,ξ) depends of both variables, the spatial variable x ∈ G, and the Fourier variables [ξ] ∈ Gb), then in local coordinates, E-invariants operators A are E-multipliers, but they are not Fourier multipliers because in local coordinates their symbols are depending on the spatial variables.
In the formulation of our result for compact manifolds with boundary, we use the global quantization of pseudo-differential operators on compact manifolds with boundary due to J. Delgado, M. Ruzhansky and N. Tokmagambetov 30 which we briefly describe as follows. Let M be a compact manifold with boundary ∂M and let L be a pseudodifferential operator on M satisfying some boundary conditions on ∂M. We assume that L has discrete spectrum {λ ξ |ξ ∈ I}. If σ A,L : M × I → ℂ is a suitable function, the operator A associated with σ A can be written as
where 𝑓 := FL(f) denotes the L-Fourier transform of f introduced in 30. L-Fourier multipliers are bounded linear operators A : C L ∞(M) → C L ∞(M) satisfying FL(Af)(ξ) = σ A,L (ξ)FL(f)(ξ), for all f ∈ C L ∞(M), and for some function σ A,L : I → C depending only on the Fourier variables ξ ∈ I. In this case, σ A,L (ξ) is called the L-symbol of A.
The Dixmier Trace and the non-commutative residue for global pseudo-differential operators
In this section, we present our main results for global operators on compact manifolds. We start with the case of compact manifolds without boundary. Here, κ denotes the dimension of a fixed closed manifold.
Theorem 3.1. Let M be a κ-dimensional compact manifold without boundary and let
 be a positive elliptic pseudo-differential operator on M. If A : L2(M) → L2(M) is an E-invariant bounded operator with matrix-valued symbol (σ
A,E
(l))
l
, then we have that
be a positive elliptic pseudo-differential operator on M. If A : L2(M) → L2(M) is an E-invariant bounded operator with matrix-valued symbol (σ
A,E
(l))
l
, then we have that
- A is Dixmier traceable, i.e., A ∈ 𝓛 (1,∞) (L2(M)) if, and only if,
where σ A,E is as in (4). Moreover, if A is positive, τ(A) = Tr w (A).
- If A is an E-invariant operator, then A ∈ 𝓛 (p,∞) (L2(M)) if, and only if,
where 1 < p < ∞. In this case, ||A||𝓛 ( p, ∞ )(L 2 (M)) ≍ γ p (A).
- Let M = G be a compact Lie group and let Ĝ be the unitary dual of G. If we denote by σ A (x,ξ) the matrix valued symbol associated to A, then under the condition
the operator A is Dixmier measurable.
- If A ∈ Ψ− cl κ(G) is a classical and positive pseudo-differential operator and its symbol admits an asymptotic expansion in homogeneous components of the form:
then
The expression (11) in the preceding theorem gives a formula for the noncommutative residue of classical operators in terms of irreducible representations on G. We observe that our approach provide formulae for the noncommutative residue of operators on the torus, of a different way in relation with the recent work of Pietsch 29.
Now we present our result concerning to global operators on a manifold with boundary. With the notations above our result on the Dixmier traceability of operators on manifolds with boundary can be enunciated of the following way. We write I = {ξ l : l ∈ ℕ0}.
Theorem 3.2. Let M be a compact manifold with boundary ∂M. If A : L2(M) → L2(M) is a bounded Fourier multiplier, and L is a self-adjoint operator on L2(M), then we have the following assertions:
- A is Dixmier traceable if, and only if,
In this case, for A a positive operator, τ′(A) = Tr ω (A).
- Moreover, if L is an operator of order m satisfying the Weyl eigenvalue counting formula, that is,
then A is Dixmier traceable if, only if (cf. (12)),
In this case, for A a positive operator, τ′(A) = Tr ω (A).
- A ∈ L (p,∞) (L2(M)) if, and only if,
where 1 < p < ∞.
 . Moreover, if L satisfies (13), we have
. Moreover, if L satisfies (13), we have
On the other hand, let A = [P+,T]
t
be a column elliptic operator in the Boutet de Monvel algebra of order n. We assume the existence of L satisfying as in RuzhanskyTokmagambetov’s calculus. Any parametrix R of P
T
is Dixmier traceable and Tr
ω
(R) = res
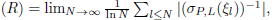 here (σ
P,L
(ξ
l
))
l∈ℕ0
denotes the global symbol of the operator P with respect to L. This residue’s formula is the same for all parametrix of A, R and independent of the boundary condition and independent of the average function ω. If in addition L satisfies the Weyl Eigenvalue Counting Formula, we also have
here (σ
P,L
(ξ
l
))
l∈ℕ0
denotes the global symbol of the operator P with respect to L. This residue’s formula is the same for all parametrix of A, R and independent of the boundary condition and independent of the average function ω. If in addition L satisfies the Weyl Eigenvalue Counting Formula, we also have
The proofs of these theorems and the corresponding analysis developed in this global setting can be found in Cardona and Del Corral 12. We refer the reader to Cardona, Del Corral and Kumar 7 where the Dixmier trace of discrete pseudo-differential operators has been investigated.
Examples
In this section we provide some examples in relation with our main results. First, we consider a Dixmier traceable Bessel potential associated to L. Also, we consider an example of a Dixmier traceable operator on the manifold with boundary M = [0,1]. Later, we consider the case of Bessel potential on SU(2) =∼ S3 and SU(3) respectively.
Example 4.1. Let M be a compact manifold with boundary ∂M and L as in the preceding sections. Let us consider the model operator L M self adjoint on L2(M). If we assume that −L is a positive operator of order ν, and some positive real number s1 satisfies
for all 0 < s ≤ s1 < s′ < ∞, then with the notations above the operator A := (I -L) - 𝑠1 𝑣 is Dixmier traceable on L2(M). For the proof, we combine that the global symbol of is given by
As consequence of (18) we have that
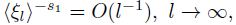 and
and
Hence, by Theorem 3.2 we obtain
Example 4.2. Consider M = [0,1] and the operator
 with the domain
with the domain
where a ≠ 0, b ≠ 0, and q ∈ C1[0,1], here
 Under the assumption that a + b + 0 1 𝑞 (x) dx=1 we have the inverse L-1 exists and is bounded from L2[0,1] to D(L). The operator L has a discrete spectrum which can be enumerated by λ
j
= 2πj − iln(−a/b) + α
j
, for j ∈ ℤ, where the sequence α
j
satisfies that for any ǫ > 0, Pj∈Z |α
j
|
1+ǫ
< ∞|. If| m
j
denotes the multiplicity of the eigenvalue λ
j
, then m
j
= 1 for sufficiently large j , and the system of eigenfunctions are given by
Under the assumption that a + b + 0 1 𝑞 (x) dx=1 we have the inverse L-1 exists and is bounded from L2[0,1] to D(L). The operator L has a discrete spectrum which can be enumerated by λ
j
= 2πj − iln(−a/b) + α
j
, for j ∈ ℤ, where the sequence α
j
satisfies that for any ǫ > 0, Pj∈Z |α
j
|
1+ǫ
< ∞|. If| m
j
denotes the multiplicity of the eigenvalue λ
j
, then m
j
= 1 for sufficiently large j , and the system of eigenfunctions are given by
Let j0 ∈ ℕ large enough so that m j = 1 for |j| ≥ j0. The global symbol σ L,L (x,j) of L with respect to L is given by
for some j0 ∈ N. It follows from the functional calculus that L−1 has a discrete spectrum given by λ−
j
1 with j ∈ Z. Since |λ
j
|=O(j) for j∈ ℤ, we have
 .
.
Therefore, L−1 is a pseudo-differential operator which lies in L (1,∞) (L2[0,1]) with symbol σ L − 1,L (ξ) = (σ L,L (ξ))−1, |ξ| ≥ j0, and
Example 4.3. Let us assume that A is a left-invariant operator on SU(2) =∼ S3. We recall that the unitary dual of SU(2) (see 31) can be identified as
There are explicit formulae for t l as function of the Euler angles in terms of the so-called Legendre-Jacobi polynomials, see 31. In this case, if A is Dixmier traceable with symbol σ([t l ]) ≡ σ(l), then
For example, if
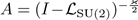 , is the Bessel potential of order −κ = −dimSU(2) = −3, then A is Dixmier traceable,
, is the Bessel potential of order −κ = −dimSU(2) = −3, then A is Dixmier traceable,
 and
and
A similar result can be obtained if we consider the operator
 , where Lsub := D1
2 + D2
2 is the sub-Laplacian on SO(3); here D1 and D2 are the derivatives in the corresponding variables to the Euler angles for SO(3) (see 31
), (
32]).
, where Lsub := D1
2 + D2
2 is the sub-Laplacian on SO(3); here D1 and D2 are the derivatives in the corresponding variables to the Euler angles for SO(3) (see 31
), (
32]).
Example 4.4. Let A be a left-invariant pseudo-differential operator Dixmier traceable on SU(3). The Lie group SU(3) has dimension 8 and 3 positive square roots α,β and ρ with the property
 . We define the weights
. We define the weights
With the notations above, the unitary dual of SU(3) can be identified with
The Dixmier trace of A, once denoted its full symbol by σ(λ) ≡ σ(λ(a,b)), is given by the expression
Since, the eigenvalues of the Laplacian LSU(3) on SU(3) are of the form
the symbol of the operator
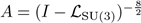 (which is Dixmier traceable) is given by
(which is Dixmier traceable) is given by
Hence,
Remark 4.5. Similar examples to the considered above can be obtained if we take, for example, every n-torus 𝕋n ≌ ℝ n /ℤ n or the compact Lie group SO(3) ≌ ℝℙ3, spheres 𝕊 n and arbitrary real and complex projective spaces.
Example 4.6. Let us assume that G is a compact Lie group of dimension κ, and let us define . A:=a(x)(LG) - x 2 We consider a(x) positive and smooth in order that A will be a positive operator. The global symbol of A is given by
and by using (11) we have that
In particular, for G = 𝕋x{, where 𝕋 ≡ [0, 1), d ξ = 1, and λ [ξ] = 1/4π2|ξ|2, ξ ∈ ℤ. In this case,
Consequently,
which is a well known fact (see e.g. Connes (13)).